太空城市构型比较

Comparison of Space City Configurations

摘要: 本文比较了太空城市的具有代表性的构型，包括刘慈欣圆杆、斯坦福圆环、伯纳尔球体、刘慈欣椭球、奥尼尔圆筒，分析了各种构型的受力特点，计算了在典型材料和尺寸下的应力大小。将太空城市的发展方针归纳为：“由近及远，由易到难，市场推动，效益为先，多方协作，共同发展”，并初步建议了从低轨到高轨，从地月系到日地系的逐步实施计划。同时开展旋转式太空太阳能发电站的工程应用，不但能够获取大量清洁能源，减少温室气体排放，而且也为地球“遮阳”，具有减缓全球气候变暖的作用。

Abstract: The typical configurations of space city are compared, including Liu Cixin rod, Stanford ring, Bernal sphere, Liu Cixin ellipsoid and O’Neill cylinder. The stress characteristics of each configuration are analyzed, and the stress magnitudes are calculated under typical materials and sizes. The development policy of space city is summarized as follows: “from near to far, from easy to difficult, market driven, benefit first, multi-party cooperation and common development”, and the gradual implementation plan is preliminarily proposed from low orbit to high orbit, from Earth-Moon system to solar-terrestrial system. At the same time, the engineering application of rotary space solar power station can not only obtain a lot of clean energy and reduce greenhouse gas emissions, but also “shade” the earth, which has the effect of slowing down global warming.

1. 引言

到太空中生活是人类的梦想，也是人类脱离摇篮时代的标志，在陆续实现将人送到太空，能够在太空中短期驻留之后，一个更加宏伟的目标就是建立太空城市，建设人类的第二个家园 [1] [2] [3]。1926年，人类航天技术的鼻祖康斯坦丁·齐奥尔科夫斯基就设想在将来的某一天，人类将在地球周围的宇宙空间建立居民点。他设想在太空中的失重环境下可以用自旋产生人工重力，通过人工控制的方法使室内的温度湿度适合于植物生长。他大胆预言：“选择收获量最大的农作物，在最佳的生长条件下，空间农场的每寸地方都可能充裕地养活宇宙移民”。

空间站是太空城市的先导，太空城市与空间站的主要区别在于，太空城市作为宇宙移民点，它应该是自给自足的，首先是食物的自给自足，而目前空间站上的生活品都是从地面上运去的。苏联在“礼炮”号和“和平”号空间站上，多次进行了植物栽培的长期实验，从培植小球藻等藻类实验到各种花卉、蔬菜和粮食作物，让这些植物在太空中经历了从播种到收获的全过程。太空农业的发展将成为太空城市正常运作的基本保障，也将为农业和生物科研活动开辟新的领域。

太空城市和空间站虽有不同，但从空间站发展到太空城市也是一个顺理成章的过程。太空城市的各种构型已经被科幻作家和物理学家不止一次地描述过，在很多影视作品中展现过。那么，这些太空城市是否具有现实意义？在工程建造难度上有多大？本文尝试收集整理了具有代表性的太空城市构型方案，并主要从其受力特点上进行了初步分析，讨论了每种构型在当前技术条件下的可行性，为现今蓬勃发展的太空探索和太空经济提供参考依据。

2. 空间站发展

空间站是一种在近地轨道长时间运行，可供多名航天员在其中生活工作和巡访的载人航天器，人类目前共出现了四代空间站 [4] [5]。第一代为实验飞行器性质，仅有一个对接口，意味着一次仅能对接一艘飞船，我国的天宫一号和二号也是类似功能。第二代为长期驻留空间站，此时已经带有两个对接口，可一次对接两艘飞船。此两代空间站都是单模块或称单一式空间站，具有硬件少、技术简单、不需要航天员出舱等优点，其缺点是不能扩展，因而容积小，效率低，也很难长期载人，它包括苏联的“礼炮”1~7号和美国的“天空实验室”。第三代空间站采用积木式的多模块组合构型，由多个舱段在轨道上对接而成，俄罗斯的“和平”号空间站即是此类构型。第四代空间站采用桁架挂舱式构型，即以长达数十米或数百米的组装式或展开式桁架为基本结构，将多个舱段和设备装在桁架上。

苏联于1971年4月19日发射升空的“礼炮1号”空间实验室，是世界首个空间站，自此之后又接连发射升空了6座“礼炮”系列空间站。1986年2月20日，苏联将“和平号”太空站送入近地轨道，组装后总质量达到129.7吨，成为人类最早建立的比较成功的空间站，后因部件老化且缺乏维修经费，最终于2001年3月23日坠入地球大气层。

现今运行的国际空间站为第四代空间站，总质量达到419吨，迄今已成功运行20余年 [6]。1998年11月20日，国际空间站第一个组件——“曙光”号功能货物舱发射升空。1998年12月4日，美国“奋进”号航天飞机携带美国为国际空间站建造的第一个组件——“团结”号节点舱升空，经过两天追赶，成功捕捉到“曙光”号功能货物舱并进行对接，标志着国际空间站开始建造。2000年7月26日，俄罗斯的“星辰”号服务舱与国际空间站联合体对接，成为宇航员生活和工作的主要场所。2000年10月31日，美俄3名宇航员成为国际空间站的首批长期住户。2004年1月美国居住舱在轨装配完毕后，国际空间站建成。

中国的空间站计划虽然启动较晚，但始终在稳步推进，并于2011年9月29日发射了我国第一个空间站“天宫一号”。即将建造的“天宫”空间站相当于第三代水平，总质量在100吨级，以三舱作为基本构型，预计在2022年完成，寿命十年，亦可通过维护延期 [7]。中国空间站总体构型和建造模式区别于“和平号”空间站和国际空间站，具有显著的中国特色和较为经济的建造方式，利用舱段交会对接和平面转位方式完成积木加局部桁架混合构型大型空间站的组装建造，在货运飞船、航天员和机械臂支持下，可完成类似国际空间站的复杂舱外建造和操作活动。

3. 刘慈欣圆杆

Figure 1. Liu Cixin rod space station

图1. 刘慈欣圆杆空间站

在前四代空间站中生活的宇航员处于无重力状态，而长期的太空飞行会削弱骨骼和肌肉，打乱钙代谢和正常的免疫系统。可以通过旋转产生的离心力来模拟重力，实验表明，当旋转半径小于100 m，转速高于3 rpm的情况下，人类会患运动病，而当旋转半径大于500 m，转速低于1 rpm的情况下，几乎所有人都能舒适生活。因此，提供较舒适模拟重力的空间站，可称之为第五代空间站，需要在结构尺寸上大大超过前四代空间站。

空间站进一步发展就是太空城市，太空城市比空间站更大型，人员驻留时间更长，生活条件更优，通常也被设计为可旋转的。太空城市的各种方案已被科幻小说家和工程师从多种角度提出，美国国家航空航天局(NASA)已重点考察的设计方案有伯纳尔球体、斯坦福圆环、奥尼尔圆筒等。

刘慈欣在其科幻小说《三体Ⅲ》中描述了一种简单的离心力构造结构 [8]：“比如一座叫资源一号的太空城，长度达到一百二十千米，直径却只有三千米，是一根细长的杆子，它并不是绕自己的长轴旋转，而是以中点为轴心翻着筋斗。这座太空城内部是分层的，不同层域的重力差异极大，只有少数几层适合居住，其余部分都是适合不同重力的工业区”。从模拟重力的效果看，不必要如书中描述的那样规模巨大，只需要细长的圆杆绕中点旋转就可以很方便地产生离心力，在圆杆末端挂载居住舱，就可以形成第五代空间站，成为太空城市的实验构型。

如图1所示，分析每根圆杆，设转动角速度为 $\omega$，圆杆截面积为S，密度为 $\rho$，则微元质量为 $\rho \cdot S\text{d}r$，产生离心力大小为 $\rho \cdot S\text{d}r\cdot {\omega }^{2}r$，圆杆一端旋转半径从0到r积分，得到总的离心力为

$F={\displaystyle {\int }_0^r\rho \cdot S\text{d}r}\cdot {\omega }^{2}r=\rho S{\omega }^2{\displaystyle {\int }_0^{r}r\text{d}r}=\frac{1}{2}\rho S{\omega }^2{r}^2$ (1)

于是轴心处的应力为

${\sigma }_0=F/S=\frac{1}{2}\rho {\omega }^2{r}^2$ (2)

可以看到，圆杆中因旋转产生的应力大小与杆的截面积无关，与材料的密度成正比，与旋转半径的平方成正比，与旋转圆频率的平方成正比。选择合适的旋转速度，可以使圆杆末端的加速度为重力加速度 $g={\omega }^{2}r=9.8\text{m}/{\text{s}}^{\text{2}}$，若最大旋转半径假设为1000 m，则 $\omega =\sqrt{9.8/1000}=0.099<0.105=2\pi /60=1\text{rpm}$，即低于1转/分，处于人体较舒适的范围。圆杆材料选取密度较小的铝材 $\rho =2.7\times {10}^3\text{kg}/{\text{m}}^{\text{3}}$，带入数值，计算得到圆杆旋转中心处最大应力为

${\sigma }_0=\frac{1}{2}\rho {\omega }^2{r}^2=\frac{1}{2}\times 2.7\times {10}^3\times 9.8\times 1000=13.23\times {10}^6\text{Pa}=13.23\text{MPa}$

假定在圆杆末端挂载的居住舱的质量为20 t，产生的离心力为 $m{\omega }^{2}r=mg=1.96\times {10}^5\text{N}$，圆杆直径取12 cm，则产生的附加应力为

${\sigma }_e=\frac{1.96\times {10}^5}{3.14\times {0.12}^2/4}\text{Pa}=17.34\text{MPa}$

总的应力为 $\sigma ={\sigma }_0+{\sigma }_e=30.57\text{MPa}$，可以看到，铝材很容易满足强度要求。需要的铝材质量为 $m=2.7\times {10}^3\times 3.14\times {0.12}^2/4\times 1000\text{kg}=30.52\times {10}^3\text{kg}=30.52\text{t}$。挂载居住舱后，并考虑到对称布置，总的单组质量为 $2\times \left(30.52+20\right)=101.04\text{t}$。即使增加太阳能电池板等其它设备，包含两个具有模拟重力居住舱的第五代空间站总质量并不大，可以在现有火箭发射能力下进行多次发射并组装完成。

圆杆组装时可通过螺纹旋接或焊接的方法，圆杆可在保持截面积相等的条件下尽量采用中空管道，以便于线缆通过。组装完毕后，在圆杆末端对称发动小型推进器，使整个结构旋转起来，速度足够就能模拟出所需重力。刘慈欣圆杆空间站还可以方便地扩大规模 [8]：“两个或几个杆状太空城可以自中部铰结在一起，形成十字形或星形的组合体”。如图1所示的空间站编组具有3组共6个舱室，入住航天员的数量很容易达到6人以上。

旋转离心力产生的模拟重力也可用于建造太空太阳能发电站，这时可以考虑采用较低的旋转速度，便于在较低的结构承载下达到更大的规模。受力的圆杆可以采用更高强的材料，比如碳纤维，这样使得旋转半径很容易达到10 km以上。在承力结构构成的旋转截面上布置太阳能电池板，利用离心力产生的张力保持结构形状，这样避免了为保持电池板展开状态所需的大量附属结构，以最少的构件达到同样的功用。从结构的尺寸来看，不管承力的圆杆采用何种材料，最后都可当作柔性的绳索，而电池板附着于上，构成一张紧密编织的网状电池板阵列，远看犹如一张圆圆的荷叶，在太空中漂浮并缓缓旋转。

假定这种旋转式的太空太阳能电站的旋转半径为1000 m，电池板的发电效率为25%，太阳常数采用1367 w/m²，可得最大发电功率 $P=3.14\times {1000}^2\times 1367\times 0.25\text{W}=1.07\times {10}^9\text{W}$，即得到百万千瓦级的太空太阳能电站。如果旋转半径为10 km，则发电站功率将达上亿千瓦，发电规模十分可观。这种太阳能电站的优点是需要的支撑结构十分简单，制造成本不高，主要的费用是火箭发射费用。如果发电组件采用太阳能薄膜电池，虽然发电效率差一些，但整体质量大大减小，发射费用将大幅下降，而整体结构如同旋转的手帕一样，仍然能够很好保持展开状态。如果将薄膜电池用反光薄膜替代，则可以将大量阳光简单反射回宇宙空间，达到为地球打伞“遮阳”的目的。

4. 斯坦福圆环

(a) (b)

Figure 2. Stanford ring space city. (a) Integral structure; (b) Interior landscape

图2. 斯坦福圆环太空城。(a) 整体构造；(b) 内部景观

将刘慈欣圆杆顶端的居住舱全部连接起来就自然形成了斯坦福圆环，这种构型主要得名于最早开展太空城市设计方案研究的斯坦福大学。刘慈欣书中也描写到 [8]：“从太平洋一号出来后，曹彬还带程心看了几座特异构型的太空城，其中距太平洋一号较近的是一座轮辐状城市，就是程心六十多年前曾经到过的地球太空电梯终端站的放大版。程心对太空城未全部建造成轮辐状一直不太理解，因为从工程学角度来看，轮辐状是天空城最理想的构型，建造它的技术难度要远低于整体外壳构型的太空城，建成后具有更高的强度和抗灾能力，而且便于扩建”。如图2所示为斯坦福圆环的整体构造和内部景观，是兼具良好受力条件和宽敞活动空间的太空城市构型。

连接斯坦福圆环辐心的拉杆或其它结构(如五角星形、六边形等)若主要作连接之用，可以不考虑受力，而主要的受力构件为圆环本身。设圆环的截面积为S，则离心力为

$\text{d}F=\rho \cdot Sr\text{d}\phi \cdot {\omega }^{2}r=\rho S{\omega }^{2}r\cdot r\text{d}\phi$ (3)

从离心力的方向看，与均匀内压力的方向一致，等效的内压力为 $p_0=\rho S{\omega }^{2}r$，从半个圆环处截断，考虑力的平衡，有

$2S\cdot {\sigma }_0=p_0\cdot 2r$

于是

${\sigma }_0=p_{0}r/S=\rho {\omega }^2{r}^2$ (4)

假设旋转半径为1000 m， ${\omega }^{2}r=9.8\text{m}/{\text{s}}^{\text{2}}$，材料为铝材 $\rho =2.7\times {10}^3\text{kg}/{\text{m}}^{\text{3}}$，带入数值有

${\sigma }_0=\rho {\omega }^2{r}^2=2.7\times {10}^3\times 9.8\times 1000=26.46\times {10}^6\text{Pa}=26.46\text{MPa}$

若圆环内有效载荷线质量密度为 ，则等效内压力为 $p_e=\bar{m}{\omega }^{2}r$，产生的附加应力为

${\sigma }_e=p_{e}r/S=\bar{m}{\omega }^2{r}^2/S$ (5)

可以看到，圆环的有效截面积越大，能承载的有效载荷也越大。假设线质量密度 $\bar{m}=2\times {10}^3\text{kg}/\text{m}$，有效截面积S = 1 m²，则 ${\sigma }_e=2\times {10}^3\times 9.8\times 1000/1=19.6\times {10}^6\text{Pa}=19.6\text{MPa}$，总的应力为 $\sigma ={\sigma }_0+{\sigma }_e=46.06\text{MPa}$，在可接受的范围内。若圆环截面直径为5 m，则壁厚为 $1/5\pi =0.064\text{m}=64\text{mm}$。有效载荷达到 $2\pi r\bar{m}=2\times 3.14\times 1000\times 2\times {10}^3\text{kg}=1.256\times {10}^4\text{t}$，可见承载量十分可观。斯坦福圆环在工程上的难度主要是太空中大型管道的可靠焊接，使之达到所需强度。在保持截面有效面积相同的情况下，截面可取其它形状，比如椭圆等，以便于内部空间的有效使用。

继续增加斯坦福圆环的有效截面面积，有效承载力将增大，如截面有效面积取为S = 100 m²，在保持应力相同的情况下，有效荷载线质量密度为 $\bar{m}=200\times {10}^3\text{kg}/\text{m}$，总承载质量超过百万吨。此时由于空间增大，必须考虑内部气压所产生的附加应力。若截面处圆的直径D = 160 m，则壁厚为 $100/160\pi =0.199\text{m}$。此时1个大气压0.1 MPa产生的纵向附加应力为 ${\sigma }_p^m=p\cdot \pi D^2/4/S=0.1\times 3.14\times {160}^2/4/100\text{MPa}=20.1\text{MPa}$，此时纵向总应力为 $\sigma ={\sigma }_0+{\sigma }_e+{\sigma }_p^m=66.16\text{MPa}$，仍然不大。同时由于气压作用存在与纵向应力垂直的环向附加应力为

${\sigma }_p^{\theta }=p\cdot D/2/t=0.1\times 160/2/0.199\text{MPa}=40.2\text{MPa}$

如果需要更大的空间，可以考虑将整个旋转空间都用材料包裹起来，这就形成了伯纳尔球体。

5. 伯纳尔球体

Figure 3. Bernal sphere space city

图3. 伯纳尔球体太空城

伯纳尔球体由物理学家伯纳尔在1929年首次提出，在刘慈欣所著书中也描写到 [8]：“他们首先去的是距亚洲一号最近的北美一号，那是一座纯球体形状的太空城。这种设计的最大优势在于，只需在球心有一个人造太阳即可使所有地区得到相同的光照。但球体构型的缺陷也很明显，主要是不同纬度地区的重力差异较大，赤道地区重力最大，随着纬度升高重力减小，两极地区处于失重状态。这样，在不同地区居住的人必须适应不同重力下的生活”。

如图3所示，伯纳尔球体在赤道处旋转半径最大，离心力也最大，若各纬度的应力自相平衡，可直接根据旋转半径得到离心力产生的应力：

${\sigma }_0=\rho {\omega }^2{\left(r\cos \phi \right)}^2=\rho {\omega }^2{r}^2{\cos }^2\phi$ (6)

最小处在两极为0，在 $\phi ={30}^{\circ }$ 时为 $0.75\rho {\omega }^2{r}^2$。最大处在赤道为 $\rho {\omega }^2{r}^2$，带入数值有

${\sigma }_0=2.7\times {10}^3\times 9.8\times 1000=26.46\text{MPa}$

球内气压假设为均匀的，切出半个圆球，根据力的平衡条件，有

$2\pi r\cdot t\cdot {\sigma }_p=\pi r^2\cdot p$

${\sigma }_p=\frac{r}{2t}p$ (7)

假设球壁厚为1 m，球半径为1000 m，代入有 ${\sigma }_p=1000/2/1\times 0.1=50\text{MPa}$。可以看到，此时气压产生的附加应力已超过离心力产生的应力。再考虑有效载荷的离心力产生的附加应力，若球体内有效载荷线密度为 $\bar{m}$，赤道处产生的附加应力最大，等效内压力为 $p_e=\bar{m}{\omega }^{2}r$，应力为

${\sigma }_e=p_{e}r/t=\bar{m}{\omega }^2{r}^2/t$ (8)

假定 $\bar{m}=2\times {10}^3\text{kg}/\text{m}$，有 ${\sigma }_e=2\times {10}^3\times 9.8\times 1000/1=19.6\times {10}^6\text{Pa}=19.6\text{MPa}$，总的应力 $\sigma ={\sigma }_0+{\sigma }_e+{\sigma }_p=26.46+19.6+50=96.06\text{MPa}$，仍控制在100 MPa以内。

由于球体沿赤道向两极旋转半径变小，离心力减小，同时方向与地面并不垂直，相当于有一定斜坡，如果斜坡超过某个数值就不适宜布置居住区，则可估计实际利用面积的大小。如图3所示，对某个纬度，此时旋转半径为 $r\cos \phi$，沿圆周的长度为 $2\pi r\cos \phi$，对应的倾斜长度为 $r\text{d}\phi$，于是扫过的面积为 $2\pi r\cos \phi \cdot r\text{d}\phi$，从赤道开始，积分到某个纬度有

$S={\displaystyle {\int }_0^{\phi }2\pi r\cos \phi \cdot r\text{d}\phi }=2\pi r^2{\displaystyle {\int }_0^{\phi }\cos \phi \text{d}\phi }=2\pi r^2\sin \phi$ (9)

当 $\phi ={90}^{\circ }$ 时，就是上半球面面积 $2\pi r^2$，整个球体的面积为 $4\pi r^2$。如果只居住到纬度30˚，则利用面积为 $2\cdot 2\pi r^2\sin {30}^{\circ }=2\pi r^2$，恰好为整个球面的一半，带入数值为 $2\times 3.14\times {1000}^2{\text{m}}^2=6.28{\text{km}}^2$，按人口密度8000人/km²计算，可居住约5万人。

6. 刘慈欣椭球

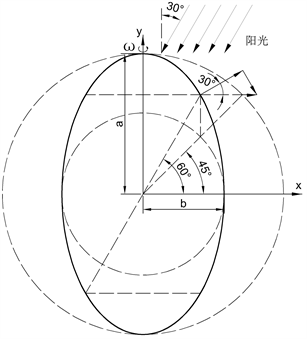
Figure 4. Liu Cixin ellipsoid space city

图4. 刘慈欣椭球太空城

伯纳尔球体虽然提供了很大的居住空间，但在两极附近区域由于模拟重力方向与地面不垂直而形成斜坡，使得宜居区所占比例不够大，这时可以考虑其它形状，比如椭球体，以扩大宜居区面积比例。在刘慈欣所著《三体Ⅲ》中描述到 [8]：“在球形或椭球形城市构型中，在重力方向上赤道是最低处，城市的水体自然集中于此，形成一个环绕城市中部的水环，成为城市的一条波光粼粼的腰带”。在旋转中轴线上为失重区，可作为其它用途 [8]：“在欧洲四号的长轴线上建设了所有太空城中最高或最长的建筑物，它长四十千米，连接椭球体的南北极，本身就形成了一根长轴。由于内部处于失重状态，主要用作太空港和商业娱乐区”。

如图4所示，椭圆绕长轴旋转可形成椭球体，椭圆的参数方程设为

$\{\begin{array}{l}x=b\cos \phi \\ y=a\sin \phi \end{array}$ (10)

其中 $a>b$，微分可得 $\text{d}x=-b\sin \phi \text{d}\phi$， $\text{d}y=a\cos \phi \text{d}\phi$，过椭圆上某点的切线斜率为

$\frac{\text{d}y}{\text{d}x}=\frac{a\cos \phi \text{d}\phi }{-b\sin \phi \text{d}\phi }=-\frac{a}{b}\text{ctg}\phi$ (11)

而法线斜率为

$-\frac{\text{d}x}{\text{d}y}=-\frac{-b\sin \phi \text{d}\phi }{a\cos \phi \text{d}\phi }=\frac{b}{a}\text{tg}\phi$ (12)

仍取法线为30˚方向，则有

$\frac{b}{a}\text{tg}\phi =\text{tg}{30}^{\circ }=\frac{\sqrt{3}}{3}$

$\text{tg}\phi =\frac{a}{b}\cdot \frac{\sqrt{3}}{3}$ (13)

若取 $a/b=\sqrt{3}$，则 $\text{tg}\phi =1$， $\phi ={45}^{\circ }$，此时实际仰角为 ${\text{tg}}^{-1}\left(y/x\right)={\text{tg}}^{-1}\sqrt{3}={60}^{\circ }$。若取 $a/b=3$，则 $\text{tg}\phi =\sqrt{3}$， $\phi ={60}^{\circ }$，此时实际仰角为 ${\text{tg}}^{-1}\left(y/x\right)={\text{tg}}^{-1}3\sqrt{3}={79.1}^{\circ }$。

根据对称性，椭圆的周长为在第一象限部分的4倍

$L=4{\displaystyle {\int }_0^{\pi /2}\sqrt{\text{d}{x}^2+\text{d}{y}^2}}=4{\displaystyle {\int }_0^{\pi /2}\sqrt{b^2{\sin }^2\phi +a^2{\cos }^2\phi }\text{d}\phi }=4{\displaystyle {\int }_0^{\pi /2}\sqrt{a^2-\left(a^2-b^2\right){\sin }^2\phi }\text{d}\phi }$

令偏心率 $e=\sqrt{\frac{a^2-b^2}{a^2}}=\sqrt{1-{\left(\frac{b}{a}\right)}^2}$，则

$L=4a{\displaystyle {\int }_0^{\pi /2}\sqrt{1-\frac{a^2-b^2}{a^2}{\sin }^2\phi }\text{d}\phi }=4a{\displaystyle {\int }_0^{\pi /2}\sqrt{1-e^2{\sin }^2\phi }\text{d}\phi }$ (14)

此为椭圆积分，虽不能用初等函数表示，但有精度很高的拉马努金近似公式

$L=\pi \left(a+b\right)\left(1+\frac{3h}{10+\sqrt{4-3h}}\right)$， $h=\frac{{\left(a-b\right)}^2}{{\left(a+b\right)}^2}$ (15)

取 $b=1000\text{m}$， $a=\sqrt{3}b=1732\text{m}$，计算得 $h=7-4\sqrt{3}$， $L=8737.6\text{m}$。假设椭球体内气压为均匀，切出半个长轴椭球，根据力的平衡条件，有：

$Lt\cdot {\sigma }_p=\pi ab\cdot p$

${\sigma }_p=\frac{\pi ab}{Lt}p$ (16)

假设壁厚为1 m，代入有 ${\sigma }_p=3.14\times 1732\times 1000/8737.6/1\times 0.1=62.24\text{MPa}$。

在赤道处旋转半径最大，离心力也最大，如果不考虑变形协调，可能产生的最大应力为 ${\sigma }_0=\rho {\omega }^2{r}^2=2.7\times {10}^3\times 9.8\times 1000\text{Pa}=26.46\text{MPa}$。可以看到，此时气压产生的附加应力已超过自身结构离心力产生的应力。再考虑有效载荷的离心力产生的附加应力，若球体内有效载荷线质量密度为 $\bar{m}$，赤道处产生的附加应力最大，等效内压力为 $p_e=\bar{m}{\omega }^{2}r$，产生应力为

${\sigma }_e=p_{e}r/t=\bar{m}{\omega }^2{r}^2/t$ (17)

假定有效载荷线质量密度 $\bar{m}=2\times {10}^3\text{kg}/\text{m}$，则有效载荷的离心力产生的附加应力为 ${\sigma }_e=2\times {10}^3\times 9.8\times 1000/1=19.6\times {10}^6\text{Pa}=19.6\text{MPa}$。总应力 $\sigma ={\sigma }_0+{\sigma }_e+{\sigma }_p=26.46+19.6+62.24=108.3\text{MPa}$，工程上仍较为可行。

现在计算适宜居住的面积，如图4所示，对旋转得到的某个环带，环带周长为 $2\pi b\cos \phi$，在环带某点处的切线方向长度为 $\sqrt{\text{d}{x}^2+\text{d}{y}^2}=\sqrt{b^2{\sin }^2\phi +a^2{\cos }^2\phi }\text{d}\phi$，环带的面积为两者之积，于是对上半部分椭球体表面从0积分到 $\phi$ 为

$S={\displaystyle {\int }_0^{\phi }2\pi b\cos \phi \cdot \sqrt{b^2{\sin }^2\phi +a^2{\cos }^2\phi }\text{d}\phi }=2\pi ab{\displaystyle {\int }_0^{\phi }\sqrt{\frac{b^2}{a^2}{\sin }^2\phi +{\cos }^2\phi }\text{d}\left(\sin \phi \right)}$

令 $\gamma =\sin \phi$，有

$S=2\pi ab{\displaystyle {\int }_0^{\sin \phi }\sqrt{\frac{b^2}{a^2}{\gamma }^2+\left(1-{\gamma }^2\right)}\text{d}\gamma }=2\pi ab{\displaystyle {\int }_0^{\sin \phi }\sqrt{1-\frac{a^2-b^2}{a^2}{\gamma }^2}\text{d}\gamma }$

再令 $\sqrt{\frac{a^2-b^2}{a^2}}\gamma =e\gamma =\sin \beta$，则 $\text{d}\gamma =\frac{1}{e}\cos \beta \text{d}\beta$，代入有

$S=2\pi ab{\displaystyle {\int }_0^{\arcsin \left(e\sin \phi \right)}\frac{1}{e}{\cos }^2\beta \text{d}\beta }=\frac{2\pi ab}{e}{\left[\frac{1}{2}\beta +\frac{1}{4}\sin 2\beta \right]}_0^{\arcsin \left(e\sin \phi \right)}$

$S=\frac{\pi ab}{e}\left(\arcsin \left(e\sin \phi \right)+e\sin \phi \sqrt{1-e^2{\sin }^2\phi }\right)$ (18)

若令 $\phi ={90}^{\circ }$，就得到长轴椭球上半表面积为

$S=\frac{\pi ab}{e}\left(\arcsin \left(e\right)+e\sqrt{1-e^2}\right)=\pi b^2+\pi ab\cdot \arcsin \left(e\right)/e$ (19)

在偏心率 $e=0$ 时椭球体退化为球体， $a=b=r$，利用极限定义可得 $S=2\pi r^2$，此即上半球体表面积。

取 $b=1000\text{m}$， $a=\sqrt{3}b=1732\text{m}$， $\phi ={45}^{\circ }$，代入有 $e=\sqrt{2/3}$， $e\sin \phi =\sqrt{1/3}$，整个椭球体表面积为 $2\left(3.14+3.14\times 3/\sqrt{2}\times \arcsin \sqrt{2/3}\right)\times {1000}^2{\text{m}}^2=19.01{\text{km}}^{\text{2}}$，坡度较缓的宜居面积为 $2\left(3.14+3.14\times 3/\sqrt{2}\times \arcsin \sqrt{1/3}\right)\times {1000}^2{\text{m}}^2=14.48{\text{km}}^{\text{2}}$，利用率为76%。按人口密度8000人/km²计算，可居住 $14.48\times 8000=115840$ 人，即超过11万人。

取 $b=1000\text{m}$， $a=3b=3000\text{m}$， $\phi ={60}^{\circ }$，代入有 $e=\sqrt{8/9}$， $e\sin \phi =\sqrt{2/3}$，整个椭球体表面积为 $2\left(3.14+3.14\times 9/2\sqrt{2}\times \arcsin \sqrt{8/9}\right)\times {1000}^2=30.88{\text{km}}^{\text{2}}$，宜居面积为 $2\left(3.14\times 3/2+3.14\times 9/2\sqrt{2}\times \arcsin \sqrt{2/3}\right)\times {1000}^2{\text{m}}^2=28.51{\text{km}}^2$，利用率为92%。按人口密度8000人/km²计算，可居住 $28.51\times 8000=228080$ 人，即超过22万人。

可以看到，将伯纳尔球体变为绕长轴旋转的椭球体后，便于利用的较平坦居住区面积比例增大，如果希望居住区完全平坦，太空城市则可采用奥尼尔圆筒构型。

7. 奥尼尔圆筒

美国科学家奥尼尔在他的《高边疆：人类的太空城》(《The High Frontier: Human Colonies in Space》)一书中，提出了一个名为“三号岛”的太空城，并设想未来人们可在这种太空城中居住生活。在刘慈欣所著书中也描述到 [8]：“亚洲一号是掩体工程最早建设的太空城之一，呈规则的圆筒形，旋转产生的离心力模拟重力”，“这是太空城的最北端，是一个直径八千米的大圆盘，在地面看不出圆形来，只能看到大地从两侧升起。圆盘顶端的高度与珠峰差不多，连接着太空城的另一面。有许多辐条从环绕圆盘的地面汇聚到四千米高的圆心，每根辐条都是一条电梯轨道，圆心就是太空城的出入口”。

Figure 5. O’Neill cylinder space city

图5. 奥尼尔圆筒太空城

奥尼尔圆筒构型太空城以圆筒中轴为旋转轴，通过旋转产生重力。圆筒的内壁正好是城市的地面，因此生活在太空城的人，站在此地面上，跟站在地球的地面上的感觉是大同小异的。只是在太空城里，头顶都正好对着圆筒的中轴线，因此有一个特别景致——人可以透过天空中的浮云，能隐隐约约看到头顶上的“地面”，那里的山峰、树木、房屋和行人都是头朝下倒立着的 [1]。

整个太空城是一个巨大的密闭生态循环系统，可以解决空气和水的循环供应问题。辐射防护则可由居室的金属结构外壳解决。科学家设想将圆筒壁分成六大区域：三个居住区和三个天窗区，使大圆筒内有充足的阳光。太空城有大型超市、医院、图书馆、电影院、音乐厅、体育馆等，还有设备完善的科学站和天文台。自动化农场提供新鲜的蔬菜、水果、鸡、鸭、鱼、肉、蛋和奶，农产品自给自足完全没有问题。太空城还拥有工厂，可将月球和小行星上运来的矿石进行冶炼和加工，即可生产钢材、水泥、火箭燃料和化工产品等。圆筒的中轴部分没有离心力，这里的工厂正好可以利用失重的特殊条件生产出在地球上无法生产的东西，比如提炼非常纯净的大块晶体，制造轻得能浮在水面的泡沫钢等等。

如图5所示，奥尼尔圆筒两端封闭部分可用半球封闭，受力分析类似于伯纳尔球体。圆筒其余部分的受力分析较为简单，此时内部气压、自身的离心力、有效荷载的离心力都产生相同的效果。截取单位长度圆筒，再从中部剖开，考虑半个圆筒的受力平衡条件，有

$2t\cdot \sigma =2r\cdot \left(p_0+\rho t{\omega }^{2}r+\bar{m}{\omega }^{2}r\right)$

于是

$\sigma =\frac{r}{t}{p}_0+\rho {\omega }^2{r}^2+\frac{r}{t}\bar{m}{\omega }^{2}r$ (20)

假设圆筒半径为1000 m，圆筒壁厚1 m，代入得到内部气压导致的应力 ${\sigma }_p=0.1\times 1000/1=100.0\text{MPa}$。材料取为铝材 $\rho =2.7\times {10}^3\text{kg}/{\text{m}}^{\text{3}}$，自身离心力产生的应力为 ${\sigma }_0=2.7\times {10}^3\times 9.8\times 1000\text{Pa}=26.46\times {10}^6\text{Pa}=26.46\text{MPa}$。假定有效荷载密度为 $\bar{m}=2\times {10}^3\text{kg}/\text{m}$，有效荷载离心力产生的应力为 ${\sigma }_e=2\times {10}^3\times 9.8\times 1000/1\text{Pa}=19.6\times {10}^6\text{Pa}=19.6\text{MPa}$。总的应力 $\sigma ={\sigma }_0+{\sigma }_e+{\sigma }_p=26.46+19.6+100.0=146.06\text{MPa}$，应力较大，其中气压导致的应力占很大比例。如同地球上大气压力随高程增加会逐渐减小，太空城内空气也有相同效应，考虑此效应后总的应力会有所减小。如果外壳采用铝材安全性不够，也可采用铝锂合金等更好的材料，还可用碳纤维进行加强，使整体结构满足要求。

奥尼尔圆筒太空城市的居住区是平坦的，在长度上可以延伸很长，比如有10 km，则可利用的居住面积为 $S=2\pi rl=2\times 3.14\times 1000\times 10000{\text{m}}^2=62.8{\text{km}}^2$，按人口密度8000人/km²计算，可居住 $62.8\times 8000=502400$ 人，即约50万人。

8. 太空城市建造

从以上对各种太空城市构型的初步计算分析可以看出，随着空间站发展到第五代，将具备模拟重力的功能，能够提供人体长期健康生活的基本条件。刘慈欣圆杆构型通过在旋转圆杆的末端挂载居住舱，可达到第五代空间站的要求，是空间站和太空城市之间的过渡形式。旋转圆杆构型的空间站总质量不大，还可通过多个圆杆组合扩大规模，因此较易实现。斯坦福圆环是一种居住空间较大的太空城市构型，在工程材料受力上也容易满足要求，但建造所需的材料多于刘慈欣圆杆，在运载火箭发射费用大量下降的情况下可逐步实施，以满足太空旅游的需要。伯纳尔球体太空城市则有更广阔的空间，可在内部形成完整的生态系统，但这对大型封闭金属外壳的太空建造提出了挑战，同时由于离心力的斜坡影响，使得适宜居住的区域利用率不高，这时可以考虑采用刘慈欣椭球构型，能较为完美地解决这一问题。奥尼尔圆筒构型太空城市的居住区域完全平坦，宜居区域的利用率最大，但在结构受力条件上比不上其它构型，需要更高强度的材料才能满足要求。综合来看，太空城市宜由小到大逐步发展，其中斯坦福圆环在工程难度和生活质量上处于适中程度，但如果期望更舒适的太空生活，还需考虑空间更大的太空城市构型。

太空城市本身封闭的生态系统和积极的生态循环可以明显降低对地球的依赖性，以便尽量维持自给自足的状态。运作太空城市需要解决的核心技术除了人工重力技术外，还必须建立可靠的生命支持系统，发展太空农业，此外，太空城市处在真空之中，既要处理好来自太阳的热量，也要处理好城市内部所产生的热量，即需要热量平衡系统。它还需要有足够的保护层，以防止太空陨石及尘埃等意外袭击，即防灾修复系统。种种问题的存在都需要逐一克服，才能较为安全有效地实际运作太空城市。

Figure 6. Combination configuration of space city

图6. 太空城组合构型

太空城市的各个构型还可组合在一起，增大居住规模，提高安全性和可靠性。如刘慈欣书中描述 [8]：“每座太空城都带有一个或多个标准接口，可以相互对接组合，组合后的城市居民的流动空间成倍扩大，有着更好的世界感，对社会经济的发展具有重大意义。连通后的大气和生态系统成为一个整体，运行状态更为稳定。目前的城市对接方式一般为同轴对接，这样对接后可以同轴旋转，保持对接前的重力环境不变”。如图6所示为椭球体和圆环体的组合，其中椭球体可用作主要的生活区，空间开阔，生活质量高，而圆环体用作太空港口和工作区，也可在生活区出现危险时作为临时避难所。

太空城市建造时，首先要解决的是选址问题，拉格朗日计算发现，在太空中有一些特殊的点，在该点处物体受到各个天体的引力处于相互平衡状态，因此不会轻易离开自己的位置，具有永久性。太空城市应该优先选择建在太空中的这些特殊点上，这样无需进行轨道维持或只需很少的维持能量 [9] [10]。如图7所示，太阳和地球之间的拉格朗日L1点(距地球约150万千米)，地月系统的L1、L4、L5点等都是较为理想的地点，其中L4和L5点稳定性最好，基本不用考虑轨道维持的问题。

Figure 7. Sketch map of Lagrange points

图7. 拉格朗日点示意图

由于日地和地月系统中特殊的拉格朗日点并不多，而且距离地球较远，为建造和运行方便考虑，初期的太空城市还是需要尽量靠近地球。但近地轨道上运行的飞行器，即便大气非常稀薄也会使它慢慢减速而坠落，因此需要经常启动推进器加速来维持轨道 [11]。为降低发射质量，减少燃料消耗，较为理想的加速方法是采用霍尔推进器等电推装置，另外还可考虑基于太阳光压的轨道维持方案，即对太空城市的旋转状态进行调整，使之除绕自身主轴旋转外，相对于太阳也可进行缓慢旋转，从而面向太阳逆光运动时，减少光照垂直截面，光压减少，而背向太阳顺光运动时，增大光照垂直截面，光压增大，两相抵消后可获取一定的加速动能。此方案的优点是减少燃料消耗，即使加速效果微弱，但在大气特别稀薄的高轨道还是有一定作用，缺点是不能充分利用太阳能电池板的发电能力，可考虑在发电能力充裕的情况下优先采用。

远离地球的大型太空城市所需材料如果都从地球运送代价较大，从月球上取材更加合算。科学家发现月球岩石中含有丰富的铝、铁、钛、硅、氧等元素，修建太空城市的建筑材料大部分可以从月球找到。月球的引力只有地球的六分之一，在月球上发射火箭比从地球上发射能够增加百倍以上的有效载荷，效费比很高。因此如果先开发月球，利用月球上的资源冶炼、加工成铝材、玻璃等各种建筑材料构件，然后将构件用电磁发射装置抛射到太空城市所在轨道上，经过太空建造作业逐渐装配形成完整构型，最后通过小型推进器使太空城旋转起来产生离心力，并在内部空间填充可供人类呼吸的混合气体，就可使太空城市满足基本的入住条件。

由于太空技术的提高和成熟需要较长的时间，不能急于求成，在发展过程中还需要十分重视经济性，使产生的效益能够覆盖技术开发费用，这样步伐虽慢但更为坚实。探索和利用外层空间的外空活动本身即具有鲜明的跨越国界的国际性，中国应当在“人类命运共同体”视角下的外层空间国际合作理念的指引下，除了在空间站建设领域的国际合作中积极作为，在太空城市建设中也必须通过开展国际合作方才能够充分地实现自身和彼此之间基于对外层空间的探索和利用所应取得的利益 [12]。综合考虑，可将人类建造太空城市的较为可行的发展方针归纳为：“由近及远，由易到难，市场推动，效益为先，多方协作，共同发展”。考虑技术难度，尝试将太空城市的建造过程分为以下步骤：

1) 在低轨道建设第五代空间站，测试模拟重力的实际效果并不断完善，探索空间站旋转启停技术和与之配套的停靠补给技术，积累人类在其中较长期生活的健康保持技术。

2) 在中轨道建设小型斯坦福圆环太空城市，完善太空焊接组装施工技术，开发太空旅游观光等商业价值。可在中高轨道建造多个旋转展开的中小型太阳能薄膜发电站，并将清洁能源输送回地球。

3) 在高轨道建设大型斯坦福圆环太空城市，探索基于太阳光压的轨道维持技术，拓展人类生存空间，并将之作为火箭燃料补给的停靠点，打造为深空探测前哨，不断发展太空农业和太空医疗等功能。

4) 建设月球生产和生活基地，开发月球各类资源，冶炼生产构筑太空城市的建筑材料，建立高效电磁推进装置以节省运送费用，不断积累人类长期驻留地外空间的各项技术。

5) 利用月球基地，在地月拉格朗日L4、L5点建设大型太空城市，可作为重要的天文观测基地和太空生产基地。采用积极的生态循环方法，不断完善太空城市封闭的生态系统维持技术。

6) 在日地拉格朗日L1点建设可容纳上百万人口的太空城市群，可作为探测金星的优良基地。建造巨型太阳能薄膜发电站，可在获取清洁能源的同时为地球打伞“遮阳”，以减缓地球气候变暖。

9. 结语

建设太空城市具有两个明显的价值，一是发展太空技术，二是拓展人类空间。在建造太空城市的同时，开展太空太阳能发电站的工程应用，可获取大量清洁能源，为太空城市供能，多余的电能也可转换为微波形式发送回地球，以替代大量燃烧化石能源的火电厂，减少二氧化碳和污染气体排放，为减缓地球气候变暖发挥作用。利用此种方法还可以尝试改变金星气候，即围绕金星布置众多太阳能薄膜电池或反光板，施行另类“戴森球”计划，阻挡太阳辐射，为金星降温，希有朝一日将金星改造为宜居星球。

外层空间于世界各国均具有显著的经济价值和战略意义，关系到全人类的共同命运。从空间站发展到太空城市，将不断提高人类在太空生活的长久性、舒适性，并逐渐做到自给自足的状态。从模拟重力的第五代空间站，到工程难度适中的斯坦福圆环，再到生活空间更加广阔的伯纳尔球体、刘慈欣椭球、奥尼尔圆筒，这些太空城市构型在现今技术条件下并没有不可逾越的困难，可逐步加以实施。同时随着太空城市工程建设规模的扩大，更加迫切需要廉价高效的太空运输手段来提高建造计划的可行性和经济性。可以预见，随着太空城市的逐步建设，太空技术必将飞速发展，人类也必将走出地球“摇篮”，实现在太空中惬意生活的梦想，并不断向更广阔的宇宙空间迈进。