基于ARIMA和BP神经网络的供应链需求预测模型及其对比分析

Supply Chain Demand Forecasting Model Based on ARIMA and BP Neural Network and Its Comparative Analysis

摘要: 提升整个供应链效益首要解决的任务是牛鞭效应，而提高预测精准度可以有效的抑制牛鞭效应。基于此在深入分析ARIMA模型和BP神经网络特性的基础上，以某商城办公用品的数据为例对需求量进行预测，选取绝对百分比误差MAPE、均方根误差RMSE和平均绝对误差MAE作为模型检验指标，比较相对误差衡量两种预测模型。构建有较高预测精度的模型，为企业应对市场需求变化提供重要的理论依据。

Abstract: The primary task to be solved to improve the efficiency of the entire supply chain is the bullwhip effect, and improving the accuracy of prediction can effectively suppress the bullwhip effect. Therefore, based on the in-depth analysis of the ARIMA model and the BP neural network characteristics, this paper takes the data of a certain mall office supplies as an example to predict the demand, and selects the absolute percentage error MAPE, the root mean square error RMSE and the average absolute error MAE as the model test indexes that compare the relative errors to measure the two forecasting models. Constructing a model with higher prediction accuracy provides an important theoretical basis for enterprises to respond to changes in market demand.

1. 引言

在供应链管理中，精准预测商品的短期需求量至关重要，不仅可以帮助企业制定合理的补货计划和库存决策以降低企业的库存成本，还可以使供应链和企业的运作效率得到改善。在面对复杂多变的市场时，传统的时序预测己经难以满足生产计划的需要。

Forrester率先在案例研究中发现牛鞭效应：以“订单”形式传递需求的过程中，上游节点无法准确地把握现实需求 [1]。研究发现在供应链模型下的牛鞭效应在企业中普遍存在，其中，订单决策是影响牛鞭效应的重要部分，由订单决策方法和需求量预测两个部分组成。Kenneth提出应用多阶段的ARIMA供应链，将此模型用于库存和订单的预测 [2]。国内外很多专家学者采用当前热门的神经网络方法在供应链领域去研究预测模型 [3] [4] [5] [6]。Min等人运用考虑季节性和趋势性的多层前馈神经网络进行预测，并根据MAPE、RMSE等指标与ARIMA进行了对比 [7]。雷可为等构建ARIMA和BP模型对游客量预测 [8]。此外，也有学者将ARIMA和BP网络组合构建预测模型应用于不同领域 [9] [10]。

以往企业常用一些传统时序预测方法，但是在实际应用中表现往往表现出其预测精度的有限性。本文对某商城办公用品2015年1月到2018年12月需求量的历史数据进行数据分析对比，并应用ARIMA和BP建立需求模型。试图发现较为准确的需求量预测模型，并希望该模型能够对未来短期的需求量有一定的预测能力。数据来源于UCI公开数据集，本文基于Python平台编写ARIMA模型和BP神经网络模型的脚本代码。

2. 基于ARIMA模型的需求预测模型构建

2.1. ARIMA模型概述

在ARIMA模型建立的过程中，首先需对所选取的数据进行自相关及偏自相关检验，判断所选取的数据是否平稳；若不平稳，则需对数据作相应地平稳化变换，即确定差分次数d；最后，确定p及q的值，进行ARIMA模型的建立。在建立了ARIMA模型后，为了保证所建立的模型是有效的，还需对模型的拟合优度进行检验。构建的ARIMA模型越有效拟合效果表现的越好。其中，ARIMA模型的通用表达式为：

$X_t={\phi }_1{X}_{t-1}+{\phi }_2{X}_{t-2}+\cdots +{\phi }_p{X}_{t-p}+{\epsilon }_t-{\theta }_1{\epsilon }_{t-1}-{\theta }_2{\epsilon }_{t-2}-\cdots -{\theta }_q{\epsilon }_{t-q}$ (1)

式中， ${\phi }_{\text{1}},{\phi }_2,\cdots ,{\phi }_p$ 是自回归系数，p是自回归阶数， $\left\{{\epsilon }_t\right\}$ 是白燥声序列，d为差分阶数， ${\theta }_{\text{1}},{\theta }_2,\cdots ,{\theta }_q$ 是移动平均系数，q是移动平均阶次，通常该模型拟写为ARIMA (p, d, q)。

下面给出ARIMA模型的详细建模步骤：

Step1：数据准备：将原始数据处理后绘制时序图，并根据图形检查数据的变化趋势；

Step2：异常值检查与清理：计算原始数据取值的上下限，对超过上限或低于下限的异常值，采用取临近两个数据均值的方式进行平滑化处理；

Step3：对数据的平稳性进行检验：对非平稳的数据做差分处理并确定d的取值；

Step4：模型拟合：确定p和q的取值，完成模型的拟合；

Step5：模型预测：确定预测周期，运用Step4拟合的模型进行预测。

2.2. 构建ARIMA模型

在前述分析的基础上，本文选用ARIMA模型进行对我国某商城2015年1月到2018年12月每月的办公用品需求量构建模型。

由图1可知，购买办公用品的人数总的趋势是逐渐增加，但有的年份也存在局部下降，但时序数据增长的幅度大小不一，这说明该序列缺乏平稳性，存在趋势性，此情况可能会影响模型预测的精准性。因此，需将其数据作相应地平稳化处理。此外，时间序列图像在每一年都有规律波动，这说明办公用品需求量的时间序列可能存在季节性因素。

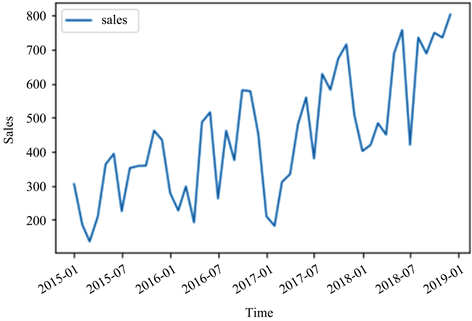
Figure 1. Curve: demand of office supplies from 2015 to 2018

图1. 2015~2018年办公用品需求量曲线

2.2.1. 需求数据的平稳化

在实际解决供应链预测问题时，由于ARIMA模型要求时序数据是稳定的，或者通过差分化后是稳定的。因此将经过平稳化处理的时序数据传入模型进行拟合，最后在多个拟合结果中根据相关判定指标与参数估计显著性确定最优的预测模型。

由图2、图3可以看出，原序列经过一阶差分处理后已经基本趋于平稳状态，且一阶与二阶的差分差别很小，所以取ARIMA模型参数d = 1。

2.2.2. ARIMA模型p和q的确定

利用图4、图5对参数进行预判。

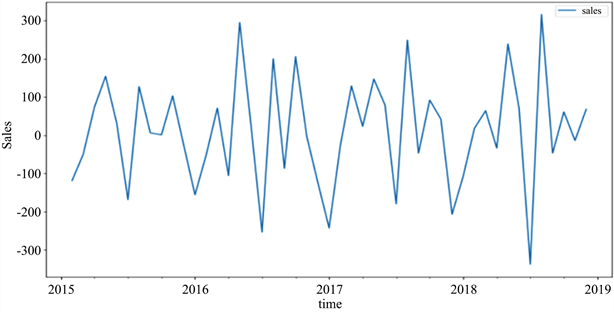
Figure 2. Sequence diagram: first-order difference

图2. 一阶差分的时序图

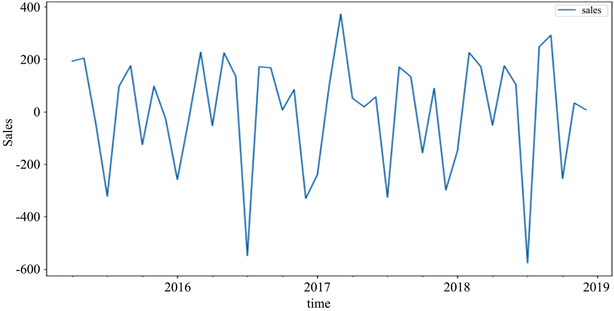
Figure 3. Sequence diagram: second order difference

图3. 二阶差分的时序图

Figure 4. Diagram: autocorrelation

图4. 自相关图

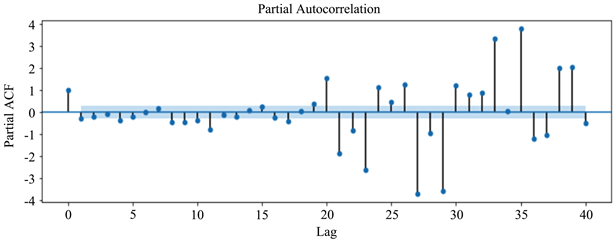
Figure 5. Diagram: partial autocorrelation

图5. 偏自相关图

由图4可知，自相关函数一阶是显著的，即一阶之后截尾，所以可以先设定ARIMA模型中的参数q为0、1。同样，通过图5可看出拖尾的情况，因此p值可取1到4。经过排列组合，我们可以得到8种可能的ARIMA模型。在所有的ARIMA模型中，ARIMA (4, 1, 1)模型的MAPE最小，表现了最好的预测性能，因此最终选定的预测模型为ARIMA (4, 1, 1)。

2.3. ARIMA (4, 1, 1)预测模型的应用

利用ARIMA (4, 1, 1)模型对2015年至2018年4年的办公用品需求量数据进行拟合，然后进行部分年份的预测。从图6中可以看出，个别的点存在误差较大的情况，但在总体趋势上，橘色的预测曲线大致拟合蓝色的真实曲线。对于短期的时间序列，从2017年3月1日至2018年12月1日的橘色预测曲线可以看出，ARIMA模型的预测能力较好。

为了量化模型预测的准确性，我们可以计算指标以作出评判。但由于办公用品需求量会受到客观因素的影响，以及模型自身的限制因素，只能进行短期的预测。在短期预测中，该模型具有一定的可信度，可以此模型为基础，对未来的需求量作出预测。

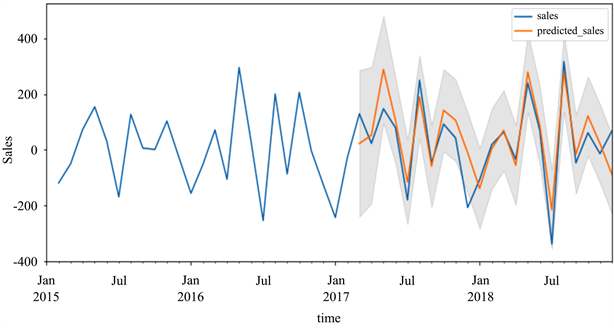
Figure 6. Curve: t results of ARIMA forecast

图6. ARIMA预测结果曲线

3. 基于BP神经网络的需求预测模型构建

3.1. BP神经网络的原理

BP网络层由输入、隐含和输出层构成。将误差进行反向传播对输入的样本进行训练，根据误差不断调整权重直到误差达到初始目标设定值便停止迭代。

BP神经网络是一种多层次回馈的神经网络，主要特征是通过输出后的数据与实际值的误差来调节各层之间的权值，调整后的数据再反馈回上一层继续估计误差并调整，从而每一层之间反向传播，得到所有层的误差估计。从数学上看，神经网络是一个复合函数，已经证明，只要激活函数选择适当，神经元数量足够多，就可以实现对任意函数形式的逼近。有监督的BP神经网络模型的算法学习过程如下：

Step 1：初始化，确定神经元的转换函数(Sigmoid函数)。设定误差函数E、学习率L、计算精度值 $\epsilon$ 和最大学习次数M，并选择初始权值 $W_0$ ；

Step 2：计算网络输出 $y_k$ ；

Step 3：用式 $E=\frac{\text{1}}{\text{2}}{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\left(y{}_k-y_k^{\ast }\right)}^2}$ 计算误差函数E，如果 $E<\epsilon$，转至Step 5，否则转Step 4；

Step 4：由式 $\Delta w_{jk}\left(N\right)=-L_{w_{jk}}\frac{\partial E}{\partial w_{jk}\left(N\right)}+{\alpha }_{w_{jk}}\Delta w_{jk}\left(N-1\right)$ 和 $\Delta w_{ij}\left(N\right)=-L\frac{\partial E}{\partial w_{ij}\left(N\right)}+{\alpha }_{w_{ij}}\Delta w_{ij}\left(N-1\right)$ 调整权值，转至Step 2；

Step 5：存储最优值 $W^{\text{*}}$，算法结束。

3.2. 构建BP神经网络模型

3.2.1. 归一化处理

将数据进行归一化处理至区间[0, 1]之间，公式如下为：

${\bar{x}}_i=\frac{x_i-x_{\min }}{x_{\max }-x_{\min }}$ (2)

3.2.2. 网络参数设置及训练算法

根据对影响因素的分析，给定训练集，确定输入节点和输出节点以及数据维度。本文选用三层的网络架构。为了得到较为理想的预测模型，将神经元个数、学习率、激励函数作为控制变量进行模型训练并试预测后得到相对较优的网络参数值。在梯度下降的思想中，学习率决定着算法每一步迭代中的更新步长，若学习率较小，则需要较高的迭代次数才能达到收敛；若学习率较大，则容易产生振荡，甚至会出现无法收敛的情况。神经网络中常用的激活函数为Logistic、Tanh、Relu等函数。

为了确定模型的最优参数，需要反复训练此网络。将最大迭代次数设为10,000次，学习率设为0.001，中间层的传递函数选用Relu函数，以此使网络的学习周期大幅度缩短。BP算法基本思想是：初始化权值和阈值，通过层间前向传播计算出输出值，网络训练得到最优权值使误差达到最小。

3.3. 预测分析

选取2017年至2018年的数据检验模型的训练情况，预测结果如图7所示。

在图7中，蓝色、橘色曲线分别表示真实、预测需求数据曲线。从数据的拟合情况可以看出，大部分预测数据和真实数据相差不大，有些月份预测误差较大，但整体预测效果较好，在几个跳跃点上模型也能够及时作出正确的判断，预测曲线能够很好地拟合原数据曲线。

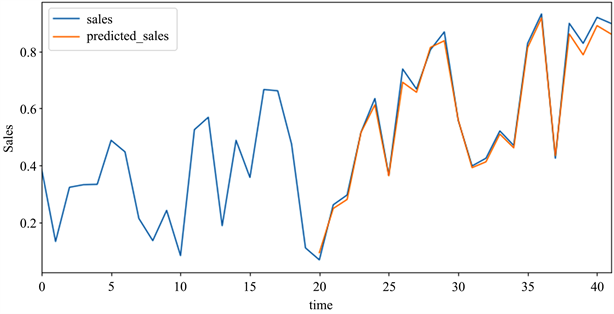
Figure 7. Curve: t results of BP forecast

图7. BP预测结果曲线

4. 基于ARIMA模型与BP神经网络预测结果的比较分析

验证ARIMA与BP模型的有效性。虽然它们很有用，而且被广泛用于比较同一数据集上的不同方法，但在这里，表达相对于我们试图预测的时间序列的大小的误差会更有用。为了量化对比结果，对两个模型采用以下三个评判指标进行对比分析。各指标数据结果见表1。评判指标的计算公式如下：

$\text{RMSE}=\sqrt{\frac{\text{1}}{n}{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\left({\hat{y}}_i-y_i\right)}^2}}$ (3)

$\text{MAPE}=\frac{\text{100\%}}{n}{\displaystyle \underset{i=1}{\overset{n}{\sum }}\left|\frac{{\hat{y}}_i-y_i}{y_i}\right|}$ (4)

$\text{MAE}=\frac{\text{1}}{n}{\displaystyle \underset{i=1}{\overset{n}{\sum }}\left|{\hat{y}}_i-y_i\right|}$ (5)

式中，RMSE表示均方根误差，MAPE表示平均绝对百分比误差，MAE表示平均绝对误差，范围均为 $\left[0,+\infty \right)$，当预测值与真实值的差值越接近0，表示模型越完美。

Table 1. Comparison of error results between ARIMA model and BP network model

表1. ARIMA模型和BP网络模型误差结果对比

通过表1中看出，ARIMA预测模型虽然也可以较好地对时序数据进行预测，但拟合效果不如BP神经网络模型表现出色。

表2详细罗列了模型的相对误差值。对比表格数据可知，BP模型在预测精度方面的表现力和稳定性上总体稍优于ARIMA模型，因此BP模型是较为有效的。

Table 2. Comparison of prediction results between ARIMA model and BP network model

表2. ARIMA模型和BP网络模型预测结果对比

本文主要使用ARIMA模型描述历史数据的线性关系，BP神经网络模拟数据的非线性规律，可以很好的处理非线性问题和不确定性问题。本文在供应链领域中主要分析了需求波动，提升需求量的预测精度从而达到对牛鞭效应的抑制。

5. 结论

综上所述，供应链效益受到复杂市场环境的影响，牛鞭效应带来的负面影响日益严重，逐步增加了节点企业的运行成本和经营风险。长久以来，无数学者对于牛鞭效应的抑制措施进行深入的研究，本文经过对国内外大量文献的阅读，确定了提高需求预测精度来降低牛鞭效应的研究方向。本文基于供应链牛鞭效应与需求预测的相互关系，构建需求模型以得到更准确的预测，从而抑制牛鞭效应对供应链的影响。

本文主要分析了某商城办公用品的需求量，对需求数据的特征和规律进行统计分析，构建ARIMA和BP模型，以达到改善预测效果的作用。建立此模型对需求量进行更准确的预测，缓解牛鞭效应，减少库存积压，优化生产计划，提高企业和所在供应链整体的运作效率。

基金项目

国家自然科学基金资助项目(61863022)；中国博士后科学基金资助项目(2017M623276)。

参考文献

NOTES

^*通讯作者。