一维空间中极大值原理的条件研究

Research on the Condition of Maximum Principle in One-Dimensional Space

摘要: 本文通过改变条件函数c(t)的取值范围，得到了条件函数 时极大值原理不成立的反例。同时，通过举反例的方法得到了条件函数c(t)≥0不是极大值原理成立的必要条件。

Abstract: In this paper, by changing the value range of the conditional function c(t), counterexamples are obtained that the maximum value principle does not hold when the conditional function is . At the same time, the conditional function c(t)≥0 is not a necessary condition for the maximum principle to be established through counterexamples.

1. 引言

极大值原理是苏联学者Л.С.庞特里亚金在20世纪50年代中期提出来的。它的提出将经典变分学推进到了现代变分学，是对分析力学中古典变分法的推广。极大值原理可以解决工程领域中的一些最优控制问题，成为现代控制理论的重要基石，见参考文献 [1]。因此，研究极大值原理有着极其重要的理论价值和现实意义。随着研究的深入，一系列极大值原理应运而生，比如：极值曲线的极大值原理、抛物型方程的极大值原理、椭圆型方程的极大值原理、关于泛函的极大值原理、拟线性抛物型方程的极大值原理，见参考文献 [2] - [7]。首先，根据参考文献 [8]，给出一维空间中的极大值定理。

定理 [8] 假设 $u\left(t\right)\in C^2\left(0,1\right)\cap C\left[0,1\right]$，且满足在 $\left(0,1\right)$ 上 $-u^{″}\left(t\right)+c\left(t\right)u\left(t\right)\le 0$，其中在 $\left(0,1\right)$ 上 $c\left(t\right)\ge 0$。如果 $u\left(t\right)$ 在 $\left[0,1\right]$ 上有非负的最大值，那么 $u\left(t\right)$ 不在 $\left(0,1\right)$ 内取到该最大值。

本篇论文针对一维空间中极大值原理的条件函数进行了讨论，研究了其条件函数 $c\left(t\right)\ge 0$ 的重要性。

2. 条件函数 $c\left(t\right)<0$ 时极大值原理不成立的反例

令 $c\left(t\right)=\frac{-6}{t-t^2\text{+}1}$， $t\in \left(0,1\right)$，满足在定义域范围内 $c\left(t\right)<0$。如图1所示。

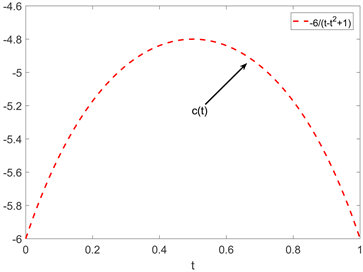
Figure 1. Image of conditional function $c\left(t\right)<0$

图1. 条件函数 $c\left(t\right)<0$ 的图像

令

$u\left(t\right)=t-t^2\text{+}1$, $t\in \left[0,1\right]$,

其中 $u\left(t\right)\in C^2\left(0,1\right)\cap C\left[0,1\right]$ 且在 $\left(0,1\right)$ 内有非负的最大值， $u^{″}\left(t\right)=-2$。如图2所示。

故

$-u^{″}\left(t\right)+c\left(t\right)u\left(t\right)=2+\left(-\frac{6}{t-t^2+1}\right)\times \left(t-t^2+1\right)=2-6=-4<0$, $t\in \left(0,1\right)$,

满足在 $\left(0,1\right)$ 内 $-u^{″}\left(t\right)+c\left(t\right)u\left(t\right)\le 0$。

Figure 2. Image 1 where the function $u\left(t\right)$ does not meet the condition in the problem setting

图2. 函数 $u\left(t\right)$ 不满足题设条件的图像1

会发现，只要令 $c\left(t\right)=\frac{-k}{t-t^2+1}\left(k\ge 2\right)$， $t\in \left(0,1\right)$，对于 $u\left(t\right)=t-t^2+1$， $t\in \left[0,1\right]$，尽管在 $\left(0,1\right)$ 内都满足

$-u^{″}\left(t\right)+c\left(t\right)u\left(t\right)\le 0$,

但是 $u\left(t\right)$ 在 $\left(0,1\right)$ 内有非负的最大值。

因此，条件函数 $c\left(t\right)\ge 0$ 对于极大值原理的成立是非常重要的。

3. 条件函数 $c\left(t\right)$ 变号时极大值原理不成立的反例

令 $c\left(t\right)={\left(10-20t\right)}^2-22$， $t\in \left(0,1\right)$，满足在定义域范围内 $c\left(t\right)$ 正负不定。如图3所示。

Figure 3. The image when the conditional function $c\left(t\right)$ changes sign

图3. 条件函数 $c\left(t\right)$ 变号的图像

令

$u\left(t\right)={\text{e}}^{-10{\left(t-0.5\right)}^2}$, $t\in \left[0,1\right]$,

其中 $u\left(t\right)\in C^2\left(0,1\right)\cap C\left[0,1\right]$ 且在 $\left(0,1\right)$ 内有非负的最大值，

$u^{″}\left(t\right)=-20{\text{e}}^{-10{\left(t-0.5\right)}^2}+{\left(10-20t\right)}^2{\text{e}}^{-10{\left(t-0.5\right)}^2}$.

如图4所示。

Figure 4. Image 2 where the function $u\left(t\right)$ does not meet the condition in the problem setting

图4. 函数 $u\left(t\right)$ 不满足题设条件的图像2

故

$\begin{array}{c}-u^{″}\left(t\right)+c\left(t\right)u\left(t\right)=20{\text{e}}^{-10{\left(t-0.5\right)}^2}-{\left(10-20t\right)}^2{\text{e}}^{-10{\left(t-0.5\right)}^2}+\left[{\left(10-20t\right)}^2-22\right]{\text{e}}^{-10{\left(t-0.5\right)}^2}\\ =-2{\text{e}}^{-10{\left(t-0.5\right)}^2}\end{array}$, $t\in \left(0,1\right)$,

满足在 $\left(0,1\right)$ 内 $-u^{″}\left(t\right)+c\left(t\right)u\left(t\right)\le 0$。如图5所示。

Figure 5. Image where the function $-u^{″}\left(t\right)+c\left(t\right)u\left(t\right)$ meets the condition in the problem setting

图5. $-u^{″}\left(t\right)+c\left(t\right)u\left(t\right)$ 满足题设条件的图像

因此，条件函数 $c\left(t\right)\ge 0$ 对于极大值原理的成立是非常重要的。

4. 条件函数 $c\left(t\right)\ge 0$ 不是极大值原理成立的必要条件

1) 令 $u\left(t\right)=t^2-t+0.1$， $t\in \left[0,1\right]$，其中 $u^{″}\left(t\right)=2$，可知 $u\left(t\right)\in C^2\left(0,1\right)\cap C\left[0,1\right]$ 且在 $\left(0,1\right)$ 内没有非负的最大值。如图6所示。

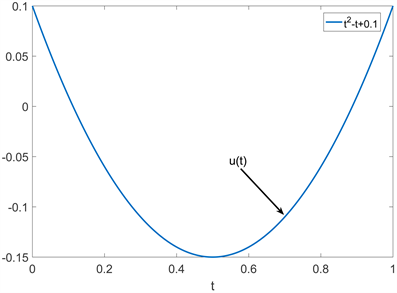
Figure 6. The function $u\left(t\right)$ satisfies the image 1 of the problem setting condition

图6. 函数 $u\left(t\right)$ 满足题设条件的图像1

令 $c\left(t\right)=-\sin t-1$， $t\in \left(0,1\right)$，其中在定义域范围内 $c\left(t\right)<0$。所以

$-u^{″}\left(t\right)+c\left(t\right)u\left(t\right)=-2-\left(\sin t+1\right)\times \left(t^2-t+0.1\right)$, $t\in \left(0,1\right)$,

满足在 $\left(0,1\right)$ 内 $-u^{″}\left(t\right)+c\left(t\right)u\left(t\right)\le 0$。如图7所示。

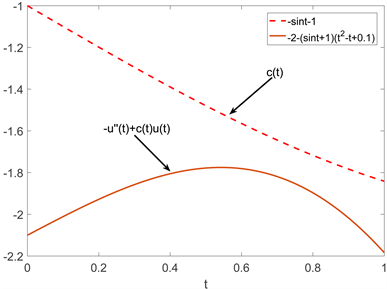
Figure 7. The image where the maximum principle holds when the conditional function $c\left(t\right)<0$

图7. 条件函数 $c\left(t\right)<0$ 时极大值原理成立的图像

2) 令 $u\left(t\right)=t^2-t+0.5$， $t\in \left[0,1\right]$，其中 $u^{″}\left(t\right)=2$，可知 $u\left(t\right)\in C^2\left(0,1\right)\cap C\left[0,1\right]$ 且在 $\left(0,1\right)$ 内没有非负的最大值。如图8所示。

令 $c\left(t\right)=\sin t-0.5$， $t\in \left(0,1\right)$，其中在定义域范围内 $c\left(t\right)$ 变号。所以

$-u^{″}\left(t\right)+c\left(t\right)u\left(t\right)=-2+\left(\sin t-0.5\right)\times \left(t^2-t+0.5\right)$, $t\in \left(0,1\right)$,

满足在 $\left(0,1\right)$ 内 $-u^{″}\left(t\right)+c\left(t\right)u\left(t\right)\le 0$。如图9所示。

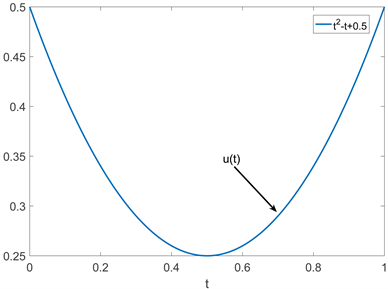
Figure 8. The function $u\left(t\right)$ satisfies the image 2 of the problem setting condition

图8. 3函数 $u\left(t\right)$ 满足题设条件的图像2

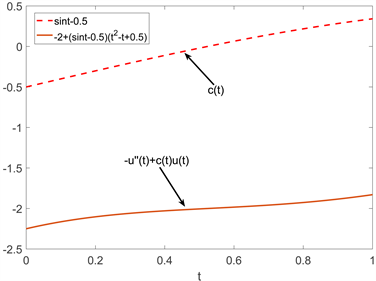
Figure 9. The image where the maximum principle holds when the conditional function $c\left(t\right)$ changes sign

图9. 条件函数 $c\left(t\right)$ 变号时极大值原理成立的图像

综上所述，当条件函数 $c\left(t\right)<0$ 和 $c\left(t\right)$ 变号时都可以找到相应的 $u\left(t\right)$ 满足题设条件，故条件函数 $c\left(t\right)\ge 0$ 是上述极大值原理成立的充分不必要条件。