基于多复函的各向异性板弹性力学解法

Solution Method of Elastic Mechanics for Anisotropic Plate Based on Multiple Complex Functions

摘要: 各向异性板是复合材料基本结构形式，其应力边值问题的弹性力学解法成为工程结构受力分析的理论基础。本文运用多复变函数论的概念，选择典型的边界受力各向异性板，建立求解弹性力学问题的基本方程与多复函方法。作者通过引入多复变量和坐标代换方法推导出各向异性板的应力场。本文思路与解法有助于改进复合材料力学的基础理论和研究方法。

Abstract: The anisotropic plate is the basic construction shape of composite materials. The solution method of elastic mechanics for its stress boundary problems must become the basis of loading analysis to engineering structures. By using the concept of multiple complex variable functions and selecting the typical anisotropic plate to be loaded on the local edge, the basic equations and multiple com-plex function methods have been established for solving the elastic mechanical problems. By means of introducing the multiple complex variables and the coordinate replace method, the stress fields of the anisotropic plate have been determined. The train of thought and the solution method in this paper may be an aid to improve the basic theory and research method in the composite mechanics.

1. 引言

弹性力学是与工程建设领域关系密切的一门基础学科，在理工科教育及学术研究方面已形成完整的经典理论，并被广泛应用到土木建筑工程、机械工程、船舶工程、航空航天工程等各个设计项目中。近百年来，弹性理论不断扩展，出现了许多新的研究领域，例如断裂力学、结构力学、计算力学和复合材料力学等学科，尤其是先进复合材料的工程应用日益扩张，复合材料弹性力学的理论发展显得更加重要。多复变函数论是一种更广泛的函数论概念，将常用单变量复变函数理论推广到多维空间复变量的广义复变函数方法，史济怀，陆启铿等专著中有详细介绍 [1] [2]。多复变函数论在高等数学中得到应用，例如关于整函数导数定理的证明，以及将多复变函数论应用于不定积分计算 [3] [4]。毫无疑问，多复函理论的应用前景与研究潜力非常深厚宽阔，必将成为不同工程领域基础研究与创新应用的强有力工具。自上世纪开始，科学家们运用复变函数法求解偏微分方程方面做出了巨大贡献，并将复变函数理论不断拓展，开创了泛复变函数研究的新理论与工程应用方法 [5] [6]。随着复合材料工程日益兴盛，推广复变函数法解决各向异性材料弹性力学问题就必然成为一种有效途径。高健，刘官厅运用广义复变函数方法求解复合材料板弹性问题，本文作者也用泛复函方法解决复合材料平面应力问题 [7] [8] [9]。近年来利用广义复变函数法求解正交异性材料典型边值问题方面已取得坚实的理论基础，且基本理论和工程应用的研究热潮方兴未艾。因此，为推动各向异性材料弹性力学问题的深入研究，作者认为有必要对多复变函数方法进行广泛探索，使其求解方法和相关理论更加完善，并在解决复合材料弹性力学问题上获得新进展。

2. 复合材料弹性力学的基本理论

为了叙述清楚，先将有关基础理论列举出来。众所周知，解决弹性力学问题基本方法主要从三个方面考虑：静力学、几何学和物理学。通常都用应力分量作为基本变量求解平面应力边值问题，忽略体力时的静力平衡微分方程为：

$\frac{\partial {\sigma }_x}{\partial x}+\frac{\partial {\tau }_{xy}}{\partial y}=0,\frac{\partial {\tau }_{xy}}{\partial x}+\frac{\partial {\sigma }_y}{\partial y}=0$ (1)

这组线性齐次微分方程式的通解可用实变函数 $F\left(x,y\right)$ 表示，即：

${\sigma }_x=\frac{{\partial }^{2}F}{\partial y^2}=F_{yy},{\sigma }_y=\frac{{\partial }^{2}F}{\partial x^2}=F_{xx},{\tau }_{xy}=-\frac{{\partial }^{2}F}{\partial x\partial y}=-F_{xy}$ (2)

复合材料层合板的宏观力学性能可视为均匀各向异性材料特征，其板内的弹性力学分析可按照平面应力状态处理。为了便于复合材料力学分析，主要考虑面内形变的物理学性能。在平面应力状态下的各向异性材料本构关系为：

$\begin{array}{l}{\epsilon }_x=a_{11}{\sigma }_x+a_{12}{\sigma }_y+a_{16}{\tau }_{xy}\\ {\epsilon }_y=a_{12}{\sigma }_x+a_{22}{\sigma }_y+a_{26}{\tau }_{xy}\\ {\gamma }_{xy}=a_{16}{\sigma }_x+a_{26}{\sigma }_y+a_{66}{\tau }_{xy}\end{array}\}$ (3)

式中各个常数 $a_{ij}$ 为参考坐标系 $\left(x,y\right)$ 下各向异性材料的柔度系数。平面内的三个应变分量必须满足相容条件，也就是应变协调方程：

$\frac{{\partial }^2{\epsilon }_x}{\partial y^2}+\frac{{\partial }^2{\epsilon }_y}{\partial x^2}=\frac{{\partial }^2{\gamma }_{xy}}{\partial x\partial y}$ (4)

将应力分量表达式(2)代入物理方程(3)，再将所得的应变分量代入协调方程(4)，由此可导出求解一般复合材料平面应力问题的基本方程为：

$\frac{{\partial }^{4}F}{\partial y^4}+A_1\frac{{\partial }^{4}F}{\partial x\partial y^3}+A_2\frac{{\partial }^{4}F}{\partial x^2\partial y^2}+A_3\frac{{\partial }^{4}F}{\partial x^3\partial y}+A_4\frac{{\partial }^{4}F}{\partial x^4}=0$ (5)

式中： $A_1=-\frac{2a_{16}}{a_{11}},A_2=\frac{a_{66}+2a_{12}}{a_{11}},A_3=-\frac{2a_{26}}{a_{11}},A_4=\frac{a_{22}}{a_{11}}$

基本方程(5)是一个常系数齐次线性偏微分方程，应力函数F为实函数，可根据给定边值问题选择合适的函数类型，以便求得具体问题的解答。以上列出的基本方程作者也在参考文献 [8] [9] 中提到，本文重新写出的原因就是便于后面叙述清晰，更利于读者容易理解检验有关公式的正确性。

在弹性力学书籍中，按应力法求解平面应力边值问题是必须掌握的基础内容，也是十分经典的解题方法。由于各向异性材料力学的弹性常数多，基本方程中包含较多弹性常数，使得寻找一般解答较为困难。然而，利用复变函数方法仍可以解决一些典型的复合材料平面应力边值问题，以下举例说明。考虑一块各向异性材料的平板，在部分边界受到压缩的分布载荷作用，如图1所示(图中符号p表示单位面积力，其量纲与应力相同)。

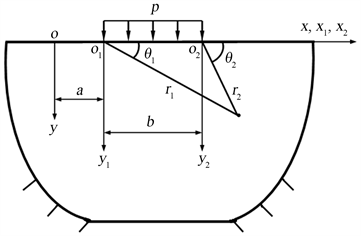
Figure 1. Partial edge of anisotropic plate subjected to distributing pressure and coordinates

图1. 各向异性板局部边界受分布力作用及坐标系

按照弹性力学一般边界受力分析方法，可根据平面应力边值问题的给定条件和基本方程推导解答。本例求解过程中主要考虑直边界的面力状态，由图1可见需要满足的应力边界条件为：

$\begin{array}{l}{\sigma }_y=-p,{\tau }_{xy}=0\left(a<x<a+b,y=0\right)\\ {\sigma }_y=0,{\tau }_{xy}=0\left(x<a,y=0\right)\\ {\sigma }_y=0,{\tau }_{xy}=0\left(x>a+b,y=0\right)\end{array}\}$ (6)

3. 各向异性板应力边值问题的多复变函数解法

在解决弹性力学平面边值问题时，利用复变函数及其坐标变换法能够求得一些典型的结果，若采用实函数求解就十分困难。为了寻求各向异性材料弹性力学偏微分方程一般解，需要扩展复变函数的概念和基本理论。现在引入一个泛复变量w与其共轭变量 $\bar{w}$，虚数单位i ( $i^2=-1$ )，用直角坐标表示如下：

$w=x+qy=x+gy+ihy,\bar{w}=x+\bar{q}y=x+gy-ihy$ (7)

复常数取为： $q=g+ih$， $\bar{q}=g-ih$，即 $g,h$ 为实数(且规定 $h>0$ )。容易得到以下关系式：

$q+\bar{q}=2g,q-\bar{q}=2hi,q\bar{q}=g^2+h^2$

泛复变量具有以下性质：

$w\bar{w}=\left(x+qy\right)\left(x+\bar{q}y\right)=x^2+2gxy+\left(g^2+h^2\right)y^2={\left(x+gy\right)}^2+h^2{y}^2$

采用变量代换： $X=x+gy$， $Y=hy$，则有：

$w=X+iY,\bar{w}=X-iY,w\bar{w}=X^2+Y^2$

因此可定义泛复变量的广义长度(模)为：

$L=\left|w\right|=\left|\bar{w}\right|=\sqrt{w\bar{w}}=\sqrt{{\left(x+gy\right)}^2+h^2{y}^2}=\sqrt{X^2+Y^2}$ (8)

引入复变函数 $\Psi \left(w\right)$，且为w的全纯函数。设实变函数 $F\left(x,y\right)$ 可用复变量的全纯函数表达，其偏导数就可转化为复变函数的导数形式，有如下关系式：

$\begin{array}{l}{F}_x=\frac{\partial F}{\partial x}=\frac{\partial F}{\partial w}\frac{\partial w}{\partial x}+\frac{\partial F}{\partial \bar{w}}\frac{\partial \bar{w}}{\partial x}=\frac{\partial F}{\partial w}+\frac{\partial F}{\partial \bar{w}}\\ F_y=\frac{\partial F}{\partial y}=\frac{\partial F}{\partial w}\frac{\partial w}{\partial y}+\frac{\partial F}{\partial \bar{w}}\frac{\partial \bar{w}}{\partial y}=q\frac{\partial F}{\partial w}+\bar{q}\frac{\partial F}{\partial \bar{w}}\end{array}\}$ (9)

因此可求得二阶偏导数为：

$\begin{array}{l}{F}_{xx}=\frac{{\partial }^{2}F}{\partial x^2}=\frac{{\partial }^{2}F}{\partial w^2}+2\frac{{\partial }^{2}F}{\partial w\partial \bar{w}}+\frac{{\partial }^{2}F}{\partial {\bar{w}}^2}\\ F_{yy}=\frac{{\partial }^{2}F}{\partial y^2}=q^2\frac{{\partial }^{2}F}{\partial w^2}+2q\bar{q}\frac{{\partial }^{2}F}{\partial w\partial \bar{w}}+{\bar{q}}^2\frac{{\partial }^{2}F}{\partial {\bar{w}}^2}\\ F_{xy}=\frac{{\partial }^{2}F}{\partial x\partial y}=q\frac{{\partial }^{2}F}{\partial w^2}+2g\frac{{\partial }^{2}F}{\partial w\partial \bar{w}}+\bar{q}\frac{{\partial }^{2}F}{\partial {\bar{w}}^2}\end{array}\}$ (10)

为了便于求解图1所示的各向异性板应力边值问题，选取应力函数F为：

$F=C\Psi \left(w\right)+\bar{C}\bar{\Psi }\left(\bar{w}\right)$ (11)

再对应力函数 $F\left(x,y\right)$ 求偏导数可得：

$F_x=C{\Psi }^{\prime }+\bar{C}\overline{{\Psi }^{\prime }},F_y=qC{\Psi }^{\prime }+\bar{q}\bar{C}\overline{{\Psi }^{\prime }}$

$\begin{array}{l}{F}_{xx}=C{\Psi }^{″}+\bar{C}{\bar{\Psi }}^{″}=C\Phi +\bar{C}\bar{\Phi }\\ F_{yy}=q^{2}C{\Psi }^{″}+{\bar{q}}^2\bar{C}{\bar{\Psi }}^{″}=q^{2}C\Phi +{\bar{q}}^2\bar{C}\bar{\Phi }\\ F_{xy}=qC{\Psi }^{″}+\bar{q}\bar{C}{\bar{\Psi }}^{″}=qC\Phi +\bar{q}\bar{C}\bar{\Phi }\end{array}$

式中， ${\Psi }^{″}={\Psi }^{″}\left(w\right)=\Phi \left(w\right)=\Phi$，再根据式(2)可将应力分量表示如下：

$\begin{array}{l}{\sigma }_x=q^{2}C\Phi +{\bar{q}}^2\bar{C}\bar{\Phi }=2\mathrm{Re}\left(q^{2}C\Phi \right)\\ {\sigma }_y=C\Phi +\bar{C}\bar{\Phi }=2\mathrm{Re}\left(C\Phi \right)\\ {\tau }_{xy}=-qC\Phi -\bar{q}\bar{C}\bar{\Phi }=-2\mathrm{Re}\left(qC\Phi \right)\end{array}\}$ (12)

再对应力函数求高阶偏导数，代入四次偏微分方程(5)就可导得下式：

$\left(q^4+A_1{q}^3+A_2{q}^2+A_{3}q+A_4\right)C{\Phi }^{″}+\left({\bar{q}}^4+A_1{\bar{q}}^3+A_2{\bar{q}}^2+A_3\bar{q}+A_4\right)\bar{C}{\bar{\Phi }}^{″}=0$

由此将微分方程转化成求解复数 $\left(q,\bar{q}\right)$ 的特征方程：

$\begin{array}{l}{q}^4+A_1{q}^3+A_2{q}^2+A_{3}q+A_4=0\\ {\bar{q}}^4+A_1{\bar{q}}^3+A_2{\bar{q}}^2+A_3\bar{q}+A_4=0\end{array}\}$ (13)

根据四次方程的求解方法可确定出四个根( $q_1,q_2,q_3={\bar{q}}_1,q_4={\bar{q}}_2$ )。现在将 $q_1,q_2$ 记为： $q_1=g_1+i{h}_1,q_2=g_2+i{h}_2$，且选取 $h_1>h_2>0$，可根据方程(13)的四个根来确定出各个参数值。显然四个实数 $g_1,g_2,h_1,h_2$ 与各向异性材料有关。

根据图1中标注的坐标系，具有以下关系：

$x_1=x-a=r_1\cos {\theta }_1,x_2=x-a-b=r_2\cos {\theta }_2$

$y=y_1=y_2=r_{1}sin{\theta }_1=r_2\sin {\theta }_2$

再将复变量表示为：

$\begin{array}{l}{w}_1=x_1+q_1{y}_1=x_1+g_1{y}_1+i{h}_1{y}_1=r_1\left(\cos {\theta }_1+g_1\sin {\theta }_1+i{h}_1\sin {\theta }_1\right)\\ w_2=x_1+q_2{y}_1=x_1+g_2{y}_1+i{h}_2{y}_1=r_1\left(\cos {\theta }_1+g_2\sin {\theta }_1+i{h}_2\sin {\theta }_1\right)\\ w_3=x_2+q_1{y}_2=x_2+g_1{y}_2+i{h}_1{y}_2=r_2\left(\cos {\theta }_2+g_1\sin {\theta }_2+i{h}_1\sin {\theta }_2\right)\\ w_4=x_2+q_2{y}_2=x_2+g_2{y}_2+i{h}_2{y}_2=r_2\left(\cos {\theta }_2+g_2\sin {\theta }_2+i{h}_2\sin {\theta }_2\right)\end{array}\}$ (14)

对于图1所示的面力边界条件，并根据式(12)的应力表达式，可选用以下四个复变函数作为应力函数：

${\Phi }_1=\ln w_1,{\Phi }_2=\ln w_2,{\Phi }_3=\ln w_3,{\Phi }_4=\ln w_4$

由此可将应力分量表达式改变成下列多复变函数形式：

$\begin{array}{l}{\sigma }_x=2\mathrm{Re}\left(q_1^2{C}_1\ln w_1+q_2^2{C}_2\ln w_2+q_1^2{C}_3\ln w_3+q_2^2{C}_4\ln w_4\right)\\ {\sigma }_y=2\mathrm{Re}\left(C_1\ln w_1+C_2\ln w_2+C_3\ln w_3+C_4\ln w_4\right)\\ {\tau }_{xy}=-2\mathrm{Re}\left(q_1{C}_1\ln w_1+q_2{C}_2\ln w_2+q_1{C}_3\ln w_3+q_2{C}_4\ln w_4\right)\end{array}\}$ (15)

式中 $C_1,C_2,C_3,C_4$ 为待定复常数。

为了推导出应力分量的简明表达式，需要进行恰当的坐标转换。对于式(14)的复变量，采用以下代换：

$\begin{array}{l}\cos {\theta }_1+g_1\sin {\theta }_1=J_{1}cos{\beta }_1,h_1\sin {\theta }_1=J_{1}sin{\beta }_1\\ \cos {\theta }_1+g_2\sin {\theta }_1=J_{2}cos{\beta }_2,h_2\sin {\theta }_1=J_{2}sin{\beta }_2\\ \cos {\theta }_2+g_1\sin {\theta }_2=J_{3}cos{\beta }_3,h_1\sin {\theta }_2=J_{3}sin{\beta }_3\\ \cos {\theta }_2+g_2\sin {\theta }_2=J_{4}cos{\beta }_4,h_2\sin {\theta }_2=J_{4}sin{\beta }_4\end{array}\}$ (16)

由此容易确定出下列关系式：

$\begin{array}{l}\tan {\beta }_1=\frac{h_1\sin {\theta }_1}{\cos {\theta }_1+g_1\sin {\theta }_1},J_1=\sqrt{{\left(cos{\theta }_1+g_{1}sin{\theta }_1\right)}^2+{\left(h_1\sin {\theta }_1\right)}^2}\\ \tan {\beta }_2=\frac{h_2\sin {\theta }_1}{\cos {\theta }_1+g_2\sin {\theta }_1},J_2=\sqrt{{\left(cos{\theta }_1+g_{2}sin{\theta }_1\right)}^2+{\left(h_2\sin {\theta }_1\right)}^2}\\ \tan {\beta }_3=\frac{h_1\sin {\theta }_2}{\cos {\theta }_2+g_1\sin {\theta }_2},J_3=\sqrt{{\left(cos{\theta }_2+g_{1}sin{\theta }_2\right)}^2+{\left(h_1\sin {\theta }_2\right)}^2}\\ \tan {\beta }_4=\frac{h_2\sin {\theta }_2}{\cos {\theta }_2+g_2\sin {\theta }_2},J_4=\sqrt{{\left(cos{\theta }_2+g_{2}sin{\theta }_2\right)}^2+{\left(h_2\sin {\theta }_2\right)}^2}\end{array}\}$ (17)

则可将复变量表示为：

$w_1=r_1{J}_1{\text{e}}^{i{\beta }_1},w_2=r_1{J}_2{\text{e}}^{i{\beta }_2},w_3=r_2{J}_3{\text{e}}^{i{\beta }_3},w_4=r_2{J}_4{\text{e}}^{i{\beta }_4}$ (18)

通过以上变换关系，可使应力分量表达式转化为：

$\begin{array}{l}{\sigma }_x=2\mathrm{Re}\left[q_1^2{C}_1\ln \left(r_1{J}_1\right)+q_2^2{C}_2\ln \left(r_1{J}_2\right)+q_1^2{C}_3\ln \left(r_2{J}_3\right)+q_2^2{C}_4\ln \left(r_2{J}_4\right)\right]\\ \begin{array}{cc}& \end{array}-2\mathrm{Im}\left({\beta }_1{q}_1^2{C}_1+{\beta }_2{q}_2^2{C}_2+{\beta }_3{q}_1^2{C}_3+{\beta }_4{q}_2^2{C}_4\right)\\ {\sigma }_y=2\mathrm{Re}\left[C_1\ln \left(r_1{J}_1\right)+C_2\ln \left(r_1{J}_2\right)+C_3\ln \left(r_2{J}_3\right)+C_4\ln \left(r_2{J}_4\right)\right]\\ \begin{array}{cc}& \end{array}-2\mathrm{Im}\left({\beta }_1{C}_1+{\beta }_2{C}_2+{\beta }_3{C}_3+{\beta }_4{C}_4\right)\\ {\tau }_{xy}=-2\mathrm{Re}\left[q_1{C}_1\ln \left(r_1{J}_1\right)+q_2{C}_2\ln \left(r_1{J}_2\right)+q_1{C}_3\ln \left(r_2{J}_3\right)+q_2{C}_4\ln \left(r_2{J}_4\right)\right]\\ \begin{array}{cc}& \end{array}+2\mathrm{Im}\left({\beta }_1{q}_1{C}_1+{\beta }_2{q}_2{C}_2+{\beta }_3{q}_1{C}_3+{\beta }_4{q}_2{C}_4\right)\end{array}\}$ (19)

下面根据图1的应力边界条件确定出式中的几个常数。

① 对于图1右边自由边界 $\left(x>a+b,y=0\right)$， ${\theta }_1=0,{\theta }_2=0$，则有：

${\beta }_1={\beta }_2={\beta }_3={\beta }_4=0,J_1=J_2=J_3=J_4=1$

${\sigma }_y=2\mathrm{Re}\left[\left(C_1+C_2\right)\ln r_1+\left(C_3+C_4\right)\ln r_2\right]=0$

${\tau }_{xy}=-2\mathrm{Re}\left[\left(q_1{C}_1+q_2{C}_2\right)\ln r_1+\left(q_1{C}_3+q_2{C}_4\right)\ln r_2\right]=0$

可得：

$\begin{array}{l}\mathrm{Re}\left(C_1+C_2\right)=0,Re\left(C_3+C_4\right)=0\\ \mathrm{Re}\left(q_1{C}_1+q_2{C}_2\right)=0,Re\left(q_1{C}_3+q_2{C}_4\right)=0\end{array}\}$ (20)

② 对于图1左边自由边界 $\left(x<a,y=0\right)$， ${\theta }_1=\pi ,{\theta }_2=\pi$，则有：

${\beta }_1={\beta }_2={\beta }_3={\beta }_4=\pi ,J_1=J_2=J_3=J_4=1$

${\sigma }_y=2\mathrm{Re}\left[\left(C_1+C_2\right)\ln r_1+\left(C_3+C_4\right)\ln r_2\right]-2\pi \mathrm{Im}\left(C_1+C_2+C_3+C_4\right)=0$

$\begin{array}{l}{\tau }_{xy}=-2\mathrm{Re}\left[\left(q_1{C}_1+q_2{C}_2\right)\ln r_1+\left(q_1{C}_3+q_2{C}_4\right)\ln r_2\right]\\ +2\pi \mathrm{Im}\left(q_1{C}_1+q_2{C}_2+q_1{C}_3+q_2{C}_4\right)=0\end{array}$

再利用关系式(20)进行简化，可得以下结果：

$\begin{array}{l}\mathrm{Im}\left(C_1+C_2+C_3+C_4\right)=0\\ \mathrm{Im}\left(q_1{C}_1+q_2{C}_2+q_1{C}_3+q_2{C}_4\right)=0\end{array}\}$ (21)

③ 对于图1中间受压边界 $\left(a<x<a+b,y=0\right)$， ${\theta }_1=0,{\theta }_2=\pi$，则有：

${\beta }_1={\beta }_2=0,{\beta }_3={\beta }_4=\pi ,J_1=J_2=J_3=J_4=1$

${\sigma }_y=2\mathrm{Re}\left[\left(C_1+C_2\right)\ln r_1+\left(C_3+C_4\right)\ln r_2\right]-2\pi \mathrm{Im}\left(C_3+C_4\right)=-p$

${\tau }_{xy}=-2\mathrm{Re}\left[\left(q_1{C}_1+q_2{C}_2\right)\ln r_1+\left(q_1{C}_3+q_2{C}_4\right)\ln r_2\right]+2\pi \mathrm{Im}\left(q_1{C}_3+q_2{C}_4\right)=0$

再利用关系式(20)进行简化，可得以下结果：

$2\pi \mathrm{Im}\left(C_3+C_4\right)=p,\mathrm{Im}\left(q_1{C}_3+q_2{C}_4\right)=0$ (22)

通过对上列关系式(20) (21) (22)组合求解，可确定出常数 $C_1,C_2,C_3,C_4$，这些都是复数，推导的结果如下：

$\begin{array}{l}{C}_1=\frac{p}{2\pi }\frac{D_3-i{D}_2}{D_{12}},C_2=-\frac{p}{2\pi }\frac{D_3+i{D}_1}{D_1{}_2}\\ C_3=-\frac{p}{2\pi }\frac{D_3-i{D}_2}{D_{12}}=-C_1,C_4=\frac{p}{2\pi }\frac{D_3+i{D}_1}{D_1{}_2}=-C_2\end{array}\}$ (23)

式中的实常数 $D_1,D_2,D_{12},D_3$ 与材料参数 $g_1,g_2,h_1,h_2$ 相关，确定为：

$\begin{array}{l}{D}_1=g_1\left(g_1-g_2\right)+h_1\left(h_1-h_2\right),D_2=g_2\left(g_2-g_1\right)+h_2\left(h_2-h_1\right)\\ D_{12}=D_1+D_2={\left(g_1-g_2\right)}^2+{\left(h_1-h_2\right)}^2,D_3=g_2{h}_1-g_1{h}_2\end{array}\}$ (24)

将确定的四个复数代入式(19)后，应力表达式就转化为：

$\begin{array}{l}{\sigma }_x=\frac{p}{\pi }\mathrm{Re}\left[\frac{D_3-i{D}_2}{D_{12}}{q}_1^2\ln \frac{r_1{J}_1}{r_2{J}_3}-\frac{D_3+i{D}_1}{D_1{}_2}{q}_2^2\ln \frac{r_1{J}_2}{r_2{J}_4}\right]\\ -\frac{p}{\pi }\mathrm{Im}\left[\frac{D_3-i{D}_2}{D_{12}}{q}_1^2\left({\beta }_1-{\beta }_3\right)-\frac{D_3+i{D}_1}{D_1{}_2}{q}_2^2\left({\beta }_2-{\beta }_4\right)\right]\end{array}$

$\begin{array}{l}{\sigma }_y=\frac{p}{\pi }\mathrm{Re}\left[\frac{D_3-i{D}_2}{D_{12}}\ln \frac{r_1{J}_1}{r_2{J}_3}-\frac{D_3+i{D}_1}{D_1{}_2}\ln \frac{r_1{J}_2}{r_2{J}_4}\right]\\ -\frac{p}{\pi }\mathrm{Im}\left[\left({\beta }_1-{\beta }_3\right)\frac{D_3-i{D}_2}{D_{12}}-\left({\beta }_2-{\beta }_4\right)\frac{D_3+i{D}_1}{D_1{}_2}\right]\end{array}$

$\begin{array}{l}{\tau }_{xy}=-\frac{p}{\pi }\mathrm{Re}\left[\frac{D_3-i{D}_2}{D_{12}}{q}_1\ln \frac{r_1{J}_1}{r_2{J}_3}-\frac{D_3+i{D}_1}{D_1{}_2}{q}_2\ln \frac{r_1{J}_2}{r_2{J}_4}\right]\\ +\frac{p}{\pi }\mathrm{Im}\left[\frac{D_3-i{D}_2}{D_{12}}{q}_1\left({\beta }_1-{\beta }_3\right)-\frac{D_3+i{D}_1}{D_1{}_2}{q}_2\left({\beta }_2-{\beta }_4\right)\right]\end{array}$

再对上列表达式中的各个复数分解，经推导可得以下结果：

$\begin{array}{l}{h}_1{D}_3-g_1{D}_2=h_2{D}_3+g_2{D}_1=g_2\left(g_1^2+h_1^2\right)-g_1\left(g_2^2+h_2^2\right)=D_4\\ g_1{D}_3+h_1{D}_2=g_2{D}_3-h_2{D}_1=h_1\left(g_2^2+h_2^2\right)-h_2\left(g_1^2+h_1^2\right)=D_5\\ \left(D_3-i{D}_2\right)q_1=\left(D_3+i{D}_1\right)q_2=D_5+i{D}_4\\ D_6=g_2{D}_4+h_2{D}_5,D_7=g_1{D}_4+h_1{D}_5\\ D_8=g_1{D}_5-h_1{D}_4,D_9=g_2{D}_5-h_2{D}_4\end{array}\}$ (25)

由此可见，应力分量就容易简化成下列表达式：

$\begin{array}{l}{\sigma }_x=-\frac{p}{\pi }\left[\frac{D_6}{D_1{}_2}\left({\beta }_4-{\beta }_2\right)-\frac{D_7}{D_{12}}\left({\beta }_3-{\beta }_1\right)-\frac{D_8}{D_{12}}\ln \frac{r_1{J}_1}{r_2{J}_3}+\frac{D_9}{D_1{}_2}\ln \frac{r_1{J}_2}{r_2{J}_4}\right]\\ {\sigma }_y=-\frac{p}{\pi }\left[\frac{D_1}{D_{12}}\left({\beta }_4-{\beta }_2\right)+\frac{D_2}{D_{12}}\left({\beta }_3-{\beta }_1\right)-\frac{D_3}{D_{12}}\ln \frac{J_1{J}_4}{J_2{J}_3}\right]\\ {\tau }_{xy}=\frac{p}{\pi }\left[\frac{D_4}{D_1{}_2}\left({\beta }_1-{\beta }_2-{\beta }_3+{\beta }_4\right)-\frac{D_5}{D_{12}}\ln \frac{J_1{J}_4}{J_2{J}_3}\right]\end{array}\}$ (26)

该表达式就是各向异性板局部边界加载的应力场解答，完全由实函数组成。

4. 计算举例

为了更好理解以上公式中各个参数的特点及应力场分布情况，现在举例说明计算方法。选取各向异性板的柔度系数为：

$\begin{array}{l}{a}_{11}=60{\left(TPa\right)}^{-1},a_{22}=120{\left(TPa\right)}^{-1},a_{66}=160{\left(TPa\right)}^{-1}\\ a_{12}=-20{\left(TPa\right)}^{-1},a_{16}=a_{26}=-30{\left(TPa\right)}^{-1}\end{array}$

则可求得：

$A_1=-\frac{2a_{16}}{a_{11}}=1,A_2=\frac{a_{66}+2a_{12}}{a_{11}}=2,A_3=-\frac{2a_{26}}{a_{11}}=1,A_4=\frac{a_{22}}{a_{11}}=2$

将以上数据代入式(13)可得：

$q^4+A_1{q}^3+A_2{q}^2+A_{3}q+A_4=q^4+q^3+2q^2+q+2=0$

对四次方程求解，可得四个根为：

$q_1=0.2762+1.07223i,q_2=-0.7762+1.01447i$

$q_3=0.2762-1.07223i,q_4=-0.7762-1.01447i$

由此可得： $g_1=0.2762,h_1=1.07223,g_2=-0.7762,h_2=1.01447$

将四个数据代入式(17)可确定出：

$\tan {\beta }_1=\frac{1.07223\sin {\theta }_1}{\cos {\theta }_1+0.2762\sin {\theta }_1},J_1=\sqrt{{\left(cos{\theta }_1+0.2762sin{\theta }_1\right)}^2+{\left(1.07223\sin {\theta }_1\right)}^2}$

$\tan {\beta }_2=\frac{1.01447\sin {\theta }_1}{\cos {\theta }_1-0.7762\sin {\theta }_1},J_2=\sqrt{{\left(cos{\theta }_1-0.7762sin{\theta }_1\right)}^2+{\left(1.01447\sin {\theta }_1\right)}^2}$

代换参数 ${\beta }_1,{\beta }_2,J_1,J_2$ 与角度 ${\theta }_1$ 的变化关系如图2所示。而参数 ${\beta }_3,{\beta }_4,J_3,J_4$ 与角度 ${\theta }_2$ 的变化关系曲线与图2相似。

再利用数据 $g_1=0.2762,h_1=1.07223,g_2=-0.7762,h_2=1.01447$ 按式(24)和式(25)计算其它实常数，其结果如下：

$\begin{array}{l}{D}_1=0.3526,D_2=0.7584,D_{12}=1.111\\ D_3=-1.1125,D_4=-1.4023,D_5=0.5058\\ D_6=1.602,D_7=0.155,D_8=1.643,D_9=1.03\end{array}$

并将这些数据代入式(26)，确定出应力分量表达式如下：

$\begin{array}{l}{\sigma }_x=-p\left[1.442\frac{{\beta }_4-{\beta }_2}{\pi }-0.14\frac{{\beta }_3-{\beta }_1}{\pi }-0.471\ln \frac{r_1{J}_1}{r_2{J}_3}+0.295\ln \frac{r_1{J}_2}{r_2{J}_4}\right]\\ {\sigma }_y=-p\left[0.3174\frac{{\beta }_4-{\beta }_2}{\pi }+0.6826\frac{{\beta }_3-{\beta }_1}{\pi }+0.319\ln \frac{J_1{J}_4}{J_2{J}_3}\right]\\ {\tau }_{xy}=-p\left[1.2622\frac{{\beta }_1-{\beta }_2-{\beta }_3+{\beta }_4}{\pi }+0.145\ln \frac{J_1{J}_4}{J_2{J}_3}\right]\end{array}\}$ (27)

以上说明了应力分量中的各个参数计算方法。

Figure 2. Relationship curves of parameter variations in coordinate replace

图2. 坐标代换参数变化关系曲线

5. 结论

先进复合材料广泛应用于工程承载结构中，并以板壳形式为主，因此对于各向异性板的弹性力学分析显得更加重要。利用多复变函数论求解各向异性材料弹性力学应力边值问题基本方程已成为一种有效途径。本文根据各向异性材料力学性能确定平面应力弹性力学的基本方程，叙述了求解偏微分方程的多复函理论。选择典型的平板边界局部受力实例，按各向异性板应力边值构建求解思路，通过多复变函数方法确定出应力场的实函数通解，并举例说明表达式中各个参数的计算方法。本文的关键步骤是对多复变量进行坐标变换，即采用变量代换关系式(16)，将多复变量转化为指数形式，使得复变函数的实部和虚部就容易分开，这一步对推导应力表达式(26)至关重要，这也是本文主要创新点。本文解析方法简明，所得结果比较完善，可推广用于一般各向异性体力学基础理论研究。