1. 主成分分析的主要步骤和相关概念
主成分分析,从一个原始数据矩阵
出发,
是m行n列的。其中,每一行是一个样本,每一列是一个变量,即共有m个样本、n个变量。
主要步骤如下 [1]:
1) 将原始数据做标准化处理,即令:
,得到X;
2) 建立变量的相关系数阵R,即X的协方差矩阵;
3) 求R的特征根为
,相应的特征向量为
;
4) 得到n个主成分为
,
。
上面步骤涉及到的主要概念如下:
1) 载荷矩阵:就是上面的特征向量矩阵
,是n行n列的;
2) 主成分得分:
,即样本在第i个主成分上的得分,也是数据X经过第i个特征向量变换后的数据;
3) 因子载荷量:
,即为主成分
与原始变量
的相关系数;
4) 累计贡献率:
,
且
,就是前p个特征值的和在所有特征值和里的占比。
2. 基于主成分分析的数据降维
本节从主成分的数据降维理论过程、其应用场景和最后的R语言实践三个方面进行阐述。
1) 用主成分进行数据降维的步骤如下:
根据已知
的数据
,每一行是一个样本,每一列是一个变量。根据
进行以下步骤的操作,进行对
的降维。
上接主成分分析的主要步骤的第(4)步,n个主成分不一定全部选用,而是根据特征值的累计贡献率来决定选取主成分的个数。后续实施过程见如下两步:
a) 计算特征值的累计贡献率:
当累计到某个i,使得累计贡献率 ≥ 0.85时,就把这个i取出来,为后续降维步骤做准备;
b) 取部分特征值并进行数据变换:
让特征向量T里只取前i个出来得到
,用
对数据X做变换,得到
,因为
是
的,X是
的,所以彼此转置再乘。这里得到的Y是
的,再转置一下Y,得到
的,就是变换完的数据、降维后的数据,用于代替原来的X去做其他数据分析的用途。
2) 基于主成分降维的应用场景
在主成分分析适用的场合,可以用较少的、互不相关的主成分来代替较多的、有相关性的原始变量。既降低了数据维数,又能保留原数据的大部分信息,从而降低了选取指标的难度,减少了计算的工作量。目前,运用主成分分析对数据进行降维广泛应用于图像压缩、模式识别、食品和医学等各个领域。
在文献 [2] 中,作者介绍了一种基于PCA-SVM的手写数字识别系统模型。运用PCA将784维的数据降至25维,大大减少了冗杂数据对特征提取的影响,并明显的改善了实验时效和设备的运行损耗。
在文献 [3] 中,作者设计了数据流降维算法PSPCA。使用滑动窗口机制确定处理数据的范围,合并了标准化和相关系数矩阵的计算步骤。实验结果表明,PSPCA适用于数据流降维,并能保留合理范围内的原数据信息量,同时保证后续数据挖掘的准确性。
但传统的主成分分析算法存在一定的局限性。比如处理超高维稀疏数据时耗时过长、特征子集的有效性不强等,不少学者提出了相应的改进措施。
在文献 [4] 中,对于降维前用信息熵做特征筛选的PCA改进算法,作者认为其没有考虑特征与类间的关系,导致分类准确率不高。对于用互信息矩阵代替协方差矩阵的PCA改进方法,认为其虽然有效提高了降维结果和分类准确率,但特征子集的有效性不好。因此,在引入绝对互信息可信度和相对互信息可信度的基础上,该文给出互信息综合可信度,用其对数据特征进行筛选,最后对筛选出的特征进行PCA降维。
在文献 [5] 中,作者提出一种基于最优RBF核主成分的非线性降维重构方法,解决了传统核主成分的核参数选择困难问题,实验结果证明降维结果的准确性优于线性降维方法。
3) 基于主成分降维后预测的应用场景
维度低的数据,在采集时就可以有意选择相关性低的指标。数据维度较高时,想要控制指标间完全不相关或相关性低就较为困难。所以,如果原始数据各个指标不相关,或者相关性很低,利用主成分降维后,会损失较多信息,造成预测精度降低;如果原始数据维度高且指标间有较大相关性,主成分分析可以减少冗杂信息,消除指标间的相关性,提高预测准确度的效果就较好。近年有学者将PCA与逐步回归法、BP神经网络、机器学习等方法结合进行相关预测。
文献 [6] 中,作者提出了基于主成分分析的组合预测方法。首先对单项模型的预测结果进行PCA求出主成分,然后用AIC准则确定建模的主成分数量,最后建立沉降实测值与主成分之间的多元回归预测模型,实验结果表明,组合模型预测精度明显优于各单项模型。
文献 [7] 中,作者利用PCA对原始数据进行预处理,建立了基于主成分分析和粒子群支向量机的岩爆预测模型。实验结果表明,此模型的预测准确率高于SVM模型和ANN模型。
4) 基于主成分降维后的数据进行预测的R语言实践
下面根据UCI上的一个数据Waveform,见图1,进行主成分分析的降维,并在降维前后结合BP网络对数据样本进行分类,考察分类的预测效果。
原始数据(波形数据库发生器数据集)一共有5000个样本,每个样本有41个属性,最后一个属性为样本类别。一共有3个类别(0,1,2)。

Figure 1. Part screenshot of UCI dataset Waveform
图1. UCI数据集Waveform部分截图
1) 将原始数据代入神经网络进行训练,代码如下:
wave <- read.csv(file = 'waveform.csv')
normalize <- function(x) {
return ((x - min(x)) / (max(x) - min(x)))
}
wave_n <- as.data.frame(lapply(wave[,1:40], normalize))
table(wave$class)#统计各类别样本量
library(nnet);
n=length(wave[,1]); #样本量
set.seed(1);#设随机数种子
samp=sample(1:n,n/2);#随机选择半数观测作为训练集
b=class.ind(wave[,41]);#生成类别的示性函数
a=nnet(wave_n[samp,],b[samp,],size=8,rang=0.1,decay=5e-4,maxit=200);#利用训练集中前18个变量作为输入变量,隐藏层有3个节点,初始随机权值在[-0.1,0.1],权值是逐渐衰减的。
table(max.col(b[samp,]),max.col(predict(a,wave_n[samp,])))
table(max.col(b[-samp,]),max.col(predict(a,wave_n[-samp,])))
pred<-predict(a,wave_n[samp,])
test1<-table(max.col(b[samp,]),max.col(predict(a,wave_n[samp,])))
test2<-table(max.col(b[-samp,]),max.col(predict(a,wave_n[-samp,])))
cat(训练样本正确率,sum(diag(test1))/sum(test1))
cat(测试样本正确率,sum(diag(test2))/sum(test2))
得到测试样本正确率为:0.8244。
2) 对原始数据进行PCA降维处理
根据累计方差贡献率 ≥ 0.85,选择主成分个数为25个。代码如下:
#然后对wave_n做pca,再然后神经网络训练和测试
library(psych)
library(tidyverse)
d<-wave_n
d.pr=princomp(d,cor=TRUE)#主成分分析
#screeplot(d.pr,type='lines')#碎石图
#summary(d.pr,loadings=TRUE) 结果
y=eigen(cor(d))#特征值和特征向量
y$values
#y$vectors
sum(y$values[1:25])/sum(y$values)#累计方差贡献率
s=d.pr$scores#主成分得分
s=s[,1:25]
wave_pca=data.frame(s)
wave_pca$Class <- wave$class
3) 将PCA降维后的数据代入神经网络进行训练
normalize <- function(x) {
return ((x - min(x)) / (max(x) - min(x)))
}
wave_pca_n <- as.data.frame(lapply(wave_pca[,1:25], normalize))
table(wave$class)
library(nnet);
n=length(wave[,1]); #样本量
set.seed(1);#设随机数种子
samp=sample(1:n,n/2);#随机选择半数观测作为训练集
b=class.ind(wave_pca[,26]);#生成类别的示性函数 #Find the maximum position for each row of a matrix, breaking ties at random.喂进去的数据必须是个矩阵
a=nnet(wave_pca_n[samp,],b[samp,],size=8,rang=0.1,decay=5e-4,maxit=200);#利用训练集中前18个变量作为输入变量,隐藏层有3个节点,初始随机权值在[-0.1,0.1],权值是逐渐衰减的。
table(max.col(b[samp,]),max.col(predict(a,wave_pca_n[samp,])))
table(max.col(b[-samp,]),max.col(predict(a,wave_pca_n[-samp,])))
pred<-predict(a,wave_pca_n[samp,])
test1<-table(max.col(b[samp,]),max.col(predict(a,wave_pca_n[samp,])))
test2<-table(max.col(b[-samp,]),max.col(predict(a,wave_pca_n[-samp,])))
cat(训练样本正确率,sum(diag(test1))/sum(test1))
cat(测试样本正确率,sum(diag(test2))/sum(test2))
得到测试样本的正确率为:0.8296。
由0.8296 > 0.8244可知,利用主成分分析对数据进行降维并消除相关性的处理后,预测正确率会得到一定的提升,但提升幅度不大。原始数据变量各个之间相关性较强时,利用主成分降维后,正确率会有明显提升。
3. 基于主成分分析的综合评价
本节从主成分分析综合评价的理论过程,其使用情况和最后的R语言实践三个方面进行阐述。
1) 综合评价的理论过程 [1]
在得到主成分分析过程的变换后的数据Y (各个主成分)和特征值后
以后,根据如下方法得到评价函数Z,原来的数据样本X,每一个观测都会得到一个Z值,作为对每个样本的评价得分,根据这个得分看出原来X里每个样本的重要性。
设
是所求出的n个主成分,它们的特征根分别是
。将特征根“归一化”即有
记为
,由
,构造综合评价函数为
令
,并代入综合评价函数,有:
这里我们应该注意,从本质上来说,综合评价函数是对原始指标的线性综合,从计算主成分到对之加权,经过两次线性运算后得到综合评价函数。然后,每个样本经过这个计算得到一个相应的Z值,根据Z值的大小,可以对样本进行排序和比较,从而实现对样本的优先顺序评价。
2) 基于主成分分析的综合评价使用情况
一般情况下,选择评价指标体系后要对各指标加权来进行综合。指标加权要依据指标的重要性,而对重要性的判断往往带有一定的主观性。而主成分分析能从选定的指标体系中归纳出大部分信息,根据指标间的相对重要性进行客观加权。各主成分的权数为其贡献率,它反映了该主成分包含原始数据的信息量占全部信息量的比重,这样确定权数是客观的、合理的。另外,还有些文献在主成分分析中的综合评价得分基础上,又进行了其他改进,以便更好地评价自己的数据样本。这些文献的使用场景如下:
文献 [8] 中,通过主成分分析将牡丹的10个主要性状降维为4个主成分,并以主成分贡献率为权重,建立了高产评价模型,然后依据综合评价得分来划分牡丹等级。
也有许多学者将主成分分析与其他方法结合起来,确定更加合理的评价指标权重。
文献 [9] 中,作者运用主成分分析对原始指标进行降维,简化了信用评价体系,在确定权重时借助熵权法对评价指标进行客观赋权,求得综合评价函数。
文献 [10] 中,作者采用层次分析法和熵权法对指标变量进行分层赋权,合理地考虑了指标的重要性差异。
3) 基于主成分分析的综合评价的R语言实践
下面这个例子来自文献 [1],不同于原文献的是,我们用R语言实现一遍其综合评价过程,代码以供其他研究者们参考和使用。
采用某市工业部门13个行业的8项重要经济指标的数据,见表1。8项经济指标为:
X1:年末固定资产净值,单位:万元;
X2:职工人数据,单位:人;
X3:工业总产值,单位:万元;
X4:全员劳动生产率,单位:元/人年;
X5:百元固定资产原值实现产值,单位:元;
X6:资金利税率,单位:%;
X7:标准燃料消费量,单位:吨;
X8:能源利用效果,单位:万元/吨。

Table 1. The original data for comprehensive evaluation based on PCA
表1. 主成分综合评价原始数据
把数据读入R里,记为d。对d作主成分分析,求出特征值和主成分得分。再用特征值求得综合评价指标即主成分的权重,乘以相应的主成分得分,加和得到综合评价得分。代码如下:
d<-read.csv('工业指标.csv',sep=',',row.names = 1)
d<-data.frame(d)
d<-scale(x=d)
d.pr=princomp(d,cor=TRUE)#主成分分析
#summary(d.pr,loadings=TRUE) 结果
y=eigen(cor(d))#特征值和特征向量
y$values
y$vectors
sum(y$values[1:3])/sum(y$values)#累计方差贡献率
s=d.pr$scores#主成分得分
options(digits = 4)
scores=0.0
for(i in 1:8)
scores = (y$values[i]*s[,i])/(sum(y$values[1:8]))+scores#计算综合得分
score=cbind(s,scores)#综合得分信息
score
rank(-score[,9])
得到主成分得分和综合评价得分,见表2:

Table 2. Principal component scores and comprehensive evaluation scores
表2. 主成分得分和综合评价得分
对上面的综合评价得分进行排序:

从综合评价得分可知,机器行业在该地区的综合评价排在第一。另外,从原始数据和前两个主成分得分上也能看出,该行业存在明显的优势。而该地区综合评价排在最后一位的则是煤炭行业,其第二主成分的得分为负数,说明低于平均水平。
4. 基于主成分分析的关键特征确定
本节从利用主成分分析确定关键特征的理论依据,其应用场景和相应的R语言实践三个方面进行阐述。
1) 关键特征确定的理论依据
关键特征的确定,主要和主成分得分和因子载荷有关。
原始数据矩阵X是
的,载荷矩阵T是
的。X的转置就是
的。
,
的每一列是一个样本,每一行是一个变量。
的每一行是一个特征向量的转置。作主成分变换
可得:
先看主成分得分:
上式右边的矩阵中,第i行、第j列代表样本j在第i个主成分上的得分。比如第2行第1列中的
的值比较大,代表的就是样本1在PC2上的得分较高。
再看因子载荷量:
由因子载荷量公式:
可推出:
。所以:
因为主成分分析前所做的数据标准化,会使数据的每一个变量均值变为0,方差即
变为1,所以有:
其中,
是原始变量
的分量,
,
是原始变量
的分量。
那么,
即第二主成分和第一原始变量的因子载荷大,就代表原始变量
为样本1的关键特征。
总的来说,做完主成分变换后,就可以用主成分来解释样品差异。所以可以观察不同样本在第几主成分上的得分高。然后去看这个主成分上因子载荷量大的原始变量有哪些。这些原始变量,就对应样本的关键特征。找到关键特征后,可以根据关键特征对事物进行进一步的研究和改变。
从载荷和得分双重图上,也能直观地看出不同类别的关键特征。
2) 基于主成分分析关键特征确定的应用场景
利用主成分分析对数据进行降维并保留大部分原始信息,易于突出主要特征。因子载荷量(主成分与原始变量的相关系数)较大值对应的原始变量,可以认为是关键特征。下面是一些文献中的应用场景:
文献 [11] 中,作者对不同香型白酒的29种主要风味物质进行主成分分析,提取出2个主成分,并画出了主成分载荷和白酒酒样得分双重图,得到了乙酸乙酯、乙酸是清香型白酒的主体风味物质,苯乙醇是芝麻香型白酒的关键风味物质等结论。
文献 [12] 中,采用KMO和Bartlett球形度对茎瘤芥的12中营养元素间的相关性进行检验,结果表明适合对原始变量进行主成分分析。然后采用PCA提取出2个主成分,用最大方差法对因子载荷矩阵旋转,构建出主成分得分模型。模型显示出的具有较大载荷值的变量为茎瘤芥的特征元素。
3) 基于主成分分析确定关键特征的R语言实践
下面使用文献 [11] 的数据,见图2,进行R语言实践,从主成分得分及因子载荷量数据、得分和载荷双重图两方面进行实验,并给出一个样本的关键特征结果,以展现本节对于关键特征确定的R语言实验代码效果。
采用16种不同种类白酒的29种风味物质质量浓度(mg/L)数据。
16种不同种类白酒为:
浓香型白酒:
;清香型白酒:
;酱香型白酒:
;
芝麻香型白酒:Z1;特香型白酒:T1
29种风味物质为:
酯类物质9种:己酸乙酯(F1)、甲酸异戊酯(F2)、乳酸乙酯(F3)、丁酸乙酯(F4)、乙酸乙酯(F5)、戊酸乙酯(F6)、庚酸乙酯(F9)、辛酸乙酯(F11)、棕榈酸乙酯(F14);
醇类物质9种:正丙醇(F18)、活性戊醇(F19)、异丁醇(F21)、 2,3-丁二醇(F22)、甲醇(F23)、正己醇(F24)、苯乙醇(F27)、(2R,3R)-(-)-2,3-丁二醇(F29)、3-呋喃甲醇(F31);
酸类物质6种:己酸(F33)、丁酸(F34)、乙酸(F35)、正戊酸(F37)、3-甲基戊酸(F38)、辛酸(F39);
酮类物质1种:3-羟基-2-丁酮(F41);
醛类物质2种:乙醛(F43)、3-糠醛(F45);
其它类物质2种:1 ,1-二乙氧基乙烷(F50)、1 ,1-二乙氧基-3-甲基丁烷(F51)。

Figure 2. Screenshot of the flavour substance sample data section
图2. 风味物质样本数据部分截图
1) 从主成分得分和因子载荷数据可以进行分析:
library(psych)
library(tidyverse)
library(factoextra)
data<-read.csv('白酒.csv',sep=',',row.names=1)
data<-data.frame(data)
data<-scale(x=data)
fa.parallel(data,fa='pc')
p<-principal(data,nfactors=2,rotate=none)
p$values
sum(p$values[1:2])/sum(p$values)
p$loadings#p$weights
p$scores
例如,想要找浓香型白酒N1的关键特征。先看实验得到的主成分得分,见表3。
可以看出,浓香型白酒N1的PC2得分较高,所以去看PC2上的因子载荷量,见表4。
由数据可知,
等物质在PC2上的因子载荷量较大,是浓香型白酒N1的关键特征。
2) 对原始数据作主成分分析,从因子载荷量和主成分得分图可以直观看出关键特征。
data<-read.csv('白酒.csv',sep=',',row.names=1)
res.pca=prcomp(data,scale=TRUE)
fviz_pca_var(res.pca, col.var = black)#因子载荷图
fviz_pca_biplot(res.pca,
palette=joo,
mean.point=F,
gradient.cols = RdYlBu,
ggtheme = theme_minimal())#双重图
得到因子载荷图及因子载荷和酒样得分双重图,见图3、图4。
从图3中可以看到各原始变量对PC1和PC2的影响是正还是负。例如,处在第四象限,表明它对PC1有很大的正向影响,对PC2有较大的负向影响。
图4表明:己酸乙酯和己酸等物质对PC2有较大的正向影响。这类物质与的距离较近,是浓香型白酒的主体风味物质。这与主成分得分和因子载荷数据分析出的结果相同。

Figure 4. The overlay graph of factor loadings and principal component scores
图4. 因子载荷和主成分得分双重图
5. 基于主成分分析的样本聚类
本节从主成分分析的样本聚类原理,其使用场景和利用主成分分析对酒样进行聚类的R语言实践三个方面进行阐述。
1) 基于主成分分析对样本进行聚类的原理
由于主成分包含原始数据的大部分信息,所以可以用主成分来解释样本之间的差异。样本在主成分得分图上的坐标就是它的主成分得分,同类样本的各主成分得分相似,在图上的距离就会相近,同类样本自然可以聚在一起。
2) 利用主成分分析进行样本聚类的使用场景
对多变量数据,可以选取前两个主成分,根据主成分得分画出样品在二维平面上的分布情况,从而直观地看出样品的分类情况。也可以根据关键特征有效地区分不同类别。但其分类效果不如聚类分析等方法,所以一般情况下会结合其他方法进行类别区分。
文献 [11] 中,作者结合聚类分析和主成分分析对白酒的风味物质进行研究。实验结果表明,主成分分析对白酒样品香型的分类效果不如聚类分析,但可以反映白酒香型与风味物质之间的关系。
文献 [12] 中,由PCA构建的主成分得分模型,可以有效区分3个产地的茎瘤芥。由聚类分析可根据茎瘤芥中营养元素的含量差异进行产地溯源。
文献 [13] 中,作者对主成分分析中的正交旋转和斜交旋转做了对照,结果证明,斜交旋转比正交旋转划分的天气形势更具代表性。
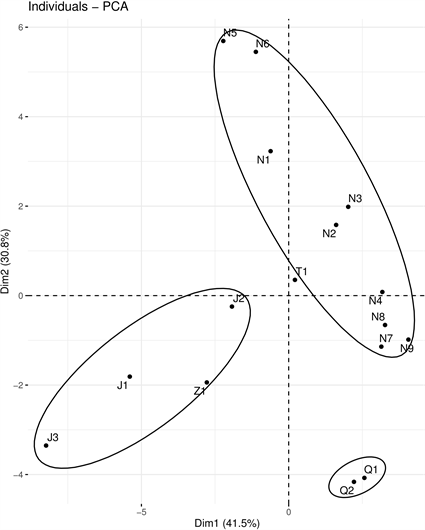
Figure 5. The diagram of the principal component scores of liquor samples
图5. 各白酒样本的主成分得分图
3) 基于主成分得分对样本进行聚类的R语言实验
与“基于主成分分析确定关键特征的R语言实验”数据相同,对其作主成分分析,可以画出主成分得分图。
data<-read.csv('白酒.csv',sep=',',row.names=1)
res.pca=prcomp(data,scale=TRUE)
#res.pca$x[,1:2] 看各样本在第一、第二主成分上的得分
fviz_pca_ind(res.pca, repel=T) #个体图
主成分得分图上,各样本的坐标就是其在第一、第二主成分上的得分。
得到主成分得分图,见图5。
从图中可以看出,清香型白酒
分布集中;特香型白酒T1靠近浓香型白酒
;酱香型白酒
分布较为分散,但都分布在第4象限;芝麻香型白酒Z1与酱香型白酒距离较近且位于第4象限,说明它们的风味组分构成相似。
6. 总结
本文对主成分分析的主要过程和相关概念进行了概述,对主成分分析在降维、综合评价、关键特征确定和样本聚类方面的应用进行了理论推导,还给出了在R语言上实现这些应用的实例。这些工作把主成分分析的理论和实际应用联系起来,展示了主成分分析的优点:可以减少指标选择的工作量、简化计算、消除数据的相关性和冗杂信息、突出关键特征等。我们对这些过程进行详细论述并给出相关的R语言实践代码及相应分析等,有助于主成分分析的广大学习者和使用者更好地理解和应用这些方法。