基于QPSO-BP的云平台信息系统安全风险分析

Security Risk Analysis of Cloud Platform Information System Based on QPSO-BP

摘要: 云平台是云计算服务的重要载体，具有更开放、虚拟化、高度集成以及平台架构复杂等特性，更易受到各种威胁。论文在分析云平台架构及其服务模式的基础上，提出基于云平台信息系统的风险分析模型，引入量子粒子群优化BP神经网络(QPSO-BP)模型对信息系统安全风险进行分析，通过分析各风险因素对系统风险的影响，获得云平台风险因素敏感度评价，实现对风险的预测和管理。仿真表明，该方法能有效预测云平台信息系统风险，与GA-BP和PSO-BP神经网络预测方法相比有较好的网络性能和预测精度，为云平台信息系统风险管理提供一种科学有效的理论方法。

Abstract: Cloud platform is an important carrier of cloud computing services, which is more open, virtualized, highly integrated and complex in platform architecture. It is more vulnerable to various threats. Based on the analysis of cloud platform architecture and its service mode, this paper puts forward a risk analysis model based on cloud platform information system and introduces QPSO-BP model to analyze information system security risk. By analyzing the influence of various risk factors on system risk, the sensitivity evaluation of cloud platform risk factors is obtained, the risk prediction and management are realized. Simulation results show that this method can effectively predict the risk of cloud platform information system. Compared with GA-BP and PSO-BP neural network prediction methods, it has better network performance and prediction accuracy, provides a scientific and effective theoretical method for risk management of cloud platform information system.

1. 引言

云平台是一种基于互联网的后信息技术，相较于其他传统计算模式，具有动态可扩展、资源高度集中以及提供外包服务等特性，通过云平台，云计算服务提供商可向用户提供所需的服务，实现按需分配资源 [1]。基于分布式服务器的云平台允许多用户从接入口获取数据资源并提供可视化窗口，同时云平台的用户群非常广泛，其中也掺杂着恶意的破坏者，并且服务器分布范围广等，导致云平台的监管力度不足，加剧云平台信息安全的管理难度 [2]。较高的集成度以及大量的底层支撑技术也使得云平台的基础架构组成相对复杂，在当前的网络环境中更容易受到各类安全威胁，其安全性问题已然成为制约云计算发展的瓶颈。

信息系统日益更新以及网络环境的愈发复杂，导致网络安全威胁所带来的损失不断增加，信息系统的风险分析理论与方法倍受关注。刘国城 [3] 等人将层次分析法进行信息系统层级分类，并邀请专家为各层级因素打分赋权值，再计算其熵权值和风险向量，对风险向量进行排序比较得到其风险等级。尽管该方法实用性强可用性高，但该信息系统的层次系统结构设计科学性无法保证且熵权理论不能对每层中各指标进行横向比较，降低了风险评估的客观性。伍浏阳 [4] 采用因子分析法消除了风险因素间的相关性，再使用支持向量机方法进行网络训练，建立信息系统风险评价模型；该方法在一定程度上提高了信息系统风险评估的效率，但将众多风险因素提炼为几个指标会忽略小概率风险的影响因子，不利于风险评估与管理。令狐金花 [5] 等人用矩阵范式求解系统资产的证据距离并使用D-S证据理论计算威胁系统的证据距离，再将两种距离进行融合后计算出系统的风险值；该方法解决风险评估中专家评价意见主观性问题，但在其风险分析过程中没有考虑系统资产价值的损失对风险值的影响。王鑫 [6] 等人将模糊理论和贝叶斯正则化BP神经网络相结合进行风险评估，减少主观因素对评估结果的影响，增加指标量化的完整性，解决了神经网络过拟合问题，但该风险评估体系因素集较少且依赖专家评分，评估过程和网络设计过于复杂适用性不强；李森宇 [7] 等人使用改进的布谷鸟算法对BP神经网络进行优化并应用于信息安全风险评估，以提高信息系统风险预测的准确率；但后续没有对风险因素进行分析，且网络时间消耗大容易陷入局部最优解，不利于后续的风险分析和管理。

针对上述的问题，本文利用量子粒子群算法在求解局部最优解的基础上求全局最优解的优势用于优化BP神经网络并将此引入到风险评估中，提出基于量子粒子群优化BP神经网络的云平台信息系统安全风险分析模型。首先，根据云平台虚拟化、集成度高以及基础架构复杂等特性，以云平台信息系统作为评估对象，构建基于信息系统的云平台风险分析模型；其次，利用量子理论的相干性与对大数据量的未知信息处理能力对风险因素值求解最优初始权值和阈值 [8] [9]；最后，将风险因素作为输入值进行网络训练输出风险值，再对风险进行单因素敏感度分析得出风险管理策略。

2. 量子粒子群优化BP神经网络

2.1. 量子粒子群算法

在量子理论中，薛定谔方程描述了微观粒子的状态随时间变化的规律，其解为波函数，而波函数描述了系统所有粒子的演化过程，则粒子行为存在于系统行为演化的波函数中。根据粒子群的基本收敛性质以及量子力学中的相关理论，2004年Sun等人提出基于势阱模型的量子行为粒子群优化算法，并针对波函数的特征长度的特性，设计一种基于全局水平的参数控制方法，提出量子行为粒子群优化算法 [10] (Quantum-behaved Particle Swarm Optimization, QPSO)。

在量子粒子群算法中，粒子有局部最优解和全局最优解，且粒子的搜索空间和求解空间性质不同。波函数描述粒子在搜索空间量子化的状态并规定粒子在势阱中的搜索范围，公式如下：

$\Psi \left(x\right)=\frac{1}{\sqrt{L}}\exp \left(-\Vert P-X\Vert /L\right)$ (1)

粒子X的位置进化方程为：

$X\left(t+1\right)=P\pm \alpha \ast \left|mbest-X\left(t\right)\right|\ast \ln \left(1/u\right)$ (2)

式中 $\alpha$ 为控制参数，决定粒子的进化位置和下一次搜索范围；u为(0,1)上的均匀分布；P是粒子的局部最好位置，每一维的第i个粒子位置X_i依概率收敛于P_i；t为迭代次数，及粒子群位置更新次数；L为 $\delta$ 势阱的特征长度，是控制粒子搜索范围的重要参量，其进化方程为：

$L\left(t+1\right)=2\ast \alpha \ast \left|mbest-X\left(t\right)\right|$ (3)

mbest为所有粒子的局部最好位置平均值，是此次进化粒子的全局最优位置。mbest的表达式如式4所示，式中M为粒子个数。

$mbest={\displaystyle \underset{i=1}{\overset{M}{\sum }}{P}_i/M}$ (4)

2.2. QPSO-BP模型

BP神经网络为有监督学习，通过误差信号反向传播修正权值，传统BP神经网络训练在之前会随机选取初始权值再进行网络训练，并基于梯度下降法，使实际输出值与期望输出值之间的误差平方和最小化；然而随机选取初始值会降低BP神经网络训练效率，降低迭代速率，造成学习收敛速度慢、陷入局部最优等问题。

针对传统BP神经网络的局限性，国内外很多学者采用免疫算法、遗传算法等仿生算法对BP神经网络进行优化 [11] [12] [13] [14]，这些优化方法参数设置多并且易陷入局部最小值；然而，QPSO是一种全局搜索的仿生算法，控制参数较少，有较强的鲁棒性。因此，本文采用QPSO优化BP神经网络，选取最优的初始权值和阈值，以提高网络的全局寻优能力和收敛速率。量子粒子群优化BP神经网络模型如图1所示，算法流程图如图2所示。

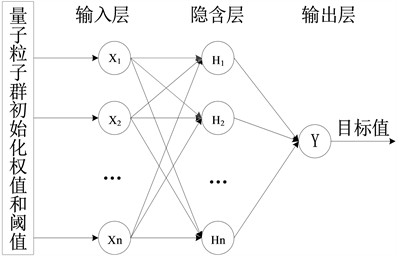
Figure 1. Quantum particle swarm optimization BP neural network model

图1. 量子粒子群优化BP神经网络模型

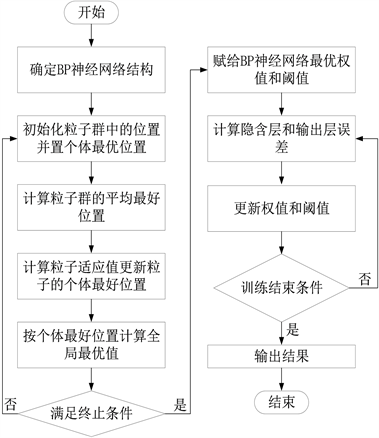
Figure 2. Quantum particle swarm optimization BP neural network algorithm flow

图2. 量子粒子群优化BP神经网络算法流程

3. 基于云平台信息系统的风险分析模型

3.1. 云平台信息系统安全风险因素模型

云平台有IaaS、PaaS和SaaS三层云服务，每层都有相应的技术来支持该层的服务，可构建相应的独立“云”，也可基于下一层的“云平台”提供服务，每种“云”可直接提供给终端用户，也可以只用于支撑上层的服务。相对于其它两种底层服务形式，SaaS提供最为集成化的功能，可以用于某些特定功能的应用，是云租户最常使用的云服务租用模式。与此同时，对于用户的个人数据信息的控制度也是最高的，在遭受到了安全风险的威胁时，面临着数据大量泄漏的危险。因此，以网络信息系统资产为切入点，主要针对云平台的SaaS层进行安全风险的评估与分析。

云平台由于自身架构过于复杂，较多的依赖于底层的支撑技术(例如分布式计算、虚拟化技术以及网络通信技术等)，造成一系列安全难题，国内学者针对此难题构建云计算环境的安全检查与评估指标体系 [15]。因此，根据云平台信息安全资产，从物理安全、云网络安全、云虚拟化安全、云应用安全以及云数据安全五部分对系统进行风险的评估和分析，具体可分别：机房设施(r₁)、基础设备(r₂)、云网络加密措施(r₃)、云网络设备安全(r₄)、云网络访问控制(r₅)、云监视器(r₆)、云管理平台(r₇)、安全攻击及防御(r₈)、云应用隐私保护(r₉)、云数据安全存储(r₁₀)、云数据安全共享(r₁₁)，云数据安全加密(r₁₂)，构建云平台信息系统安全风险因素模型，如图3所示。

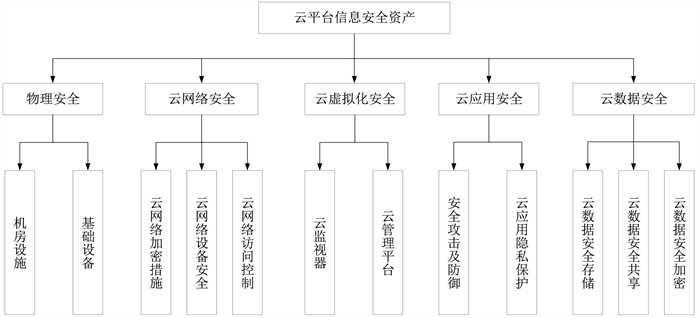
Figure 3. Cloud platform information system security risk factor model

图3. 云平台信息系统安全风险因素模型

根据国家安全等级保护的安全控制项的要求，通过对云平台系统的信息系统安全配置项进行检查，并对调查数据进行统计分析，完成对云平台安全风险因素的量化，以实现对于风险的定量分析。传统风险分析模型为 $R=f\left(A,T,V\right)$ ，其中A为资产，T表示威胁，V表示脆弱性。根据QPSO-BP算法思想将信息系统风险分析模型抽象为：

$R=f\left[Q\left(X\right)\right]$ (5)

式中 $X=\left(X_1,\cdots ,X_n\right)$ 表示各单位风险值向量， $X_n={\left(r_1,r_1,\cdots ,r_{12}\right)}^T$ 是根据现场检测得到风险因素的风险值；Q表示量子粒子群算法；f表示BP算法；R表示经QPSO-BP映射的系统风险值。

3.2. 云平台信息系统安全风险模型训练过程

云平台信息系统安全风险因素模型为三层的逻辑结构，而神经网络模型的三层网络模型中隐含层能拟合任意函数。运用量子粒子群BP神经网络对风险值预测，以云平台信息系统的风险因素值作为模型的输入，通过量子粒子群算法寻找BP网络的初始最优权值和阈值，最终输出值为信息系统的风险值。具体步骤如下：

步骤1：信息系统风险因素特征参数初始化，将对系统检查得到的资产风险实值样本进行归一化处理后，得到粒子群算法的输入值。

步骤2：粒子群初始化，将风险因素值作为输入粒子，设量子粒子群算法迭代次数为t，置t = 0，种群数为12，设粒子的初始位置 $X_i\left(0\right)$ ，且 $P_i\left(0\right)=X_i\left(0\right)$ 。

步骤3：根据式(4)计算粒子群的mbest值和粒子i的适应值X_i(t)；若X_i(t)优于 $X_i\left(t-1\right)$ ，则 $P_i\left(t\right)=X_i\left(t\right)$ ，否则 $P_i\left(T\right)=P_i\left(t-1\right)$ 。

步骤4：将P_i(t)与全局最优位置 $D\left(t-\text{1}\right)$ 比较，若P_i(t)优于 $D\left(t-\text{1}\right)$ ，则置 $D\left(t\right)=P_i\left(t\right)$ ；否则 $D\left(t\right)=D\left(t-\text{1}\right)$ 。

步骤5：根据公式(2)计算粒子的新位置。

步骤6：如果 $t<t_{\max }$ ，则 $t=t+1$ ，转入步骤3，否则转入步骤7。

步骤7：将QPSO算法得到的结果作为BP神经网络的初始权值和阈值，进行网络训练，计算输出误差值。

步骤8：根据误差，调整网络权值和阈值，进入下一次训练。

步骤9：若达到最大迭代次数或者预设精度则输出结果，否则转入步骤8。

3.3. 云平信息系统安全风险分析

基于量子粒子群优化BP神经网络的云平台信息系统安全风险分析的过程如下：

步骤1：将待分析的云平台系统风险数据归一化处理，将归一化后的样本特征参数作为QPSO算法的初始粒子值。

步骤2：将QPSO的输出值作为网络的初始权值和阈值，进行网络训练得出风险值。根据样本的误差均值 $\bar{e}=\frac{1}{n}{\displaystyle \underset{i=1}{\overset{n}{\sum }}{e}_i}$ ，标准差 $\sigma =\sqrt{\frac{1}{n}{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\left(e_i-\bar{e}\right)}^2}}$ ，调整网络参数，使网络输出值误差最小。

步骤3：根据网络输出值，计算第i个风险因素敏感度 $S_i=\left|{R^{\prime }}_i-R_i\right|$ ，对云平台信息系统的安全因素做风险分析。云平台信息系统安全风险分析流程如图4所示。

Figure 4. Cloud platform information system security risk analysis process

图4. 云平台信息系统安全风险分析流程

4. 仿真实验

仿真使用Windows10和Matlab R2019b作为测试环境。数据源于对多家单位的云平台信息系统安全调查，以信息资产的保密性、完整性和可用性赋值为原始数据，根据影响程度对风险因素预处理得样本数据，归一化处理后的样本数据如表1所示。取前30组为训练样本后12组为测试样本。根据测试数据分析模型结构为12-5-1，设最大迭代步数为1000，误差精度为0.0001。

在相同条件下，分别通过QPSO-BP、粒子群优化BP神经网络(PSO-BP)、遗传算法优化BP神经网络(GA-BP)进行样本训练，根据实验可知，QPSO-BP算法的收敛速度和预测拟合度明显优于另外两种网络。QPSO-BP性能曲线图5所示、PSO-BP性能曲线图6所示、GA-BP性能曲线图7所示。

Table 1. Normalized sample data

表1. 归一化样本数据

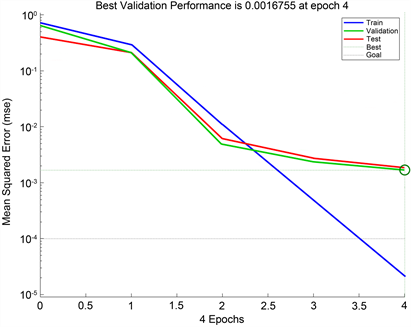
Figure 5. QPSO-BP performance curve

图5. QPSO-BP性能曲线

Figure 6. PSO-BP performance curve

图6. PSO-BP性能曲线

Figure 7. GA-BP performance curve

图7. GA-BP性能曲线

三种算法的预测结果比较如图8所示。实验结果表明，这三种算法都能对风险进行有效的预测，GA-BP迭代次数多且达不到预测效果，PSO-BP迭代次数少但拟合程度不够，QPSO-BP则表现出良好的性能，迭代次数少网络效率高且能更准确进行预测，误差均值和标准差均优于另外两种网络，算法误差对比分析如表2所示。因此，QPSO-BP预测算法更适用于云平台安全风险预测。

Figure 8. Comparison of test results

图8. 测试结果对比

Table 2. Network output risk error

表2. 网络输出风险误差

根据大小将风险值划分为五个等级，每个等级相应的给出风险评价，风险等级划分和评价如表3所示。计算出某一单位的风险值后，进行风险因素敏感度分析，即分析当某一风险因素出现波动时对系统风险造成的影响程度。以单位X₁为例对其进行风险敏感度分析；首先采用控制变量法计算单位X₁每个风险因素波动±10%后的变化值；再根据变化后的风险因素值预测风险值；最后分析云平台信息系统风险因素变化后的风险值波动情况如图9所示；由图知风险因素r₁₁变化后，风险值相较于原来风险波动最大；风险因素r₁₀变化后，对系统风险没有太大影响。

Table 3. Classification of cloud platform risk value levels

表3. 云平台风险值等级划分

Figure 9. Risk wave after risk factors change

图9. 风险因素变化后的风险波动

风险因素敏感度计算结果如表4所示，表中列出风险因素变化后的值、风险因素变化后的预测风险值以及风险敏感度。由风险因素敏感度分析得，X₁单位的风险因素的敏感度为0.0011和0.0009，相较于其他风险敏感度其值最小，则在本系统中风险因素r₁₀对系统风险影响最小；而风险因素r₁₁的敏感度为对0.0060和−0.0087，相较于其他因素其敏感度值波动较大，因此对系统风险值影响也较大，在该系统数据共享时加强数据的保护，避免敏感数据泄露和篡改等，应立即采取措施对数据进行加密管理和安全维护以规避风险。

Table 4. Sensitivity analysis of various risk factors of cloud platform

表4. 云平台各风险因素敏感度分析

5. 结论

通过对云平台安全架构的理论分析，构建基于云平台信息系统的风险分析模型，该模型以信息系统作为评估对象，利用QPSO-BP算法有效地解决网络局部最优问题，实现对云平台风险的预测，再对高风险系统进行风险因素敏感度分析，为有效地转移风险提供了相应的理论依据。实验表明，QPSO-BP神经网络适用于对云平台信息系统的安全风险值预测，实现对网络可调参数的更新，提高网络的收敛速率和未知风险的预测精度。通过分析各因素对风险值的影响，能更精准地对云平台信息系统风险进行管理，提高风险管理效率，为云平台信息系统风险分析提供一条新途径。

基金项目

国家社会科学基金资助项目[19BZX035]。