100 krpm~10 kW高速永磁电机转子系统的设计与校核研究

A Study on Design and Check for a Rotor System of a 100 krpm~10 kW High-Speed Permanent Magnet Motor

摘要: 本文研究的目的是开发一台额定功率为10 kW、最高转速为100 krpm的燃料电池空压机用高速永磁同步电机。针对永磁电机在超高转速下存在的离心应力过大导致永磁体拉伸变形失磁，以及细长转子在高速下容易发生扭转共振问题，本文重点研究高速转子系统的设计与校核。通过有限元分析研究了护套过盈量和厚度对转子部件应力应变的影响，确定了永磁体与护套之间的最佳过盈量与保护套厚度。转子系统的高速模态分析结果表明，转子系统的一、二阶临界转速远大于电机的最高工作转速，设计的电机转子系统在高速运行时不会发生扭转共振现象。

Abstract: The purpose of this paper is to develop a high-speed permanent magnet synchronous motor for a fuel cell air compressor with a rated 10 kW, maximum speed of 100,000 rpm. Aiming at the excessive centrifugal stress of permanent magnet motor at ultra-high speed, the permanent magnet tensile magnetization deformation and the torsion resonance of slender rotor at high speed, this paper focuses on the design and calibration of high-speed rotor system. The effect of the sheath surplus and thickness on the stress strain of the rotor component is studied by finite element analysis, and the optimal surplus and the sheath thickness between the permanent magnet and the sheath are determined. The results of high speed modal analysis of the rotor system show that the first and second critical speeds of the rotor system are much greater than the highest operating speed of the motor, designed motor rotor system will not have torsional resonance phenomenon at high speed.

1. 引言

燃料电池作为一种新能源技术，逐渐成为主流的汽车动力源，其中，空压机是决定其效率和成本的重要部件。目前，空压机存在与驱动电机的最高工作效率点不匹配导致系统效率不高的问题，所以高速电机的设计逐渐受到国际电工领域的重视，在电机设计的过程中，转子动力学问题是其技术难点之一，电机高速旋转时转子系统受到巨大的离心力与电磁力，转子易出现变形失磁与共振 [1]。因此近些年来高速永磁电机转子系统的设计受到了国内外学者广泛的关注。

B Riemer，M Lemann [2] 等人对一台10 kW的高速永磁电机进行转子结构强度设计。江苏大学的张涛、孙晓东 [3] 等人分别使用有限元法和解析法对高速电机的转子强度进行分析，确保电机在最高转速运行时拥有足够的机械强度。李振平 [4] 等人基于有限元分析和解析法，对一台最高转速为72,000 r/min的永磁电机，分析转子结构强度在永磁体与护套不同过盈量下的变化。沈阳工业大学的王凤翔 [5] 等人对转子强度与转子临界转速的仿真分析进行了多方面的研究，提供了大量的理论指导。

本文对电机转子的结构强度进行理论分析，基于Abaqus分析转子在不同条件下的冯米塞斯应力变化以及在不同转速范围下的最大变形量，验证其刚度是否符合要求。最终，对整个转子系统进行模态分析，计算其在各阶固有振动频率下对应的临界转速，得出设计的高速永磁电机转子系统满足转速需求。

2. 转子系统机械设计考虑与校核要求

2.1. 永磁体与护套之间的过盈量

表贴式永磁体和护套之间的过盈装配如图1所示，其中 $p_s$ 为施加在护套表面的预压力(Pa)； $r_{eo}$ 为护套外半径(m)； $r_{ei}$ 为护套内半径(m)； $r_{mo}$ 为永磁体外半径(m)； $r_{mi}$ 为永磁体内半径(m)。

永磁体和护套之间的过盈量大小对两者之间的静态接触应力和高速下的离心力有重大影响 [6]。过盈量选取过小，永磁体抗压特性不能合理利用，高速条件下永磁体的退磁风险增大；过盈量选取过大，永磁体的内部结构可能会出现永久性损伤。因此，过盈量的选取应结合高速永磁电机的具体结构参数，过盈量的计算公式为：

静止状态下的过盈量：

${\delta }_s=r_{mo}-r_{ei}$ (1.1)

旋转状态下的过盈量：

$u=Ar+\frac{B}{r}-\frac{\rho \left(1-v^2\right){\omega }^2{r}^3}{8E}$ (1.2)

$A=\frac{\left(3+v\right)\left(1-v\right)\left(r^2+r^2\right)\rho {\omega }^2}{8E}$ (1.3)

$B=\frac{\left(3+v\right)\left(1-v\right)r^2{r}^2\rho {\omega }^2}{8E}$ (1.4)

将相关参数代入分别求旋转下护套的位移量 $u_{d,ei}$ 与永磁体的位移量 $u_{d,mo}$，所以有相对位移量：

$\Delta {\delta }_d=u_{d,ei}-u_{d,mo}$ (1.5)

将计算结果，带入至公式(1.1)中便可以计算出永磁体与保护套在旋转下的过盈量：

${\delta }_d={\delta }_s-\Delta {\delta }_d$ (1.6)

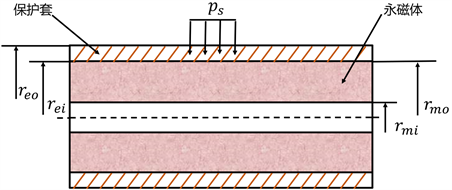
Figure 1. Assembly diagram of permanent magnet and sheath

图1. 永磁体与护套装配示意图

2.2. 永磁体与护套之间的应力应变理论

在转子中，护套与永磁体之间的安装方式为过盈配合 [7]，机械设计约束如下：

1) 永磁体与护套中的最大应力不超过其许用应力。

2) 永磁体与护套之间的接触压力大到足够传递电磁扭矩。

转子永磁体受接触压力 $P_c$ 和离心力作用，本文设计不考虑电磁力，因为电磁力与高速机器的机械载荷相比相当小。永磁体最大拉伸应力为：

${\sigma }_{PM,\max }={\sigma }_{PM,\omega }+{\sigma }_{PM,\rho }$ (1.7)

其中， ${\sigma }_{PM,\max }$ 为永磁体中的最大拉伸应力， ${\sigma }_{PM,\omega }$ 来自离心力， ${\sigma }_{PM,\rho }$ 来自永磁体与护套之间的接触压力 $p_c$，二者均可通过计算求得。

永磁体的应力极限值为：

${\sigma }_{PM，\max }\le \left[{\sigma }_{\text{PM}}\right]$ (1.8)

其中 $\left[{\sigma }_{PM}\right]$ 是永磁体的拉伸许用应力，护套中的冯–米塞斯应力计算公式：

${\sigma }_{Sleeve}=\sqrt{\frac{1}{2}\left[{\left({\sigma }_{S,\max }-{\tau }_{S,\max }\right)}^2+{\sigma }_{S,\max }^2+{\tau }_{S,\max }^2\right]}$ (1.9)

其中， ${\sigma }_{Sleeve}$ 为护套中的最大弯曲应力， ${\sigma }_{S,\max }$ 和 ${\tau }_{S,\max }$ 分别为护套中最大的径向应力和切向应力，两者都位于护套内部表面。均可通过公式求得。

3. 转子系统的离心应变分析与设计

有限元分析方法在模型精确的前提下，对转子系统应力分析更加符合实际情况，结果也更加准确 [8]。本文采用Abaqus中的静力学模块对不同保护套厚度、不同装配过盈量下的转子强度展开研究。

3.1. 过盈量对转子应力的影响

电机的转子结构为表贴式，考虑到高速电机转子对散热的要求较高，护套材料选择铝合金材料，安装采用合理的过盈配合。对于铝合金材料的护套，过盈量通常在0.06~0.14 mm中进行选取，为了研究护套与永磁体所受等效应力范围随过盈量大小的变化趋势并确定具体值，基于Abaqus中结构静力学模块对转速为100,000 r/min，不同过盈量下的永磁体和护套间的等效应力进行仿真分析，最终结果见表1。

Table 1. Calculation results of equivalent stress of permanent magnet and sheath under different interference

表1. 不同过盈量下的永磁体、护套等效应力计算结果

分析表中数据可知，永磁体与保护套之间的过盈量增大，永磁体、护套所受等效应力的范围也随之增大，永磁体在过盈量0.06~0.14 mm下的最小等效应力，由56.46 MPa增大至61.32 MPa；最大等效应力由99.03 MPa增至110.34 MPa，总体变化范围较小。由于铝合金护套材料属于弹性材料，因此在过盈量发生变化时，保护套的等效应力变化范围更大，具体如图2所示。

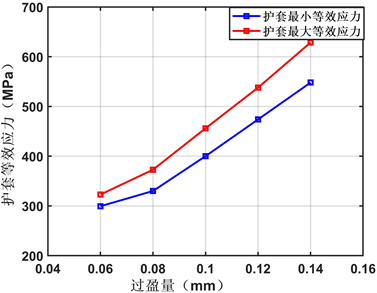
Figure 2. Variation of equivalent stress of sheath under different interference

图2. 不同过盈量下的护套等效应力变化

分析图2得，在过盈量为0.14 mm时，护套的两个等效应力的最大值均在屈服强度范围内，但护套所受的最大等效应力达到628.6 MPa，接近合金钢的屈服强度630 MPa，不利于保证转子强度。最终，在保证转子强度的前提下，尽可能多的消除离心力作用，将过盈量大小设置为0.12 mm。

3.2. 保护套厚度对转子应力的影响

对于表贴式高速永磁电机而言，永磁体保护套的厚度也是转子系统设计中重要一环。护套厚度对永磁体与护套的等效应力有着显著的影响 [9]，文章第一部分通过公式深入分析铝合金护套厚度对应力应变的影响特征，在确定静态过盈量为0.12 mm的设计前提下，再基于Abaqus中的静力学模块对不同保护套厚度下的转子强度进行应力分析，进行有针对性的优化护套厚度，得到最优的应力应变特征下对应的最佳护套厚度，结果如表2所示。

Table 2. Calculation results of equivalent stress of permanent magnet and sheath with different sheath thickness

表2. 不同护套厚度的永磁体、护套等效应力计算结果

通过表2中的仿真结果得，永磁体与护套之间的接触压力不变时，随着保护套厚度在2.0 mm~4.0 mm范围内不断增加，永磁体与保护套的等效应力均不断减小，整理得图3。

Figure 3. Equivalent stress variation of permanent magnet and protective sleeve under different sheath thickness

图3. 永磁体与保护套在不同护套厚度下的等效应力变化

分析上图得，随着保护套厚度增加，虽然永磁体与护套的等效应力均减小，但其减小的趋势不断减弱，其中永磁体的应力变化并不明显，而护套厚度过大时，护套质量变大，离心力增大，浪费护套的材料；护套越厚，护套上的涡流损失增大，发出的热量增多，物理气隙不变的条件下散热性差。

对比与分析铝合金护套不同厚度下的等效应力分布，结合传热，涡流损耗这几方面 [10] 综合考虑确定铝合金护套厚度的最优解为2 mm，根据过盈量与保护套厚度尺寸大小，在Abaqus中对转子系统的初始三维模型进行修正并重新校核其强度要求。最终，得到冯米塞斯应力分布如图4。

Figure 4. Von Mises stress distribution of rotor system (unit: MPa)

图4. 转子系统的冯米塞斯应力分布(单位：MPa)

由分析结果得可知，在考虑过盈配合后，转子系统的最大冯米塞斯应力达到537.9 MPa，远远小于保护套的屈服强度，故此转子的最新结构尺寸满足机械强度要求。

4. 高速转子系统的扭转共振分析

高速永磁电机在转速达到100 krpm条件下运作时，转子本身的动力学特征作为一项重要的性能指标，其振动与变形需要深入思考，从离心力角度设计转子时需要考虑转子的细长结构问题，而细长设计又存在扭转共振问题 [11]。所以在完成细长杆转子的设计后，需要对转子的动力学进行仿真分析，验证其刚度能否满足运动强度以及避免共振。现基于Abaqus对电机转子变形量和转子系统的前四阶固有频率进行仿真计算并对结果进行刚度分析与模态分析。

4.1. 转子系统的刚度分析

在不影响仿真结果精确度的前提下，为了减少仿真计算的时间，对转子系统的非关键部件进行简化处理，根据确定的最佳过盈量与保护套厚度以及其它转子尺寸参数，建立3D模型并赋予材料属性以及重力、转速等载荷条件，完成对转子系统的网格剖分。最终计算出转子系统在不同转速范围下的最大变形量，结果如图5示。

Figure 5. Maximum deformation of rotor at different speeds

图5. 不同转速下的转子最大变形量

分析上图可知，随着电机转速不断增大，转子系统的最大变形量也不断增加，且正比于转速平方。当电机转速达到最高值时，转子系统的最大变形量达到最大值，此时有转子系统的总体位移结果图6。

Figure 6. Displacement nephogram of rotor system (unit: mm)

图6. 转子系统的位移云图(单位：mm)

由上图得知，转子系统的最大变形量大致位于中心区域，大小为0.154 mm。对于高速永磁电机而言，电机转轴所能允许的最大变形量应小于气隙长度10% [12]。当前电机的气隙长度大小设置为5.64 mm，所能允许的最大变形量为0.564 mm，大于当前转子系统的最大变形量0.154 mm。能够满足高速永磁电机刚度的设计要求。

4.2. 转子系统的模态分析

高速电机转子振动的强弱不仅受转子刚度的影响，还受转子临界转速的影响，转子结构在制造的过程中总会存在细微的误差，转子各微段的质心一般对中心旋转轴线有微小的偏离，转子在高速旋转时，这些偏离造成的离心力会使转子产生横向振动。这种振动在某些转速上显得异常强烈，这些转速称为临界转速 [13]。因此，为了避免转子系统发生扭转振动现象，转子的临界转速分析同样值得关注。

转子临界转速的具体数值通常由转子的固有振动频率决定，故在高速永磁电机的设计过程中，需要对转子系统进行模态分析，根据其固有频率计算出转子在不同阶数下的临界转速。对于刚性转子而言，其工作的转速需要低于一阶临界转速0.75倍才可以避免共振 [14]。基于Abaqus对转子系统进行模态分析，得到刚性转子在前四阶的固有频率和振型云图7。

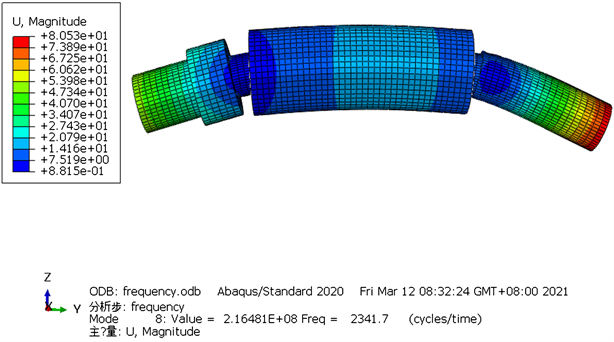
Figure 7. Nephogram of first four natural frequencies and vibration modes of rotor (unit: mm)

图7. 转子前四阶固有频率振型云图(单位：mm)

由图7可知，转子前四阶的具体固有频率值分别为2340.5 Hz、2341.7 Hz、4085.7 Hz和4088.3 Hz。结合固有频率与临界转速的计算公式：

$n_i=\frac{60\cdot {\omega }_i}{2\text{π}};f_i=\frac{{\omega }_i}{2\text{π}}$

式中， ${\omega }_i$ 为转子角速度(rad/s)， $n_i$ 为转子临界转速(r/min)， $f_i$ 为转子固有频率(Hz)。最终通过转换计算出转子每一阶固有频率对应的临界转速，见表3。

Table 3. Rotor natural frequency and critical speed

表3. 转子固有频率与临界转速

由表得知，电机转子系统的一阶临界转速达到140,430 r/min，其0.75倍为105,322.5 r/min，大于电机的最高转速100 krpm。所以电机在0~100 krpm转速范围内运行时不会发生共振现象，转子系统符合设计要求。

5. 结论

本文针对一台表贴式100 krpm~10 kW高速永磁电机，设计了较为完整的且能够满足强度需求的转子系统，同时研究了转子机械性能以及转子动力学特性随过盈量以及护套厚度的变化规律。

1) 首先，分析了护套与永磁体所受等效应力范围随过盈量大小的变化规律，结果表明：过盈量选取的不同，永磁体与护套所受等效应力范围的变化趋势也不相同，永磁体总体变化较小，而护套变化趋势较大，这主要是是由于铝合金护套材料属于弹性材料。

2) 之后，考虑到转子机械强度的限制，以护套最大应力大于其许用应力以及护套和永磁体之间的接触力为约束条件，确定了满足强度要求的护套厚度。结果表明：护套厚度对永磁体与护套之间等效应力有较小的影响，永磁体变化并不明显，所以在设计护套的厚度时需要从传热，涡流损耗和应力应变这几个方面综合考虑确定最优解。

3) 最后，对优化后的转子系统进行动力学仿真分析，结果表明：转子系统在高速旋转时其最大变形量大致位于中心区域，可通过中心区域变形量的计算，判断转子能够满足刚度要求；针对细长设计存在扭转共振问题，可对转子系统进行高速旋转下的模态分析，比对其实际转速与临界转速的大小，本文设计的转子系统实际转速远远小于二阶临界转速，能够有效避免扭转共振问题。