二阶常微分方程边值问题的5点差分算法

doi:10.12677/ORF.2022.121006

期刊菜单

二阶常微分方程边值问题的5点差分算法
Five-Point Difference Algorithm for Second-Order Ordinary Differential Boundary Value Problems

DOI: 10.12677/ORF.2022.121006, PDF, HTML, XML, 下载: 299 浏览: 819
作者: 李明英：贵州大学数学与统计学院，贵州贵阳
关键词: 边值问题；五点差分格式；代数精度；广义Peano定理；Boundary Value Problem； Five-Point Difference Scheme； Algebraic Precision； Generalized Peano Theorem

摘要: 本文针对二阶线性常微分方程两点边值问题，通过具有最高代数精度的二阶导数的组合式近似，构造了具有最高阶精度的等步长的五点差分格式，并利用广义Peano定理给出了精度阶数。用构造的格式对多个算例编程计算，用Taylor展开方法对边界进行离散处理，并将计算结果与精确解比较。计算结果表明，所构造的差分格式达到了最高的八阶精度。

Abstract: In this paper, for the two-point boundary value problems of second-order linear ordinary differential equations, a five-point difference scheme with equal step is constructed by constructing a combined approximation of the second derivative with the highest algebraic precision, and the precision order is given by using the generalized Peano theorem. A lot of examples are calculated with program by the constructed scheme, applying respectively the Taylor expansion method to discrete the boundary. The numerical results are compared with the exact solutions and show that the constructed scheme achieves the highest order accuracy of eight.

文章引用：李明英. 二阶常微分方程边值问题的5点差分算法[J]. 运筹与模糊学, 2022, 12(1): 58-67. https://doi.org/10.12677/ORF.2022.121006

1. 引言

微分方程的边值问题指的是定解条件只在求解区域的边界上确定的微分方程的定解问题。常微分方程边值问题在数学和物理问题都起着重要的作用现阶段对于常微分方程边值问题的研究已经非常成熟和普遍。同时也取得艰深的成果。常微分方程的边值问题很少能求出它的解析解，目前能求出解析解的仅有少部分典型的方程，因此，有必要数值求解通过使用数值计算方法获得的数值解，该数值计算方法是其精确解的近似，并且该近似具有代数精度。我们的目标是找到代数精度达到最高阶的计算方法，同时保证计算量不会过大。其高精度的算法可大大提高计算效率，对问题的数值求解，特别是其大范围或高精度的求解益处明显。差分法在求解常微分边值问题方法中是很常见同时也是很重要的办法之一。

余爱晖 [1] 介绍了依据网格构造三点有限差分方法，并验证了该方法的收敛性。邹序焱 [2] 用差分格式可以得到三对角的系数矩阵，然后用追赶法求解，最后的到的二阶精度的数值解。差分法通过不断的改进，代数精度也在不断提高。郭晓晔 [3] 等人用差分法求解常微分方程边值问题常规的差商近似导数得到代数精度为二阶的。四阶精度的差分格式由刘明会 [4] 介绍的通过运用中心差分公式，得到四阶差分公式，最终的误差精度也为四阶的。周保民 [5] 用中心差分格式公式近似导数，并通过对边界条件的处理来提高数值解的精确度，不同的边界处理得到的精度不同(在边界附近的节点上用不同的差分格式代替非对称差分法、减小宽带法、矩阵多项式法得到的截断误差分别为三阶、四阶、六阶)大大提高了计算精度。

2. 广义Peano定理与差分法

二阶常微分方程一般形式为 $y^{″} (x) = f (x, y, y^{'}), a \leq x \leq b$ ，即线性情形可表示为

$y^{″} + g (x) y^{'} + h (x) y = f (x)$ (1.1)

其中， $g (x), h (x), f (x)$ 是已知函数。

计算过程中(1.1)的计算量相对较复杂，我们可以通过将(1.1)式乘以 $v (x)$ ， $v (x) = e^{\frac{1}{2} \int_{a}^{x} g (t) d t}$ ，便可以将二阶常微分方程边值问题(1.1)化简为形如(1.2)的式子：

$y^{″} + p (x) y = q (x)$ (1.2)

因此我们可以统一考虑(1.2)式的常微分方程。

仅考虑第一类边界条件，对应的二阶常微分方程边值问题为：

${\begin{cases} y^{″} + p (x) y = q (x), a \leq x \leq b \\ y (a) = α, y (b) = β \end{cases}$ (1.3)

2.1. 差分法

对上述(1.3)，在等步长的情况，将区间[a, b]划分为n等分，令 $h = (b - a) / n$ ， $x_{0} = α, x_{n} = β$ 则 $x_{i} = x_{0} + i h, i = 1, 2, \dots, n$ 。

有限差分方法：通过离散的方法将定解区间离散为网格式的节点，将连续变量函数离散为离散函数构成的线性方程组，典型的差分法是通过利用差商近似导数或者是积分插值形式来构造差分格式。将差分格式带入原方程组化简得到定解条件下的近似得线性方程组，解这个方程组就可以得到原问题在离散点的近似解。典型的差分法如下式所示：

$\begin{array}{l} y (x + h) = y (x) + h y^{'} (x) + \frac{h^{2}}{2!} y^{″} (x) + \frac{h^{3}}{3!} y^{‴} (x) + \dots \\ y (x - h) = y (x) - h y^{'} (x) + \frac{h^{2}}{2!} y^{″} (x) - \frac{h^{3}}{3!} y^{‴} (x) + \dots \\ y (x + h) + y (x - h) = 2 y (x) + h^{2} y^{″} (x) + \frac{h^{2}}{12} y^{4} (x) + \dots \\ y^{″} (x) = \frac{y (x + h) - 2 y (x) + y (x - h)}{2 h} + o (h^{2}) \end{array}$ (1.4)

用差商近似二阶导数 $y^{″} (x) \approx \frac{y (x + h) - 2 y (x) + y (x - h)}{2 h}$ 具有二阶精度的误差。

2.2. 广义Peano定理

定义(代数精度)：设 $I [f]$ 和 $Q [f]$ 均为f的线性泛函，若f为次数不超过m的多项式时，均有 $I [f] = Q [f]$ ，而 $I [x^{m +}^{1}] \neq Q [x^{m +}^{1}]$ ，则称近似公式 $I [f] \approx Q [f]$ (或 $R [f] = I [f] - Q [f] \approx 0$ )具有m次代数精度。

定理(广义Peano定理)：若 $R [f]$ 是线性泛函， $R [f] \approx 0$ 具有m次代数精度，则 $R [f] = R [e]$ ，其中 $e (x)$ 为 $f (x)$ 的任意m+1个节点 $x_{0}, x_{1}, x_{2}, \dots, x_{m}$ 的插值多项式的余项。

由插值多项式的理论可知， $e (x)$ 可表示为

$e (x) = \frac{f^{(m + 1)} (ξ)}{(m + 1)!} (x - x_{0}) \dots (x - x_{n})$ (1.5)

$x_{0}, x_{1}, \dots, x_{m}$ 是区间[a, b]上的任意点，且 $ε$ 在 $x_{0}, x_{1}, x_{2}, \dots, x_{m}$ 与x之间。

设L_m(x)是满足定理条件的m次插值多项式，则 $f (x) = L_{m} (x) + e (x)$ ，即可得到 $R [f (x)] = R [L_{m} (x) + e (x)] = R [L_{m} (x)] + R [e (x)] = R [e (x)]$ 。

3. 常微分方程边值问题的五点差分格式

在这一部分，本文对于(1.3)式类型的常微分方程边值问题构造五点差分格式，展开了下述研究。

3.1. 推导(1.3)式的高精度的五点差分格式

过程如下：欲使

$R [y] = {a_{0} y^{″} |}_{x_{k - 2}} + {a_{1} y^{″} |}_{x_{k - 1}} + \dots + {a_{4} y^{″} |}_{x_{k + 2}} - (b_{0} y (x_{k - 2}) + b_{1} y (x_{k - 1}) + \dots + b_{4} y (x_{k + 2})) \approx 0$ (2.1)

具有最高阶精度，就要求不全为零的系数 ${a_{i}, b_{i}}$ ，使得 $R [1] = 0, R [x] = 0, \dots, R [x^{m}] = 0$ 对尽可能大的m成立。式子中有十个未知数，但独立的只有九个，所以只需要九个方程就能求解出系数。

将 $y = 1, y = x, y = x^{2}, y = x^{3}, \dots, y = x^{8}$ 带入(2.1)则可以得到九个方程。因为要求系数 ${a_{i}, b_{i}}$ 不全为零，可先取定 $a_{2} = 1$ ，即可解出系数 $a_{0}, a_{1}, \dots, a_{4}, b_{0}, \dots, b_{4}$ 。

为了计算方便，令 $x_{k - 2} = - 2 h, x_{k - 1} = - h, x_{k} = 0, x_{k + 1} = h, x_{k + 2} = 2 h$

则有

$R [x^{k}] = 0$ $(k = 0, 1, 2, \dots, 8)$ (2.2)

得到方程为：

${\begin{cases} b_{0} + b_{1} + b_{2} + b_{3} + b_{4} = 0 \\ - 2 b_{0} - b_{1} + b_{3} + 2 b_{4} = 0 \\ 2 (a_{0} + a_{1} + a_{2} + a_{3} + a_{4}) - (4 b_{0} + b_{1} + b_{3} + 4 b_{4}) h^{2} = 0 \\ 6 (- 2 a_{0} - a_{1} + a_{3} + 2 a_{4}) - (- 8 b_{0} - b_{1} + b_{3} + 8 b_{4}) h^{2} = 0 \\ 12 (4 a_{0} + a_{1} + a_{3} + 4 a_{4}) - (16 b_{0} + b_{1} + b_{3} + 16 b_{4}) h^{2} = 0 \\ 20 (- 8 a_{0} - a_{1} + a_{3} + 8 a_{4}) - (- 32 b_{0} + b_{1} + b_{3} + 32 b_{4}) h^{2} = 0 \\ 30 (16 a_{0} + a_{1} + a_{3} + 16 a_{4}) - (64 b_{0} + b_{1} + b_{3} + 64 b_{4}) h^{2} = 0 \\ 42 (- 32 a_{0} - a_{1} + a_{3} + 32 a_{4}) - (- 128 b_{0} - b_{1} + b_{3} + 128 b_{4}) h^{2} = 0 \\ 56 (64 a_{0} + a_{1} + a_{3} + 64 a_{4}) - (256 b_{0} + b_{1} + b_{3} + 256 b_{4}) h^{2} = 0 \end{cases}$ (2.3)

通过matlab符号计算求解得(取 $a_{2} = 1$ )：

$\begin{array}{l} a_{0} = \frac{23}{2358}, a_{1} = \frac{344}{1179}, a_{2} = 1, a_{3} = \frac{344}{1179}, a_{4} = \frac{23}{2358} \\ b_{0} = \frac{155}{786 h^{2}}, b_{1} = \frac{320}{393 h^{2}}, b_{2} = - \frac{265}{131 h^{2}}, b_{3} = \frac{320}{393 h^{2}}, b_{4} = \frac{155}{786 h^{2}} \end{array}$

将系数代入(2.1)式，可验证 $R [x^{9}] = 0, R [x^{10}] \neq 0$ ，这样得出R[y]具有九次代数精度。

得到的五点差分格式如下：

$\begin{array}{l} \frac{{23 y^{″} |}_{x_{k - 2}} + {688 y^{″} |}_{x_{k - 1}} + {2358 y^{″} |}_{x_{k}} + {688 y^{″} |}_{x_{k + 1}} + {23 y^{″} |}_{x_{k + 2}}}{2358} \\ \approx \frac{155}{786 h^{2}} y (x_{k - 2}) + \frac{320}{393 h^{2}} y (x_{k - 1}) - \frac{256}{131 h^{2}} y (x_{k}) + \frac{320}{393 h^{2}} y (x_{k + 1}) + \frac{155}{786 h^{2}} y (x_{k + 2}) \end{array}$ (2.4)

3.2. 用差分格式求解

步骤：分别用所求解的系数与原常微分方程相乘，然后相加化简(合并同类项)再用所得的差分格式近似代换

${\begin{cases} a_{0} ({y^{″}}_{k - 2} + p_{k - 2} y_{k - 2}) = a_{0} q_{k - 2} \\ a_{1} ({y^{″}}_{k - 1} + p_{k - 1} y_{k - 1}) = a_{1} q_{k - 1} \\ a_{2} ({y^{″}}_{k} + p_{k} y_{k}) = a_{2} q_{k} \\ a_{3} ({y^{″}}_{k + 1} + p_{k + 1} y_{k + 1}) = a_{3} q_{k + 1} \\ a_{4} ({y^{″}}_{k + 2} + p_{k + 2} y_{k + 2}) = a_{4} q_{k + 2} \end{cases}$ (2.5)

$\begin{array}{l} (a_{0} {y^{″}}_{k - 2} + a_{1} {y^{″}}_{k - 1} + a_{2} {y^{″}}_{k} + a_{3} {y^{″}}_{k + 1} + a_{4} {y^{″}}_{k + 2}) \\ + (a_{0} p_{k - 2} y_{k - 2} + a_{1} p_{k - 1} y_{k - 1} + a_{2} p_{k} y_{k} + a_{3} p_{k + 1} y_{k + 1} + a_{4} p_{k + 2} y_{k + 2}) \\ = a_{0} q_{k - 2} + a_{1} q_{k - 1} + a_{2} q_{k} + a_{3} q_{k + 1} + a_{4} q_{k + 2} \end{array}$

将二阶导用差分格式近似代换后得：

$\begin{array}{l} (b_{0} y_{k - 2} + b_{1} y_{k - 1} + b_{2} y_{k} + b_{3} y_{k + 1} + b_{4} y_{k + 2}) \\ + (a_{0} p_{k - 2} y_{k - 2} + a_{1} p_{k - 1} y_{k - 1} + a_{2} p_{k} y_{k} + a_{3} p_{k + 1} y_{k + 1} + a_{4} p_{k + 2} y_{k + 2}) \\ = a_{0} q_{k - 2} + a_{1} q_{k - 1} + a_{2} q_{k} + a_{3} q_{k + 1} + a_{4} q_{k + 2} \end{array}$

带入计算系数 $k = 2, 3, 4, \dots, n - 2$ 得线性方程组用与求解离散近似解。

${\begin{cases} (\frac{320}{393} + \frac{344}{1179} p_{1} h^{2}) y_{1} + (- \frac{256}{131} + p_{2} h^{2}) y_{2} + (\frac{320}{393} + \frac{344}{1179} p_{3} h^{2}) y_{3} + (\frac{155}{786} + \frac{23}{2358} p_{4} h^{2}) y_{4} \\ = \frac{h^{2}}{2358} (23 q_{0} + 688 q_{1} + 2358 q_{2} + 688 q_{3} + 23 q_{4}) + (\frac{155}{786} + \frac{23}{2358} p_{0} h^{2}) y_{0} \\ (\frac{155}{786} + \frac{23}{2358} p_{1} h^{2}) y_{1} + (\frac{320}{393} + \frac{344}{1179} p_{2} h^{2}) y_{2} + (- \frac{256}{131} + p_{3} h^{2}) y_{3} + (\frac{320}{393} + \frac{344}{1179} p_{4} h^{2}) y_{4} \\ + (\frac{155}{786} + \frac{23}{2358} p_{5} h^{2}) y_{5} = \frac{h^{2}}{2358} (23 q_{1} + 688 q_{2} + 2358 q_{3} + 688 q_{4} + 23 q_{5}) \\ ⋮ \\ (\frac{155}{786} + \frac{23}{2358} p_{n - 5} h^{2}) y_{n - 5} + (\frac{320}{393} + \frac{344}{1179} p_{n - 4} h^{2}) y_{n - 4} + (- \frac{256}{131} + p_{n - 3} h^{2}) y_{n - 3} + (\frac{320}{393} + \frac{344}{1179} p_{n - 2} h^{2}) y_{n - 2} \\ + (\frac{155}{786} + \frac{23}{2358} p_{n - 1} h^{2}) y_{n - 1} = \frac{h^{2}}{2358} (23 q_{n - 5} + 688 q_{n - 4} + 2358 q_{n - 3} + 688 q_{n - 2} + 23 q_{n - 1}) \\ (\frac{155}{786} + \frac{23}{2358} p_{n - 4} h^{2}) y_{n - 4} + (\frac{320}{393} + \frac{344}{1179} p_{n - 3} h^{2}) y_{n - 3} + (- \frac{256}{131} + p_{n - 2} h^{2}) y_{n - 2} + (\frac{320}{393} + \frac{344}{1179} p_{n - 1} h^{2}) y_{n - 1} \\ + (\frac{155}{786} + \frac{23}{2358} p_{n} h^{2}) y_{n} = \frac{h^{2}}{2358} (23 q_{n - 4} + 688 q_{n - 3} + 2358 q_{n - 2} + 688 q_{n - 1} + 23 q_{n}) \end{cases}$

由线性方程组看到有n−3个方程组但有n−1个未知数，需要对边界进行处理。

3.3. Taylor展开处理边界条件

Taylor展开处理常微分方程边值问题的线性方程组的边界条件，提高数值解的计算精度方法除了差分格式我们还可以通过对边界条件的处理来提高代数精度。

过程：

由Taylor展开公式

$\begin{matrix} y_{0} = y (x_{1} - h) \\ = y (x_{1}) + y^{'} (x_{1}) (- h) + \frac{y^{″} (x_{1})}{2!} {(- h)}^{2} + \frac{y^{‴} (x_{1})}{3!} {(- h)}^{3} + \frac{y^{(4)} (x_{1})}{4} {(- h)}^{4} + \dots \end{matrix}$ (2.6)

$\begin{matrix} y_{2} = y (x_{1} + h) \\ = y (x_{1}) + y^{'} (x_{1}) h + \frac{y^{″} (x_{1})}{2!} h^{2} + \frac{y^{‴} (x_{1})}{3!} h^{3} + \frac{y^{(4)} (x_{1})}{4} h^{4} + \dots \end{matrix}$ (2.7)

将两式相加进行离散到具有四阶精度，与原常微分方程结合

$y_{0} + y_{2} = 2 y_{1} + y^{″} (x_{1}) h^{2} + \frac{y^{4} (x_{1})}{12} h^{4} + \dots$ (2.8)

$\begin{array}{l} y^{″} (x) + p (x) y = q (x) \\ y^{″} (x) = q (x) - p (x) y \end{array}$ $\begin{array}{l} y^{‴} (x) = q^{'} (x) - p^{'} (x) y - p (x) y^{'} (x) \\ y^{(4)} (x) = q^{″} (x) - p^{″} (x) y - 2 p^{'} (x) y^{'} - p (x) y^{″} (x) \end{array}$

将上式方程组结合化简，离散后可以得到我们想要的阶数的边值条件方程式

1) 四阶精度

上边界：

$(p (x) \times h^{2} - 2) y_{1} + y_{2} = q (x) \times h^{2} - y_{0}$ (2.9)

下边界：

$y_{n - 2} + (p (x) \times h^{2} - 2) y_{n - 1} = q (x) \times h^{2} - y_{n}$ (2.10)

2) 六阶精度(适用p(x)为常数)

上边界：

$y_{0} + y_{2} = (2 - p_{1} h^{2} + \frac{1}{12} {p^{″}}_{1} + p_{1}^{2}) y_{1} + q_{1} h^{2} + \frac{1}{12} {q^{″}}_{1} - 2 {p^{'}}_{1} {y^{'}}_{1} - p_{1} q_{1}$ (2.11)

下边界：

$y_{n - 2} + y_{n} = (2 - p_{n - 1} h^{2} + \frac{1}{12} {p^{″}}_{n - 1} + p_{n - 1}^{2}) y_{n - 1} + q_{n - 1} h^{2} + \frac{1}{12} {q^{″}}_{n - 1} - 2 {p^{'}}_{n - 1} {y^{'}}_{n - 1} - p_{n - 1} q_{n - 1}$ (2.12)

3) 八阶精度(适用于p(x)为常数)

上边界：

$(p_{1} h^{2} + \frac{h^{6}}{360} p_{1}^{3} - \frac{h^{4}}{12} p_{1}^{2} - 2) y_{1} + y_{2} = q_{1} h^{2} + \frac{h^{4}}{12} ({q^{″}}_{1} - p_{1} q_{1}) + \frac{h^{6}}{360} (q^{4} - p_{1} {q^{″}}_{1} + p_{1}^{2} q_{1}) - y_{0}$ (2.13)

下边界：

$y_{n - 2} + (p_{n - 1} h^{2} + \frac{h^{6}}{360} p_{n - 1}^{3} - \frac{h^{4}}{12} p_{n - 1}^{2} - 2) y_{n - 1} = q_{n - 1} h^{2} + \frac{h^{4}}{12} ({q^{″}}_{n - 1} - p_{n - 1} q_{n - 1}) + \frac{h^{6}}{360} (q^{4} - p_{n - 1} {q^{″}}_{n - 1} + p_{n - 1}^{2} q_{n - 1}) - y_{n}$ (2.14)

带入线性方程组中得到五对角的矩阵进行求解常微分方程边值问题。使用LU分解法，通过编程求解。

3.4. 差分格式的收敛性

由3.1节中 $x_{k - 2} = - 2 h, x_{k - 1} = - h, x_{k} = 0, x_{k + 1} = h, x_{k + 2} = 2 h$ 时，得到 $R [1], R [x], R [x^{2}], \dots, R [x^{8}]$ 都为0，但是

$\begin{matrix} R [x^{9}] = \frac{{23 y^{″} |}_{x_{k - 2}} + {688 y^{″} |}_{x_{k - 1}} + {2358 y^{″} |}_{x_{k}} + {688 y^{″} |}_{x_{k + 1}} + {23 y^{″} |}_{x_{k + 2}}}{2358} \\ - (\frac{155}{786 h^{2}} y (x_{k - 2}) + \frac{320}{393 h^{2}} y (x_{k - 1}) - \frac{265}{131 h^{2}} y (x_{k}) + \frac{320}{393 h^{2}} y (x_{k + 1}) + \frac{155}{786 h^{2}} y (x_{k + 2})) \\ = o ( h 8 ) \end{matrix}$

带入数据：

$R [x^{9}] = 0$

由系数具有对称性，我们可以推算的出 $R [x^{10}] \neq 0$ 所以差分格式(2.4)的代数精度m = 9。

由广义Peano定理，为了方便计算取双节点，得到：

$e (x) = \frac{y^{10} (ξ)}{10!} {(x - x_{0})}^{2} {(x - x_{1})}^{2} {(x - x_{2})}^{2} {(x - x_{3})}^{2} {(x - x_{4})}^{2}$

则截断误差为：

$R [f] = R [e] = a_{0} e^{″} (x_{0}) + \dots + a_{4} e^{″} (x_{4}) - (b_{0} e (x_{0}) + b_{1} e (x_{1}) + \dots + b_{4} e (x_{4}))$

将 $e (x)$ 带入化解得到式子如下：

$R [f] = \frac{871 y^{10} (ξ)}{47537280} h^{8}$

由于当 $h \to 0, R [f] \to 0$ 得出差分格式是收敛的。

4. 数值算例

例题1

${\begin{cases} y^{″} + x y = x \sin (x) - \sin (x) \\ y (0) = 0, y (π) = 0 \end{cases}$

我们能得出方程组的精确解为 $y = \sin (x)$ 。

为了方便比较我们取同一个常微分方程，边界处理通过Taylor展开到四阶精度取等步长 $h = b - a / n$ ，

n确定即h确定，其中 $e r r m = | y e - y t |$ ，ye为精确值yt为近似值，errm为最大误差 $R = \frac{e r r m}{h^{7}}$ 。

Table 1. Example 1 Error comparison under non-synchronous length

表1. 例题1不同步长下的误差对比

通过表1数据对比我们可以看到边界条件的精度对误差的影响很大对于近似解的误差精度，Taylor展开到了四阶精度，边界误差精度达10⁻¹⁰，得到的差分格式的最高阶精度为五阶。

通过图1可以看得边界为四阶Taylor展开的拟合程度良好。

例题2：

${\begin{cases} y^{″} - y = - 2 \sin (x) \\ y (0) = 0, y (π) = 0 \end{cases}$

可以解除其精确解为 $y = \sin (x)$ 。

根据3.3节介绍的Taylor展开处理边界条件到六阶精度进行计算对上述方程组进行离散求解，同样取等步长 $h = b - a / n$ ，n确定步长确定。 $e r r m = \max | y e - y t |$ ，ye为近似解，yt精确解，因此errm表示最

大误差，为 $R = \frac{e r r m}{h^{7}}$ 。

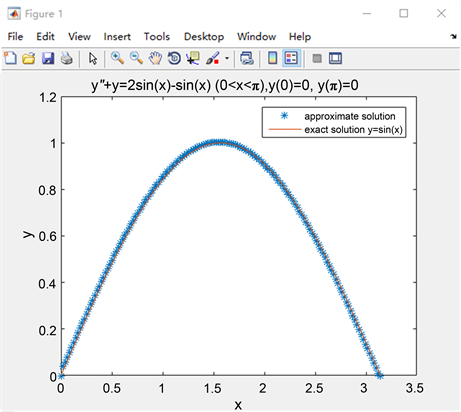
Figure 1. Example Problem 1 Comparison diagram of approximate solution and exact solution

图1. 例题1近似解与精确解对比图

Table 2. Example 2 Error comparison under non-synchronization length

表2. 例题2不同步长下的误差对比

从表2中数据分析我们得出同样的结论n越大误差越小R在0.002的上下波动，我们可以得到差分格式的最高精度为七阶。可以看到步长越小得到的误差越小，结果越精确。通过于上个例题进行对比我们可以看出边界条件的精度对数值解的代数精度还是具有影响，精度越高得到的数值解也更精确。

如图2，展示了近似值与精确值的拟合图像，近似解与精确解几乎重合，我们能更直观的看出近似解的精度。

例题3：

${\begin{cases} y^{″} - y = - 2 \sin (x), 0 \leq x \leq π \\ y (0) = 0, y (π) = 0 \end{cases}$

可以求出精确解为 $y = \sin (x)$ 。

根据3.3节介绍的Taylor展开处理边界差分方程组离散到八阶精度进行计算，对上述方程组进行离

散求解，取等步长 $h = \frac{b - a}{n}$ ，最大误差为 $e r r m = | y e - y n |$ ， $R = \frac{e r r m}{h^{8}}$ 。

Figure 2. Example 2 Comparison diagram of approximate solution and exact solution

图2. 例题2近似解与精确解对比图

从表3中的数据我们可以显然的看到当步长取相对较大时就已经能达到很小的误差，当n取到40时几乎已经达到双精度的上限，也就是近似值与精确值在无限接近了。从R的数值在减小我们可以确定差分格式的阶数至少为八阶精度。得到的这个结果还是很理想的。

Table 3. Example 3 Error comparison under non-synchronization length

表3. 例题3不同步长下的误差对比

从图3我们可以看出近似值的离散点和精确解的拟合情况是几乎完全重合的，这样我们也能看出五点差分格式求出的数值解的精确性很高。

5. 结论

本文讨论在第一类边值条件下求解常微分方程边值问题的五点差分格式，求解常微分方程边值问题的差分格式有多种，五点差分格式相对较简单，但是却能大大提高精度，解出离散线性方程组后需要对边界条件进行处理后才能求解，本文讨论了两种处理方法，由于得到的是特殊的五对角矩阵用LU分解 [6] 了解到计算量约为O (49n)然后推广的追赶法最终求得离散数值解。广义Peano定理同样适用于第二类边值和第三类边值条件。

用所得到的五点差分格式进行算例计算近似数值解误差得到了大大提高，常微分方程稳定的情况下差分格式的具有最高阶精度达到五阶。误差达到了10⁻¹⁰，边界处理精度达到六阶时，差分格式精度为七阶，误差低到10⁻¹⁴。当边界差分方程精度达到八阶时，我们得到的差分格式最高精度的阶数为八阶。这个误差精度是我查阅到的差分格式中最小的了。而且这个计算量小，所以我们得到的五点差分格式是可行的并且是实用的。

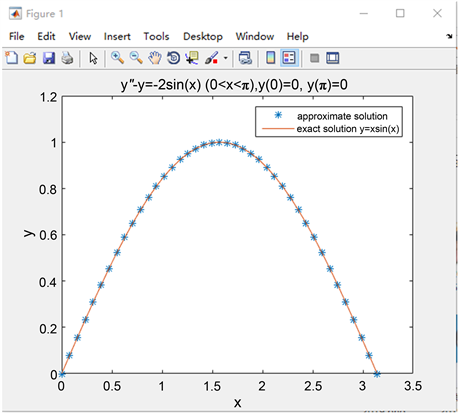
Figure 3. Example 3 Approximate solution and exact solution comparison diagram

图3. 例题3近似解与精确解对比图

本文只对一种简单式的二阶常微分方程 $y^{″} (x) + p (x) y = q (x)$ 边值问题进行求解。由(2.1)得出的五点差分格式最高阶精度为九阶。在数值算例中我们能得到更精确的数值解。同时我们全文考虑的都是在等步长情况下，考虑差分格式的收敛性还可以通过数据来确认，以 $r = e r r / h^{4}$ (err是最大误差，h为步长)，如果存在一个k，使得r常数的上下波动，则这个差分格式收敛，且最终得到k的值就是差分格式的最高阶精度。

本文通过构造具有最高代数精度的二阶导数的组合式近似，构造了具有最高阶精度的等步长的五点差分格式，这是一种构造高阶精度差分格式的方法，可以推广到更多点和变步长情形。构造出格式后，还可以运用广义Peano定理给出它的简洁的误差表达式。

参考文献

[1]	余爱晖, 金怡. 关于一类二阶边值问题的有限差分方法[J]. 杭州师范大学学报(自然科学版), 2007, 6(5): 351-354.
[2]	邹序焱. 用差分方法求解一类二阶两点边值问题[J]. 湖南工业大学学报, 2012, 26(3): 13-15.
[3]	郭晓晔, 蹇玲玲. 求解常微分方程边值问题的差分方法[J]. 长春大学学报, 2015, 25(8): 65-67.
[4]	刘明会. 两点边值问题的一种高精度差分方法[J]. 上海理工大学学报, 2005, 27(1): 68-70.
[5]	周保民. 常微分方程边值问题的高精度差分法[J]. 计算机工程与设计, 1985(4): 31-40.
[6]	李青, 王能超. 解循环三对角线性方程组的追赶法[J]. 小型微型计算机系统, 2002, 23(11): 1393-1395.

为你推荐

友情链接