1. 引言
电机直驱化是指低速大扭矩电机直接拖动负载,由于传动链条中没有减速器,直驱传动系统在效率、可靠性和维护成本方面具有较大优势,电机直驱化已成为机电传动系统的重要发展趋势。在低速大转矩的使用工况下,开关磁阻电机(Switched Reluctance Motor, SRM)是应用较广的一类直驱电机,开关磁阻电机具有一种独特的双凸极结构,定子和转子均由硅钢片叠压而成,因此其结构简单、制造成本低。并且各相之间相互独立可控参数多,开关磁阻电机的调速范围较宽且可容错运行 [1]。直驱电机的转矩输出远大于常规电机,导致直驱电机运行过程的电流和损耗也大于常规电机,长时间运行时电机温升较明显,电机关键结构尺寸受温升影响可能发生变化,如电机定子和转子的热形变,进一步导致电机磁场分布变化,显著影响电机性能。
开关磁阻电机的磁–热耦合响应包括两个方面。首先是磁能转换为热能,电机运行时铜损、铁损等电磁损耗会转变成热能,并作为热源作用于电机本体各部分,导致电机温度场变化;其次是温度场影响磁场,电机温度升高使结构件产生热形变,影响电机的关键尺寸参数,使电机的电磁特性发生变化,进而影响电机性能。国内外对SRM温升及热形变的研究已取得大量的成果,文献 [2] 利用ANSYS有限元仿真软件对125 kW SRM进行了热分析和仿真,得到了在额定工况下电机定子和转子的温度分布。文献 [3] 对SRM各部件典型位置的磁通密度进行分析,利用铁损模型计算SRM热源分布状况,对SRM高真空工况下的温度场进行分析,为电机优化设计提供了理论参考。文献 [4] 对一台电动汽车用110 kW SRM工作时的温度场进行数值分析,为其在实际应用中提供了理论依据。
还有一些研究者对开关磁阻电机温度场仿真技术进行了优化。文献 [5] [6] 提出了一种新型变密度网格划分方法和绕组气隙建模方法,在此基础上进行了相应的有限元分析,结果表明该建模方法有效提高了SRM温度场分析的准确性。文献 [7] 对电机热形变进行了研究,其将电机温度场仿真结果作为激励加载到结构场中,分析了电机的热形变,并进行了实验验证。
本文对开关磁阻电机温度场和热结构场进行了建模,使用Ansys Workbench对电机进行磁–热耦合分析,得到电机连续运转下的温度场分布和因温度引起的尺寸参数变化,并分析了参数变化对电机性能的影响,为开关磁阻电机的电磁设计和散热设计提供了理论基础。
2. 开关磁阻电机磁-热耦合分析模型
本文以24/16外转子直驱开关磁阻电机为例进行磁–热耦合特性分析。对SRM进行温度场和结构场分析时,因转子位置不会影响温度的变化 [8],且电机硅钢片之间填充着导热很差的绝缘物质,可以近似认为电机在轴向无热传递,为减小计算量,可只对单层硅钢片进行建模。图1(a)为在仿真软件中建立的模型,图1(b)为材料赋予和网格划分后的有限元模型,表1为电机的详细参数。

Figure 1. Model and meshing of switched reluctance motor. (a) Model of SRM; (b) Finite element model
图1. 开关磁阻电机模型及网格划分。(a) SRM模型;(b) 有限元模型
由于温度变化对电机参数存在影响且SRM内部热量传递比较复杂,为了方便计算,对建立的电机模型进行简化:1) 各部件材料的导热系数和散热恒定,不随温度发生变化;2) 电机初始温度等于环境温度;3) 电机材料电磁特性不随温度发生变化。
3. SRM磁–热耦合仿真理论基础及损耗分析
3.1. SRM仿真理论基础
SRM的热分析是一个磁–热耦合的过程,将电磁场计算出的损耗作为温度场的热源,在温度场模块中添加散热条件后进行热力学分析,再将温度场分布作为结构场的激励进行热形变的分析,仿真示意如图2所示 [9]。
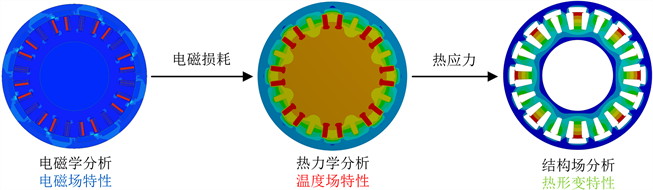
Figure 2. Schematic diagram of magnetic-thermal coupling simulation
图2. 磁–热耦合仿真示意图
3.2. 散热系数的确定
如图3所示,对于风冷的外转子开关磁阻电机,一般存在两个散热边界,一种存在与电机外壳与空气之间,另一种在定子齿和转子齿与气隙空气之间。将机壳与外界空气直接间的自然对流等效到转子的边界上,热对流的计算公式为 [10]:

Figure 3. Two heat dissipation boundaries for external rotor switched reluctance motor
图3. 外转子开关磁阻电机两个散热边界
(1)
式中,k为气体吹拂系数;
为空气流速;T为环境温度。
定转子齿与气隙空气间的对流系数可由式(2)计算得到,即:
(2)
式中,
为努塞尔常数;
为空气热导率;
为气隙长度;
为空气普朗特常数;
为雷诺常数;
为定子外径;
为转子速度;
为空气黏滞度。经计算,各主要参数的数值见表2。
3.3. 开关磁阻电机损耗的求取
理想状态下,开关磁阻电机损耗由铜损和铁损组成,铜损跟相电流有效值的平方成正比;铁损主要来源于硅钢片的磁滞和涡流损耗,因为加工工艺、谐波等因素的存在,准确计算出铁损较困难 [11]。本文使用有限元软件求解SRM各损耗,在Maxwell中添加电压激励以及机械负载,得到如图4所示的在额定工况下SRM的总损耗分布,各项损耗数值见表3。在磁–热耦合分析时,这些损耗数值将直接作为电机各部件的热源 [12]。

Table 3. Losses in various parts of the motor
表3. 电机各部分损耗
3.4. SRM温度场仿真结果
在Workbench中分别设定两个散热系数,经计算得到开关磁阻电机定、转子温度分布。图5为电机连续运行7200 s时定、转子的热场分布云图。
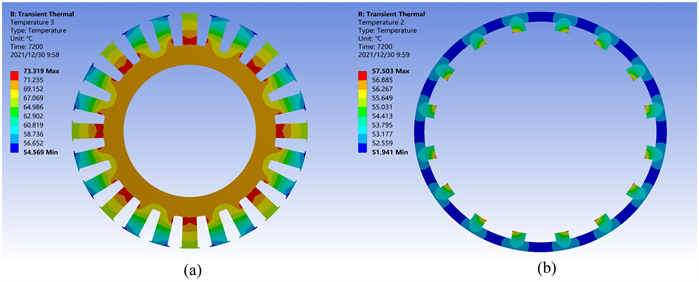
Figure 5. SRM thermal field distribution cloud at 7200 s. (a) Stator; (b) Rotor
图5. 7200 s时SRM热场分布云图。(a) 定子;(b) 转子
由图6可知,当连续运行6000 s左右SRM各部件温度达到稳态值,散热量与生热量实现了基本平衡,温度将不再变化。电机启动后,绕组的温度始终最高,因为启动时绕组上通过了较大的电流产生了大量的铜损,且低速状态下定转子的铁损很小。在热稳态时,最高温度出现在绕组上达到73℃,定子受到绕组的传热较多,温度较转子高。而转子的热量主要来源于定子通过气隙的热流导热和自身的铁损发热,且转子与外界空气直接接触,温度最低。图5中某一相定子凸极温度较其他定子凸极有更高的温度,这是因为电机启动时该相导通,绕组流经较大的电流,在该相产生较大的铜损。

Figure 6. Transient temperature of the SRM components
图6. SRM各部件瞬态温度
4. 开关磁阻电机定、转子热形变分析
电机各部件在温度的影响下会有热胀冷缩现象,各部件会产生形变。关键尺寸的变化会对电磁学和热力学的分析造成影响,尤其定子和转子径向的形变会使得气隙减小,从而会影响电机的性能特性。
4.1. 热形变仿真结果
将开关磁阻电机温度场的分析结果作为激励输入到结构场进行形变分析,并对电机转子外边缘和定子内边缘施加固定约束,经分析得到SRM在热载荷作用下产生的热变形。图7为电机运行7200 s时的热形变云图,可以看出,在热应力的作用下,定、转子都发生了一定量的热形变。
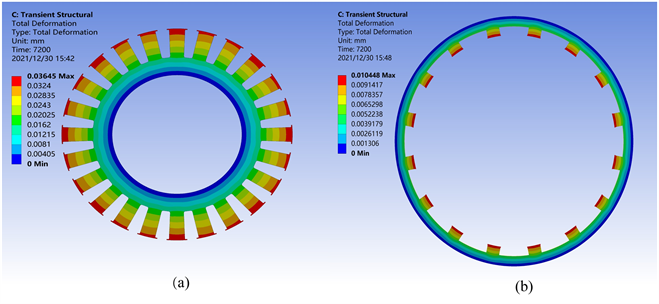
Figure 7. SRM thermal deformation cloud at 7200 s. (a) Stator; (b) Rotor
图7. 7200 s时SRM热形变云图。(a) 定子;(b) 转子
图8显示了定子和转子的瞬态形变量,因定子温度较转子温度高,定子的形变量也比转子的形变量大,并且最大形变量在温度最高的定子极上,为0.03645 mm。因转子各极上温度分布较为均匀,各个转子极的形变量大致相同,最大形变为0.010448 mm。热应力造成的定子、转子总形变量为0.03645 mm + 0.010448 mm = 0.046898 mm,而转子与定子之间的气隙只有0.3 mm,热形变量达到了气隙的15.6%。因此,当开关磁阻电机持续运行一段时间后,发热会对电机性能会造成很大的影响。
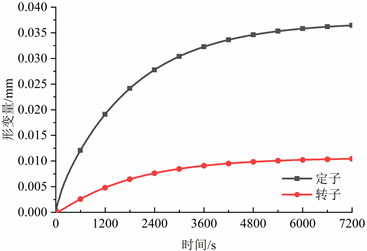
Figure 8. Transient thermal deformation of stator and rotor
图8. 定、转子瞬态热形变
4.2. 热形变对电机性能的影响
分别取电机运行3600 s和7200 s时的定转子热形变量,在Maxwell中建立新的电机模型。从电磁场、电感和扭矩方面对热变形后的电机进行性能评估 [13] [14]。
图9给出了稳态运行0 s、3600 s和7200 s时SRM在10 A电流激励下的磁通密度。通过对比发现,发生热形变后的最大磁通密度会变小。
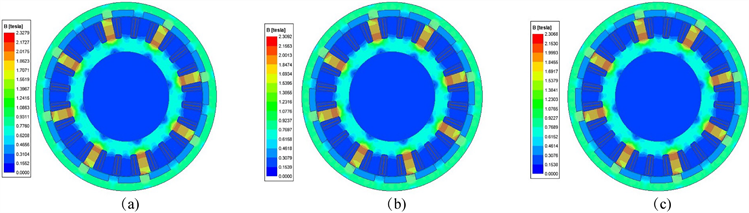
Figure 9. Flux density of SRM at 10 A current. (a) 0 s; (b) 3600 s; (c) 7200 s
图9. 10 A电流下SRM磁通密度。(a) 0 s;(b)3600 s;(c) 7200 s
图10给出了电机稳态运行0 s、3600 s和7200 s发生热形变后在1 A和10 A激励电流下电感随电机角度变化曲线。在1 A激励电流下,电机不对齐位置附近,由于铁心部分未饱和,三个时间节点下电机的电感几乎相等,但是随着铁心部分叠压区域的增加,有较大热形变电机的电感开始逐渐大于热形变量较小电机的电感。在10 A激励电流下,电机的电感值已经饱和,热形变对电感值影响不大。
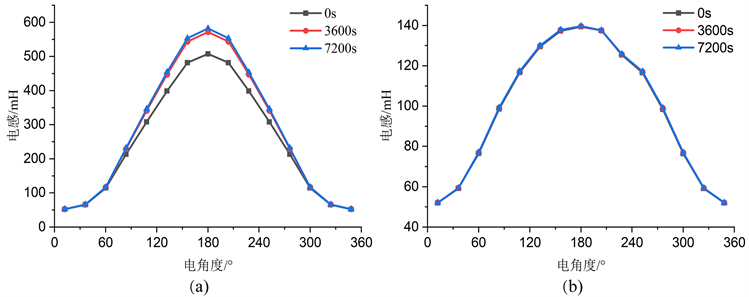
Figure 10. Variation curves of SRM inductance for three deformations under excitation currents. (a) 1 A; (b) 10 A
图10. 励磁电流下三种形变SRM电感变化曲线。(a) 1 A;(b) 10 A
图11给出了电机稳态运行0 s、3600 s和7200 s发生热形变后在1 A和10 A激励电流下扭矩随电机角度变化的曲线。对比可知,热形变对电机扭矩会产生一定的影响,在相同激励电流下,热形变越大电机的扭矩越大,且激励电流越大,热形变对电机扭矩的影响越明显。在1 A电流激励下,7200 s时SRM最大扭矩为1.9 Nm,0 s时的SRM最大扭矩为1.6 Nm,扭矩增大了0.3 Nm;在10A电流激励下,两个时刻下电机最大扭矩增大了2.5 Nm。
5. 总结
为了研究开关磁阻电机在稳态运行下,电机各部件的温度场分布以及因温升引起的热形变,本文使用有限元软件对开关磁阻电机进行了磁–热耦合仿真,分析了热形变对电机性能的影响。结论如下:
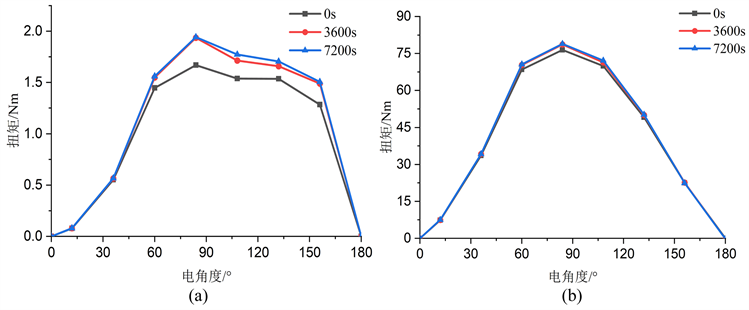
Figure 11. Variation curves of SRM torque for three deformations under excitation currents. (a) 1 A; (b) 10 A
图11. 励磁电流下三种形变SRM扭矩变化曲线。(a) 1 A;(b) 10 A
1) 稳态运行时,电机在各损耗的影响下,电机的温度会缓慢上升,并在6000 s左右温度达到稳态值,并且绕组的稳态温度最高,而转子的稳态温度最低。
2) 在热应力的作用下,定、转子都发生了一定量的热形变。定子的形变量大于转子的形变量,达到热稳态时定、转子的形变量已达到气隙的15.6%。
3) 在热形变的影响下,电机的尺寸参数发生了变化,对电机的性能会产生一定的影响。热形变越大,SRM的最大磁通密度会减小;在电感未达到饱和时,定、转子对中位置下的电感会随着热形变的增大而减小;在相同激励电流下,热形变越大,电机的扭矩会越大,且热形变对扭矩的影响随着激励电流的增加会越明显。
基金项目
国家自然科学基金重点项目(No. 51935007);国家自然科学基金面上项目(No. 51975356)。
NOTES
*通讯作者。