面向模型切割的网格闭合光滑曲线设计

Model-Cutting Oriented Closed Curve Design on Surface Mesh

摘要: 在网格上鲁棒地设计光滑曲线在计算机辅助设计领域中有广泛的应用。针对网格表面模型切割问题，本文提出一种网格表面离散闭合光滑曲线的设计方法。该方法将离散采样点限制在网格的边或者顶点上，以减少切割算法的计算量。输入一组位于网格上的插值点，本文首先生成一条经过所有插值点的初始曲线，随后本文利用高斯赛德尔迭代优化一个离散曲线曲率能量来保证曲线的光滑性。实验结果表明本文算法可以满足实时交互需求，且具有很高的鲁棒性。

Abstract: Robust curve design on surface meshes with flexible controls is useful across applications but remains challenging. Aiming at hole cutting on the mesh surface, this paper proposes an approach for designing discrete closed smooth curves on the mesh surface. We restrict the discrete sampling points to the edges or vertices of the mesh to reduce the computational complexity of the cutting algorithm. Inputting a set of interpolation points on the mesh, we first generate an initial curve that passes through all the interpolation points, and then we use Gauss-Seidel iterative optimization to optimize the curvature energy of a discrete curve to ensure the smoothness of the curve. The experimental results show that the proposed algorithm can meet the real-time interaction requirements and has high robustness.

1. 引言

曲线设计是计算机图形学与计算机辅助设计领域中的一个基本问题。曲线设计虽然在欧几里得空间(后文简写为欧氏空间)中的研究已经十分完备，但是在曲面空间中(如三角形网格)设计曲线仍然面临着许多困难。然而，在曲面上设计曲线有着许多的应用场景，如网格孔洞切割、特征识别、艺术设计、制造业、虚拟现实、曲面计算几何等。除了光滑性、插值性、特征感知等一些公共的性质与欧氏空间中的相同之外，曲面曲线设计特别需要将曲线限制在曲面空间中，使得曲面曲线设计更加具有挑战性。这种约束通常被称为流形约束。

为了设计满足流形约束的曲面曲线，大多数方法把曲线表示为离散多边形折线，这类方法为首先将连续的曲线表示为离散的多边形折线，随后通过优化步骤来使结果曲线满足插值性、光滑性、流形约束的需求。其中，如何处理流形约束是这类问题中最关键的问题，目前关于这个问题的解决方法可以分为多个种类：基于投影的方法 [1] [2]、基于光滑的方法 [3] 与基于参数化的方法 [4]。对于离散曲线而言，这些方法的耗时程度主要由曲线的采样密度决定，这是计算曲线形状的先决条件。

针对于在网格上设计闭合曲线并需要进行孔洞切割时，过高的曲线采样率可能使得孔洞切割算法变得十分复杂，导致算法效率低下，因此考虑到算法的实时交互性，本文使用离散多边形折线来表示曲线。

本文采用离散多边形折线来表示曲线，将曲线上的采样点限制在网格的边上，并使用三种拓扑操作来保证曲线满足流形约束。为了进一步减少优化变量，本文使用采样点所在边的两个端点的线性插值来表示采样点位置。随后通过基于高斯赛德尔迭代的优化框架对初始曲线进行优化。值得一提的是，该优化框架可以用于多种应用，如曲面网格的测地线设计。

2. 相关工作

过去十几年来，在连续流形和离散流形上进行曲线设计已经进行了充分的研究，有许多与该问题相关的文献。本文主要关注的是在离散网格曲线上进行曲线设计的问题。根据曲线表示方式的不同，现有的曲面曲线设计方法可以被分为隐式与显式方法，本文主要介绍显式方法，这类方法直接在网格上设计一条显式曲线，以满足若干个关键约束，如平滑度，插值约束与流形约束。隐式方法也被称为水平集法 [5] [6] [7]，这类方法需要求解网格上具有特定边界条件光滑标量场的偏微分方程，然后根据水平集来抽取出结果曲线。这类方法十分鲁棒且严格满足流形约束，但是由于偏微分方程需要对整个网格进行求解，所以该类方法十分耗时，因此本文没有采用该类方法来设计曲线。

与在欧氏空间中设计曲线不同，在网格曲面上设计曲线的关键为将曲线限制在曲线上，在优化过程中，本文也称其为流形约束。目前，大多数的方法都首先将连续曲线离散化为折线，然后通过一个优化步骤使得曲线达到一个最理想的状态。一些方法 [8] [9] 使用局部单片参数化来解决复杂的流形约束，在参数域中，可以应用欧氏空间中的曲线设计方法，然后将结果曲线映射回曲面。然而，如何找到合适且正确的参数化区域是一个较难解决的问题，并且参数化过程中造成的畸变也是无法避免的问题。另一类方法在松弛平滑度约束的同时保持流形约束，在优化过程中，该类方法在一个特定能量的驱动下逐渐将一条初始曲线光滑化。Jung等 [10] 将图像领域中著名的活动轮廓模型扩展到网格曲面上，通过蛇形能量扩散位于网格边上的闭合折线来获得结果曲线。Ji等 [11] 通过允许曲线通过网格面，即在迭代过程中自适应地合并或者拆分折线上的顶点改进了结果。Lawonn等 [3] 进一步优化该算法，他们通过求解一个带权重的拉普拉斯能量以最小化测地曲率。由于使用了严格的流形约束，这类方法具方法有很高的鲁棒性，但通常无法保证算法的效率，且容易陷入局部最小值。另一类方法松弛了流形约束，并在网格一定范围内的外围空间求解一条光滑的曲线然后将该曲线投影回网格曲面。Hofer等 [1] 在离散后的折线定义样条曲线能量，使用投影梯度法对曲面附近的能量均进行优化。之后，他们又提出了样条曲线能量的高阶版本 [12]，并使用相同的策略在曲面网格上进行数据拟合。Hofer等 [13] 总结了该类方法并展示了他们利用该算法进行的应用。然而，投影步骤依赖于MLS (Moving Least Square)的局部拟合，这通常来说非常耗时，并且可能会有鲁棒性问题。刘斌等 [14] 提出了一种测地B样条插值方法，他们运用最近点投影法将B样条插值曲线映射到网格曲面上，然后采用插值误差反向补偿法使曲线逐渐逼近曲面。但该方法同样耗时且投影算法可能存在多解，从而无法处理复杂曲面。最近几年，Jin等 [2] 使用壳空间来获得鲁棒的距离求解与投影算子，该方法同时吸取了基于光滑与基于投影算法的优点，而他们算法的瓶颈在于如何构造一个合适厚度的壳空间。总结来说，在网格上优化折线为当前主流且较为容易的方法，但是另一方面，这类方法预先确定了采样密度。此外，不正确的采样点数量估计可能会影响曲线的平滑度或者计算效率。

3. 方法

3.1. 问题与算法概述

令 $\mathcal{S}=\langle V_{\mathcal{S}},F_{\mathcal{S}}\rangle$ 表示一个嵌在欧氏空间 ${ℝ}^3$ 中的无自交、可定向的流形三角网格。其中 $V_{\mathcal{S}}$ 与 $F_{\mathcal{S}}$ 分别表示网格的顶点与面片集合。本方法的目标是在曲面 $\mathcal{S}$ 上设计一条“视觉上光滑的”曲线 $\mathcal{C}$ ，该曲线插值一组有序的点 $X={\left\{x_i\in \mathcal{S}\right\}}_{i=1}^N$。该算法框架将曲线优化问题转化为如下优化问题：

$\begin{array}{l}\underset{\mathcal{C}}{\min }{E}_{\mathrm{int}}\left(\mathcal{C}\right)+\mu E_{\text{ext}}\left(\mathcal{C}\right)\\ \text{s}\text{.t}\text{.}{x}_i\in \mathcal{C},i=1,2,\cdots ,N\\ C\in S\end{array}$ (1)

其中 $E_{\mathrm{int}}\left(\mathcal{C}\right)$ 表示内部能量。该能量根据应用场景的不同而改变，如在光滑曲线设计中，该能量就表示光滑能量，而在测地线设计中，该能量就为曲线长度能量。该能量的表示为：

$E_{\mathrm{int}}\left(\mathcal{C}\right)={\displaystyle {\int }_{\mathcal{C}}{E}_{\mathrm{int}}\text{d}s}$ (2)

第一个约束为插值约束，曲线必须经过给定的插值点序列 $X={\left\{x_i\in \mathcal{S}\right\}}_{i=1}^N$ ；第二个约束为流形约束，指曲线必须位于曲面上。

本文算法采用离散多边形折线来表示曲面曲线，其中离散曲线上每一个采样点为一个网格点 $s$ ，网格点有位于网格顶点上的点、位于网格边上的点与位于网格面片上的点三种，则离散曲线 $\mathcal{C}$ 可以表示为离散网格点的有序序列 $\mathcal{C}=\left\{s_1,\cdots ,s_N\right\}$ ，本文规定离散曲线 $\mathcal{C}$ 上的网格点除了插值点之外，均不能为面片点。这种离散曲面定义方法的好处主要有三点：

1) 这种曲线表示方式能够保证曲线严格位于曲面上，消除了难以求解流形约束；

2) 这种曲线表示方式相对于样条曲线有更高的自由度，优化过程中直接优化采样点位置；

3) 这种曲线表示方式对于某些应用十分友好，如孔洞切割与测地线曲线设计。

离散化以后的优化目标可以表示为：

$E_{\mathrm{int}}\left(\mathcal{C}\right)={\displaystyle \underset{i=1}{\overset{N}{\sum }}{E}_{\mathrm{int}}\left(s_i\right)}$ (3)

然而在网格曲面上直接优化该能量较为困难，因为需要处理网格点的拓扑约束，即网格点只能位于网格顶点与边上，所以本节算法使用网格点 $s_i$ 所在边 $e_i$ 的端点通过线性插值来表示：

$P_i=A_i+t_i\left(B_i-A_i\right)$ (4)

其中 $P_i$ 为网格点 $s_i$ 的位置坐标， $A_i,B_i$ 为 $e_i$ 的两个端点， $t_i\in \left[0,1\right]$ 为线性插值的参数，因此，本节算法中的离散曲线可以表示为：

$\mathcal{C}=\left\{\left\{e_1,t_1\right\},\cdots ,\left\{e_N,t_N\right\}\right\}$ (5)

这种表示方法的优势在于：

1) 将每个网格点的优化变量由之前的三个变为单变量问题，大大降低了求解的复杂度；

2) 这种表示方式消除了网格点的拓扑约束，简化了计算。

本文算法由一条初始曲线开始，经过优化迭代之后获得最终曲线。通过计算每一个插值点 $x_i,x_{i+1},i=1,\cdots ,N-1$ 之间的迪杰斯特拉路径，并将 $N-1$ 条迪杰斯特拉路径按顺序首尾相接得到初始曲线。注意，若目标曲线为封闭曲线，则需要额外计算 $x_N,x_1$ 之间的迪杰斯特拉路径。

在优化过程中，若某个网格点位于网格顶点上，则若直接移动该点可能使得曲线不严格位于网格曲面上，所以需要根据该点的优化方向将网格点 $s_i$ 分裂，以保证曲线严格位于网格曲面。此外，若 $\overline{s_{i-1}{s}_i}$ 与 $\overline{s_i{s}_{i+1}}$ 位于网格的同一个面片，为了减少计算的复杂度，本节算法将网格点 $s_i$ 删除，即把 $\overline{s_{i-1}{s}_i}$ 与 $\overline{s_i{s}_{i+1}}$ 融合成 $\overline{s_{i-1}{s}_{i+1}}$。本节算法所使用的一系列拓扑操作(分裂、融合与移动)将在第3.2节详细阐述。

在迭代过程中，需要对曲线的拓扑进行更新，因此，全局的优化方法并不适合本节算法。本节算法采用高斯塞德尔迭代法，将优化问题分散到每一个网格点 $s_i$ 上进行顺序迭代求解，每一个网格点 $s_i=\left\{e_i,t_i\right\}$ 的优化问题可以表示为：

$\arg \underset{t_i}{\min }{E}_{\mathrm{int}}\left(e_i,t_i\right)$ (6)

若子问题 $E_{\mathrm{int}}\left(e_i,t_i\right)$ 为凸优化问题，则能够保证高斯塞德尔迭代的收敛性。

3.2. 拓扑操作

在本节算法中，由于曲线顶点被限制在网格边上，所以在优化过程中，上一次迭代中单个网格点的移动可能无法保证曲线严格位于网格曲面上，或者，上一次迭代有冗余基函数需要被删除。因此本节算法需要一系列拓扑操作以改变曲线基函数的数量与位置，本节算法参考了等 [11] 的方法，使用三种基本的拓扑操作来完成，分别为移动，分裂与融合。

当曲线顶点位于网格边上时，在优化过程中该顶点需要在边上移动(图1(a))，本节算法使用公式(4)来表示网格点的位置，这样既能够保证顶点只能在边上移动的约束，又可以将顶点位置优化转化为一个单变量问题，方便求解。

当曲线顶点位于某个网格顶点上，首先根据梯度方向 $\nabla E_{\mathrm{int}}\left(s_i\right)$ 对网格点 $s_i$ 进行移动，由于网格点 $s_i$ 只能在边上移动，所以若只将网格点 $s_i$ 移动到其某一条邻接边上的话，有可能使得曲线 $\mathcal{C}$ 不满足流形约束，如图1(b)，若 $s_i$ 只是移动为 $s_i^0$ ，没有进行分裂操作，那么新的曲线段 $s_{i-1}{s}_i^0{s}_{i+1}$ 不满足流形约束。因此在优化过程中，需要将 $\Vert \nabla E_{\mathrm{int}}\left(s_i\right)\Vert \ne 0$ 的网格点 $s_i$ 正确地分裂到若干条邻接边上，在满足曲线流形约束的同时，使得优化能量下降。为方便表述，本文引入“楔形”的概念，顶点的一环邻域可被曲线顶点的前后两个点组成的线段分割为两个区域(如图2)，而顶点将被分裂到某个楔形上，一旦曲线顶点被分裂到某个楔形上，曲线顶点将被替换为楔形所有入射边上的曲线顶点。在图2中，若网格点 $s_i$ 被分裂到绿色楔形，则 $s_i$ 将被分裂到 $e_0,e_1$ 上，而若被分裂到蓝色楔形上，那么 $s_i$ 将被分裂到 $e_3,e_4,e_5$ 上。

(a) 移动 (b) 分裂(c) 融合

Figure 1. Topological operation

图1. 拓扑操作

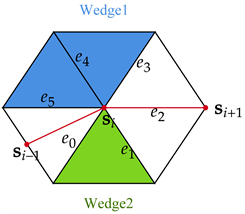
Figure 2. The blue and green regions are wedges divided by red segments

图2. 楔形，绿色与蓝色区域为曲线(由红色网格点连接)分割出的两个楔形

当某个网格点的前后两个线段 $\overline{s_{i-1}{s}_i}$ 与 $\overline{s_i{s}_{i+1}}$ 位于同一个面片，且该顶点非插值点，则该网格点为冗余点，该步骤被称为融合(见图1(c))。对于本节算法所使用的两个应用而言，删去冗余网格点可以降低曲线拓扑结构的复杂度，减小优化问题规模，加速优化收敛。

3.3. 光滑曲线设计

为在网格上设计满足插值约束的光滑曲线，给定一条位于网格曲面 $\mathcal{S}$ 上的离散曲线 $\mathcal{C}$ ，为了使得封闭曲线在连接处同样具有光滑性，不同于Ji等 [11] 使用的内部能量，本文采用一种离散曲线上的拉普拉斯能量来保证曲线的光滑性。此外，由于曲面为嵌入在欧氏空间中的二维流形，曲面表面的曲线可能会收到曲面曲率的影响。如此一来，在欧氏空间中的曲线质量度量需要消除曲面表面的影响，本文采用指数映射来消除这种影响。

具体而言，本文将公式(3)改写为离散曲线曲率能量：

$E_{\mathrm{int}}\left(\mathcal{C}\right)={\displaystyle \underset{i}{\sum }{\theta }_i^2}$ (7)

由于优化过程中本文的优化框架每次只更新一个网格点 $s_i$ ，需要将公式(7)离散化。曲线的曲率与曲线网格点 $s_i$ 的夹角正相关，所以本文将公式(7)离散化为：

$E_{\mathrm{int}}\left(s_i\right)={\theta }_{i-1}^2+{\theta }_i^2+{\theta }_{i+1}^2$ (8)

其中 ${\theta }_i\in \left[0,\pi \right]$ 为网格点 $s_i$ 夹角的补角见图3。

Figure 3. Curvature of discrete curves

图3. 离散曲线曲率

为了消除曲线曲率的影响，本文使用指数映射 [15] 将 $s_{i-2}{s}_{i-1}{s}_i{s}_{i+1}{s}_{i+2}$ 映射到平面中，再在平面中求解公式(8)。

3.4. 测地线设计

通过使用不同的能量 $E_{\mathrm{int}}\left(\mathcal{C}\right)$ ，本文算法能够被用于各种不同类型曲线的设计，本节以设计测地线为例，展现该优化框架的通用性。

在设计测地线时，本文将曲线长度作为优化目标，通过最小化曲线长度来近似逼近测地线。值得一提的是，本文所求得的这种测地线并不是全局中最短的测地线，而是测地线的一种逼近。由于本文的曲线设计均由一条初始曲线开始，然后经过迭代不断优化曲线直到能量收敛，这种优化方式容易使得曲线陷入局部最小值。

具体地，本小节将公式(1)中的 $E_{\mathrm{int}}\left(\mathcal{C}\right)$ 写为曲线 $\mathcal{C}$ 的长度，即曲线积分：

$E_{\mathrm{int}}\left(\mathcal{C}\right)={\displaystyle {\int }_{\mathcal{C}}\text{d}s}.$

其中，公式(3)中的 $E_{\mathrm{int}}\left(s_i\right)$ ，表示为前后两端折线段的长度之和：

$E_{\mathrm{int}}\left(s_i\right)=\Vert s_{i-1}{s}_i\Vert +\Vert s_i{s}_{i+1}\Vert$ (9)

对于开曲线而言，公式(9)可以重写为如下形式：

$E_{\mathrm{int}}\left(\mathcal{C}\right)=\Vert s_1{s}_2\Vert +2{\displaystyle \underset{i=2}{\overset{N-1}{\sum }}\Vert s_i{s}_{i+1}\Vert }+\Vert s_{N-1}{s}_N\Vert$

可以证明， $E_{\mathrm{int}}\left(s_i\right)$ 所组成的优化问题公式(6)，为一个凸优化问题，且能够高效地求得解析解。

对于曲线 $\mathcal{C}$ 中任意两段连续线段 $\overline{s_{i-1}{s}_i}$ 与 $\overline{s_i{s}_{i+1}}$ ，设边 $e_i$ 为网格点 $s_i$ 所在边，将点 $s_{i-1}$ 与 分别投影到边 $e_i$ 上，得到投影点 ${s^{\prime }}_{i-1}$ 与 ${s^{\prime }}_{i+1}$。令 $l_1=\Vert s_{i-1}{s^{\prime }}_{i-1}\Vert ,l_2=\Vert s_{i+1}{s^{\prime }}_{i+1}\Vert$。如图4，将与边 $e_i$ 相邻的两面片摊平，若要使得 $E_{\mathrm{int}}\left(s_i\right)$ 则可以在平面中直接连接 $s_{i-1}$ 与 $s_{i+1}$ ，其与 $e_i$ 的交点记为 $o$。不难看出 $\Delta s_{i-1}{s^{\prime }}_{i-1}o~\Delta s_{i+1}{s^{\prime }}_{i+1}o$ ，因此可以得出 $\Vert s_{i-1}{s^{\prime }}_{i-1}\Vert /\Vert s_{i+1}{s^{\prime }}_{i+1}\Vert =\Vert s_{i-1}o\Vert /\Vert s_{i+1}o\Vert$。即

$o=w_1{s}_{i-1}+w_2{s}_{i+1}$

其中

$w_1=\frac{\Vert s_{i+1}{s^{\prime }}_{i+1}\Vert }{\Vert s_{i-1}{s^{\prime }}_{i-1}\Vert +\Vert s_{i+1}{s^{\prime }}_{i+1}\Vert }$

$w_2=\frac{\Vert s_{i-1}{s^{\prime }}_{i-1}\Vert }{\Vert s_{i-1}{s^{\prime }}_{i-1}\Vert +\Vert s_{i+1}{s^{\prime }}_{i+1}\Vert }$

那么优化问题(6)可以转化为一个简单的二次规划问题：

$\arg \underset{t}{\min }{\Vert P_i\left(t\right)-O\Vert }_2^2$

并且可以根据获取该问题的解析解：

$t=\frac{\Vert o-A_i\Vert }{\Vert B_i-A_i\Vert }$ (10)

其中 $A_i,B_i$ 为 $s_i$ 所在边 $e_i$ 的两个端点。根据上文所述，本小节提出的测地线能量为凸，因此本文的优化框架能够保证其收敛。

Figure 4. Plan view of faces adjacent to mesh points

图4. 网格点相邻面的平面视图

3.5. 孔洞切割

给定一条本文光滑曲线设计算法生成的一条网格曲面的闭合曲线 $\mathcal{C}$ ，该闭合曲线能将原曲面 $\mathcal{S}$ 划分为两个子曲面 ${\mathcal{S}}_1,{\mathcal{S}}_2$。孔洞切割算法的目的就是获取两个子曲面 ${\mathcal{S}}_1,{\mathcal{S}}_2$ ，如图5(a)所示。本文首先对整个网格的面片进行标记，再根据标记搜索完全位于内部区域 ${\mathcal{S}}_1$ ${\mathcal{S}}_2$ 区域的三角形面片。最后对曲线经过的面片进行重网格化并添加到外部或者内部区域中。

标记分为三种类型，分别为外部、内部与中间。外部与内部面片分别表示该面片完全位于曲线 $\mathcal{C}$ 划分两个区域的外部与内部，面片的内部(不包括面片的边界)没有曲线经过。而中间则表示有曲线通过的面片，如图5(b)所示。

(a) 曲线划分两个区域 (b) 标记面片类型 (c) 构建内外区域 (d) 处理中间面片

Figure 5. Hole-cutting pipeline

图5. 孔洞切割流程

本文采用区域增长算法来搜索内部与外部的区域。具体而言，根据标记的结果，选取一个内部或者外部的三角形面片为种子，再根据广度优先搜索对区域进行增长，增长的终止条件为搜索到标记中间的面片，区域增长的结果见图5(c)。

最后，本文对中间有曲线经过的面片进行重新划分(图5(d))，由于本文将曲线顶点限制在网格边上，所以对于三角形划分的情况可以简单归结为3种类型，即两个曲线顶点都位于网格顶点上，两个曲线顶点都位于网格边上，与一个曲线顶点位于网格顶点上另一个网格顶点位于网格边上见图6。

(a) 网格顶点-网格顶点 (b) 网格顶点-网格边 (c) 网格边-网格边

Figure 6. Hole-cutting pipeline

图6. 孔洞切割流程

4. 实验结果与分析

本算法的实验环境为4.1 GHz IntelCorei5 CPU，32 GB内存。本文实现该算法为一个单线程C++程序。线性代数部分的计算由Eigen [16] 库实现，数值求解使用CppNumerical Solvers [17] 实现。本文在若干个网格上实验了该算法，并与同类型的相关方法作了比较。

4.1. 收敛性

显然，本文所使用的曲线光滑能量(公式(8))与测地线能量(公式(9))均为凸，因此高斯赛德尔迭代的收敛条件表明该算法在有限次迭代之后一定可以收敛 [18]。本文对多组数据进行收敛性实验并绘制了能量收敛图，结果如图7。

Figure 7. Convergence of the Menou model

图7. 猫咪模型收敛图

4.2. 曲线设计与切割效果

用户给定一组位于网格上的插值点，本文能够生成一条位于网格上的光滑离散曲线，并且对于封闭曲线而言能够进行切割应用。

图8分别在鸟与牛模型上设计开曲线，结果表明本文算法可以保证曲线的光滑性。

(a) 幽灵模型上的开曲线 (b) 牛模型上的开曲线

Figure 8. Results of open curves

图8. 开曲线结果

本文的曲线设计算法能够用于模型的孔洞或者部件切割。图9与图10在给出了曲线切割的一些实例，本文在这些模型上设计封闭曲线并进行切割，图9为对曲线所围孔洞进行切割，而图10为对曲线所围部件进行切割

(a) 维纳斯模型上的闭曲线 (b) 维纳斯模型切割结果 (c) 猫咪模型上的闭曲线 (d) 猫咪模型切割结果

Figure 9. Results of closed curves hole cutting

图9. 闭曲线孔洞切割结果

(a) 半兽人模型上的闭曲线 (b) 半兽人模型切割结果 (c) 大象模型上的闭曲线 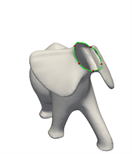(d) 大象模型切割结果

Figure 10. Results of closed curves part cutting

图10. 闭曲线部件切割结果

4.3. 测地线设计

本文能够生成位于网格模型上任意两点之间的近似测地线，本文在女巫模型上测试了一个起始点到。模型上所有网格顶点的测地线，并选择部分展示于图11。

Figure 11. Geodesic curves of the witch model

图11. 女巫模型的测地线结果

4.4. 效率

本算法最为耗时的部分为迭代过程中所涉及的线性方程求解。由于本文将局部的优化问题的变量优化到一个，因此求解效率较高，可以满足用户实时交互的需求。表1列出了在各个模型上设计封闭曲线与切割孔洞的时间。由表1可见：算法与网格模型的规模相关度较小，主要取决于曲线所经过网格的面积。

Table 1. Cost time of generating closed curve and hole-cutting on various models

表1. 各个模型上封闭曲线的生成时间与切割耗时

5. 结论

本文主要针对三角形网格的孔洞切割问题提出了一种网格表面闭合光滑曲线的设计方法，该方法能够在网格表面设计视觉光滑的闭合离散曲线。该算法利用离散曲线采样点的夹角来表示曲线的曲率，并根据曲率来设计光滑能量。在优化过程中利用采样点所在的网格边两端点表示采样点位置，能够减少优化变量并解决流形约束问题。此外本文所设计的离散封闭曲线能够很容易地进行孔洞切割应用。本文所提出的优化框架能够容易地扩展到测地线的设计。实验结果表明本文提出的方法可以满足实时响应交互需求并且足够鲁棒，在今后的研究中有一定的参考价值。