2021年高考数学I卷评析——基于核心素养测评框架

Research on Mathematics Volume I of the 2021 National College Entrance Examination—Based on Core Literacy Evaluation Framework

摘要: 本文基于“主题内容 × 素养成分 × 观测指标”的核心素养测评框架探究2021年高考数学I卷对数学核心素养的考查是否满足《普通高中数学课程标准(2017年版)》的要求。研究发现：该卷对各核心素养均有考查但分布不均，其中数学方法素养考查最多，数学思维素养次之，数学工具素养考查最少；在数学知识、问题解决和数学思维三个维度的考查中，数学思维维度的考查仍有待提高；在三个水平的考查上，对于水平三的考查不满足课标要求。故本文建议：优化核心素养考查分配，加重数学工具素养考核；增强数学思维维度测查，提高水平三层次的考查。

Abstract: Based on core literacy evaluation framework about “theme content × literacy component × observation index”, this paper aims to explore whether the examination of mathematics core literacy in volume I of the 2021 National College Entrance Examination meets the requirements of Mathematics Curriculum Standards for Senior High Schools (2017). The study found that volume I examined all core literacies but was uneven. Among them, mathematical method literacy was the most, mathematical thinking literacy was the second, and mathematical tool literacy was the least; in the examination of the three dimensions of mathematical knowledge, problem solving and mathematical thinking, the examination of the dimension of mathematical thinking needs to be improved; in the examination of three levels, the examination of level three does not meet the requirement of the curriculum standard. Therefore, I suggest: optimizing the examination of core literacy and increasing the examination of mathematical tool literacy; strengthening the examination of mathematical thinking dimension and improving the examination of level three.

1. 引言

2014年3月，《教育部关于全面深化课程改革 落实立德树人根本任务的意见》提出将研制各学段学生发展核心素养体系，明确学生应具备的适应终身发展和社会发展的品格和关键能力，明确学生完成不同学段、不同年级、不同学科学习内容后应该达到的程度要求 [1]。2018年1月，教育部印发了《普通高中数学课程标准(2017年版)》，当中凝练了六大数学核心素养：数学抽象、逻辑推理、数学建模、数学运算、直观想象和数据分析，并基于数学核心素养提出了学业质量水平，给出了关于高考命题的建议，其中提到命题时应注重对学生进行数学核心素养的考查，处理好数学核心素养与知识技能的关系 [2]。2019年12月，教育部颁发了《中国高考评价体系》，该体系由“一核四层四翼”构成，主要回答了“为什么考”“考什么”和“怎么考”的问题，其中“考什么”明确了学科素养是高考着重考查的内容之一 [3]。可见，高考不仅是考查学生知识水平的重要途径，也是检测学生的数学核心素养发展情况的关键手段，由此基于数学核心素养展开关于高考数学试题的评价研究显得尤为重要。

2. 核心素养测评框架简介

《普通高中数学课程标准(2017年版)》(以下简称《课标》)将六大数学核心素养分别进行了三级水平划分，但各水平的测评维度和观测指标不够清晰，可操作性不够强，鉴于此，许多学者展开了关于数学核心素养测评框架的构建研究。比如，喻平借鉴了布卢姆、PISA和SOLO模型中的优点，从知识学习的角度切入将数学核心素养划分为知识理解、知识迁移和知识创新三种水平 [4]；李华等人根据喻平提出的数学核心素养划分标准，构建了包含评价指标体系、指标权重和评价标准在内的数学核心素养教育评价表 [5]；俞梦飞等人对数学核心素养进行了具体表现划分和水平划分，构建了数学核心素养考查的评价框架 [6]；谢晖、彭乃霞则在李华和俞梦飞等人的研究基础之上进一步做出了改进，对每一个数学核心素养的具体表现进行了编码，并且确定了每一个水平层次的权重 [7]。

朱立明采用文献法、问卷调查法、访谈法和统计分析方法确定了数学核心素养的测评维度和观测指标，从而构建了“主题内容 × 素养成分 × 观测指标”的三维测评框架 [8]，如表1所示，表2是对测评框架中的9个观测指标的具体描述，该描述在原作者描述的基础上进行了适当的扩充。

Table 1. Three dimensional evaluation framework of mathematics core literacy

表1. 数学核心素养的三维测评框架

Table 2. Measurement dimensions and observation indexes of mathematics core literacy

表2. 数学核心素养的测评维度与观测指标

此外，朱立明为了探索高考中数学核心素养的测查与《课标》要求的一致性，构建了“层面架构 ×认知水平 × 主题内容”的一致性分析框架，并基于此分析框架对高中数学必修课程与选择性必修课程的主题内容进行编码，将每条主题内容划归到相应的核心素养、层面架构和认知水平当中，从而得到《课标》关于“层面架构 × 认知水平 × 主题内容”的编码结果 [9]，具体如表3所示。

Table 3. Examination requirements of Curriculum Standards for mathematics core literacy

表3. 《课标》对数学核心素养的考查要求

3. 2021年高考数学I卷评析

2021年高考数学I卷是在新课标发布、新教材推广和高考评价体系实施的背景之下命制出来的，对数学课堂教学改革具有积极的导向作用，同时也对未来的文理不分科高考命题具有重要的参考作用，故本文选取2021年高考数学I卷(以下简称2021全国I卷)作为研究对象，基于表1的三维测评框架探究其在数学核心素养考查方面是否满足《课标》的要求。

3.1. 编码示例及结果

3.1.1. 编码示例

一道试题可能涉及到对多种数学核心素养的考查，因此在进行编码的过程中，本文将根据择重性原则，使得每道试题至多对应三种素养，每种素养只能对应一个维度和一个水平层次。由于每道选择题和填空题的分值均为5分，而每道解答题的分值均在10分以上，差异较大，故在对解答题进行编码时，按照小题进行拆分。编码过程中分别使用字母A，R，M，I，O，D来代表数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析，下面将从选择题、填空题和解答题当中各选取一题来进行编码示例。

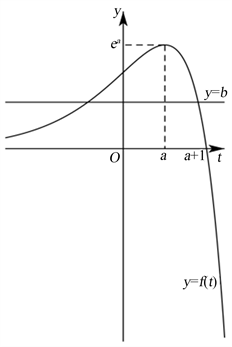
例1 【选择题第7题】过点 $\left(a,b\right)$ 可以作曲线 $y={\text{e}}^x$ 的两条切线，则( )

A. ${\text{e}}^b<a$ B. ${\text{e}}^a<b$ C. $0<a<{\text{e}}^b$ D. $0<b<{\text{e}}^a$

分析：首先，假设点 $P\left(t,{\text{e}}^t\right)$ 为切点，则可求得曲线在点P处的切线方程为 $y={\text{e}}^{t}x+\left(1-t\right){\text{e}}^t$。由于切线过点 $\left(a,b\right)$ ，故有 $b=\left(a+1-t\right){\text{e}}^t$。构造函数 $f\left(t\right)=\left(a+1-t\right){\text{e}}^t$ ，则 $f^{\prime }\left(t\right)=\left(a-t\right){\text{e}}^t$ ，分类讨论可知当 $t<a$ 时 $f\left(t\right)$ 单调递增， $t>a$ 时 $f\left(t\right)$ 单调递减，从而可得 $t=a$ 时有 $f{\left(t\right)}_{\max }={\text{e}}^a$。接着画出函数 $f\left(t\right)$ 的图像，将问题转化为直线 $y=b$ 与曲线 $y=f\left(t\right)$ 的交点问题，由图可知，当 $0<b<{\text{e}}^a$ 时直线 $y=b$ 与曲线 $y=f\left(t\right)$ 有两个交点。在运算求解过程中，学生需理解曲线 $y={\text{e}}^x$ 在点P处的导数即为切线方程的斜率，能够构建导数与函数单调性的关系，故编码为O-K-2。在推理论证的过程中，学生需要综合运用分类思想、转化思想、函数与方程思想和数形结合思想来判断得出 $0<b<{\text{e}}^a$ 时，过点 $\left(a,b\right)$ 可以作曲线 $y={\text{e}}^x$ 的两条切线，考察了逻辑推理素养，编码为R-T-3。此外，求解过程中利用图形语言来描述和分析问题，通过直观地观察直线 $y=b$ 与曲线 $y=f\left(t\right)$ 图像的交点个数来获得答案，考查了直观想象素养，编码为I-S-2。

例2 【填空题第16题】某校学生在研究民间剪纸艺术时，发现剪纸时经常会沿纸的某条对称轴把纸对折，规格为20 dm × 12 dm的长方形纸，对折1次共可以得到10 dm × 12 dm，20 dm × 6 dm两种规格的图形，它们的面积之和 $S_1=240{\text{dm}}^2$ ，对折2次共可以得到5 dm × 12 dm，10 dm × 6 dm，20 dm × 3 dm三种规格的图形，它们的面积之和 $S_2=180{\text{dm}}^2$ ，以此类推，则对折4次共可以得到不同规格图形的种数为 ；如果对折n次，那么 ${\displaystyle {\sum }_{k=1}^n{S}_k}=$ dm²。

分析：本题以民间剪纸艺术为背景，主要考查了数列求和问题。由于对折1次产生两种不同规格的图形，而对折2次产生3种不同规格的图形，故可推测剪纸对折n次后将会产生 $n+1$ 种不同规格的图形。通过观察每次对折后纸张的长和宽的变化，得到对折3次后的图形规格为： $\frac{5}{2}\times 12,5\times 6,10\times 3,20\times \frac{3}{2}$ ，对折4次后的图形规格为： $\frac{5}{4}\times 12,\frac{5}{2}\times 6,5\times 3,10\times \frac{3}{2},20\times \frac{3}{4}$ ，可以发现每次对折后单个图形的面积都将减少为原来的一半，故单个图形的面积变化规律呈指数型变化—— $120\times {\left(\frac{1}{2}\right)}^{n-1}$ ，从而可以选用合适的数列模型—— $S_n=\frac{120\left(n+1\right)}{2^{n-1}}$ 来刻画对折 次后的图形面积总和。本题需要学生从问题情境中获取数学信息进行分析，从事实出发探寻一般规律，考查了逻辑推理素养，编码为R-S-1；学生需发现对折后图形面积的变化呈现一定规律，通过分析得出图形面积本质上是首项为120，公比为 $\frac{1}{2}$ 的等比数列，从而根据等比数列的相关知识建立相应的数列模型用于描述图像面积的总和，考查了学生的数学建模素养，编码为M-K-2。由于 $S_n=\frac{120\left(n+1\right)}{2^{n-1}}$ 是等差数列×等比数列结构，故在求对折n次后的图形面积总和时，可以针对性地选用错位相减法来进行求和计算，考查了学生的数学运算素养，编码为O-S-3。

例3 【解答题第20题】如图，在三棱锥A-BCD中，平面ABD $\perp$ 平面BCD， $AB=AD$ ，O为BD的中点。

(1) 证明： $OA\perp CD$ ；

(2) 若ΔOCD是边长为1的等边三角形，点E在棱AD上， $DE=2EA$ ，且二面角E-BC-D的大小为45˚，求三棱锥A-BCD的体积。

分析：1) 学生需从题目已给信息中推出 $OA\perp BD$ ，进而借助三棱锥直观地认识线面的位置关系，结合面面垂直的性质定理证得AO $\perp$ 平面BCD，由于CD $\subset$ 平面BCD，故根据线面垂直的性质定理可得到 $OA\perp CD$ ，考察了学生的直观想象和逻辑推理素养，编码为I-S-1，R-S-1。

2) 为了更直观地观察二面角E-BC-D，需在三棱锥中添加辅助线，进行视觉化表征，作 $EF\perp BD$ ， $FM\perp BC$ ，连接EM，形成 $\angle EMF$ ，这考查了学生的直观想象素养，编码为I-S-2。由于AO $\perp$ 平面BCD，故AO可作为三棱锥A-BCD的高，平面BCD可作为三棱锥A-BCD的底面。O为BD的中点，ΔOCD是边长为1的等边三角形，故ΔBCD为直角三角形，可得 $BC=\sqrt{3}$。 $\frac{DC}{FM}=\frac{BD}{BF}=\frac{2}{\frac{4}{3}}=\frac{3}{2}$ ，则 $FM=\frac{2}{3}$ ，由于 $\angle EMF={45}^{\circ }$ ，故 $EF=FM=\frac{2}{3}$ ，从而由 $\frac{AO}{EF}=\frac{DA}{DE}=\frac{3}{2}$ 可得 $AO=1$。解题过程中，学生需要利用线面垂直的判定定理和性质定理来证明所作的 $\angle EMF$ 即为面EBC和面BCD所形成的二面角，并且需要综合运用相似三角形的判定定理和性质定理求得AO的值，考查了逻辑推理素养，编码为R-K-2。最后计算三棱锥A-BCD的体积时，学生只需要识记三棱锥的体积公式 $V=\frac{1}{3}Sh$ (S表示底面积，h表示高)即可，考查了数学运算素养，编码为O-K-1。

3.1.2. 编码结果

对2021全国I卷的全部试题进行编码以后，可得到表4。

Table 4. Coding results of national volume I in 2021

表4. 2021全国I卷编码结果

3.2. 2021全国I卷对核心素养的考查情况

根据表3和2021全国I卷的编码结果可构建表5，由表5计算《课标》对各素养的要求占比与2021全国I卷对各素养的考查占比，可得到图1。计算示例：《课标》对数学抽象素养的要求占比 = 36/160 ≈ 22.5%，2021全国I卷对数学抽象素养的考查占比 = 6/61 ≈ 9.8%。

Table 5. Examination of mathematics core literacy of national volume I in 2021

表5. 2021全国I卷对数学核心素养的考查情况

Figure 1. Proportion of mathematics core literacy of national volume I in 2021

图1. 2021全国I卷对数学核心素养的考查占比

由图1我们可以看出2021全国I卷对逻辑推理素养的考查占比为32.8%，对数学运算素养的考查占比为36.1%，超过《课标》所要求的22.5%和13.1%。另外，该卷对数学抽象、数学建模、直观想象和数据分析素养的考查不达预期，没有满足《课标》的要求，其中数学建模和直观想象素养相较于《课标》的要求分别低了2.3%和7.3%，差异在10%以内；数学抽象和数据分析素养相较于《课标》的要求分别低了12.7%和10.9%，差异超出10%。

3.3. 2021全国I卷对核心素养三个维度的考查情况

根据表3和2021全国I卷的编码结果可构建表6，由表6计算《课标》对核心素养三个维度的要求占比2021全国I卷对核心素养三个维度的考查占比，可得到图2。计算示例：《课标》关于数学知识维度的要求占比 = 74/160 ≈ 46.3%，2021全国I卷关于数学知识维度的考查占比 = 30/61 ≈ 49.2%。

由图2我们可以看出2021全国I卷对数学知识维度的考查占比最高，达到了49.2%，另外该卷也集中考查了问题解决维度，占比为44.3%，试卷对这两个维度的考查均满足了《课标》的要求；然而数学思维维度的考查占比仅有6.6%，远不满足《课标》的要求。这说明2021全国I卷充分考查了学生对数学基础知识的掌握，注重考查学生在相关情境下利用数学知识进行问题分析和问题解决，强调知识的理解应用，但在知识拓展、知识创新等思维层面的考查仍有待加强。

Table 6. Examination of mathematics core literacy’s three dimensions of national volume I in 2021

表6. 2021全国I卷对数学核心素养三个维度的考查情况

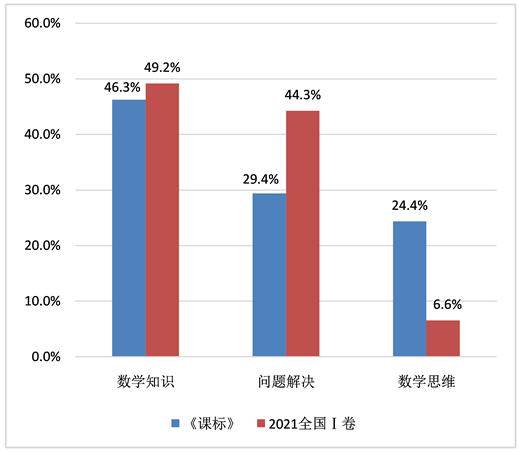
Figure 2. Proportion of mathematics core literacy’s three dimensions of national volume I in 2021

图2. 2021全国I卷对数学核心素养三个维度的考查占比

3.4. 2021全国I卷对核心素养三个水平的考查情况

根据表3和2021全国I卷的编码结果可构建表7，其中水平一综合了六大数学核心素养在数学知识、问题解决和数学思维三个维度的水平一，包括 $K_1,S_1,T_1$ ，其他水平亦是如此。由表7计算《课标》对核心素养三个水平的要求占比与2021全国I卷对核心素养三个水平的考查占比，可得到图3。计算示例：《课标》关于水平一的考查占比 = 56/160 ≈ 35.0%，2021高考数学I卷关于水平一的考查占比 = 22/61 ≈ 36.1%。

由图3可以发现2021全国I卷对数学学科核心素养不同水平的考查均有涉及，但考查占比有所差异，主要集中考查水平一和水平二，其中对水平二的考查占比为54.1%，相对于《课标》的要求而言属于超标型；对水平一的考查占比为36.1%，与《课标》要求的35.0%较为接近，属于相符型；对水平三的考查占比仅有9.8%，远不满足《课标》的要求，属于不足型。对此，2021全国I卷对于数学核心素养三个水平的考查可以总结为：考查以水平一为基础，以水平二为主，兼顾考查水平三。

Table 7. Examination of mathematics core literacy’s three levels of national volume I in 2021

表7. 2021全国I卷对数学核心素养三个水平的考查情况

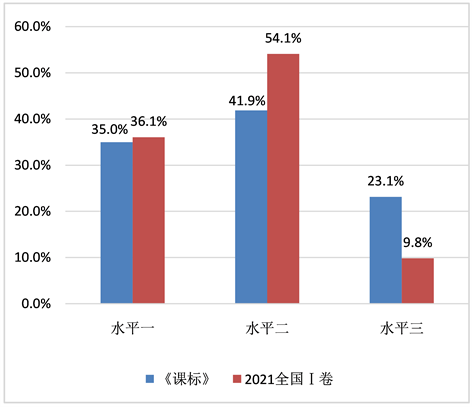
Figure 3. Proportion of mathematics core literacy’s three levels of national volume I in 2021

图3. 2021全国I卷数学核心素养三个水平的考查占比

4. 结论与启示

4.1. 结论

4.1.1. 2021全国I卷对各核心素养均有考查但分布不均

2021全国I卷对六大数学核心素养均作了考查，对高考要注重落实核心素养考查的要求做出了回应，但其考查分布不均，可大致分为三类：第一类是考查占比达到30%以上，满足条件的有逻辑推理和数学运算素养；第二类是考查占比在10%左右，有数学抽象和直观想象素养；第三类是考查占比在5%附近，有数学建模和数据分析素养。若将核心素养分为数学思维素养(数学抽象、直观想象)、数学方法素养(逻辑推理、数学运算)及数学工具素养(数学建模、数据分析) [10]，可以发现2021全国I卷对数学方法素养考查最多(68.9%)，数学思维素养次之(21.3%)，数学工具素养考查最少(9.8%)，考查分布差异较为明显。之所以数学方法素养的考查占比最大，是因为数学运算是按照公式法则来演算结果，逻辑推理则是按照逻辑来推导数学结论，两者在六大数学核心素养中具有基础地位 [10]。数学建模和数据分析作为现代信息技术社会中的关键能力和重要工具，在高考中的考查比例仍有待提高。

4.1.2. 2021全国I卷对数学思维维度和水平三层次的考查仍需加强

数学思维是用数学的观点去思考问题和解决问题的能力，在2021全国I卷的考查当中，数学思维维度的考查占比仅有6.6%，仍有很大的提高空间，试卷主要考查的是数学知识和问题解决维度，强调学生对数学基础知识和基本技能的掌握，这能够较好地把控试题难度，但不利于引导新课程背景下的课堂教学改革。在三个水平层次当中，水平二考查最多，水平一次之，水平三考查最少。《课标》综合六个数学学科核心素养水平的表现提出了数学学业质量水平，并指出数学学业质量水平二是高考的要求，也是数学高考的命题依据 [2]，我们可以发现2021全国I卷对数学学科核心素养的考查以水平二为主，这贴合了《课标》的要求。

4.2. 启示

4.2.1. 优化核心素养考查分配，加重数学工具素养考核

当今高考数学命题正在朝着数学核心素养的测评方向改革，数学核心素养是学生促进自身发展和适应信息化社会的关键能力，每一种素养对学生的个体发展都具有重要的作用。然而经过对2021全国I卷的研究分析，可以发现试卷对于核心素养的考查分配并不均匀，对数学工具素养(数学建模、数据分析)的考查较少。张奠宙等人曾建议把数学建模、数据处理和算法设计作为“新三大能力”，理由是“新三大能力”更契合当下的信息化社会和互联网时代，并且认为数据处理和数学建模两项关键能力就是为人工智能而准备的 [11]。如今的社会具备更强的现代性，信息技术发展迅速，对数据分析、数学建模素养的要求更甚，为了使教育更加契合社会发展的需要，后续的高考数学命题应基于《课标》的要求，立足于现实，适当加重对数学建模、数据分析素养的测查比例，优化对核心素养的考查。

4.2.2. 增强数学思维维度测查，提高水平三层次的考查

改进学生的常规思维和促进学生学习数学思维应当被看作是数学教育的一个基本目标，因此教师在展开教学之前应当深入思考教学内容所蕴含的数学思想和数学思想方法，要把促进学生思维的发展看作是教好数学的关键 [12]。高考数学试卷对于高中数学教学具有引领作用，因此为了更好地发挥高考的导向性，高考数学应当提升对数学思维维度的测查比重。今年是新高考数学I卷命题的第二年，继山东省之后，今年广东、福建、湖北、湖南、河北和江苏省也加入了使用新高考数学I卷的阵营，在探索文理不分科高考的初步阶段可以适当追求稳健，但在往后的高考数学命题当中，要在把控试题难度和提高数学思维考查之间寻求平衡，要在稳定的基础上追求适度创新，要统筹设置核心素养各水平间的梯度，适当加强对水平三的考查，要在保持传统命题的优秀理念的基础之上，积极融入落实核心素养考查的时代要求。