1. 引言
在大学物理的学习过程中,我们会遇到一大类本质上是求极值的问题,这类极值问题一般综合性比较强,因而具有一定的难度。因而学生遇到这类问题时往往无从下手,困扰着很多学生在普通物理中的学习。本文介绍变分方法以及利用变分方法来探讨这类极值问题的求解,不仅可以解决实际的物理问题,同时也可以培养学生的综合运用数学方法灵活解决问题的能力 [1] [2]。变分法是研究泛函极值的重要方法,掌握好这种方法,不仅能提高大学生的物理解题能力,同时对高中学生的物理学习也有借鉴意义 [3] [4] [5] [6]。接下来本文首先探讨三类可利用变分法解决的物理问题,然后对所涉及的变分问题做适当解析,最后对本文做一个系统总结。
2. 三类应用变分法的物理问题
2.1. 利用积分进行计算物理的极值问题
对于一般的大学物理问题,我们可以通过积分的形式算出相应的公式,函数极值的问题进行求解极值。
例1:半径为R的圆环,均匀带电,总电量为Q,求轴线上离圆心间距 处的电场强度,并求出x为多大时场强取得最大值。
解:如图1,在环上任取dl, P点场强为
由于环带电的对称性,
相互抵消,场强只有x分量,所以
,
考虑到
,所以
这里E沿x正轴方向,因为
,所以
为求极值条件,令
,则
解之得
,所以
。
又由于
。故
时,E取极大值。又因为这里只有一个极值点,因此这时E取最大值。
本例中,首先利用微元法和积分法给出电场强度E的函数表达式,这样问题就转化成求E的最大值问题,最后结合题目的实际意义,得到E的最大值点,从而完成对题目的求解。
2.2. 基于多元函数求极值的拉格朗日乘数法求解大学物理中的极值问题
例2::一个质量为m,所带电荷量为
的小球于重力场和电场强度为E且方向水平向左的匀强电场中,在一个光滑的半径为R圆形管道中 (管道厚度不计,且横截面的半径与小球的半径相同),在最高点以初速度v进行运动,现求出小球在管道何位置时势能最大。注意:小球初位置为
同时(
)
解:

Figure 2. Potential energy field in the pipeline
图2. 管道中的势能场
如图2,我们先建立坐标系,设小球在t时刻的位置为
首先小球的势能是电势能和重力势能的综合,且势能的减少量是功的增加量。所以这个问题转化为求功W的最大值。
此时W可以表示为
(1)
由题设可知:
(2)
于是问题转化成W在条件(2)限制下的极值问题:
(3)
(4)
(5)
(6)
求解上述方程组得到驻点
,因为在限制条件内只有一个驻点,该驻点为极值点,也为最值点。
在该点处所做功最小为
,其势能最大。
拉格朗日乘数法是条件极值问题的一个重要方法,也是解决约束变分问题的一个重要方法。结合上例,可以看出利用拉格朗日乘数法求解极值问题首先要根据实际问题给出目标函数,然后再根据实际问题给出对变量的限制条件,并求解目标函数对各个变量的偏导数为零的点,最后需要判别求解出来的这些点是不是所要求的极值点,这是拉格朗日乘数法的一个难点,不过在很多情形下,结合实际题目的意义就可以判别这些点是否是极值点,上例就属于这种情况。
2.3. 利用欧拉–拉格朗日方程进行对物理运动方程进行求解
欧拉–拉格朗日方程是经典力学里的重要方程,在大学物理有不少应用,为此我们首先给出以下几个定义。
定义1 (拉格朗日函数) [7] 格朗日函数表示为
其中
表示拉格朗日量,T为动能,V为势能。
在分析力学里,一个动力系统的拉格朗日函数,是描述整个物理系统的动力状态的函数。假设已知一个系统的拉格朗日函数,则可以将拉格朗日量直接代入拉格朗日方程,稍加运算,即可求得此系统的运动方程。
定义2 (哈密顿原理) [8] 对于任何有势力作用下的完整的系统的质点系,在给定始点
和终点
的状态后,其真实运动与任何容许运动的区别是真实运动使泛函
达到极值,也便是
其中
是定义1中的拉格朗日函数。
定义3 (自由度)
确定某物体空间位置所需要的独立坐标的数目
,称作物体的自由度数,可分为平动自由度,转动自由度等。
例如,图3球体的平动自由度
,平动轴为
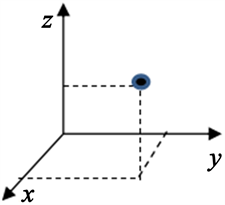
Figure 3. Degrees of freedom in three-dimensional space
图3. 三维空间的自由度
定义4 (广义坐标系)广义坐标即能够唯一确定系统位形的独立坐标。
例如,二维平面下的单摆,单摆线(线长为l)和铅垂线的夹角
即是一个广义坐标,亦或者选取笛卡尔坐标系来描述单摆,则x可以说成是一个广义坐标,因为此时y可以用x轴来导出,并且此时y用x的表出是唯一的(
)。但此时不可用y作为一个广义坐标,因为x用y的表出不唯一(
)。
定义5 (广义力) [9] [10] 广义力
是光义坐标
对应的力,其量纲由广义力与广义坐标的虚位移(即无穷小位移)的乘积决定的。
若一个系统的状态可以由几个独立的广义坐标
和时间t的函数描述,则广义坐标关于时间的函数可通过拉格朗日方程解出,即在一般情况下,拉格朗日方程可表达为
其中
表示对应
的广义力,
。
在N小于3n的情况下(n为系统质点数),即广义坐标个数比x坐标少,拉格朗日方程表示为
该方程也称作保守系统的拉格朗日方程。这里
表示为
对时间t的一阶导函数。
有了以上这些概念后,接下来通过几个例子来说明这些概念在解决大学物理中的问题的应用。
例3:质量为m,半径为r的圆柱体在一空心圆柱体体内的内表面上做纯滚动运动。空心圆柱体的质量为M,半径为R,可绕中心水平轴O转动,两圆柱体均系均质,求系统的运动微分方程组。
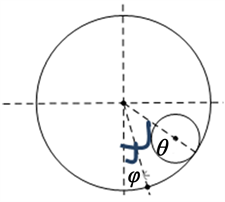
Figure 4. Motion of small cylinder in hollow cylinder
图4. 空心圆柱中小圆柱体的运动
解:系统的自由度
,如图4所示,取空心圆柱体的转角
和两圆柱体的中心连线的转角
为广义坐标。这里空心圆柱体的转角
和两圆柱体的中心连线的转角
均是关于时间t的函数
易得圆柱体滚动得转动惯
,设圆柱体得角速度为
。
圆柱体的中心速度为
圆柱体的角速度为
空心圆柱的边缘线速度
且系统的动能为
将v1,
,v代入可得,系统动能
系统势能
从而得到拉格朗日函数
计算
,
从而计算各偏导数,得到
将上式代入拉格朗日方程并化间即可得到系统得运动微分方程组为
,
。
例4:椭圆摆由质量为
的物块和质量为
的单摆组成,物块可在光滑的水平面上滑动,摆臂长度为L,摆臂的质量可忽略不计,用光滑铰链连接在物块上,求系统的运动方程。
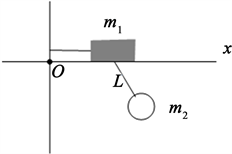
Figure 5. Motion of an elliptical pendulum
图5. 椭圆摆的运动
解:取Ox轴的x和摆的转角
为广义坐标,如图5所示,则
物体的动能为
,
单摆的动能为
则系统的动能为
系统的势能为
从而系统的拉格朗日函数
求各导数,得到
将上面各式代入拉格朗日方程,即可得到系统的运动方程
拉格朗日方程是经典力学描述物体运动的一个重要方程,比如在动力系统的研究中经常会用到拉格朗日方程。从上面两个例子可以看出,拉格朗日方程在普通物理的学习中也有广泛的应用,掌握好这个方程的相关概念和用法,对我们学好普通物理大有裨益。
3. 小结
通过上述例子可以看出,大学物理中很多问题都可以转化成数学中的极值问题进行求解,也就是利用变分方法来解决这类问题。利用变分方法求解这类问题的一个重要步骤是根据所给问题找出目标函数的表达式以及函数中变量的变化范围,然后就可以把问题转化成数学中函数的极值问题了。经常这样训练,一方面可以提升我们对物理现象的理解,同时也加强我们对数学工具的应用能力,进而提高自身的综合能力。
基金项目
南京信息工程大学大学生创新创业训练项目(XJDC202110300415)。