基于自变权的CNN & LSTM组合PM_2.5浓度预测——以北京为例

Combined PM_2.5 Concentration Prediction Model Based on CNN & LSTM of Variable Weight—A Case Study of Beijing

摘要: 本文基于CNN和LSTM神经网络模型，构建自变权的CNN & LSTM组合模型。首先分析污染物因子和气象因子与PM_2.5的相关性，确定PM_2.5浓度的预测因子，再对数据进行标准化预处理，用CNN模型和LSTM模型分别进行预测，最后，采用基于自变权的CNN & LSTM组合模型进行预测，并比较不同模型的预测效果。结果表明：1) PM_2.5浓度与空气污染物(PM₁₀, SO₂, NO₂, CO, O3)之间的相关性总体高于PM_2.5浓度与气象因子变量(温度、湿度、风速、气压、降水量)之间的相关性，其中NO₂与PM_2.5相关性最强，降水量与PM_2.5相关性最弱；2) CNN-LSTM (variable)模型的预测结果优于LSTM、CNN、CNN-LSTM (equal)、CNN-LSTM (residual)模型；3) CNN-LSTM (variable)模型的RMSE、MAE和MAPE的值分别为2.07%、9.66%和8.66%。

Abstract: An adaptive weighting method based on CNN and LSTM was designed to build a combined CNN model and LSTM network with variable weights. Firstly, analyze the correlation between pollutant factors and meteorological factors and PM_2.5, and determine the predictive factors of PM_2.5 concentration. Then, the preprocessed data sets were input into CNN model and LSTM model for prediction respectively. Finally, the CNN & LSTM combined model based on the variable weight is used for prediction, and the prediction effects of different models are compared. The results show that: 1) The correlation between pollutant variables and PM_2.5 is generally higher than that between meteorological variables and PM_2.5, in which NO₂ is the strongest correlation with PM_2.5 and precipitation is the weakest correlation with PM_2.5; 2) The prediction results of the CNN-LSTM (variable) model are better than those of the LSTM, CNN, CNN-LSTM (equal) and CNN-LSTM (residual) models; 3) The values of RMSE, MAE and MAPE for CNN-LSTM (variable) model are 2.07%, 9.66% and 8.66%, respectively.

1. 引言

PM_2.5 (fine particulate matter)是悬浮于大气中的一种细颗粒物，根据空气动力学当量直径指标，PM_2.5是指当量直径小于等于2.5 μm的细颗粒物 [1]，PM_2.5是雾霾的主要组成成分，将对空气质量造成巨大影响。同时，PM_2.5也会对人类的出行造成一定的困扰，甚至危害人类身心健康 [2]。社会经济快速发展的同时，随之而来的是环境污染问题，其中雾霾污染问题不容小视。近年来，由PM_2.5造成的空气污染问题已经引起了国家和政府以及社会的重视 [3]。一些研究表明，一些疾病的发生以及死亡都与PM_2.5污染有着显著相关关系 [4]。因此，PM_2.5的预测和预警至关重要，意义非凡。

Mishra等 [5] 利用Neuro-Fuzzy模型预测印度德里市区的雾霾；Wang等 [6] 利用新一代天气研究预测和化学模式WRF-Chem对长三角地区城市空气质量和区域雾霾污染进行预测；杜续等 [7] 利用随机森林回归算法设计PM_2.5浓度预测模型，对西安市气象数据进行实证分析，结果表明，与BP神经网络模型相比，该模型的预测精度更高；Liu等 [8] 通过自回归移动平均模型(ARIMA)、人工神经网络(ANNs)模型和指数平滑法(ESM)预测PM_2.5浓度；李芬等 [9] 对天气类型进行聚类分析，建立不同天气类型下的PM_2.5浓度短期预测模型；于伸庭等 [10] 构建LSTM-CNN组合模型，预测未来6小时PM_2.5浓度；刘旭林等 [11] 提出了一种基于CNN和Seq2Seq的深度学习模型，对北京市PM_2.5浓度进行实证分析；艾洪福等 [12] 建立了BP神经网络预测模型，对长春市的PM_2.5浓度进行预测；张浩等 [13] 利用广义隐马尔可夫模型，对北京市11个站点的PM_2.5浓度数据进行实证分析；谢崇波等 [14] 基于遗传算法，采用门控循环单元，建立神经网络混合模型，预测绵阳市PM_2.5浓度。先前很多研究多只考虑空气污染物对PM_2.5浓度预测的影响，常常忽略气象因子对PM_2.5浓度的影响，或未考虑预测因子与PM_2.5之间的非线性关系。本研究利用北京市PM_2.5浓度历史数据、空气污染物数据以及气象因子数据，设计基于自变权的CNN & LSTM组合预测模型。

2. 研究区域和数据

2.1. 研究区域

北京市(39˚26'~41˚03'N，115˚25'~117˚30'E)位于中国华北地区，面积约16,410 km²，常住人口达2189.31万，属于暖温带半湿润半干旱季风气候。北京是中国首都，同时也是我国经济、文化、产业发展的中心，其空气质量一直备受关注。

2.2. 数据来源

研究数据包括污染物浓度数据(PM_2.5, PM₁₀, SO₂, NO₂, CO, O₃)和气象因子数据(温度、湿度、风速、气压、降水量)，其中污染物浓度数据来源于中国环境监测总站的全国城市空气质量实时发布平台(https://quotsoft.net/air/)，气象因子数据来源于国家气象信息中心中国气象数据网(http://data.cma.cn/)。

2.3. 数据统计与分析

本研究选取北京市的空气污染物浓度小时数据和气象数据，时间范围为2021年1月1日~2021年7月31日，共5088组数据，统计性描述如表1所示。由于获取的数据会存在个别缺失的情况，本研究通过填补方式进行缺失值补充，采用缺失值前1小时与后1小时的均值进行填补。

Table 1. Statistical description of data set variables

表1. 数据集变量统计性描述

3. 研究方法

3.1. 相关性分析

相关性分析是分析两个或两个以上变量的线性相关程度 [15]。Pearson 相关系数的计算公式为：

${\rho }_{X,Y}=\frac{\mathrm{cov}\left(X,Y\right)}{{\sigma }_X{\sigma }_Y}=\frac{E\left(\left(X-{\mu }_X\right)\left(Y-{\mu }_Y\right)\right)}{{\sigma }_X{\sigma }_Y}$ (1)

式中， $\rho$ 为变量 $X,Y$ 之间的相关系数， ${\mu }_X,{\mu }_Y$ 分别为 $X,Y$ 的均值， ${\sigma }_X,{\sigma }_Y$ 分别为 $X,Y$ 的方差。

3.2. CNN

20世纪60年代，Hubel和Wiesel [16] 提出了卷积神经网络(convolutional neural networks, CNN)，起初CNN主要应用于图像特征的提取与分类 [17]，随着学者们的不断研究，发现CNN同样可以应用于时间序列数据分析 [18]。

3.3. LSTM

LSTM (Long Short-Term Memory)是由Hpchreiter和Schmidhuber [19] 在1997年提出的，LSTM神经网络模型结构如图1所示：

Figure 1. LSTM model structure

图1. LSTM模型结构

其计算公式如下：

$f_t=\sigma \left(w_f\cdot \left[h_{t-1},X_t\right]+b_f\right)$ (2)

$i_t=\sigma \left(w_i\cdot \left[h_{t-1},X_t\right]+b_i\right)$ (3)

${C^{\prime }}_t=\tanh \left(w_c\cdot \left[h_{t-1},X_t\right]+b_c\right)$ (4)

$C_t=f_t\times C_{t-1}+i_t\times {C^{\prime }}_t$ (5)

$o_t=\sigma \left(w_o\cdot \left[h_{t-1},X_t\right]+b_o\right)$ (6)

$h_t=o_t\times \tanh \left(C_t\right)$ (7)

式中， $f_t$ 为遗忘门的向量值， $i_t$ 为输入门的向量值， ${C^{\prime }}_t$ 和 $C_t$ 分别为上一时刻和当前时刻记忆单元的向量值， $o_t$ 为输出门的向量值， $h_t$ 表示t时刻单元输出， $X_t$ 表示t时刻的输入。w和b在训练过程中会不断更新，分别表示权重和偏置项， $\sigma$ 和tanh是激活函数。

3.4. 组合预测模型

3.4.1. 等值赋权及残差赋权组合模型

等值赋权组合模型即赋予每个单模型相同的权重，而残差赋权组合模型各权重可由下式计算得出：

$f\left(X_t\right)=\frac{1}{n}{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\omega }_i}\left(t-1\right)f_i\left(X_t\right)$ (8)

${\omega }_i\left(t\right)=\frac{\frac{1}{{\bar{\epsilon }}_l\left(t-1\right)}}{{\displaystyle {\sum }_{i=1}^n\frac{1}{{\bar{\epsilon }}_l\left(t-1\right)}}}$ (9)

$\text{s}\text{.t}.{\displaystyle {\sum }_{i=1}^n{\omega }_i}\left(t-1\right)=1,{\omega }_i\left(t-1\right)\ge 0$ (10)

其中， ${\omega }_i\left(t-1\right)$ 为 $t-1$ 时刻第i个模型的权重， ${\bar{\epsilon }}_l\left(t-1\right)$ 为 $t-1$ 时刻第i个模型的预测误差绝对值。

3.4.2. 自变权组合模型

在残差赋权组合模型的基础上，权重不再保持不变，当前时刻的权重为前m个时刻的权重平均值，并比较权重改变前后预测效果(本文m取3)：

${\omega }_j\left(t\right)=\frac{1}{m}{\displaystyle \underset{k=1}{\overset{m}{\sum }}{\omega }_j}\left(t-k\right)$ (11)

对于t时刻，残差赋权组合模型和自变权组合模型的预测值与真实值的误差绝对值分别为 $e_{i,t}$ 和 $e_{j,t}$，即：

$e_{i,t}=\left|{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\omega }_i}\left(t\right)f_i\left(X_t\right)-f\left(t\right)\right|$ (12)

$e_{j,t}=\left|{\displaystyle \underset{j=1}{\overset{n}{\sum }}{\omega }_j}\left(t\right)f_j\left(X_t\right)-f\left(t\right)\right|$ (13)

比较两者的大小，若 $e_{i,t}>e_{j,t}$，则说明该时刻自变权组合模型预测效果更优，故使用新权重，反之，则仍保持原先权重。

3.5. 预测流程

预测流程如图2所示。

1) 数据预处理

对原始数据的缺失值进行填充处理以及标准化处理。

2) 单模型预测

将数据集按照8:2的比例划分为训练集和测试集，将训练集分别输入CNN和LSTM模型中，确定最优模型，再对测试集进行预测。

3) 自变权组合模型预测

基于第2)步CNN和LSTM模型的预测结果，采用3.4节所述赋权方法，依次构建等值赋权组合模型CNN-LSTM (equal)，残差赋权组合模型CNN-LSTM (residual)和自变权组合模型CNN-LSTM (variable)，并进行预测。

4) 模型评价分析

计算各评价指标，对个模型进行预测效果比较。

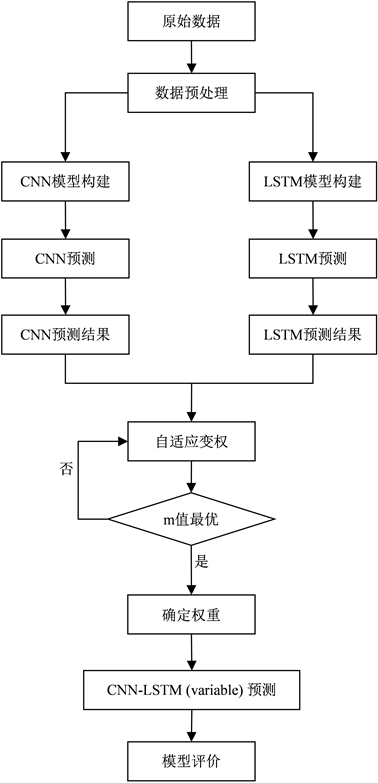
Figure 2. CNN-LSTM (Variable) model prediction flow

图2. CNN-LSTM (Variable)模型预测流程

3.6. 评价指标

为进行模型精度的比较，本研究采用评价指标：均方根误差(RMSE)，平均绝对误差(MAE)和平均绝对百分比误差(MAPE)，相应的计算公式为：

$\text{RMSE}=\sqrt{\frac{1}{n}{\displaystyle \underset{t=1}{\overset{n}{\sum }}{\left(y_t-{\hat{y}}_t\right)}^2}}$ (14)

$\text{MAE}=\frac{1}{n}{\displaystyle \underset{t=1}{\overset{n}{\sum }}\left|y_t-{\hat{y}}_t\right|}$ (15)

$\text{MAPE}=\frac{100}{n}{\displaystyle \underset{t=1}{\overset{n}{\sum }}\left|\frac{y_t-{\hat{y}}_t}{y_t}\right|}$ (16)

式中，n为样本量， $y_t$ 为真实值， ${\hat{y}}_t$ 为其预测值。误差越小，则表示预测精度越高，预测效果越好，模型性能越好。

4. 结果与讨论

4.1. PM_2.5现状分析

如图3及表2所示，2021年1月至7月，3月PM_2.5月均浓度最高，为83.54 μg/m³，其中3月15日9时PM_2.5浓度最高，为448 μg/m³，3月15日平均浓度为208 μg/m³。2021年3月PM_2.5浓度突然升高，主要是受北京当月沙尘暴影响。6月~7月，PM_2.5小时浓度均低于70 μg/m³，6月和7月PM_2.5小时浓度最高分别为65 μg/m³和43 μg/m³，最低小时浓度均为2 μg/m³，而7月PM_2.5月均浓度是该年1月~7月中最低的，为15.97 μg/m³。此外，2月PM_2.5日均最高浓度为205 μg/m³，PM_2.5小时最高浓度达289 μg/m³，仅次于3月。

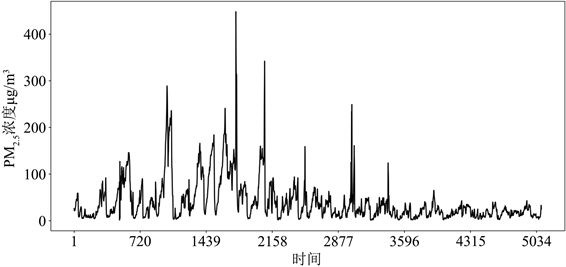
Figure 3. Change in hourly PM_2.5 concentrations January 2021~July 2021

图3. 2021年1月~2021年7月PM_2.5小时浓度变化

Table 2. 2021.1.1~2021.7.31 PM2.5 daily and monthly average concentration

表2. 2021.1.1~2021.7.31 PM_2.5浓度日均浓度及月均浓度情况

4.2. 预测因子分析

4.2.1 . PM_2.5与空气污染物相关性分析

首先，探索PM_2.5浓度与其它空气污染物因子(PM₁₀, SO₂, NO₂, CO, O₃)之间的关系，散点图如图4所示。

如图4所示，PM_2.5与其他空气污染物之间均存在一定的相关关系。其中 PM₁₀、NO₂与PM_2.5之间的相关关系较强，而SO₂、CO与PM_2.5之间的相关关系较弱。

综合表3分析，确定预测因子为SO₂，NO₂，CO和O₃。其中，PM₁₀与PM_2.5有着极强相关性，不将其放入预测因子中。

Table 3. Correlation coefficients between PM2.5 concentrations and air quality factors

表3. PM_2.5浓度与空气质量因素相关系数

Figure 4. Correlation analysis of PM_2.5 and air pollutants

图4. PM_2.5与空气污染物的相关性分析

4.2.2 . PM_2.5与气象因子相关性分析

大量研究表明，气象因子也对PM_2.5浓度有重要影响 [20] [21] [22] [23]。利用研究区域PM_2.5浓度和气象因子数据，计算它们之间的Pearson相关系数，进行相关性分析。如表4所示，PM_2.5浓度与本研究所选的气象因子之间均存在一定的相关性，其中，PM_2.5与温度、湿度、风速和降水量均呈负相关关系，仅与气压呈正相关关系。

Table 4. Correlation coefficients between PM2.5 concentrations and meteorological factors

表4. PM_2.5浓度与气象因子相关系数

4.3. 预测分析与对比

本研究构建基于自变权的CNN & LSTM组合模型，以北京为研究区域，对未来1小时PM_2.5浓度进行短期预测。图5给出了LSTM、CNN、等值赋权组合模型CNN-LSTM (equal)、残差赋权组合模型CNN-LSTM (residual)、自变权组合模型CNN-LSTM (variable)各自的预测结果。由图5可知，组合模型的预测效果优于单机器学习模型的预测效果，其中，基于自变权的CNN&LSTM组合模型预测效果最好，预测精度最高，预测值与真实值偏差最小。

如表5所示，LSTM模型的评价指标数值分别为RSME为9.39，MAE为10.58，MAPE为22.33%；CNN模型的评价指标数值分别为RSME为5.11，MAE为10.20，MAPE为32.49%；而等值赋权组合模型CNN-LSTM (equal)的评价指标数值分别为RSME为3.08，MAE为9.83，MAPE为19.06%；残差赋权组合模型CNN-LSTM (residual)的评价指标数值分别为RSME为2.10，MAE为9.71，MAPE为8.81%；自适应变权组合模型CNN-LSTM (variable)的评价指标数值分别为RSME为2.07，MAE为9.66，MAPE为8.66%。改进的自适应变权组合模型相较于传统等值赋权模型CNN-LSTM (equal) RSME提升了32.8%，MAE提升了1.2%，MAPE提升了54.5%。

Figure 5. Predicted and true values for each model

图5. 各模型预测值和真实值

Table 5. Comparison of the prediction accuracy of different evaluation indicators

表5. 不同评价指标的预测精度比较

5. 结论

本研究基于CNN模型和LSTM网络进行一定改进得到自变权组合的PM_2.5浓度预测方法，该组合模型考虑了时间序列的相互关系，同时考虑了PM_2.5浓度与预测因子之间的非线性关系。研究发现：

1) 2021年1月至7月，3月PM_2.5月均浓度最高，7月PM_2.5月均浓度最低。其中3月15日9时PM_2.5浓度最高，为448 μg/m³，3月15日平均浓度为208 μg/m³。

2) 由相关性分析可知，PM_2.5浓度与空气污染物(PM₁₀, SO₂, NO₂, CO, O₃)之间的相关性总体高于PM_2.5浓度与气象因子变量(温度、湿度、风速、气压、降水量)之间的相关性，其中NO₂与PM_2.5之间是相关系数为0.5193，相关性最强，降水量与PM_2.5相关性最弱，相关系数为−0.0473。

3) 本研究构建的基于自变权的CNN & LSTM组合PM_2.5预测模型考虑了数据的时间序列以及非线性特征。与单一的机器学习模型以及传统组合模型相比，该模型与真实值的拟合效果更好，偏差较小。

基金项目

国家社会科学基金重大项目“大数据时代雾霾污染经济损失评估及防治对策研究”(17ZDA092)。

NOTES

^*通讯作者。