在媒体报道影响下具有隔离项的传染病模型的动力学分析

Dynamics of an SIQS Epidemic Model with Media Coverage

摘要: 本文采用分段光滑函数作为媒体影响函数引入到具有隔离项的SIQS传染病模型中，首先，得到平衡点的表达式，然后在R₀ < 1和R₀ > 1时分别分析平衡点的局部稳定性和全局稳定性。最后，利用数值模拟验证平衡点的全局稳定性并说明媒体报道和隔离策略的有效性。

Abstract: In this paper, the piecewise smooth function is used as the media influence function to SIQS infectious disease model. First, we get the expression of the equilibrium point, and then analyze the local stability and global stability of the equilibrium point respectively in R₀ < 1 and R₀ > 1. Finally, we use numerical simulation to verify the global stability of the equilibrium point and illustrate the effectiveness of media coverage and quarantine strategies.

1. 引言

当一种新型传染病暴发时，由于其突发性与不确定性，人们对其缺乏认识，也没有相应的药物和疫苗，因此，在突发性传染病暴发的初期，非药物的防控策略在抑制疾病传播方面是十分重要的 [1]。常见的非药物防控策略有媒体报道和隔离策略 [2] [3] [4]。媒体报道通过网络媒体宣传进而改变个人行为习惯来预防感染，例如戴口罩、减少外出、频繁洗手等。特别是在新冠肺炎(covid-19)期间，公共媒体通过电视、互联网、微信公众号等多途径报道疫情最新消息，同时宣传疾病感染的常见症状和有效的预防措施(保持社交距离，戴口罩，减少不必要的出行，不到人口密集的公共场所聚集等)，使得人们加强自身防范来减少感染率 [5] [6]。近年来，很多学者都将媒体报道引入到传染病模型中，并分析媒体报道对传染病感染率产生的影响 [2] [7] [8] [9]。 [10] 中在SEI模型中引入媒体报道的影响，其媒体报道函数为 $\mu {\text{e}}^{-mI}$。 [11] 中在SIS模型中引入函数 ${\beta }_1-{\beta }_{2}f\left(I\right)$ 作为媒体报道函数。 [12] 中考虑带有媒体影响的SIR模型，其媒体报道函数为 $f\left(I\right)={\text{e}}^{-mI}$， $0<I\le I_c$， $f\left(I\right)={\text{e}}^{-m{I}_c}$， $I>I_c$。在 [13] 中用 $\exp \left(-\epsilon \alpha I\right)$ 来表示媒体报道函数，讨论媒体报道对疾病传染的影响。在没有疫苗的情况下，隔离策略是抑制疾病传播的最有效方式，隔离策略可以减少易感者与感染者接触的频率和概率，并使疫情在短时间内得到有效控制 [3] [4]。很多学者都研究过具有隔离项的传染病模型 [3] [4] [5] [14]，隔离策略在新冠肺炎(covid-19)的防治中也是一个十分有效的防治策略 [15]。

在 [12] 的启发下，本文建立了一个在媒体报道影响下具有隔离项的传染病模型，用分段光滑函数表示媒体报道影响，当感染者比例I超过临界值 $I_c$ 时媒体报道将发挥作用，并对疾病传播产生影响。在第2节中得到在媒体报道影响下的SIQS模型的平衡点；在第3节中对平衡点进行局部稳定性分析；第4节中对平衡点进行全局稳定性分析；最后，在第5节对模型进行数值模拟，说明媒体报道作用和隔离率 $\delta$ 对抑制感染者增加有显著影响。

2. 模型建立

我们建立在媒体报道影响下的SIQS模型，令 $S\left(t\right),I\left(t\right),Q\left(t\right)$ 分别表示易感者，感染者和隔离者相对于人口总数的比例。假设人口总数不变， $S+I+Q=1$。我们令分段光滑函数

$f\left(I\right)=\{\begin{array}{l}1,I\le I_c\\ {\text{e}}^{-m\left(I-I_c\right)},I>I_c\end{array}$ (1)

表示媒体报道影响，其中m是影响因子， $m>0$， $I_c$ 是感染者的临界值， $f\left(I\right)$ 表示媒体报道只有在I超过 $I_c$ 时才起作用，我们把媒体报道影响引入到SIQS模型中，如下：

$\{\begin{array}{l}{S}^{\prime }=\mu -\beta f\left(I\right)SI-\mu S+\gamma I+\epsilon Q\\ I^{\prime }=\beta f\left(I\right)SI-\left(\mu +\delta +\gamma \right)I\\ Q^{\prime }=\delta I-\left(\epsilon +\mu \right)Q\end{array}$ (2)

其中， $\mu$ 是自然出生率和死亡率， $\beta$ 是感染率， $\delta$ 是隔离率， $\gamma$ 和 $\epsilon$ 分别是从感染者I和隔离者Q恢复到易感者S的恢复率。显然， $R_{+}^3=\left\{\left(S,I,Q\right)|S\ge 0,I\ge 0,Q\ge 0\right\}$ 是正不变集。易得 $\frac{\text{d}S}{\text{d}t}+\frac{\text{d}I}{\text{d}t}+\frac{\text{d}Q}{\text{d}t}=0$，并且 $Q=1-S-I$， $Q\ge 0$， $S+I\le 1$。因此，我们只考虑(2)中前两个方程

$\{\begin{array}{l}{S}^{\prime }=\mu -\beta f\left(I\right)SI-\mu S+\gamma I+\epsilon \left(1-S-I\right)\\ I^{\prime }=\beta f\left(I\right)SI-\left(\mu +\delta +\gamma \right)I\end{array}$ (3)

进而在可行域 $\Gamma$ 中研究模型(3)。

$\Gamma =\left\{\left(S,I\right)\in R_{+}^2|S+I\le 1\right\}$

其中 $R_{+}^2=\left\{Z=\left(S,I\right)|S\ge 0,I\ge 0\right\}$， $\Gamma$ 对于模型(3)是正不变集。令 $H\left(Z\right)=I-I_c$，其中 $Z={\left(S,I\right)}^{\text{T}}$，且

$F_{G1}\left(Z\right)={\left(\mu -\beta SI-\mu S+\gamma I+\epsilon \left(1-S-I\right),\beta SI-\left(\mu +\delta +\gamma \right)I\right)}^{\text{T}}$

$F_{G2}\left(Z\right)={\left(\mu -\beta {\text{e}}^{-m\left(I-I_c\right)}SI-\mu S+\gamma I+\epsilon \left(1-S-I\right),\beta {\text{e}}^{-m\left(I-I_c\right)}SI-\left(\mu +\delta +\gamma \right)I\right)}^{\text{T}}$

根据 [12]，我们将模型(3)可写成如下非光滑系统

$\stackrel{\dot{}}{Z}\left(t\right)=\{\begin{array}{l}{F}_{G1}\left(Z\right),Z\in G_1\\ F_{G2}\left(Z\right),Z\in G_2\end{array}$ (4)

其中 $G_1=\left\{Z\in R_{+}^2|H\left(Z\right)\le 0\right\}$， $G_2=\left\{Z\in R_{+}^2|H\left(Z\right)>0\right\}$。两个区域 $G_1$ 和 $G_2$ 的切换面为， $\Sigma =\left\{Z\in R_{+}^2|H\left(Z\right)=0\right\}$。因此，称系统 $S_{G1}$ 为非光滑系统(4)在区域 $G_1$ 上的部分，称系统 $S_{G2}$ 为非光滑系统在区域 $G_2$ 上的部分。

系统 $S_{G1}$ 的平衡点和基本再生数

系统 $S_{G1}$ 为

$\{\begin{array}{l}{S}^{\prime }=\mu -\beta SI-\mu S+\gamma I+\epsilon \left(1-S-I\right)\\ I^{\prime }=\beta SI-\left(\mu +\delta +\gamma \right)I\end{array}$ (5)

令 $S^{\prime }=0,I^{\prime }=0$ 求解平衡点，得到系统 $S_{G1}$ 有两个平衡点，分别为无病平衡点 $P_0=\left(1,0\right)$ 和地方病平衡点 $P_1$。

$P_1=\left(S_1,I_1\right)=\left(\frac{\mu +\delta +\gamma }{\beta },\frac{\left(\mu +\epsilon \right)\left(1-1/R_0\right)}{\mu +\delta +\epsilon }\right)$

并通过 $S_1$ 求出基本再生数 $R_0$，即：

$R_0=\frac{\beta }{\mu +\delta +\gamma }$.

定理1 如果 $R_0<1$，那么系统(5)在 $\Gamma$ 中只有无病平衡点 $P_0=\left(1,0\right)$。如果 $R_0>1$，那么系统(5)有两个平衡点：无病平衡点 $P_0$ 和地方病平衡点 $P_1=\left(S_1,I_1\right)$。

系统 $S_{G2}$ 的平衡点和阈值参数

系统 $S_{G2}$ 为

$\{\begin{array}{l}{S}^{\prime }=\mu -\beta {\text{e}}^{-m\left(I-I_c\right)}SI-\mu S+\gamma I+\epsilon \left(1-S-I\right)\\ I^{\prime }=\beta {\text{e}}^{-m\left(I-I_c\right)}SI-\left(\mu +\delta +\gamma \right)I\end{array}$ (6)

也令 $S^{\prime }=0,I^{\prime }=0$ 得到系统 $S_{G2}$ 的两个平衡点 [15] [16]：无病平衡点 ${P^{\prime }}_0$ 和地方病平衡点 $P_2$

${P^{\prime }}_0=\left(1,0\right),P_2=\left(S_2,I_2\right)$

其中

$S_2=\frac{\mu +\delta +\epsilon }{m\left(\mu +\epsilon \right)}W\left(\frac{m\left(\mu +\epsilon \right)\left(\mu +\delta +\gamma \right)}{\beta \left(\mu +\delta +\epsilon \right)}{\text{e}}^{-m{I}_c+\frac{m\left(\mu +\epsilon \right)}{\mu +\delta +\epsilon }}\right)$

$I_2=\frac{\mu +\epsilon }{\mu +\delta +\epsilon }-\frac{1}{m}W\left(\frac{m\left(\mu +\epsilon \right)\left(\mu +\delta +\gamma \right)}{\beta \left(\mu +\delta +\epsilon \right)}{\text{e}}^{-m{I}_c+\frac{m\left(\mu +\epsilon \right)}{\mu +\delta +\epsilon }}\right)$

定理2 如果 $R_c<1$，那么系统(6)在 $\Gamma$ 中只有无病平衡点 ${P^{\prime }}_0=\left(1,0\right)$。如果 $R_c>1$，那么系统(6)有两个平衡点：无病平衡点 ${P^{\prime }}_0$ 和地方病平衡点 $P_2=\left(S_2,I_2\right)$。

证明：注意到 $P_2$ 并不总是在可行域 $\stackrel{。}{\Gamma }$，所以当 $I_2>0$ 时，即 $\frac{\beta {\text{e}}^{m{I}_c}}{\mu +\delta +\gamma }>1$， $P_2$ 存在并有意义.而当 $\frac{\beta {\text{e}}^{m{I}_c}}{\mu +\delta +\gamma }<1$ 时，即 $R_0<{\text{e}}^{-m{I}_c}<1$，只有 ${P^{\prime }}_0$ 存在。

令 $R_c=\frac{\beta {\text{e}}^{m{I}_c}}{\mu +\delta +\gamma }$ 是系统(6)的阈值参数。

3. 局部渐近稳定性

3.1. 系统S_G1的局部渐近稳定性

定理3 对于系统 $S_{G1}$，当 $R_0<1$ 时，无病平衡点 $P_0$ 是局部渐近稳定的。当 $R_0>1$ 时， $P_1$ 是局部渐近稳定的， $P_0$ 是不稳定的。

证明：系统 $S_{G1}$ 在 $P_0$ 处的Jacobian矩阵

$J\left(P_0\right)=\left[\begin{array}{cc}-\mu -\epsilon & -\beta +\gamma -\epsilon \\ 0& \beta -\left(\mu +\delta +\gamma \right)\end{array}\right]$

我们得到平衡点 $P_0$ 的特征方程为

$\left(\lambda +\mu +\epsilon \right)\left(\lambda -\beta +\mu +\delta +\gamma \right)=0$

故当 $R_0<1$ 时，该特征方程具有两个负特征值，这表明当 $R_0<1$ 时，无病平衡点 $P_0$ 是局部渐近稳定的。当 $R_0>1$ 时， $P_0$ 是不稳定的。

系统 $S_{G1}$ 在 $P_1$ 处的Jacobian矩阵

$J\left(P_1\right)=\left[\begin{array}{cc}-\beta I_1-\mu -\epsilon & -\beta S_1+\gamma -\epsilon \\ \beta I_1& \beta S_1-\left(\mu +\delta +\gamma \right)\end{array}\right]$

我们得到平衡点 $P_1$ 的特征方程为

$\left(\lambda +\beta I_1+\mu +\epsilon \right)\left(\lambda -\beta S_1+\mu +\delta +\gamma \right)-\left(-\beta I_1\right)\left(\beta S_1-\gamma +\epsilon \right)=0$

令特征方程的两个特征值分别为 ${\lambda }_1,{\lambda }_2$，我们计算可得

$\begin{array}{l}{\lambda }_1{\lambda }_2=\beta I_1\left(\mu +\delta \right)+\epsilon \beta I_1\\ {\lambda }_1+{\lambda }_2=-\beta I_1-\mu -\epsilon \end{array}$

当 $R_0>1$ 时，满足 ${\lambda }_1{\lambda }_2>0,{\lambda }_1+{\lambda }_2<0$，这意味着此时该特征方程的两个负特征值。所以当 $R_0>1$ 时，地方病平衡点 $P_1$ 是局部渐近稳定的。

3.2. 系统S_G2的局部渐近稳定性

定理4 对于 $S_{G2}$ 系统，当 $R_c<1$ 时， ${P^{\prime }}_0$ 是局部渐近稳定的，当 $R_c>1$， $P_2$ 是局部渐近稳定的。

证明：由于 ${P^{\prime }}_0$ 和 $P_0$ 是重合的，故系统 $S_{G2}$ 在 ${P^{\prime }}_0$ 处的局部稳定性证明与系统 $S_{G1}$ 在 $P_0$ 处的局部稳定性证明相同。从而我们得出当 $R_c<1$ 时， ${P^{\prime }}_0$ 是局部渐近稳定的。当 $R_c>1$ 时， ${P^{\prime }}_0$ 是不稳定的。

我们令系统 $S_{G2}$ 在 $P_2$ 处特征方程的特征值为 ${\lambda }_1,{\lambda }_2$，则只有 ${\lambda }_1{\lambda }_2>0,{\lambda }_1+{\lambda }_2<0$ 时，在 $P_2$ 处特征方程的特征值皆为负，此时 $P_2$ 才是局部渐近稳定的。

为证明 ${\lambda }_1{\lambda }_2>0,{\lambda }_1+{\lambda }_2<0$，我们令 $l=\frac{m\left(\mu +\epsilon \right)\left(\mu +\delta +\gamma \right)}{\beta \left(\mu +\delta +\epsilon \right)}{\text{e}}^{-m{I}_c+\frac{m\left(\mu +\epsilon \right)}{\mu +\delta +\epsilon }}$

此时有 $S_2=\frac{\mu +\delta +\epsilon }{m\left(\mu +\epsilon \right)}W\left(l\right)$， $I_2=\frac{\mu +\epsilon }{\mu +\delta +\epsilon }-\frac{1}{m}W(\; l\; )$

由Lambert W函数 [12] [15] [16] 可得

$W\left(l\right){\text{e}}^{W\left(l\right)}=l=\frac{m\left(\mu +\epsilon \right)\left(\mu +\delta +\gamma \right)}{\beta \left(\mu +\delta +\epsilon \right)}{\text{e}}^{-m{I}_c+\frac{m\left(\mu +\epsilon \right)}{\mu +\delta +\epsilon }}$, $W\left(l\right)=\frac{m\left(\mu +\epsilon \right)\left(\mu +\delta +\gamma \right)}{\beta \left(\mu +\delta +\epsilon \right)}{\text{e}}^{-m{I}_c+\frac{m\left(\mu +\epsilon \right)}{\mu +\delta +\epsilon }}{\text{e}}^{-W(\; l\; )}$

所以有

$\begin{array}{c}{\lambda }_1+{\lambda }_2=\beta {\text{e}}^{-m\left(I_2-I_c\right)}{S}_2-m\beta {\text{e}}^{-m\left(I_2-I_c\right)}{I}_2-\left(2\mu +\delta +\gamma +\epsilon \right)\\ =-{\text{e}}^{-m\left(I_2-I_c\right)}\left(-\beta S_2+m\beta I_2+\left(2\mu +\delta +\gamma +\epsilon \right)e^{m\left(I_2-I_c\right)}\right)\\ =-{\text{e}}^{-m\left(I_2-I_c\right)}\left(-\frac{\beta \left(\mu +\delta +\epsilon \right)}{m\left(\mu +\epsilon \right)}W\left(l\right)+m\beta I_2+\left(2\mu +\delta +\gamma +\epsilon \right)e^{\frac{m\left(\mu +\epsilon \right)}{\mu +\delta +\epsilon }-m{I}_c}{e}^{-W\left(l\right)}\right)\\ =-{\text{e}}^{-m\left(I_2-I_c\right)}\left(-\frac{\beta \left(\mu +\delta +\gamma \right)\left(\mu +\delta +\epsilon \right)}{m\left(\mu +\epsilon \right)\left(\mu +\delta +\gamma \right)}W\left(l\right)+m\beta I_2+\frac{\beta \left(2\mu +\delta +\gamma +\epsilon \right)\left(\mu +\delta +\epsilon \right)}{m\left(\mu +\epsilon \right)\left(\mu +\delta +\gamma \right)}W\left(l\right)\right)\\ =-{\text{e}}^{-m\left(I_2-I_c\right)}\left(m\beta I_2+\frac{\beta W\left(l\right)\left(\mu +\delta +\epsilon \right)}{m\left(\mu +\delta +\gamma \right)}\right)<0\end{array}$

下面证明 ${\lambda }_1{\lambda }_2>0$，首先易得

${\text{e}}^{m\left(I_2-I_c\right)}={\text{e}}^{-m{I}_c+\frac{m\left(\mu +\epsilon \right)}{\mu +\delta +\epsilon }}{\text{e}}^{-W\left(l\right)}=\frac{\beta \left(\mu +\delta +\epsilon \right)}{m\left(\mu +\epsilon \right)\left(\mu +\delta +\gamma \right)}W(\; l\; )$

所以

$\begin{array}{c}{\lambda }_1{\lambda }_2=\beta {\text{e}}^{-m\left(I_2-I_c\right)}{I}_2\left(\mu +\delta +\epsilon \right)+\left(\mu +\epsilon \right)\left(\mu +\delta +\gamma \right)+\left(\mu +\epsilon \right)\beta {\text{e}}^{-m\left(I_2-I_c\right)}{S}_{2}m{I}_2-\left(\mu +\epsilon \right)\beta {\text{e}}^{-m\left(I_2-I_c\right)}{S}_2\\ ={\text{e}}^{-m\left(I_2-I_c\right)}\beta \left(\mu +\delta +\epsilon \right)\left(I_2+\frac{\left(\mu +\epsilon \right)\left(\mu +\delta +\gamma \right)}{\beta \left(\mu +\delta +\epsilon \right)}{\text{e}}^{m\left(I_2-I_c\right)}+\frac{m\left(\mu +\epsilon \right)}{\mu +\delta +\epsilon }{S}_2{I}_2-\frac{\mu +\epsilon }{\mu +\delta +\epsilon }{S}_2\right)\\ ={\text{e}}^{-m\left(I_2-I_c\right)}\beta \left(\mu +\delta +\epsilon \right)\left(I_2+\frac{m\left(\mu +\epsilon \right)S_2{I}_2}{\mu +\delta +\epsilon }+\frac{1}{m}W\left(l\right)-\frac{1}{m}W\left(l\right)\right)\\ ={\text{e}}^{-m\left(I_2-I_c\right)}\beta \left(\mu +\delta +\epsilon \right)\left(I_2+\frac{m\left(\mu +\epsilon \right)S_2{I}_2}{\mu +\delta +\epsilon }\right)>0\end{array}$

当 $I_2>0$ 时，都 ${\lambda }_1{\lambda }_2>0,{\lambda }_1+{\lambda }_2<0$ 成立。即 $R_c>1$ 时，该特征方程有两个负特征值，这表明当 $R_c>1$ 时， $P_2$ 是局部渐近稳定的。

4. 全局渐近稳定性

为得到各个平衡点的全局渐近稳定性，首先判断系统是否存在极限环。

定理5 系统(4)不存在极限环。

证明 运用Bendixson-Dulac判别法 [15] [17] 验证系统(4)不存在极限环，首先我们令 $f=\mu -\beta f\left(I\right)SI-\mu S+\gamma I+\epsilon \left(1-S-I\right)$， $g=\beta f\left(I\right)SI-\left(\mu +\delta +\gamma \right)I$ 并考虑如下连续的Dulac函数： $D\left(S,I\right)=1/\left(SI\right)$。

当 $0<I\le I_c$ 时， $\frac{\partial \left(Df\right)}{\partial S}+\frac{\partial \left(Dg\right)}{\partial I}=-\frac{\mu +\gamma I+\epsilon \left(1-I\right)}{S^{2}I}<0$

当 $I>I_c$ 时， $\frac{\partial \left(Df\right)}{\partial S}+\frac{\partial \left(Dg\right)}{\partial I}=-\frac{\mu +\gamma I+\epsilon \left(1-I\right)}{S^{2}I}-m\beta {\text{e}}^{-m\left(I-I_c\right)}<0$

所以系统(4)不存在极限环。

由于采用(1)作为媒体影响函数的模型(2)实际为一个分段光滑系统，我们排除了极限环的存在性，并借助 [12] 提出的真假平衡态方法，进一步讨论各个平衡点的全局稳定性。

1) 对于系统 $S_{G1}$，显然平衡点 $P_0$ 位于区域 $G_1$ 中，因此 $P_0$ 是真平衡态。若地方病平衡点 $P_1$ 是真平衡态，应有 $I_1\le I_c$，即：

$R_0\le \frac{\mu +\epsilon }{\mu +\epsilon -\left(\mu +\delta +\epsilon \right)I_c}$

因此，如果满足条件 $R_0\le \frac{\mu +\epsilon }{\mu +\epsilon -\left(\mu +\delta +\epsilon \right)I_c}$，地方病平衡点 $P_1$ 位于区域 $G_1$ 内， $P_1$ 为真平衡态，否则为假平衡态。

2) 对于系统 $S_{G2}$，当且仅当 $R_c>1$ 时， $P_2$ 有意义。此时 ${P^{\prime }}_0$ 在区域 $G_1$ 中，因此是假平衡态。若 $I_2>I_c$ 时，地方病平衡点 $P_2$ 是真平衡态。即当 $R_0>\frac{\mu +\epsilon }{\mu +\epsilon -\left(\mu +\delta +\epsilon \right)I_c}$ 时，地方病平衡点 $P_2$ 是真平衡态，否则为假平衡态。

由此可得出以下定理：

定理6 当 $R_0<1$ 时，无病平衡点 $P_0\left({P^{\prime }}_0\right)$ 是全局渐近稳定的。

证明：当 $R_0<1$ 时， $P_0$ 是存在的且是局部渐近稳定的， $P_0$ 是真平衡态。下面分两种情况来讨论平衡点的全局稳定性。

当 $R_0<{\text{e}}^{-m{I}_c}$ 时，得到 $R_0<1$，则地方病平衡点 $P_2$ 不存在。系统 $S_{G2}$ 的假平衡态 ${P^{\prime }}_0$ 存在，局部渐近稳定且在 $G_1$ 中。因此所有起点在 $G_2$ 中的曲线最终都会趋于 $G_1$ 中的点 ${P^{\prime }}_0$。所以 $G_2$ 中的曲线最终将会进入 $G_1$。而 $P_0$ 是 $G_1$ 中的局部渐近稳定点，故所有 $G_1$ 中的曲线都会趋于 $P_0$。又因系统(4)不存在极限环。因此无论曲线的起点是在 $G_1$ 还是 $G_2$，它们都将趋于无病平衡点 $P_0$。

当 ${\text{e}}^{-m{I}_c}<R_0<1$ 时，得到 $R_c>1$。因此系统 $S_{G2}$ 的平衡点 $P_2$ 存在且是局部渐近稳定的。故所有从 $G_2$ 开始的曲线将会趋于 $P_2$。但由于 $R_0<1$ 可得地方病平衡点 $P_2$ 在区域 $G_1$ 中，为假平衡态。故所有从 $G_2$ 开始的曲线都将进入 $G_1$。又因 $R_0<1$，所有 $G_1$ 中的曲线都将趋于 $P_0$。总之，在此条件下所有从 $G_1$ 和 $G_2$ 出发的曲线都将趋于无病平衡点 $P_0$。

因此得出结论，当 $R_0<1$ 时，系统(4)中所有的解都将趋于无病平衡点 $P_0$。因为 $P_0$ 和 ${P^{\prime }}_0$ 是重合的。因此无病平衡点 $P_0\left({P^{\prime }}_0\right)$ 是全局渐近稳定的。

定理7 当 $1<R_0<\frac{\mu +\epsilon }{\mu +\epsilon -\left(\mu +\delta +\epsilon \right)I_c}$ 时，地方病平衡点P₁全局渐近稳定。当 $R_0>\frac{\mu +\epsilon }{\mu +\epsilon -\left(\mu +\delta +\epsilon \right)I_c}$ 时，地方病平衡点 $P_2$ 全局渐近稳定。

证明：当 $1<R_0<\frac{\mu +\epsilon }{\mu +\epsilon -\left(\mu +\delta +\epsilon \right)I_c}$ 时，由 $R_0>1$，可知此时 $P_0$ 和 ${P^{\prime }}_0$ 不稳定。通过计算得 $R_c>1$。因此系统 $S_{G2}$ 的平衡点 $P_2$ 存在且是局部渐近稳定的。但由 $R_0<\frac{\mu +\epsilon }{\mu +\epsilon -\left(\mu +\delta +\epsilon \right)I_c}$ 可得地方病平衡点 $P_2$ 在区域 $G_1$ 中，故为假平衡态。而 $P_1$ 存在且是局部渐近稳定的，此条件下 $P_1$ 在 $G_1$ 中， $P_1$ 是真平衡态。由此，所有起点在区域 $G_2$ 中的曲线最终都将会进入区域 $G_1$。而所有在 $G_1$ 中的曲线将会最终趋于 $P_1$。因此，当 $1<R_0<\frac{\mu +\epsilon }{\mu +\epsilon -\left(\mu +\delta +\epsilon \right)I_c}$ 时，地方病平衡点 $P_1$ 是全局渐近稳定的。

当 $R_0>\frac{\mu +\epsilon }{\mu +\epsilon -\left(\mu +\delta +\epsilon \right)I_c}$ 时，可得 $R_c>1$。此时 $P_0$ 和 ${P^{\prime }}_0$ 不稳定，而 $P_1$ 和 $P_2$ 存在且局部渐近稳定， $P_1$ 和 $P_2$ 都在区域 $G_2$ 上。所以 $P_1$ 是假平衡态。所有从 $G_1$ 出发的曲线都会进入区域 $G_2$ 中。同时，由于真平衡态 $P_2$ 在区域 $G_2$ 中是局部渐近稳定的。所有 $G_2$ 中的曲线都将趋于 $P_2$。综上，从 $G_1$ 或 $G_2$ 出发的任意曲线都将趋于 $P_2$，即真平衡态 $P_2$ 在 $R_0>\frac{\mu +\epsilon }{\mu +\epsilon -\left(\mu +\delta +\epsilon \right)I_c}$ 时是全局渐近稳定的。

5. 数值模拟

由定理7，当 $1<R_0<\frac{\mu +\epsilon }{\mu +\epsilon -\left(\mu +\delta +\epsilon \right)I_c}$ 时，地方病平衡点 $P_1$ 是全局渐近稳定的。当 $R_0>\frac{\mu +\epsilon }{\mu +\epsilon -\left(\mu +\delta +\epsilon \right)I_c}$ 时，地方病平衡点 $P_2$ 是全局渐近稳定的。下面我们在图1的两个区域 $G_1,G_2$ 中选取初值分别为[0.1, 0.9]，[0.2, 0.4]，[0.1, 0.63]，[0.3, 0.1]，[0.15, 0.22]的五个初值，曲线最终都会趋于平衡点 $P_1$，反映了 $P_1$ 的全局稳定性。图1中的参数为 $\mu =0.3$， $\delta =0.2$， $\beta =0.8$， $\gamma =0.1$， $\epsilon =0.3$， $ic=0.3$， $m=0.8$，故有 $R_0\approx 1.33$， $\frac{\mu +\epsilon }{\mu +\epsilon -\left(\mu +\delta +\epsilon \right)I_c}\approx 1.67$， $1<R_0<\frac{\mu +\epsilon }{\mu +\epsilon -\left(\mu +\delta +\epsilon \right)I_c}$。并在图2中选取了初值为[0.2, 0.4, 0.4]，用与图1相同参数模拟出 $S,I,Q$ 的人口比例随时间的变化， $S,I,Q$ 最终会趋于平衡。

同样，在图3两个区域 $G_1,G_2$ 中分别选取初值为[0.1, 0.9]，[0.2, 0.4]，[0.1, 0.63]，[0.3, 0.1]，[0.15, 0.22]的五个初值点，曲线最终都会趋于平衡点 $P_2$，反映了 $P_2$ 的全局稳定性。图3中的参数为 $\mu =0.2$， $\delta =0.1$，

$\beta =0.7$， $\gamma =0.05$， $\epsilon =0.25$， $ic=0.2$， $m=0.8$，故有 $R_0=2$， $\frac{\mu +\epsilon }{\mu +\epsilon -\left(\mu +\delta +\epsilon \right)I_c}\approx 1.32$， $R_0>\frac{\mu +\epsilon }{\mu +\epsilon -\left(\mu +\delta +\epsilon \right)I_c}$。在图4中选取了初值为[0.3, 0.1, 0.6]，用与图3相同参数模拟出 $S,I,Q$ 的人口

比例随时间的变化， $S,I,Q$ 最终都会趋于稳定。

隔离率 $\delta$ 也会影响疾病传播，我们在模型(3)中选取初值为 $S=0.8$， $I=0.1$，并选取不同的隔离率 $\delta$，分别为 $\delta =0.1$， $\delta =0.15$， $\delta =0.2$，令参数 $\mu =0.2$， $\beta =0.7$， $\gamma =0.05$， $\epsilon =0.25$， $ic=0.2$， $m=0.5$，进行数值模拟，当 $\delta$ 越大感染者比例越少，反映隔离策略可以有效抑制疾病传播。

临界值 $I_c$ 和影响因子m也会影响疾病传播，我们在图6和图7中选取与图5相同参数，并分别选取不同的 $I_c$ 值和m值进行数值模拟，当 $I_c$ 越小，感染者比例越少；当m值越大，感染者比例越少。反映临界值 $I_c$ 和影响因子m也会抑制疾病传播。图6中选取初值为 $S=0.8$， $I=0.1$，参数为 $\mu =0.2$， $\beta =0.7$， $\gamma =0.05$， $\epsilon =0.25$， $\delta =0.1$， $m=0.5$。图7中选取初值为 $S=0.8$， $I=0.1$，参数为 $\mu =0.2$， $\beta =0.7$， $\gamma =0.05$， $\epsilon =0.25$， $\delta =0.1$， $ic=0.2$。

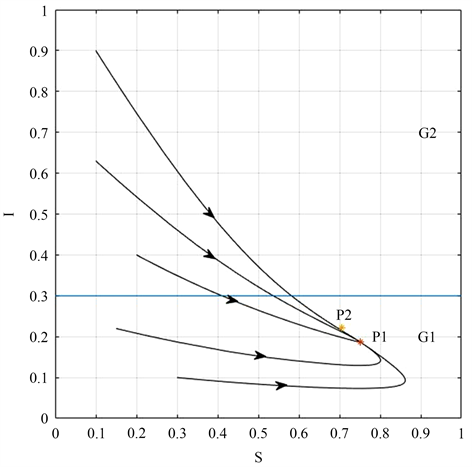
Figure 1. Global stability of P₁ in G₁

图1. G₁中P₁的全局稳定性

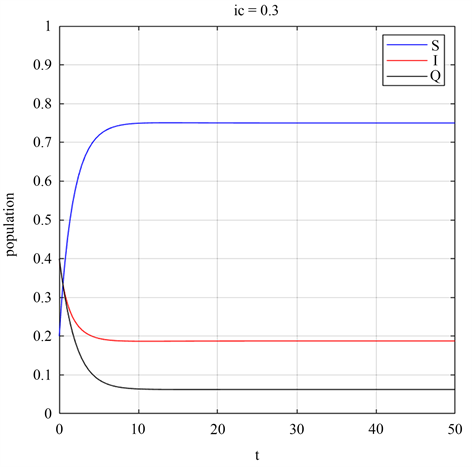
Figure 2. The proportion of the population in S, I, Q changes over time

图2. S, I, Q的人口比例随时间变化

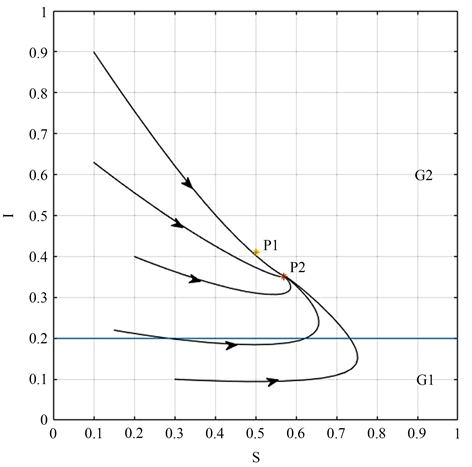
Figure 3. Global stability of P₂ in G₂

图3. G₂中P₂的全局稳定性

Figure 4. The proportion of the population in S, I, Q changes over time

图4. S, I, Q的人口比例随时间变化

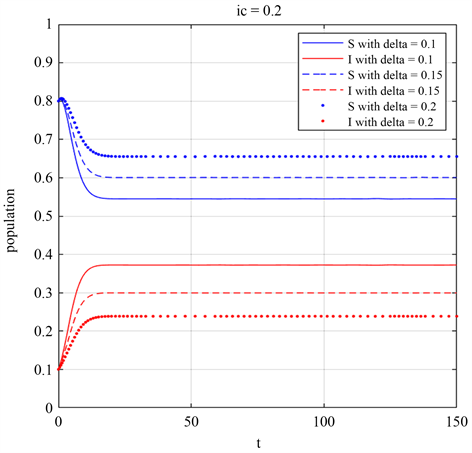
Figure 5. The δ value increases, and the proportion of infective individuals decreases

图5. δ值变大，感染者比例变小

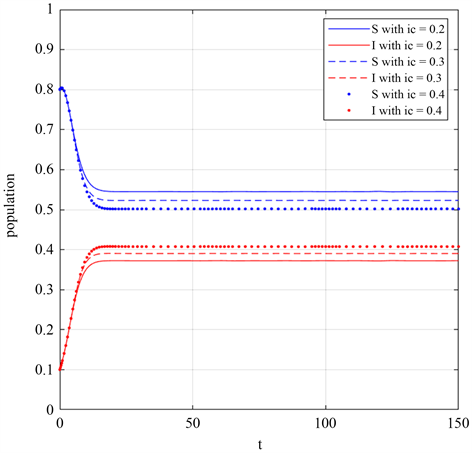
Figure 6. The I_c value decreases, and the proportion of proportion of infective individuals decreases

图6. I_c值变小，感染者比例变小

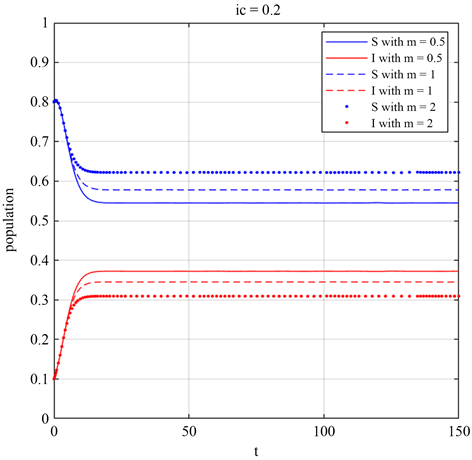
Figure 7. The m value increases, and the infective individuals decreases

图7. m值变大，感染者比例变小

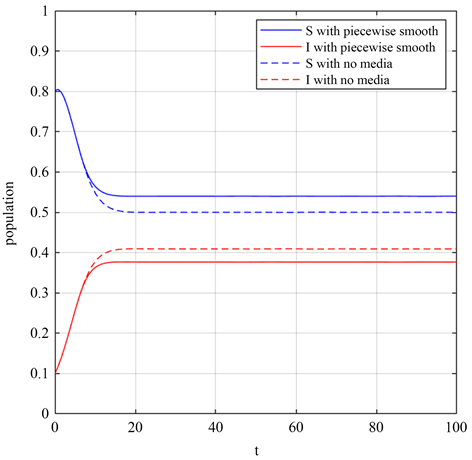
Figure 8. Comparison of population proportions over time for piecewise smooth media, no media impact functions

图8. 分段光滑媒体、无媒体影响函数的人口比例随时间变化对比图

我们在SIQS模型中分别引入分段光滑媒体影响函数，无媒体影响函数进行数值模拟(图8所示)，通过对比发现采用分段光滑媒体影响函数的感染人数更少，更具有现实意义。图8参数为 $\mu =0.2$， $\beta =0.7$， $\gamma =0.05$， $\epsilon =0.25$， $\delta =0.1$， $m=1$， $ic=0.3$。

6. 结论

本文采用分段光滑函数作为媒体报道函数引入到SIQS模型中。首先，分析模型的平衡点，通过计算基本再生数 $R_0$ 和阈值参数 $R_c$，给出定理1和定理2。运用线性化方法对平衡点的局部稳定性进行分析，给出定理3和定理4。通过Bendixson-Dulac判别法排除极限环的存在性，得到定理5。并运用真假平衡态分析了系统(4)的全局稳定性，得到定理6和定理7。最后，通过数值模拟，反映了媒体报道和隔离策略对疾病传播的影响。未来我们还将在传染病模型中引入不同的分段光滑媒体影响函数进行研究，为媒体报道的传染病模型提供一个更现实、更自然的描述。

基金项目

国家自然科学基金项目(批准号11901052)。