基于小波变换的压缩全变分图像降噪模型

Wavelet-Based Compressive Total Variation Model for Image Denoising

摘要: 从被噪声污染的图像(即观测图像)中恢复原始图像是图像处理的主要任务之一，原始图像矩阵在小波变换域其近似系数矩阵是低秩的，并且对应的梯度变换矩阵是低秩且稀疏的，基于此先验知识，对观测图像的近似系数矩阵使用压缩全变分降噪模型即通过极小化一个含有保真项和正则化项的能量泛函实现降噪，利用小波逆变换重构图像，可实现观测图像降噪。

Abstract: It is one of the main tasks of image processing to recover the original image from the noise-polluted image (observed image). The approximate coefficient matrix of the original image matrix in the wavelet transform domain is low-rank, and the corresponding gradient transform matrix is low-rank and sparse. Based on this prior knowledge, the compressed total variation image denoising model is used for the approximate coefficient matrix of the observed image, that is, the denoising of the observed image is realized by minimising an energy functional containing the fitting term and regularization term, and the image is reconstructed by using the inverse wavelet transform.

1. 引言

当今，针对图像处理的应用已涉及众多领域，特别是图像识别和人工智能等方面，图像处理都是重要的组成环节和重要基础。在图像在采集、传输、接收的过程中往往会不可避免地受到干扰，使得最终获取的图像中含有大量噪声，这些噪声降低了图像的质量，因此从含有模糊和噪声的退化图像中复原原始图像有着重要的实用研究价值。在图像去噪处理中，需要考虑的主要因素是在去除噪声的同时，必须确保图像自己具有特征的完整性，这些特征主要包括：图像边缘轮廓信息、图像纹理信息和图像色彩等 [1]。记 $u\in R^{m\times n}$ 为原始图像，观测的低质量图像 $b\in R^{m\times n}$ 本模板由 受模糊和噪声的干扰而形成。在数学上，图像复原一般可表示为以下问题的逆问题：

$b=Au+\eta$ (1)

其中 $\eta$ 为噪声，A为线性算子。由于A往往是病态的，无法直接求逆或者会导致不好的结果。正则化是求解不适定问题的常见方法，可以提高解的质量，其主要想法是加入正则化项 $R\left(u\right)$，加入正则项后此逆问题的一般模型可表示为：

$\hat{u}=\arg {\min }_{u\in R^{m\times n}}\left\{J\left(u\right)+\rho \varphi \left(u\right)\right\}$ (2)

$\varphi \left(u\right)$ 是数据拟合项，一般选为 $\varphi \left(u\right)=\frac{{\Vert Au-b\Vert }^2}{2}$， $\rho >0$ 为平衡参数， $J\left(u\right)$ 为正则项， $\hat{u}$ 为模型的最

优解。 $J\left(u\right)$ 的选取需要考虑图像所具有的先验信息，选择不同的 $J\left(u\right)$ 会产生不同的降噪模型。本文以压缩全变分图像降噪模型为主要参考，提出了一种新的降噪算法，文章结构如下：第二部分介绍当前比较常用的效果较好的正则化模型及相关符号的含义，第三部分将详细地介绍本算法，第四部分展示各模型图像恢复的模拟结果，第五部分为文章的总结。

2. 符号与其他算法

观察到受噪声污染的图像具有较大的全变分，Rudin提出了经典的全变分正则化模型(Total Variation, TV) [1]

$\text{TV}\left(u\right)={〚\nabla u〛}_1$ (3)

其中 $\nabla$ 为梯度算子，设 $D_{x}u,D_{y}u\in R^{m\times n}$ 分别为图像的水平和垂直方向的导数算子，则 $D=\left[D_{x}u,D_{y}u\right]=\nabla$，恢复的图像具有分段常数强度，保留了尖锐的边缘，不足之处是恢复的图像可以观察到阶梯效应，图像呈现出油画风格。

广义全变分正则化模型(Total Generalized, TGV) [2] 考虑了高阶导数，不同的区域使用不同的正则方式，以二阶离散TGV为例，设 $V=C_c^2\left(\Omega ,R^2\right)$ 为紧支撑张量场，模型如下 [3] [4]：

${\text{TGV}}_{\alpha }^2\left(u\right)={\min }_{v\in V}\left\{{\alpha }_1{\Vert Du-v\Vert }_1+{\alpha }_0{\Vert \epsilon \left(v\right)\Vert }_1\right\}$ (4)

其中 $\epsilon \left(v\right)=\frac{Du+D^{\text{T}}u}{2}$， $\alpha =\left({\alpha }_0,{\alpha }_1\right)$，若图像区域 $\Omega ={\Omega }_1\cup {\Omega }_2$， ${\Omega }_1\cup {\Omega }_2=\varnothing$，其中 ${\Omega }_1,{\Omega }_2$ 分别表示图像

的光滑区域和边缘附近区域，由于在光滑区域，图像的 $D^{2}u$ 较小，在边缘附近，图像的 $Du$ 相对于 $D^{2}u$ 更小 [5]，从而选取

$v=\{\begin{array}{l}Du,u\in {\Omega }_1\\ 0,u\in {\Omega }_2\end{array}$ (5)

则模型可写为：

${\text{TGV}}_{\alpha }^2\left(u\right)=\{\begin{array}{l}{\alpha }_0{\Vert D^{2}u\Vert }_1,u\in {\Omega }_1\\ {\alpha }_1{\Vert Du\Vert }_1,u\in {\Omega }_2\end{array}$ (6)

该模型考虑了二阶导数，不仅刻画了分段光滑函数在结点处函数值的跳跃情况，而且刻画了一阶导数的跳跃情况，恢复的图像具有分段多项式强度，对光滑区域刻画得更精确，在图像的细节和边缘恢复效果更好，有效避免了阶梯效应。

核范数可以有效地刻画矩阵的秩，将TGV模型中的 $l_1$ 范数替换为核范数，可得到核范数下的广义全变分正则化模型(Nuclearnorm Total Variation, NTGV)，可以刻画图像的低秩特征：

${\text{NTGV}}_{\alpha }^2\left(u\right)=\{\begin{array}{l}{\alpha }_0{\Vert D^{2}u\Vert }_{\ast },u\in {\Omega }_1\\ {\alpha }_1{\Vert Du\Vert }_{\ast },u\in {\Omega }_2\end{array}$ (7)

基于图像具有稀疏性，其梯度是低秩且稀疏的先验知识，以及压缩感知理论指出：信号稀疏程度越大，重构的信号的准确度就会越高。李朋提出压缩全变分正则化模型(Compressive total variation, CTV) [6]，在文献 [5] 中通过对图像进行满秩分解，观察得到的分解矩阵，可知原矩阵具有低秩性，证明了以下结论成立：

$\text{rank}\left(D_{x}u\right)\approx \text{rank}\left(u\right)\approx \text{rank}\left(D_{y}u\right)$ (8)

即梯度变换几乎不改变矩阵的秩，图像的梯度矩阵也具有低秩的特点。综合以上先验知识，将图像复原问题可以描述为求解 使得

$b=Au+\eta$

${\Vert \left[\begin{array}{c}{D}_{x}u\\ D_{y}u\end{array}\right]\Vert }_0<2mn$

$\text{rank}\left(\left[\begin{array}{cc}{D}_{x}u& 0\\ 0& D_{y}u\end{array}\right]\right)<\min \left\{2m,2n\right\}$

$\text{rank}\left(u\right)<\min \left\{2m,2n\right\}$ (9)

选取正则项为

$J\left(u\right)=\lambda TV\left(u\right)+\tau {\Vert u\Vert }_{\ast }+{\text{NTGV}}_{\alpha }^2\left(u\right)=\lambda {\Vert Du\Vert }_1+\tau {\Vert u\Vert }_{\ast }+{\min }_{v\in V}\left\{{\alpha }_1{\Vert Du-v\Vert }_{\ast }+{\alpha }_0{\Vert \epsilon \left(v\right)\Vert }_{\ast }\right\}$ (10)

拟合项为 $\varphi \left(u\right)=\frac{{\Vert Au-b\Vert }^2}{2}$，建立的基于CTV的图像降噪模型如下：

${\min }_{v,u}\left\{\lambda {\Vert Du\Vert }_1+\tau {\Vert u\Vert }_{\ast }+{\alpha }_1{\Vert Du-v\Vert }_{\ast }+{\alpha }_0{\Vert \epsilon \left(v\right)\Vert }_{\ast }+\frac{\rho }{2}{\Vert Au-b\Vert }_2^2\right\}$ (11)

其中 $\rho ,\tau >0$ 为平衡参数，可转化为线性约束可分凸优化问题，利用惯性近端交替方向乘子法(ADMM) [7] 进行求解，该模型继承了NTGV的优势，又刻画了图像低秩和其梯度的低秩且稀疏的特性，在图像去噪方面效果明显。

3. 基于小波变换的压缩全变分图像降噪模型

小波变换(Wavelet Transform)的基本思想和传统的傅里叶变换是一致的，它也是用一族函数来表示信号或函数，这一族函数称之为小波函数系，小波函数系是由一基本小波函数平移和伸缩构成的，小波变换是一种窗口面积恒定，窗口形状可变(时域窗口和频域窗口均可变)的时–频局域化分析方法 [8]，具有良好的时频特性、多分辨率分析特性、稀疏表示特性和精准可逆性，广泛应用于计算机视觉领域 [9]，在图像处理中有非常重要的应用，包括图像压缩、图像去噪、图像融合、图像分解和图像增强等图像处理的几乎所有阶段。利用小波分析处理信号的过程一般为：信号经过小波变换后分解为低频分量和高频分量，低频部分具有光滑的表面和纹理信息，而高频部分则捕捉更复杂的纹理细节 [10] [11]，对高频分量和低频分量分别经过处理后利用小波逆变换进行重构。设 $\psi \left(t\right)\in L^{2}R$ ( $L^{2}R$ 表示平方可积的实数空间，即能量有限的信号空间)，离散小波基为：

${\psi }_{j,k}\left(t\right)=a^{-\frac{j}{z}}\psi \left(a^{-j}t-k\right),j,k\in Z$ (12)

其中a为散化伸缩因子，k为离散化平移因子，j为频域，小波系数代表了小波与局部信号之间的相关程度。对图像进行非下采样的离散小波变换(Nonsampling Discrete Wavelet Transform, NDWT)后，信号被分为四个不同波段，分别是低通LL^T，水平LH^T，垂直HL^T和对角细节HHL^T波段。分别对应四个矩阵：近似系数矩阵 $A_{m\times n}$，水平系数矩阵 $H_{m\times n}$，垂直系数矩阵 $V_{m\times n}$，对角系数矩阵 $D_{m\times n}$。经过对几组图片进行测试，计算上述四个矩阵的秩、梯度矩阵的秩和稀疏指标，得到近似系数矩阵 $A_{m\times n}$ 具有低秩的特点，并且 $A_{m\times n}$ 的梯度具有低秩性和稀疏性。基于以上的先验知识，提出基于小波变换的压缩全变分图像降噪模型(Wavelet-based Compressive Total Variation for Image Denoising, WCTV)：对加入噪声的图像进行非采样的离散小波变换，对其近似系数矩阵 $A_{m\times n}$ 使用基于$CTV$的图像降噪模型进行降噪处理，结果记为 $A{\left(\text{CTV}\right)}_{m\times n}$，对 $A{\left(\text{CTV}\right)}_{m\times n}$， $H_{m\times n}$， $V_{m\times n}$， $D_{m\times n}$ 进行下采样后使用离散小波逆变换(Inverse Discrete Wavelet Transform, IDWT)，对图像进行重构，可求解原逆问题(1)，具体算法流程示意图见图1。

为了验证文中提出的模型的降噪效果和可靠性，本文使用Matlab2020a软件对图像进行仿真实验，测试图片为Lena，Shape，Dartboard，Text，Peppers，加入高斯白噪声来模拟受噪声污染的图像，其中高斯白噪声的幅度分布服从高斯分布，功率谱密度服从均匀分布。以信噪比(Signal to Noise Ratio, SNR)和峰值信噪比(Peak Signal to Noise Ratio, PSNR)作为恢复图像质量的评判标准，SNR代表目标信号与噪声信号的能量比值，PSNR表示信号最大可能功率和影响它的表示精度的破坏性噪声功率的比值，值越大代表失真图像与参考图像越接近，即图像复原效果越好。计算公式为：

$\text{SNR}=10\times {\log }_{10}\frac{{\displaystyle {\sum }_{x=1}^n{\displaystyle {\sum }_{y=1}^{m}u{\left(x,y\right)}^2}}}{\text{MSE}}$

$\text{PSNR}=10{\text{log}}_{10}\frac{{255}^2}{\text{MSE}}$

其中MSE为真值与噪声图像的均方误差。将本文提出的WCTV降噪模型与基于TV，TGV，CTV的降噪模型型进行对比，图2展示了通过Matlab仿真的效果，包括输入的真值、加入噪声的输入图像、使用各模型恢复的图像，视觉上可见使用WCTV模型恢复的图像效果优于以上其它模型：噪声效果出现显著的减小，图像的细节保存较好，整体更为均匀，没有出现较为显著的噪声色板，局部纹理较为清晰，轮廓也非常完整，具有较高的实际应用性。表1与表2显示了对几个经典图像分别使用以上模型降噪的SNR、PSNR值，相比于其他模型，WCTV表现出明显的优势。

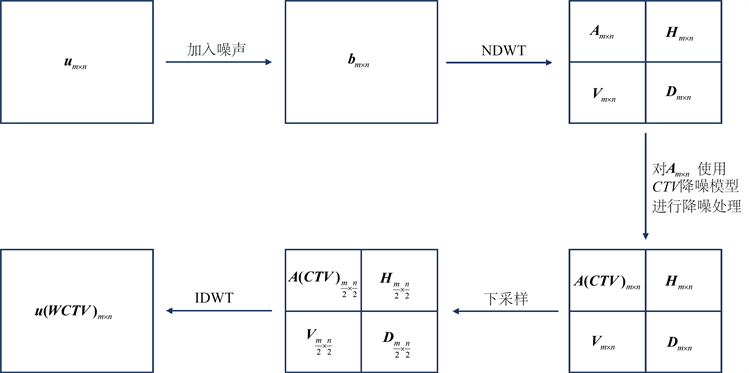
Figure 1. The flow chart of the WCTV algorithm

图1. WCTV算法流程示意图

Figure 2. Test results of each model

图2. 各模型测试结果

Table 1. SNR

表1. 图像信噪比

Table 2. PSNR

表2. 图像峰值信噪比

4. 总结

本文考虑图像经过小波变换后近似系数矩阵具有稀疏性，其梯度矩阵具有低秩且稀疏的特点，在基于CTV的图像降噪模型对具有以上先验知识的图像恢复效果较好的基础上，提出了基于小波变换的压缩全变分图像降噪模型：对加入噪声的图像进行非采样的离散小波变换，对其近似系数矩阵 $A_{m\times n}$ 使用基于CTV的图像降噪模型进行降噪处理，结果记为 $A{\left(\text{CTV}\right)}_{m\times n}$，对 $A{\left(\text{CTV}\right)}_{m\times n}$， $H_{m\times n}$， $V_{m\times n}$， $D_{m\times n}$ 进行下采样后使用离散小波逆变换重构，进而实现原图像降噪。在数值实验方面，我们测试了具有代表性的图片，对比了信噪比等指标，实验结果证明本模型可以有效去除噪声，保留细节，画质均匀，效果明显优于其他降噪模型。在未来的工作中，一方面本文选取Haar小波作为稀疏基，未来考虑其他类型稀疏基；另一方面考虑本模型在图像去模糊等方向的应用。