1. 引言
全波形反演(Full waveform inversion,简称为FWI)是一种能有效地利用地震波场运动学和动力学信息的反演方法,具有高分辨率的成像特性。理论上,求解FWI问题可以转化为求解如下偏微分方程约束的极小化问题 [1] [2]
(1)
其中,
表示
范数,m是反演参数(如速度,密度等),R代表线性投影算子,它用于提取接收器位置的波场,
表示观测数据,合成波场u满足方程
(2)
方程(2)可以是频率域或时间域声波方程、弹性波方程等。从数值计算角度,本文只考虑2D频率域声波方程,且假设声波方程中密度恒定,模型参数为压力波速度
,因此,方程(2)即为著名的Helmholtz方程
(3)
其中,
是角频率,
是声波速度,
是震源项。
FWI通常是一个不适定问题,需要引入适当的正则化方法才能获得较好的反演结果。目标函数(1)引入正则化惩罚项变为
(4)
其中,
是惩罚项(正则化项),其具有添加先验信息以限制模型空间的作用以及稳定极小化过程的作用,
为正则化参数,其作用是平衡正则化项和数据拟合项,取值取决于具体的问题。常见的正则化方法有基于
-norm的正则化,如Tikhonov正则化 [3] [4],该方法具有获取过度光滑的解的作用;基于
-norm的正则化,如全变差(TV)正则化 [5] [6] [7],其可以很好地保留解的边缘信息。
TV正则化具有保留重构解的不连续性信息的优点。针对FWI反演问题,地层介质模型参数(声波速度)往往具有不连续性且在幅度上通常存在较大差异。因此,基于TV正则化的反演方法广泛应用于求解FWI反演问题 [8] [9] [10]。然而,从全变差函数的定义可知,TV正则化方法只能提取x方向和z方向的不连续边界信息,因此对于具有一定倾斜角度的不连续解往往将其重构为分片常数,称为著名的阶梯现象 [10]。为了克服传统TV正则化的不足,基于二阶偏导数信息的二阶TV正则化方法逐渐受到了学者的关注。二阶正则化方法不仅可以减弱一阶TV重构结果的阶梯现象,而且还能很好地保留解的边缘信息 [11] [12] [13] [14]。然而,与传统的TV正则化方法相比,在极小化的过程中,由于二阶TV正则化方法需要计算更多的一阶导数或二阶导数信息,导致计算量急剧增加 [15]。本文结合一阶TV正则化和二阶TV正则化方法各自的优点,提出了混合形式的正则化方法(HTV)。给出了二阶TV正则化方法的梯度计算方法,并基于2D的Marmousi2模型和Sigsbee模型进行数值实验,验证HTV方法的有效性。
2. 方法
2.1. 一阶TV正则化方法
TV正则化(一阶TV)能够有效提高反演的稳定性和重构的分辨率,且可以很好地保留解的边缘信息。1992年,Rudin首次提出了全变差正则化方法 [6]
(5)
其中,
表示积分区域,
,
分别表示模型参数关于x-和z -方向的偏导数。在(5)式中,由于函数
在原点处不可导,因此通常利用函数
近似
,
表示光滑参数,通常取固定值,本研究中取为
。于是全变分正则化惩罚项变为
(6)
为了对TV惩罚项进行离散,并引入记号
(7)
其中,
和
分别表示x-和z-方向的空间离散步长。于是,一阶TV正则化项的向前差分离散形式为
(8)
其中,
分别表示x-和z-方向的空间采样点数量。
由于一阶TV惩罚项具有保持解不连续的性质,其在图像处理和FWI中得到了广泛的应用。然而,对于具有一定倾角几何特征的重构问题,一阶TV正则化方法常常产生阶梯现象。
2.2. 二阶TV正则化方法
基于二阶导数信息的二阶TV惩罚项(TV2)具有获取参数的某些几何信息(不连续性、尖点等)的特性,因此,能够提高重构结果的分辨率。TV2惩罚项定义为 [12] [15]
(9)
其中,
表示积分区域,
分别表示模型参数关于x-和z-方向的二阶偏导数,
表示光滑参数,取为
。
类似地,为了对TV2惩罚项进行离散,引入如下变量
(10)
(11)
其中,
分别表示x-和z-方向的空间离散步长。于是TV2正则化惩罚项的中心差分离散格式为
(12)
在数值计算中,TV2能够很好地保留几何上具有一定倾角的解的不连续信息;然而,相对于TV正则化方法,由于TV2的高阶导数的高阶光滑特性使其对水平和垂直方向上的不连续信息具有光滑性,且TV2会引入额外的计算量,不利用于求解大规模反演问题。
2.3. 混合正则化方法
为了进一步提高算法的重构分辨率和计算效率,基于TV和TV2正则化方法各自的特性,本文提出了混合TV正则化方法和TV2正则化方法的正则化方法 (HTV)。为了调节不同方向上的不连续性信息的权重,采用
和
两个正则化参数,以控制TV和TV2在目标泛函中的权重。则HTV正则化的FWI目标函数为
(13)
需要注意的是,当
为0时, 式变为TV2正则化方法的目标函数; 当
为0时,(12)式为TV正则化方法的目标函数。
3. 目标函数的优化方法及梯度计算
3.1. 目标函数优化方法
在极小化目标函数(12)时,常见的优化方法有Newton型方法(如Gauss Newton, Truncated Newton等)和梯度型方法(如最速下降法,共轭梯度法)等 [16] [17] [18]。一般地,Newton型方法需要计算Hessian矩阵及其逆矩阵,需要大量的计算量和存储量。而梯度型算法,尤其是非线性共轭梯度算法(CG),其具有迭代格式简单、储存量小等优点,因此常用于求解大规模优化问题。
对于FWI反演问题,采用CG方法的参数更新格式为
(14)
其中,
为步长,
表示下降方向,
的迭代格式为
(15)
其中,
表示
在
处的梯度,
是共轭系数。当利用CG方法求解大规模优化问题时,当前迭代步的梯度
与之前的下降方向
满足正交性时,才能保证CG方法的快
速收敛性。然而,针对大规模高度非线性的FWI问题,该正交性往往很难得到保证。本文采用一种高效且带预处理的CG方法(CG-DESCENT)极小化目标函数(12)式 [16]。
当正交性不满足时,CG-DESCENT方法通过在一个子空间上求解一个子优化问题对该正交性进行恢复,因此,其具有较高的收敛速度和计算效率。因此,带预处理的CG-DESCENT方法由三个不同的迭代组成:一个是标准CG迭代,其共轭系数
为:
(16)
其中,
,
,在理论上,
是最佳选择;第二个是子空间迭代,当正交性失去时,
其通过L-BFGS方法在子空间上求解一个子优化问题来恢复正交性以提高算法的计算效率;第三个是预处理,当子空间迭代结束回到原空间时,将子空间得到的Hessian矩阵作为预处理矩阵来加速算法的收敛速度(见参考文献 [16])。
3.2. 梯度计算
利用CG-DESCENT求解FWI反演问题的一个关键因素时目标函数梯度的计算。首先考虑数据误差项的梯度计算,对(1)式中
的两端关于未知参数m进行微分,并利用微分的链式规则得
(17)
在上式中,
表示随算子的伴随,
是Jacobian矩阵。若对(17)式采用有限差分法直接计算Jacobian矩阵,则需要计算同参数数量相同的波场模拟,而这对于大规模FWI反演问题是不现实的,且随最计算规模的增加也不允许保存该大规模的Jacobian矩阵。为了避免计算Jacobian矩阵,本文采用一阶伴随方法计算数据残差项的梯度 [17] [18]
(18)
其中,
满足一阶伴随方程,即
(19)
从(18)和(19)式可以看出,计算数据残差项的梯度只需要求解两个正演问题,一个是计算正演波场u,另一个是计算伴随波场
。因此,利用伴随方法计算梯度是非常有效的。本文在频率域求解FWI问题时,每次迭代只取数据残差项梯度的实部。
为了求解TV的梯度,根据式(7)和(8),TV关于模型参数
的梯度表示为
(20)
其中,
(21)
由式(10),(11)及(12),TV2关于模型参数
的梯度表示为
(22)
其中,
(23)
式(23)适用于所有的内点,即对
和
,空间采样点的边界为
,
,
,
。
4. 数值实验
为了数值求解波动方程(3),首先采用混合网格有限差分法进行离散,形成线性方程组 [19]。在离散过程中,引入完全匹配层(PML)吸收边界条件以减少来自边界反射波场对波场的影响 [20]。基于MPI和OpenMP的混合并行框架求解该大规模稀疏线性方程组 [21]。
正则化参数控制目标函数的数据拟合项和正则化项之间的平衡。因此,正则化参数控制正则化解的特性的一个重要量,应谨慎选取这些参数。正则化参数越大,对应的正则化项占总目标函数比例越大,在相同优化方法和相同迭代步的条件下,所需要的计算量越大。在反演过程中,正则化参数
取为固定值,对于TV和TV2正则化方法,取
,
,对于HTV正则化方法,取
,
,该正则化参数通过实验获得,即根据TV和TV2反演结果选取该参数。基于Marmousi2模型和Sigsbee模型进行数值实验以验证HTV正则化方法的有效性,并分别与TV和TV2正则化方法进行对比以验证HTV的高效性。为了定量评估方法的计算表现,引入峰值信噪比指数(PSNR)指标 [22]
(24)
其中,
(25)
(26)
其中,
和
分别表示真实模型和重构模型。
4.1. Marmousi2模型
在地震成像问题中,Marmousi2模型是用来测试地震成像方法的基准模型之一。原始Marmousi2模型的模型参数为:深3.5 km,宽17 km,模型由199个地质层和一个450 m的深水层构成。为了减弱FWI问题的非线性性对算法的影响,在本文的实验中保持上表面的水层参数不更新。
 (a)
(a)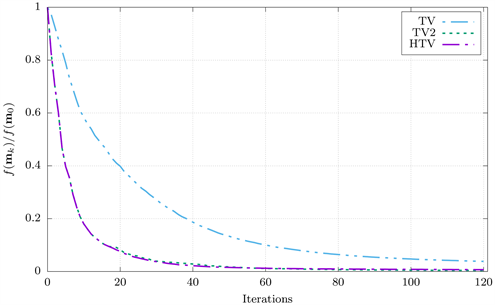 (b)
(b)
Figure 1. (a) The initial guess of the Marmousi2 model; (b) The convergence curve for three regularization methods
图1. (a) Marmousi2初始速度模型;(b) 三种正则化方法的收敛曲线
从数值计算角度考虑,在本实验中对原始模型进行重采样获得反演的真实模型。重采样的Marmousi2模型的模型大小为481 × 146,空间采样间隔为
,在反演区域四周均设置10个PML网格。因此,总的计算规模为
。图1(a)所示为重采样的Marmousi2真实模型,图2(a)为相应的初始模型,该初始模型由高斯滤波器对真实模型进行平滑化获得。
在反演过程中,115个震源和460个接收器均匀分布在模型的上表面。震源和接收器的间隔分别为80 m和20 m。反演过程中所使用的频率为3.0 Hz,4.5 Hz,6.0 Hz,7.5 Hz,9.0 Hz,10.5 Hz和12.0 Hz。对不同的正则化方法,均采用从低频到高频的逐次反演策略。每个频率的最大迭代次数设置为120次。如图1(b)所示为频率为3.0 Hz时,TV、TV2和HTV正则化方法的收敛曲线。图1(b)表明三种正则化方法均收敛,且相对于TV正则化方法,TV2和HTV的收敛速度明显快于TV正则化方法;TV2和HTV的收敛速度相当。
 (a)
(a)  (b)
(b)  (c)
(c)  (d)
(d)
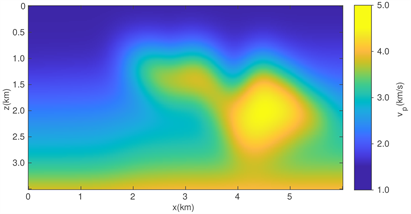
Figure 2. (a) The true velocity of the Marmousi2 model; (b) The reconstructed results of TV method; (c) The reconstructed results of TV2 method; and (d) The reconstructed results of HTV method
图2. (a) Marmousi2真实速度模型;(b) 表示TV方法的反演结果;(c) 表示TV2方法的反演结果;(d) 表示HTV方法的最终反演结果
图2所示为三种方法每个频率进行120次迭代后的最终的重构结果。图2(b)为TV正则化方法的反演结果,图2(c)为TV2正则化方法的反演结果,图2(d)为HTV正则化方法的反演结果。从图2可以看出,三种正则化方法均可较好地重构Marmousi2模型。从图2中还可以看出,当不连续边界较小且有一定的倾斜时,TV正则化方法的重构结果为阶梯形状,即产生与真实结果不相符合的虚假边界。TV2和HTV能够捕捉到斜面区域的不连续性,对具有倾斜的部分的重构表现比TV方法更好(如图2中椭圆区域)。
图3所示为模型在在不同水平位置(3.84 km,5.84 km和7.0 km)处的垂直剖面。图3再次说明了三种正则化方法均能较好地重构Marmousi2模型。从图2和图3中可以看出每种反演方法的重构分辨率随着深度的增加而降低,该现象是由于震源的有限照明所引起的。
 (a)
(a)  (b)
(b) 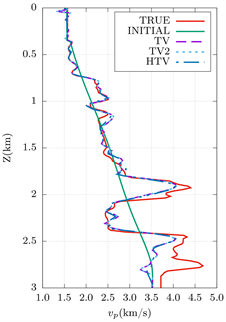 (c)
(c)
Figure 3. Vertical profiles for Marmousi2 model, TRUE-true model, INITIAL-background model, TV-TV regularization method, TV2-TV2 regularization method, HTV-hybridize TV and TV2: (a) at horizontal position of 3.84 km; (b) at horizontal position of 5.84 km; (c) at horizontal position of 7.0 km
图3. Marmousi2模型的垂直剖面图:TRUE-真实模型、INITIAL-初始模型、TV-TV正则化、TV2-TV2正则化、HTV-混合TV和TV2。(a) 在3.84 km的水平位置,(b) 在5.84 km的水平位置,(c) 在7.0 km的水平位置
表1为三种正则化方法的目标函数计算次数(NF),梯度计算次数(NG),峰值信噪比(PSNR)以及
的统计量对比。从表1可以看出,TV2和HTV在峰值信噪比指数方面要优于TV正则化方法,HTV正则化方法在目标函数估计次数与梯度计算次数方面优于TV2正则化方法,说明了混合HTV在在计算效率上优于TV2方法。

Table 1. Comparison between TV, TV2 and HTV regularization methods in the terms of the number of function estimations (NF), the number of gradient estimations (NG), and the peak signal-to-noise ratio (PSNR)
表1. TV,TV2和MTV正则化方法在目标函数估计次数(NF),梯度估计次数(NG)以及峰值信噪比(PSNR)的对比
4.2. Sigsbee模型
Sigsbee模型顶部构造分界面存在着强烈的速度间断,随着深度的加深以及背景介质速度的增加,会产生多散射场问题,给问题的求解提出了挑战。本节利用重采样的Sigsbee模型,其大小为391 × 144,空间采样间隔为
。为了减弱边界波场反射对重构结果的影响,在矩形区域边界添加10个网格的PML吸收层。因此,计算区域网格大小为411 × 166。图4(a)所示为对真实模型进行Gaussian光滑化所得到的初始模型,重采样的Sigsbee真实模型如图5(a)所示。
 (a)
(a) (b)
(b)
Figure 4. (a) The initial guess of the Sigsbee model; (b) The convergence curve for three regularization methods
图4. (a) Sigsbee初始速度模型;(b) 三种正则化方法的收敛曲线
在反演过程中,地表观测系统由97个震源和390个接收器组成,震源和接收器均匀分布在计算区域的上表面。21个离散频率从2.5 Hz到17.0 Hz进行采样,采样间隔为0.725 Hz。本实验也采用从低频到高频的反演策略逐次反演,每个频率的最大迭代步数为120步。如图4(b)所示为频率为2.5 Hz时,三种正则化方法的目标函数只
相对于迭代步的变化曲线。图4(b)表明对Sigsbee模型,三种正则化方法均收敛,且TV正则化方法的收敛速度与HTV正则化方法的收敛曲线基本一致。
 (a)
(a)  (b)
(b) 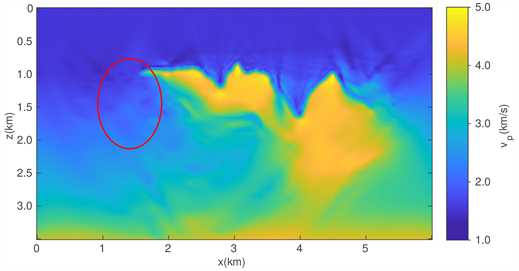 (c)
(c) 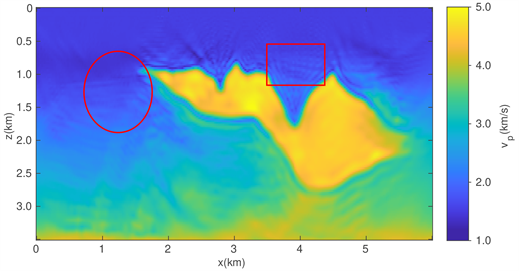 (d)
(d)
Figure 5. (a) The true velocity of the Sigsbee model; (b) The reconstructed results of TV method; (c) The reconstructed results of TV2 method; and (d) The reconstructed results of HTV method
图5. (a) Sigsbee真实速度模型;(b) 表示TV方法的反演结果;(c) 表示TV2方法的反演结果;(d) 表示HTV方法的最终反演结果
图5(b)~(d)所示分别为TV,TV2和HTV正则化方法的最终反演结果。图6(a)为速度模型在x = 2.49 km处的垂直剖面图,图6(b)为速度模型在x = 2.88 km处的垂直剖面图,图6(c)为速度模型在x = 4.5 km处的垂直剖面图。图5和图6说明三种正则化方法均可较好地重构Sigsbee模型。其次,TV2正则化方法相比于TV方法,在浅层的反演精度更高(如图5中椭圆区域所示)。与TV和TV2相比,HTV正则化方法能够准确的反演出高速比部分的Sigsbee模型(如图5中椭圆和矩形区域所示),说明HTV正则化方法是有效的。
 (a)
(a)  (b)
(b)  (c)
(c)
Figure 6. Vertical profiles for Sigsbee model: TRUE-true model, INITIAL-background model, TV-TV regularization method, TV2-TV2 regularization method, HTV-hybridize TV and TV2: (a) at horizontal position of 3.84 km; (b) at horizontal position of 5.84 km; (c) at horizontal position of 7.0 km
图6. Sigsbee模型的垂直剖面:TRUE-真实模型、INITIAL-初始模型、TV-TV正则化、TV2-TV2正则化、HTV-混合TV和TV2。(a) 在3.84 km的水平位置;(b) 在5.84 km的水平位置;(c) 在7.0 km的水平位置
为了说明HTV正则化方法在计算效率和重构分辨率方面的优势,对三种正则化方法的目标函数计算次数(NF),梯度计算次数(NG),峰值信噪比(PSNR)进行对比(见表2)。从表2中可以看出,相对于经典的TV和TV2正则化方法,HTV正则化方法具有较高的计算效率和重构精度。

Table 2. Comparison between TV, TV2 and HTV regularization methods in the terms of the number of function estimations (NF), the number of gradient estimations (NG), and the peak signal-to-noise ratio (PSNR)
表2. TV,TV2和MTV正则化方法在目标函数估计次数(NF),梯度估计次数(NG)以及峰值信噪比(PSNR)的对比
5. 结论与展望
全波形反演是一个大规模不适定问题,需要引入正则化方法以克服FWI问题的不适定性。本文基于一阶和二阶TV正则化方法,提出了一种混合的正则化方法(HTV)。HTV正则化方法能够克服传统TV正则化方法的阶梯现象,从而提高反演成像的分辨率。此外,引入了共轭梯度方法(CG-DESCENT)求解本文提出的正则化FWI问题。该算法可以恢复梯度和先前下降方向之间的正交性,提高算法的计算效率。基于Marmousi2模型和Sigsbee模型,从数值角度验证了HTV正则化方法的收敛性和高效性。数值结果表明,相对于TV和TV2正则化方法,HTV方法能够保留分段常数区域和倾斜区域的边界信息。
尽管数值实验表明,HTV正则化FWI方法相较于传统的方法重构精度要高,但仍有一些问题需要进一步研究:
1) 本文的正则化参数
和
设置为常数,并且效果良好。但是为了保持数据残差项和正则化项之间的平衡,正则化参数需要随着迭代次数的增减而动态变化。
2) 由于震源的有限照明,重构分辨率随着深度的增加而降低。然而这种现象可以通过使用适当的预处理或高阶优化方法来缓解。
因此,未来工作将系统地研究正则化参数的选取方法同时减少迭代的次数。此外,研究高阶优化方法(如Truncted-Newton,Gauss-Newton方法)和预处理方法来实现混合TV正则化FWI,也将是下一步的工作。
基金项目
本文获得国家自然科学基金(资助号:11801111)、贵州省科技计划项目([2019]1122)。
NOTES
*通讯作者。