1. 引言
1.1. 研究背景及意义
二项分布是统计问题中常见的离散型随机变量的分布,在实际生活中,很多现象都可以用二项分布进行描述,例如抛硬币得到正反面问题、彩票是否中奖、生男生女问题等。
事实上,在n次独立重复的伯努利(Bernoulli)试验中,设每次试验中事件A发生的概率为p。用X表示n重伯努利试验中事件A发生的次数,则X的可能取值为
,且对每一个
,事件
即为“n次试验中事件A恰好发生k次”,随机变量X的离散概率分布即为二项分布(Binomial distribution)。
此时n次试验中事件A恰好发生k次的概率由概率质量函数(Probability mass function)给出(盛骤等,1989) [1],如下:
根据上述公式可以看出,当n取值较小时,二项分布的计算难度一般,然而实例中,经常利用多次试验避免偶然性,因此n的取值通常较大,直接计算的工作量十分大,计算难度较高,需要使用简便高效的计算方法进行计算。
为了解决上述问题,国内外学者通常对二项分布采用基于泊松分布的近似方法以及基于中心极限定理的近似方法。本文主要基于中心极限定理研究二项分布的正态近似问题与正态近似中的若干条件。
正态分布(Normal distribution),也称“常态分布”,又名高斯分布(Gaussian distribution),最早由棣莫弗(Abraham de Moivre)在求二项分布的渐近公式中得到,是一个在数学、物理及工程等领域都非常重要的概率分布,在统计学的许多方面有着重大的影响力。
若随机变量X服从一个数学期望为
、方差为
的正态分布,记为
。其概率密度函数为正态分布的期望值
决定了其位置,其标准差
决定了分布的幅度。
对于一维正态分布,若随机变量X服从一个位置参数为
、尺度参数为
的概率分布,且其概率密度函数为
,则这个随机变量就称为正态随机变量,正态随机变量服从的分布就称为正态分布,记作
,读作X服从
,或X服从正态分布。
n维随机向量具有类似的概率规律时,称此随机向量遵从多维正态分布。多元正态分布有很好的性质,例如,多元正态分布的边缘分布仍为正态分布,它经任何线性变换得到的随机向量仍为多维正态分布,特别它的线性组合为一元正态分布。当
,
时,正态分布就成为标准正态分布。
基于正态分布良好的性质,许多学者在研究统计模型时通常采用正态近似进行探究。
1.2. 国内外研究
1.2.1. 用泊松分布近似二项分布
二项分布作为统计问题中常见的离散型随机变量的分布,应用十分广泛,但是由于n的取值通常较大,计算难度较高,需要更为高效的计算方法。在一定条件下,依托泊松定理,可以用泊松分布近似二项分布。
在马小霞(2007)的研究中 [2],当参数间的关系为
时,二项分布的极限分布是泊松分布。这里要求n充分大时,np不大或
不大,也就是p比较小,才能得到比较精确的近似值。
在侯国亮(2018)的研究中 [3] 曾提到,在实践中,一般当
,
时,用
作为
的近似值效果较好。
吴艳华(2012)曾依据试验数据说明 [4],当n很大p很小且
时,用泊松近似比正态近似效果要好,并且当
,
时,二项分布的泊松近似精度更高。这一结论在侯国亮(2018) [3] 针对具体问题的研究中也得到了印证。在李斐等(2020) [5] 的研究中,也对两种近似的收敛速度进行了比较,可以根据不同的参数条件,选择较为适合的近似方法。
相对于泊松近似对n较大、p较小的要求,正态近似只要求n充分大,因此二项分布的正态近似普适性更强,且正态分布性质较好,有许多学者也针对其进行了更深层次的研究。
1.2.2. 用中心极限定理近似二项分布
对于独立同分布的随机变量,中心极限定理如下:
设随机变量
独立同分布,并且具有有限的数学期望和方差:
,
,则对任意x,分布函数
,满足
该定理说明,当n很大时,随机变量
近似地服从标准正态分布
。因此,当n很大时,
近似地服从正态分布
。
该定理是中心极限定理最简单又最常用的一种形式,在实际工作中,只要n足够大,便可以把独立同分布的随机变量之和当作正态变量。这种方法在数理统计中用得很普遍,当处理大样本时,它是重要工具。
如果n足够大,那么分布的偏度就比较小。在这种情况下,如果使用适当的连续性校正,那么
的一个很好的近似是正态分布:
。
不同的经验法则可以用来决定n是否足够大,以及p是否距离0或1足够远,盛骤等(1989)描述为 [4]:当n充分大时,可作近似计算。在《概率统计》(2000) [6] 一书中则定义为:正态分布作近似计算,它的优点是不受“
”限制,只要n足够大即可。
其中一个常用的规则是np和
都必须大于5。当n越大(至少20)且p不接近0或1时近似效果更好。
Chang et al. (2006, 2008)表明 [7] [8],应用中心极限定理时,样本大小应随概率分布类型而变化。
2. 研究内容及研究方法
为了探究不同的n与p对近似效果的影响,本文利用统计模拟衡量不同条件下近似值与精确值之间的差距。
对独立重复的二项分布实验,每次发生概率为p的事件A的总次数
,若n次独立重复实验中事件A发生k次,此时
,以此可以求得二项分布下的精确概率值
。
对于上述实验,本文中按照正态近似公式求得此时
,如下:
,即
。
这里可以利用相对误差衡量
与
之间的差距,如下:
3. 统计模拟
对
范围内步长为10的每一n值相应的不同参数
时的概率
进行了大量的对比计算,文中仅给出部分计算结果,见表1,同理可以做概率
时的对比计算。

Table 1. Relative error and corresponding k value of normal approximation
with different parameters n and p
表1. 不同参数n,p正态近似
的相对误差及相应k值
通过计算分析得出:
1) n值相同,p值不同时,近似计算的准确性并不相同。在
达到范围内,p越接近0.5,近似计算的准确性越高,即
时的近似效果最好。由二项分布的特点可知,
范围内,近似计算的准确性变化与上述相同。二项分布只在
时为对称分布,此时,用正态近似准确性最高 [9]。
2) 对于
接近于0时,k值在随机变量的均值np附近相对误差较小,近似计算的准确性较高。但需注意
接近于0时,单纯通过相对误差的数值不能确切说明近似程度,还应看
本身概率值的大小。
3) 对于不同参数n、p时,正态近似
的最大绝对误差(近似值与精确值之差的绝对值)及相应的k值,见表2,仅给出部分结果;当允许误差不超过0.004时,不同参数p正态近似所需n的最小下限值见表3。
可以发现,当
或
时,要达到好的近似效果,正态近似所需n很大,此时应考虑其他方法进行近似。

Table 2. Absolute error and corresponding k value of normal approximation
with different parameters n and p
表2. 不同参数n,p正态近似
的绝对误差及相应k值

Table 3. The minimum lower limit of n required for normal approximation of different parameters p
表3. 不同参数p正态近似所需n的最小下限值
例如图1,当
,
时,将精确值用线(红色)连接起来可以看到,其形状和近似值(蓝色)较为相近,并且在
处的绝对误差最大,并逐渐趋向于0。

Figure 1. The exact value and approximate value of
when n = 50, p = 0.1 after normal approximation continuity, the exact value and approximate value of k
图1. 正态近似连续性修正后n = 100,p = 0.01时,
的精确值与近似值
例如图1,当n = 50,p = 0.1时,将精确值用线(红色)连接起来可以看到,其形状和近似值(蓝色)较为相近,并且在
处的绝对误差最大,并逐渐趋向于0。
由上述图表可以看出,通过中心极限定理对二项分布进行正态近似的效果较为明显,但是误差仍然波动不定。这里对正态近似进行连续性修正,即
。同样可以利用MATLAB实现对修正后公式的误差验证。
这里只展示n = 100,p = 0.01时的情况。
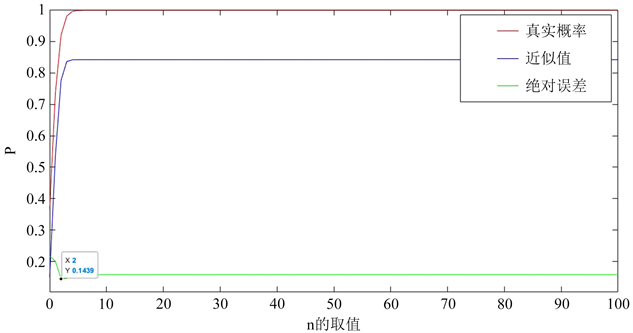
Figure 2. The exact value and approximate value of
when n = 100, p = 0.01 after normal approximation continuity
图2. 正态近似连续性修正后n = 100,p = 0.01时,
的精确值与近似值

Figure 3. The exact value and approximate value of
when n = 100, p = 0.01 after normal approximation continuity
图3. 正态近似连续性修正后n = 100,p = 0.01时,
的精确值与近似值
如图2所示,修正后,当n = 100,p = 0.01时,对于概率
在
时误差最小为0.1439,此后基本趋于平缓。而图3中,在修正后,当n = 100,p = 0.01时,对于概率
在
时误差最大为0.05617,此后误差逐渐减小。可以看出,修正后的精确值与估计值较为吻合,近似效果较好。
4. 结论和讨论
4.1. 研究的结论
在过往的理论学习中,二项分布的正态近似只要求n充分大,而通过统计模拟后可以看出,在n相对较大时,参数p及随机变量取值k的不同对近似计算准确性的影响是比较明显的。
对于不同参数p,n值充分大的程度不同,为了更好地得到近似的结果,应用时可参考文中给出的不同p所需n的最小下限值。
当
或
时,要达到好的近似效果,正态近似所需n很大,此时应考虑其他方法进行近似。
二项分布使用正态近似时可以通过使用连续性修正近似公式,以此来提高近似的效果及计算的准确度。
4.2. 研究的局限性
本文有以下几个不足之处:1) 实际生活中,某一具体事件发生的概率并不一定是可知的,因此在概率p的确定上会有一些浮动,对最终n的取值也会有一定的影响,因此文中所给的n的最小下限值仅供参考。2) 文中的方法对随机变量k的不同取值及其对n的最小下限值影响的探究效果不明确,需要更好的方法进行持续的研究。