1. 引言
群的一个重要问题是决定一些不同阶群的结构类型,也就是群的同构分类问题,而群的结构重要分为两大类,一类群是交换群,此时它同构于循环群或者一些循环群的直积。第二类群是非交换群,这需要根据一个群阶的大小来推断出元素之间的关系,从而决定出群的结构,因此给出不同阶群的结构就有了实际意义和理论价值。
半群的结构的研究已经有了一些成果,具体参见周绍艳(2016) [1] 和刘心驰(2012) [2]。对于一般有限群的研究,梁静老师在文献 [3] 中对
群的结构进行了归纳;孙雨晴,卢家宽老师在文献 [4] 中给出了自中心化子群对有限群结构的影响;陈梦,刘正龙,陈贵云老师在文献 [5] 中给出了最高阶元的阶为7及Sylow2-子群的阶为8的有限群的结构;夏晶老师在文献 [6] 中给出了有限群的阶与群的结构,而本文利用西罗定理,通过群扩张定理,给出了pq阶群两种可能的结构和4p阶群五种可能的结构。
2. 预备知识
本节主要给出了一些本文中要用到的一些定义和定理。
定义1.1 [7] 称群G为p-群,如果群G的每个元素皆为p-元素。
定义2.1 [7] 称p-群S为群G的Sylowp-子群,如果S是G的极大p-子群,即不存在G的p-子群
。
引理1 [7] 群G中Sylowp-子群的个数
是
的因子,并且
。
引理2 [7] 设
,则
同构于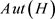 的一个子群。
的一个子群。
引理3 [8] 设
为正整数,G是n阶循环群N被m阶循环群F的扩张,则G有如下区定义关系:
,
,
,
,其中
,
。
3. 决定几类不同阶的群结构
我们已经知道
时
,
时
或
,下面我们决定其余几类不同阶的群结构。
定理1设
,其中
为素数,则G则只有以下几类结构。
1) G交换
,
2) G非交换
。
证明:设
,若G交换,则
。
1) 若G非交换,我们设
,
。
由于
均为素数,所以
均为循环群。不妨设
,
,
。
由西罗定理可得:
,又因为
,所以可得
即
。
,显然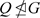 (否则
,
,
,
,可得
且G可交换,矛盾),所以
,即
,也即
,所以
,不妨设
,
,则
。
(否则
,
,
,
,可得
且G可交换,矛盾),所以
,即
,也即
,所以
,不妨设
,
,则
。
又因为
,所以
,即
,
所以
。
综上G有两种结构:
1) G交换
,
2) G非交换
。
定理2设
,其中
为素数,则G则只有以下几类结构。
1)
或者
,
2)
,
3)
,
4)
,
5)
。
证明:设
,若G交换,则1)
或者2)
。
若G非交换,我们设
。由于
均为素数,所以由西罗定理可得:G的Sylowp-子群的个数
的,又因为p为素数,所以可得
即
。对P用
定理,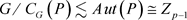 。由于
,故
或
。
。由于
,故
或
。
若
,则G为
被
的扩张。由引理3,
且有定义关系:
,
,
,其中
,
。
由于G非交换,解上述同余式得
,
或
。
由此得到两个群:
i)
,
ii)
。
若
,则G为
被
的扩张。由引理3,
且有定义关系:
,
,
,其中
,
。
由于G非交换,解上述同余式得
,
或
。
由若
,
则G同构于上述ii)型群。这样得到一个与上述群不同构的群:
iii)
。
综上4p阶群分类如下:
G为交换群
或者
。
G为非交换群
i)
,
ii)
,
iii)
。