35 kV电力电缆快插接头关键内部结构设计研究

Research on Key Internal Structure Design of 35 kV Power Cable Quick-Connect Joint

摘要: 在35 kV电力电缆快插接头结构设计中，接头内部电场主要靠两端应力锥结构和中间内屏蔽层结构进行处理，避免接头内部出现局部电场强度过高，导致接头高压击穿。本文通过maxwell有限元分析方法，仿真出应力锥和内屏蔽层在不同的设计参数下，接头内部的电场大小及分布情况，找出应力锥和内屏蔽层设计的最优解，为将来此类产品提供设计选择。

Abstract: In the structural design of 35 kV power cable quick-plug joint, the internal electric field of the joint is mainly handled by the stress cone structure at both ends and the inner shielding layer structure in the middle to avoid local high electric field intensity inside the joint, resulting in high voltage breakdown of the joint. In this paper, the maxwell finite element analysis method is used to simulate the magnitude and distribution of the electric field inside the joint under different design parameters of the stress cone and the inner shielding layer, and find the optimal solution for the design of the stress cone and the inner shielding layer, which is the best solution for the future. Products offer design options.

1. 引言

高压电力电缆接头是电缆与电缆相连的重要部件。高压电力电缆主要由导电线芯、内屏蔽层、绝缘层、外屏蔽层等结构组成，电缆连接技术主要是将这些结构重新恢复，但现有的技术无法完美的将这些结构恢复成电缆出厂状态，所以电缆连接处往往在高电压下出现电场畸变，造成电场局部场强过高，引发绝缘击穿事故。为了确保运行稳定性，在电缆接头设计过程中一个重要的设计目标就是降低接头内部电场场强，通常的做法是在接头屏蔽切断处设计应力锥结构及在金属导体连接处设计内屏蔽层 [1]。

在实际设计过程中，受接头形式、电缆结构等因素影响，会导致其在应力锥及内屏蔽的形状、大小及边缘倒角等细节设计发生变化，这些不同之处决定着其改善电场的能力，如果应力锥和内屏蔽结构细节处理不到位，将会直接影响产品的性能 [2]。

2. 应力锥的设计方法

2.1. 应力锥设计的要素

应力锥结构是电缆附件中用来处理电缆接头绝缘屏蔽层切断点处电场的经典结构，其应用在电缆绝缘屏蔽层切断点附近，将其延伸，使零电位形成喇叭状，改善电场分布。应力锥处理电场的能力受三个要素影响，分别为：材料电阻率、轴向长度和张开角度。

2.2. 应力锥的仿真

本文选择设计对象为35 kV电力电缆快插接头，其应力锥设计结构图见图1所示，通过设置应力锥不同的材料电阻率、轴向长度和张开角度，根据仿真的电场分布变化，探索应力锥处理电场最佳设计参数值。

Figure 1. Structure diagram of stress cone of quick-plug joint of 35 kV power cable

图1. 35 kV电力电缆快插接头应力锥处结构图

根据一般设计经验，应力锥材质为半导体材质，其电阻率ρ取值范围为：10⁴~10⁸ Ω·m [3]，轴向长度L范围为：40~120 mm；应力锥张开角度θ范围为：5˚~30˚。应力锥处结构图见图1。

1) 取应力锥电阻率ρ和长度L为固定最小值保持不变，张开角度θ从5˚~30˚不断变化时，仿真电力电缆快插终端头应力锥处的电场大小：

a) ρ = 10⁴ Ω·m，L =40 mm，θ = 5˚时，应力锥处的电场最大值E_max = 24.936 MV/m，见图2所示。

Figure 2. Electric field at the stress cone of 35 kV power cable push-in joint

图2. 35 kV电力电缆快插接头应力锥处电场

b) ρ = 10⁴ Ω·m，L =40 mm，θ = 10˚时，应力锥处的电场最大值E_max = 24.161 MV/m，见图3所示。

Figure 3. Electric field at the stress cone of the 35 kV power cable push-in connector

图3. 35 kV电力电缆快插接头应力锥处电场

c) ρ = 10⁴ Ω·m，L =40 mm，θ = 15˚时，应力锥处的电场最大值E_max = 24.928 MV/m，见图4所示。

Figure 4. Electric field at the stress cone of the 35 kV power cable push-in connector

图4. 35 kV电力电缆快插接头应力锥处电场

d) ρ = 10⁴ Ω·m，L =40 mm，θ = 20˚时，应力锥处的电场最大值E_max = 25.717 MV/m，见图5所示。

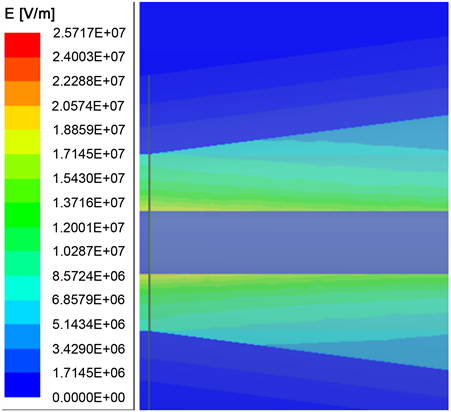
Figure 5. Electric field at stress cone of 35 kV power cable push-in joint

图5. 35 kV电力电缆快插接头应力锥处电场

由上述a)、b)、c)、d)仿真结果见图6所示可以得出：应力锥的张开角度θ = 10˚时E_max最小，处理电场能力最强。

Figure 6. Influence of stress cone opening angle on the magnitude of electric field

图6. 应力锥张开角度对电场大小的影响

2) 取应力锥电阻率ρ为固定最小值、张开角度θ为10˚不变，而应力锥轴向长度L不断变化时，仿真电力电缆快插接头应力锥处的电场大小：

a) ρ = 10⁴ Ω·m，L = 60 mm，θ = 10˚时，应力锥处的电场最大值E_max = 24.126 MV/m，见图7所示。

Figure 7. Electric field at the stress cone of 35 kV power cable push-in connector

图7. 35 kV电力电缆快插接头应力锥处电场

b) ρ = 10⁴ Ω·m，L = 80 mm，θ = 10˚时，应力锥处的电场最大值E_max = 21.692 MV/m，见图8所示。

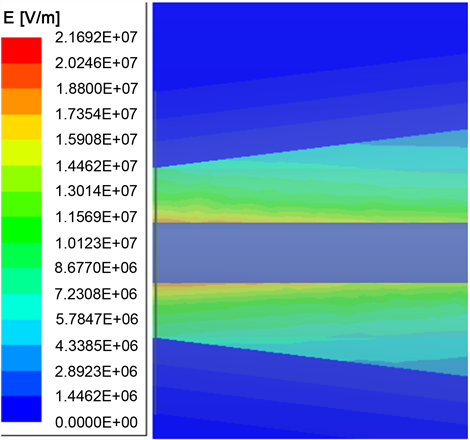
Figure 8. Electric field at the stress cone of the 35 kV power cable push-in connector

图8. 35 kV电力电缆快插接头应力锥处电场

c) ρ = 10⁴ Ω·m，L = 100 mm，θ = 10˚时，应力锥处的电场最大值E_max = 21.575 MV/m，见图9所示。

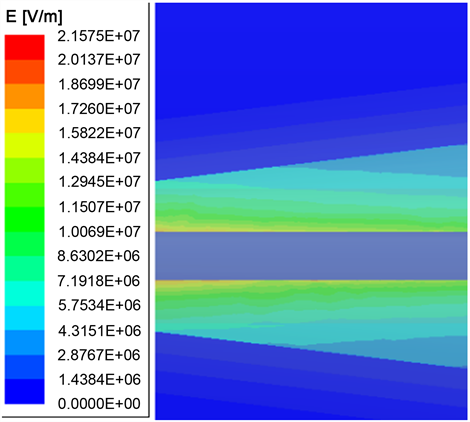
Figure 9. Electric field at the stress cone of the 35 kV power cable push-in connector

图9. 35 kV电力电缆快插接头应力锥处电场

d) ρ = 10⁴ Ω·m，L = 120 mm，θ = 10˚时，应力锥处的电场最大值E_max = 21.169 MV/m，见图10所示。

Figure 10. Electric field at the stress cone of the 35 kV power cable push-in connector

图10. 35 kV电力电缆快插接头应力锥处电场

由上述a)、b)、c)、d)仿真结果见图11所示可以得出：应力锥长度L越大，E_max越小，处理电场能力越强。但L的长度在设计时不可能无限大(受到产品安装尺寸和内爬电距离双重制约)，而且L > 80 mm以后E_max值变化不大，所以根据实际应用经验和仿真结果，L = 80 mm是一个比较合适的设计数值。

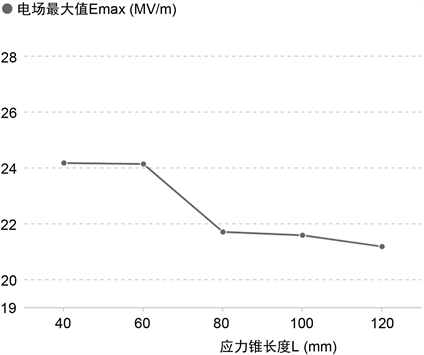
Figure 11. Influence of stress cone length on electric field magnitude

图11. 应力锥长度对电场大小的影响

3) 取应力锥张开角度θ为10˚、应力锥轴向长度L为80 mm不变，而应力锥电阻率ρ不断变化时，仿真电力电缆快插接头应力锥处的电场大小：

a) ρ = 10⁵ Ω·m，L = 80 mm，θ = 10˚时，应力锥处的电场最大值E_max = 21.107 MV/m，见图12所示。

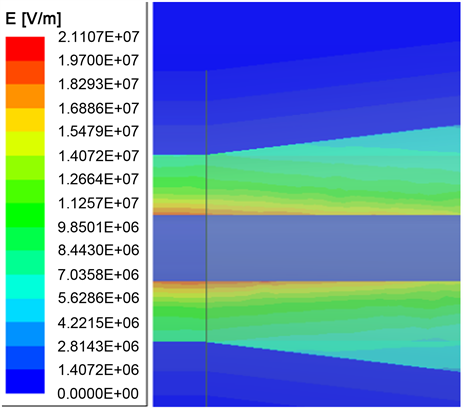
Figure 12. Electric field at the stress cone of the 35 kV power cable push-in connector

图12. 35 kV电力电缆快插接头应力锥处电场

b) ρ = 10⁶ Ω·m，L = 80 mm，θ = 10˚时，应力锥处的电场最大值E_max = 21.077 MV/m，见图13所示。

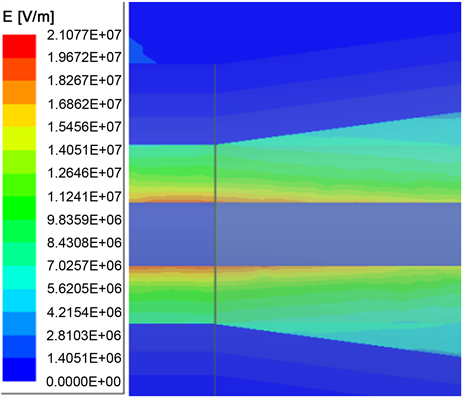
Figure 13. Electric field at the stress cone of the 35 kV power cable push-in connector

图13. 35 kV电力电缆快插接头应力锥处电场

c) ρ = 10⁷ Ω·m，L = 80 mm，θ = 10˚时，应力锥处的电场最大值E_max = 26.664 MV/m，见图14所示。

Figure 14. Electric field at the stress cone of the 35 kV power cable push-in connector

图14. 35 kV电力电缆快插接头应力锥处电场

d) ρ = 10⁸ Ω·m，L = 80 mm，θ = 10˚时，应力锥处的电场最大值E_max = 28.753 MV/m，见图15所示。

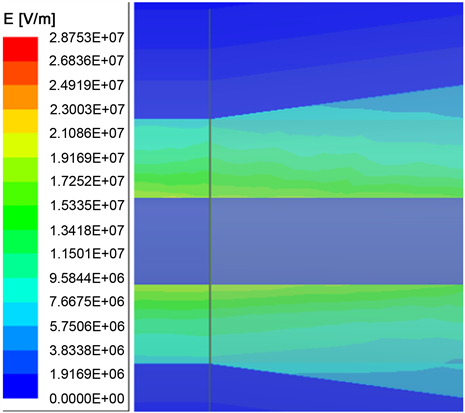
Figure 15. Electric field at the stress cone of the 35 kV power cable push-in connector

图15. 35 kV电力电缆快插接头应力锥处电场

由上述a)、b)、c)、d)仿真结果见图16所示可以得出：当应力锥电阻率ρ大于10⁶ Ω·m后，E_max大大增加，其处理电场能力会明显下降。

Figure 16. Effect of stress cone resistivity on electric field magnitude

图16. 应力锥电阻率对电场大小的影响

2.3. 应力锥的仿真小结

从1)、2)、3)各项仿真结果见表1：当应力锥的张开角度小于10˚时；应力锥轴向越长时；应力锥电阻率不大于10⁶ Ω·m时，其处理电场能力最强。

Table 1. Summary of electric field simulation at stress cone

表1. 应力锥处电场仿真汇总

3. 屏蔽层的设计方法

3.1. 屏蔽层设计的要素

在电缆接头制作过程中，导体的连接一般采用压接方式连接 ，这就导致导体表面不光滑，从而引起表面电场强度增加。所以电缆接头设计时都会设置内屏蔽层，用来平行包覆在内部导体表面上，使绝缘和导体有良好的接触，来消除导体表面不光滑的影响。由于内屏蔽层材质为半导体橡胶材质可近似看成导体，其表面光滑程度和边角处的处理情况也必然影响到电场强度大小；另外试验表明内屏蔽层覆盖导体的长度也会影响接头内电场强度。

由于电缆接头内屏蔽层均是由模具注橡生产而成，模具表面经过抛光处理，即屏蔽层的表面光滑程度满足要求，所以内屏蔽层的设计要素有：电阻率、轴向长度和边缘边角的倒角大小。内屏蔽层和应力锥材质相同，其电阻率ρ在应力锥仿真时已经确定不应大于10⁶ Ω·m，下面只针对内屏蔽层的轴向长度和边缘倒角大小进行仿真分析。

3.2. 屏蔽层的仿真

35 kV电力电缆快插接头的内屏蔽层设计结构见图17所示，设置不同的内屏蔽层轴向长度和边缘倒角大小，根据仿真的电场分布变化，探索内屏蔽层处理电场最佳时的各项参数 [4] [5]。

由于各种电缆接头大小不一样，其内屏蔽长度也不一样，无法直接确定内屏蔽层长度，所以本次仿真取内屏蔽层与导体的长度差值ΔL变化进行，选择ΔL取值范围为：−4~6 mm；内屏蔽层边缘倒角半径R取值范围为0~3 mm。

Figure 17. Structural diagram of the inner shield of the 35 kV power cable quick-plug connector

图17. 35 kV电力电缆快插接头内屏蔽处结构图

1) 取内屏蔽层与导体的长度差值ΔL为0固定不变、倒角半径不断变化时，仿真电力电缆快插接头内屏蔽层处的电场大小：

a) ΔL = 0 mm，R = 0 mm、即不倒角时，内屏蔽层处的电场最大值E_max = 26.260 MV/m，见图18所示。

Figure 18. Electric field at the inner shield of 35 kV power cable quick-plug connector

图18. 35 kV电力电缆快插接头内屏蔽处电场

b) ΔL = 0 mm，R = 0.5 mm，内屏蔽层处的电场最大值E_max = 25.693 MV/m，见图19所示。

Figure 19. Electric field at the inner shield of 35 kV power cable quick-plug connector

图19. 35 kV电力电缆快插接头内屏蔽处电场

c) ΔL = 0 mm，R = 1 mm，内屏蔽层处的电场最大值E_max = 23.291 MV/m，见图20所示。

Figure 20. Electric field at the inner shield of 35 kV power cable quick-plug connector

图20. 35 kV电力电缆快插接头内屏蔽处电场

d) ΔL = 0 mm，R = 1.5 mm，内屏蔽层处的电场最大值E_max = 22.705 MV/m，见图21所示。

Figure 21. Electric field at the inner shield of 35 kV power cable quick-plug connector

图21. 35 kV电力电缆快插接头内屏蔽处电场

e) ΔL = 0 mm，R = 2 mm，内屏蔽层处的电场最大值E_max = 21.180 MV/m，见图22所示。

Figure 22. Electric field at the inner shield of 35 kV power cable quick-plug connector

图22. 35 kV电力电缆快插接头内屏蔽处电场

f) ΔL = 0 mm，R = 3 mm，内屏蔽层处的电场最大值E_max = 21.127 MV/m，见图23所示。

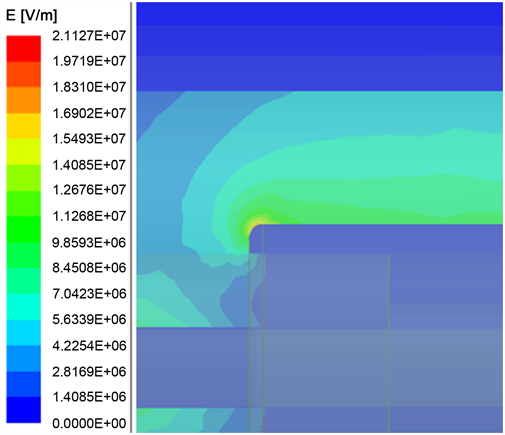
Figure 23. Electric field at the inner shield of 35 kV power cable quick-plug connector

图23. 35 kV电力电缆快插接头内屏蔽处电场

由上述a)、b)、c)、d)、e)、f)仿真结果见图24所示可以得出：内屏蔽层倒角半径R越大E_max越小，在R大于1 mm后，E_max明显减小，R超过2 mm后，E_max趋于一个较小值稳定。

Figure 24. Influence of chamfering of inner shielding layer on the magnitude of electric field

图24. 内屏蔽层边角倒角对电场大小的影响

2) 取内屏蔽层导体倒角半径R = 2 mm，ΔL不断变化时，仿真电力电缆快插接头内屏蔽层处的电场大小：

a) ΔL = −4 mm，R = 2 mm时，内屏蔽层处的电场最大值E_max = 25.318 MV/m，见图25所示。

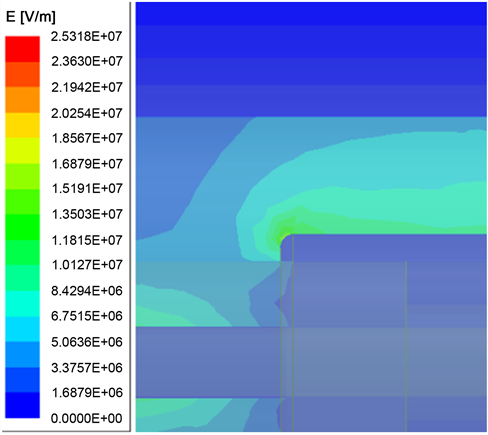
Figure 25. Electric field at the inner shield of 35 kV power cable quick-plug connector

图25. 35 kV电力电缆快插接头内屏蔽处电场

b) ΔL = −2 mm，R = 2 mm时，内屏蔽层处的电场最大值E_max = 24.423 MV/m，见图26所示。

Figure 26. Electric field at the inner shield of 35 kV power cable quick-plug connector

图26. 35 kV电力电缆快插接头内屏蔽处电场

c) ΔL = 2 mm，R = 2 mm时，内屏蔽层处的电场最大值E_max = 20.674 MV/m，见图27所示。

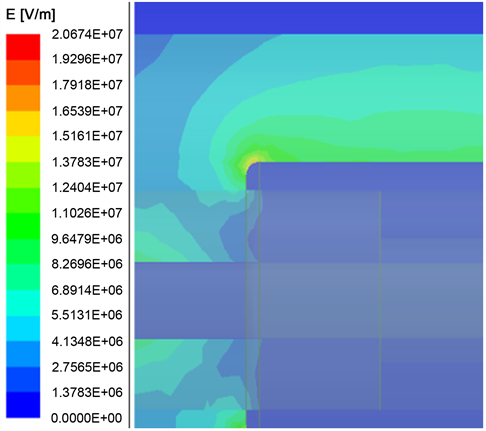
Figure 27. Electric field at the inner shield of 35 kV power cable quick-plug connector

图27. 35 kV电力电缆快插接头内屏蔽处电场

d) ΔL = 4 mm，R = 4 mm时，内屏蔽层处的电场最大值E_max = 18.992 MV/m，见图28所示。

Figure 28. Electric field at the inner shield of 35 kV power cable quick-plug connector

图28. 35 kV电力电缆快插接头内屏蔽处电场

e) ΔL = 6 mm，R = 2 mm时，内屏蔽层处的电场最大值E_max = 18.990 MV/m，见图29所示。

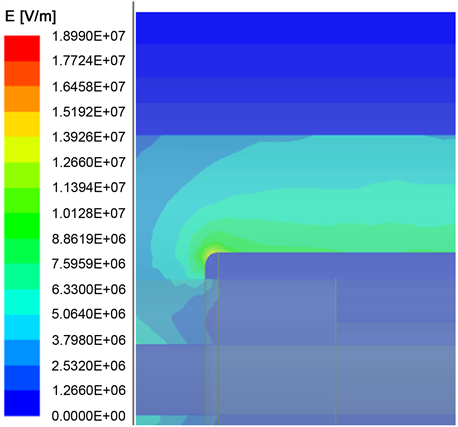
Figure 29. Electric field at the inner shield of 35 kV power cable quick-plug connector

图29. 35 kV电力电缆快插接头内屏蔽处电场

由上述a)、b)、c)、d)、e)仿真结果见图30所示可以得出：内屏蔽层长度与导体长度差值ΔL越大，内部电场E_max越小，当ΔL > 4 mm后，E_max趋于稳定。

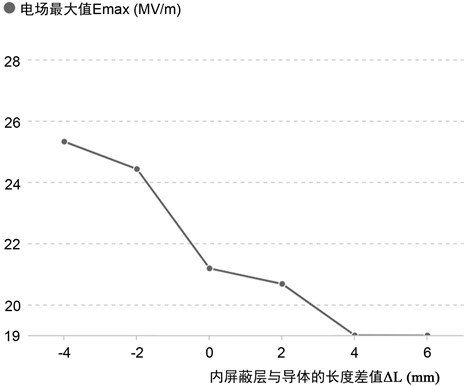
Figure 30. Influence of the difference between the inner shielding layer and the conductor length on the magnitude of the electric field

图30. 内屏蔽层与导体长度差值对电场大小的影响

3.3. 屏蔽层的仿真小结

从1)、2)各项仿真结果见表2：当内屏蔽层倒角半径R ≥ 2 mm、内屏蔽层长度与导体长度差值ΔL ≥ 4 mm时；其处理电场能力最强。

Table 2. Summary of electric field simulation at inner shielding layer

表2. 内屏蔽层处电场仿真汇总

4. 设计试验验证

在初次设计35 kV电力电缆快插接头过程中，因为未做全面性仿真，设计时依据10kV电力电缆快插接头的设计经验，应力锥的材料电阻率ρ = 10⁶ Ω·m、轴向长度L = 112 mm和张开角度θ = 8.5˚；内屏蔽层边角倒角半径R = 1 mm，内屏蔽层长度与导体长度差值ΔL = 1.5 mm。

设计的产品在场内初次试验时，工频耐压试验出现了30%样品击穿，如此高的击穿几率，属于不正常现场，故对击穿事件进行分析。分析发现击穿产品的击穿点均在同一个位置，且该位置正好处于内屏蔽层包裹导体的边缘处，见图31所示。

Figure 31. 35 kV Electric power cable express the connect point

图31. 35 kV电力电缆快插接头击穿点

通过击穿点位置可以确定应力锥的设计没有问题，击穿原因与内屏蔽层的设计有必然关系。随后检查最初设计图纸，结合本文分析内屏蔽层的设计要素，发现内屏蔽层设计边角倒角半径R和内屏蔽层长度与导体长度差值L的取值都不合适，导致内屏蔽层处内部电场较大，易发生击穿。

为了验证上述分析的原因是否正确，将内屏蔽层图纸进行修改，将R更改为2 mm，ΔL更改为4 mm，随之也根据尺寸将生产的模具进行对应修改。

修改后再进行生产试验验证，试验合格率达到了100%，随后送往第三方检测机构进行型式试验。

由35 kV电力电缆和35 kV电力电缆快插接头组成的试品，依据GB/T12706.4试验标准完成型式试验。部分结果列入表3中。

Table 3. Type test results of 35 kV power cable push-in connector

表3. 35 kV电力电缆快插接头型式试验结果

表3结果证实：设计修改后的35 kV电力电缆快插接头的电气性能符合标准要求，接头内部电场得到了有效处理。

5. 结论

本文通过maxwell有限元分析方法，仿真出35 kV电力电缆快插接头的应力锥和内屏蔽层在不同的设计参数下，接头内部的电场大小及分布情况，找出应力锥和内屏蔽层设计的最优设计值，并通过试验进行了验证，证明：

35 kV电力电缆接头应力锥设计的张开角度θ = 10˚时，E_max最小；应力锥长度L越大，E_max越小，L > 80 mm，E_max值变化减少；

35 kV电力电缆接头的应力锥和内屏蔽层所用材料的电阻率ρ大于10⁶ Ω·m后，E_max会明显下降；

35 kV电力电缆接头的内屏蔽层设计中屏蔽管边缘倒角半径R越大，E_max最小；在R大于1 mm后，处理电场能力明显增强，R超过2 mm后，E_max变化趋于稳定；内屏蔽层长度与导体长度差值ΔL越大，处理电场能力越强，当ΔL > 4 mm后，趋于稳定。

基金项目

南方电网高海拔地区35 kV架空输电线路旁路带电作业关键技术与装备研究项目(YNKJXM20210110)。

参考文献