MATLAB可视化技术在工程优化设计中的应用研究

Visualization Technology on Engineering Optimal Design Based on MATLAB

摘要: 工程优化设计是在给定的各种约束条件下合理确定各设计参数，从众多的工程设计方案中搜寻到目标为最佳的设计方案，使某项或几项工程设计指标获得最优值。可视化技术随着计算机技术的应用越来越被关注，可视化技术与工程优化设计的结合是近年来的研究热点之一。本文从工程优化设计的可行域、一维优化问题和多维优化问题出发，以案例为依托，结合MATLAB可视化技术开展研究，为解决实际工程问题创造了条件。

Abstract: Engineering optimization design is to determine the design parameters reasonably under the given constraints, search for the best design plan from many engineering design plans, and obtain the optimal value of one or several engineering design indexes. With the application of computer technology, more and more attention has been paid to visualization technology. The combination of visualization technology and engineering optimization design is one of the research hot-spots in recent years. In the paper, visualization technology to optimal design is studied with the feasible domain of engineering optimal design problem, single variable minimization and multi-variable minimization, combined with cases and MATLAB practices, to create conditions for solving practical engineering problems.

1. 引言

人类从事的一切生产活动都离不开设计。设计是为满足社会需要进行的一系列创造性思维活动，是把各种先进的科学技术转化为生产力的重要手段，设计就是创新。对工业企业来说，设计决定着企业的命运和前途。因为现代企业的竞争，实质上是产品性能和质量的竞争，而产品的性能和质量主要是通过设计来实现并保证的，如同生物体的基本性态是在其胚胎基因的遗传和重组过程中就确定一样。

工程优化设计是随着计算机技术的迅速发展和广泛应用而产生的一种现代设计方法 [1] [2]。工程优化设计是将工程设计问题转化为优化设计问题，利用数学规划方法，借助于计算机高速度、高精度和大存储量的运算处理能力，从满足工程设计要求的一切可行方案中自动寻求最佳设计方案的设计方法。它能够综合处理并最大限度地满足各种不同性质甚至相互矛盾的设计要求，迅速而准确地得到满意的设计结果，且可用于各种工程项目的方案设计和技术设计。

2. 工程优化设计和可视化定义

人们做任何事情都力求用最小的付出得到最佳的效果，这就是优化问题。机械、电气工程设计中，设计者更是希望寻求一组合理的设计参数，使由该组参数所确定的方案既满足各种设计的性能要求，又使其技术经济指标达到最佳，即实现了最优设计 [1] [2] [3] [4]。但常规的工程设计仍沿用着众所熟知的经验类比法；由于设计问题的复杂性及设计手段、方法的制约，不可能进行多方案的分析比较，更不可能得到最佳的设计方案。

工程优化设计即是将数学方法和计算机技术应用于工程项目或工业产品的最优设计方案的方法和技术。

工程的设计问题通常是相当复杂的，欲能利用计算机进行优化求解，必须对实际问题加以适当的抽象和简化，即建立便于求解的统一形式——数学模型。数学模型是进行优化设计的基础，根据设计问题的具体要求和条件建立完备的数学模型是优化设计成败的关键 [5] [6]。

俗话说“一图胜万语”，在科学研究、工程上有图则一目了然，无图搭配则如隔靴搔痒，很难窥得全貌。

MATLAB能够为广大科技工作中接受和喜爱的原因，除了其强大的计算功能外，就是它能够提供极其方便的绘图功能，也就是可视化功能。MATLAB的数据函数可视化可以方便地让用户从一堆杂乱无章的数据中观察数据间的内在关系，并进而获得数据背后隐藏的物理本质。MATLAB可以绘制多种类型的二维、三维图形，并可以进行动画演示；利用程序与绘图结合，可以将结果计算以图形显现，有助于了解计算过程以及分析计算结果，这在科学、工程中都非常重要 [7] - [12]。

3. 优化设计问题的可行域的可视化实现

一个可行的设计方案必须满足某些设计限制条件，这些限制条件被称作约束条件，也称为约束函数。凡满足所有约束条件的设计点，它在设计空间的活动范围即称为可行域。可行域也可看作满足所有约束条件的设计点的集合。

某优化问题，其优化数学模型为：

$\begin{array}{l}\min f\left(X\right)={\left(x_1-2\right)}^2+x_2^2\\ s.t.g_1\left(X\right)=-x_1+x_2-2\le 0\\ g_2\left(X\right)=x_1^2-x_2+1\le 0\\ g_3\left(X\right)=-x_1\le 0\\ g_4\left(X\right)=-x_2\le 0\end{array}$ (1)

式中：

x₁、x₂——设计变量；

$f\left(X\right)$ ——目标函数；

$g_1\left(X\right)$ 、 $g_2\left(X\right)$ 、 $g_3\left(X\right)$ 、 $g_4\left(X\right)$ ——约束函数；

$\min f\left(X\right)$ ——求解 $f\left(X\right)$ 的最优值；

s.t.——受约束于。

该优化问题的可行域并不能直接得到，可以借助MATLAB编程来达到目的。可行域即为红色曲线、绿色直线和垂直轴所包围的区域范围，如图1所示；图2所示为该优化问题可行域的三维表达。利用MATLAB优化求解得最优值为：X^* = [ 0.5536, 1.3064]^T，f(X^*) = 3.7989。

图中红色曲线代表g₂ (X)，绿色直线代表g₁ (X)

Figure 1. Plane visualization of feasible domain

图1. 可行域的平面可视化

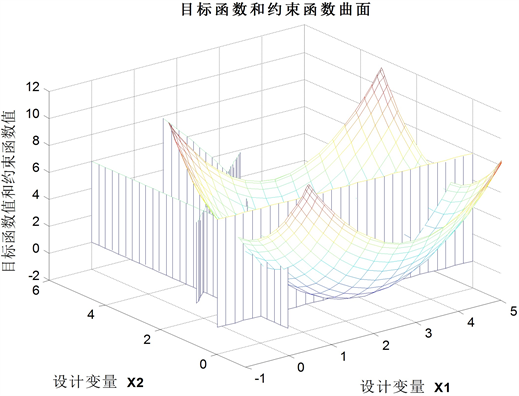
Figure 2. 3-D visualization of feasible domain

图2. 可行域的三维可视化

4. 一维优化设计问题的求解过程的可视化实现

MATLAB提供数据及函数的可视化技术，让离散、杂乱的数据以图形的方式，清晰地呈现在学习者和用户面前，便于观察、理解数据之间的扑朔迷离的内在关系。

一维优化问题是求解一元函数 $f\left(X\right)$ 的极小点和极小值的问题。一维优化问题是多维无约束和约束优化问题的基础；一维优化问题虽然只有一个设计变量，但是目标函数的性态有时特别复杂，很难判断最优解出现的区间，求解十分困难。目标函数的性态要满足“大—小—大”趋势，才能求解得到最优值。

在MATLAB软件环境下，只需较简单的操作就可以可视化呈现一维优化问题的求解过程。使用函数fminbnd即可完成该项任务，以优化问题： $f\left(X\right)=\sin \left(x\right)+3$ 为案例说明；图3为 $f\left(X\right)=\sin \left(x\right)+3$ 的变化趋势图，显然其优化值的区间在[4, 5]区间范围内；图4为fminbnd求解过程的进化过程。

Figure 3. Chart of changing trend of $f\left(X\right)=\sin \left(x\right)+3$

图3. $f\left(X\right)=\sin \left(x\right)+3$ 的变化趋势图

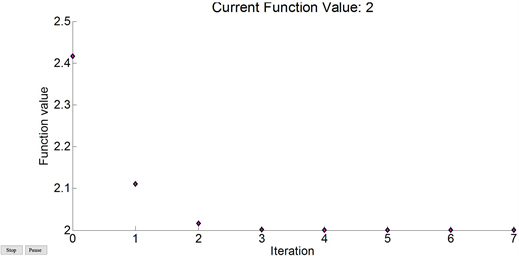
Figure 4. Evolution process of single-variable minimization

图4. 一维优化问题求解的进化过程

MATLAB程序实现如下：

%一维优化求解案例

%优化目标函数sin(x) + 3

figure (1)

x = [0:0.01:2]*pi; %变量x取值范围

y = sin(x) + 3; %优化问题的目标函数

plot(x, y) %变化趋势绘图

figure (2)

a = 3; %区间左端点的值

b = 5; %区间左端点的值

options = optimset('Display', 'iter', 'PlotFcns', 'optimplotfval')；

[x, fval] = fminbnd(@(x) sin(x) + 3, a, b, options) %一维优化问题求解

其它有代表性的一维优化问题的求解结论见表1。

Table 1. Conclusions for typical single-variable minimization

表1. 典型的一维优化问题的求解结论

5. 无约束优化设计问题的求解过程的可视化实现

优化问题的求解是针对复杂的数学极值问题提出的一种有别于数学解析法的数值解法，即不断地迭代循环、达到一定求解精度的解法。实际优化问题求解中，常常会利用检验函数来实现，如俗称的香蕉函数即是。

案例1：香蕉函数的数学表达式为：

$\min f\left(X\right)=100\ast {\left(x_2-x_1^2\right)}^2+{\left(1-x_1\right)}^2$ (2)

式中：

x₁、x₂——设计变量；

$f\left(X\right)$ ——目标函数；

$\min f\left(X\right)$ ——求解 $f\left(X\right)$ 的最优值。

香蕉函数的可视表现见图5所示。最优值为：X^* = [1.0000, 1.0000]^T，f(X^*) = 2.8336e−011。

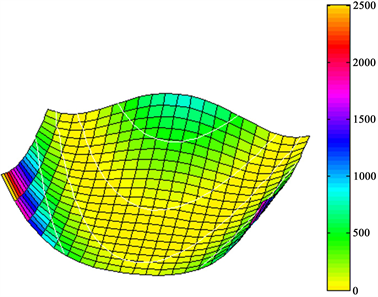
Figure 5. 3-Dvisualization of banana function

图5. 香蕉函数的三维可视表现图

MATLAB实现香蕉函数的可视表现的程序：

cla reset; %清除内存

axis off;

x = [−2:.2:2];

y = [−1:.2:3];

[xx, yy] = meshgrid(x, y);

zz = 100*(yy − xx.^2).^2 + (1 − xx).^2;%香蕉函数

hsv2 = hsv;

hsv3 = [hsv2(11:64, :); hsv2(1:10, :)];

surfHndl = surface(x, y, zz, 'EdgeColor', [.8 .8 .8]);%三维曲面图

axis off;

view(10, 55);

colormap(hsv3); %三维彩色图

hold on;

[c, contHndl] = contour3(x, y, zz + 50, [100 500], 'k');

set(contHndl, 'Color', [.8 .8 .8]);

drawnow

colorbar%色棒

其优化求解的过程可视化见图6所示。

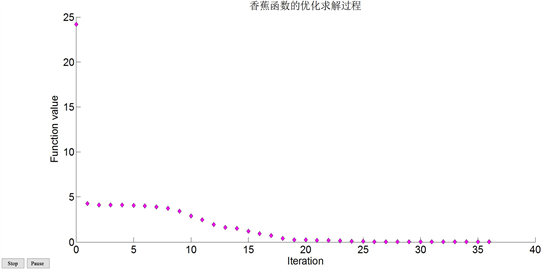
Figure 6. Visualization of optimization of banana function with unconstraint

图6. 香蕉函数无约束优化求解过程的可视表现

MATLAB优化求解香蕉函数程序：

%香蕉函数的无约束优化求解

clc; %清屏

banana = @(x)100*(x(2) − x(1)^2)^2 + (1 − x(1))^2;

options = optimset('LargeScale', 'off', 'Display', 'iter', 'PlotFcns', 'optimplotfval');

[x, fval] = fminunc(banana, [−1.2, 1], options)

案例2：复杂的无约束优化问题，其目标函数为：

$\min f\left(X\right)=x_1^3-x_2^3+3\ast x_1^2+3\ast x_2^2-9\ast x_1$ (3)

式中：

x₁、x₂——设计变量；

$f\left(X\right)$ ——目标函数；

$\min f\left(X\right)$ ——求解 $f\left(X\right)$ 的最优值。

案例2有4个驻点，给优化求解带来极大困难。在本例的优化求解过程中，只能采用试探法进行。对于具有多个局部优化解的问题求解是非常困难的，此时，借助可视化技术不适为一个可行的和高效的解决问题的手段(见表2和图7)。

MATLAB优化求解程序：

clc; %清屏

Suanli02 = @(x) x(1)^3 − x(2)^3 + 3*x(1)^2 + 3*x(2)^2 − 9*x(1);%定义函数句柄

[x, fval] = fminunc(suanli2, [0, 0]) %初始点值[0, 0]可改变，试探求解

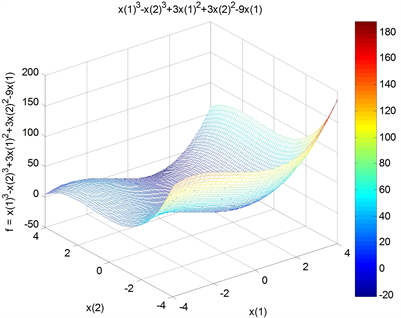(a) 案例2的3-D可视化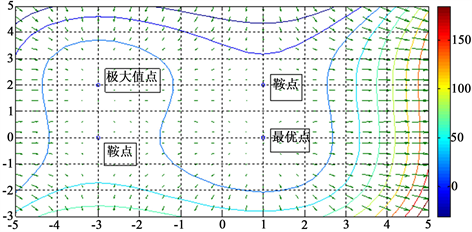(b) 案例2的等高线、梯度和极值点

Figure 7. Visualization of case 2

图7. 案例2的可视化表达

Table 2. Conclusions for optimization of case 2

表2. 算例2的优化结论

6. 约束优化设计问题的求解过程的可视化实现

当香蕉函数增加约束条件后，该优化问题就变为约束优化问题。

$\begin{array}{l}\min f\left(X\right)=100\ast {\left(x_2-x_1^2\right)}^2+{\left(1-x_1\right)}^2\\ s.t.x_1^2+x_2^2\le 1\end{array}$ (4)

式中：

x₁、x₂——设计变量；

$f\left(X\right)$ ——目标函数；

$\min f\left(X\right)$ ——求解 $f\left(X\right)$ 的最优值；

s.t.——受约束于。

约束优化问题的求解要困难一些，图8是香蕉函数的约束优化求解的可视化过程；其最优值为：X^* = [0.7864, 0.6177]^T，f(X^*) = 0.0457。

Figure 8. Visualization of optimization of banana function with constraint

图8. 香蕉函数约束优化求解过程的可视表现

%香蕉函数__约束优化求解

clc; %清屏

x0 = [0 0]; %初始点

banana = @(x)100*(x(2) − x(1)^2)^2 + (1 − x(1))^2;%定义香蕉函数

options = optimset('LargeScale', 'off', 'Display', 'iter', 'PlotFcns', 'optimplotfval');

[x, fval] = fmincon(banana, x0, [], [], [], [], [], [], @banana2, options)

function [c, ceq] = banana2(x) %约束条件的子程序

c = x(1).^2 + x(2).^2 − 1; %不等式约束条件

ceq = []; %等式约束条件，本例没有等式约束条件

工程应用案例：某箱型盖板的优化问题 [13] 是一个实际的工程问题，它追求箱型盖板的质量最轻。箱型盖板的问题如图9所示，其优化数学模型见式(5)。设计变量的选取：翼板厚度t_f为x₁，盖板高度h为x₂。

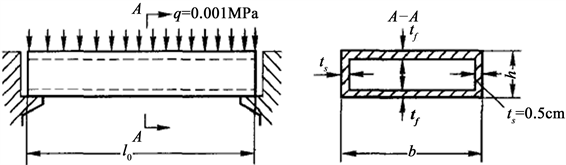
Figure 9. Schematic graph of box-type cover plate

图9. 箱型盖板示意图

$\begin{array}{l}\min f\left(X\right)=120x_1+x_2\\ s.t.g_1\left(X\right)=1-0.25x_2\le 0\\ g_2\left(X\right)=1-\frac{7}{45}{x}_1{x}_2\le 0\\ g_3\left(X\right)=1-\frac{7}{45}{x}_1^3{x}_2\le 0\\ g_4\left(X\right)=1-\frac{1}{320}{x}_1{x}_2^2\le 0\\ g_5\left(X\right)=-x_1\le 0\\ g_6\left(X\right)=-x_2\le 0\end{array}$ (5)

式中：

x₁、x₂——设计变量；

$f\left(X\right)$ ——目标函数；

$\min f\left(X\right)$ ——求解 $f\left(X\right)$ 的最优值；

$g_1\left(X\right)$ 、 $g_2\left(X\right)$ 、 $g_3\left(X\right)$ 、 $g_4\left(X\right)$ 、 $g_5\left(X\right)$ 、 $g_6\left(X\right)$ ——约束函数；

s.t.——受约束于。

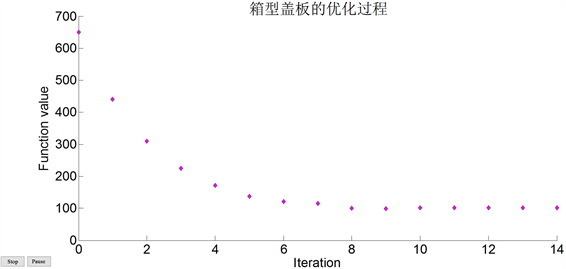
Figure 10. Visualization of optimization of box-type cover plate

图10. 箱型盖板优化求解过程的可视表现

图10为该工程问题的MATLAB优化求解的可视化过程。在MATLAB软件平台求解其最优值为：X^* = [0.6332, 25.3264]T，f(X^*) = 101.3056。

MATLAB求解程序：

clc;%清屏

x0 = [5, 50]; %箱形盖板优化问题的初始值

options = optimset('LargeScale', 'off', 'Display', 'iter', 'PlotFcns', 'optimplotfval');

[x, fval, exitflag, output] = fmincon(@xiangxingYH01, x0, [], [], [], [], [], [], @xiangxingYH02, options)

%目标函数子程序xiangxingYH01.m

function f = objfun(x)

f = 120*x(1) + x(2); %优化设计的目标函数

%约束函数子程序xiangxingYH02.m

function [c, ceq] = confun(x)

c = [1 − 0.25*x(2);

1 − (7/45)*x(1)*x(2);

1 − (7/45)*x(1)^3*x(2);

1 − (1/320)*x(1)*x(2)^2;

−x(1);

−x(2)];%不等式约束条件

ceq = [];%等式约束，[]表示无等式约束条件

7. 结论

工程优化设计问题的求解会遇到许多困难，第一步是要正确理解优化设计问题的数学模型；其次，借助MATLAB的强大可视化功能，对理解优化设计问题的可行域表达、一维优化问题求解、无约束优化求解和约束优化问题的求解极为实用；同时，对于具有多个局部优化解的工程优化问题求解是非常困难的，借助MATLAB可视化技术不适为一个可行的和高效的解决问题的手段。