一类火力打击掩蔽库战机问题的建模与仿真

Modeling and Simulation of a Class of Firepower Strike Masking Garage Fighter Problems

摘要: 机场掩蔽库作为空军基地重要防护设施，常被视为火力打击的重点目标。为提高作战效费比，探究杀伤型侵爆弹的杀伤效果，具有重要的现实意义。本文首先构建了战机平面化模型，基于多元函数极值理论，分析了掩蔽库战机毁伤效果，给出了最优的杀爆弹起爆攻击位置和瞄准角度，应用误差分析验证了模型的灵敏度。

Abstract: As an important protective facility for air bases, the airport shelter depot is often regarded as the key target of firepower strikes. In order to improve the combat effectiveness and cost-to-fee ratio, it is of great practical significance to explore the lethal effect of anti-personnel explosive bombs. In this paper, the flattening model of the fighter is constructed, based on the theory of multivariate function extremum, the damage effect of the masking library fighter is analyzed, the optimal detonation attack position and aiming angle of the anti-explosive bomb are given, and the sensitivity of the model is verified by application error analysis.>

1. 引言

将敌战机消灭于地面是打击敌方空中有生力量的最佳方式 [1]，在现代化高科技战场中，根据弹药的特性和飞机掩蔽库的结构特点，杀伤爆破型弹药(简称杀爆弹)以其释放高动能破片杀伤飞机掩蔽库中战机方式，凭借较大的杀伤面积在一定程度上抵消目指和命中误差带来的劣势，相比同类弹药更受各国青眛，在近两年地区局部战争中，交战双方利用携带杀爆弹的制导导弹打击对方空军基地的案例层出不穷。2022年2月，俄罗斯运用类似的携带杀爆弹精确制导导弹对乌克兰军用机场发动突袭行动，快速消灭了乌克兰空军有生力量。

杀爆弹应用研究更加受到各国各军兵种的高度重视，如何更有效的提高杀爆弹的杀伤效果。前人建立自然破片模型 [2] [3] [4] [5]，从杀爆弹的爆炸机理分析了如何增强破碎片侵彻毁伤效果，而且针对地面飞机的毁伤仿真 [1] [6] [7] 进行研究，从地面飞机毁伤特性分析入手，利用投影法在典型条件下对地面飞机进行了毁伤仿真计算，在此对于数值计算具有借鉴意义，另外单机掩蔽库的毁伤效果研究 [8] 也是层出不穷，主要从生存概率计算模型 [10] 和掩蔽库整体结构设计 [9] [11] 的角度去增强掩蔽库的综合防护能力 [12]，但针对用杀爆弹打击掩蔽库的战机的研究却很少。在兼顾杀爆弹的杀伤特点的同时，又要考虑到掩蔽库的保护作用，所以如何调整杀爆弹爆炸时角度让弹片发挥最大效能、最大限度的降低掩蔽库的综合防护能力、给掩蔽库中战机造成最大伤害有待研究。

文中以典型的战斗机为例，在给定的起爆高度下对“投影”后的飞机进行毁伤效果分析，建立飞机平面化模型和火力有效覆盖打击模型，通过给定的起爆高度先找到完全覆盖点和完全遮蔽点，通过在这两点范围建立多元函数 [4] 求出毁伤值。

2. 飞机毁伤效应数值计算模型

2.1. 侵爆弹爆炸模型

一般情况下，杀爆型弹道导弹爆炸杀伤范围按照炸点为起点呈圆锥形，射程250~500 km，圆概率偏差10 m，飞行速度4000 km/s，杀爆型弹道导弹以瞄准点为基准沿着弹道飞行，在距地面一定高度起爆，破片沿弹头在起爆点的飞行方向呈甜筒状高速均匀抛撒。可从掩蔽库前侧或后侧无遮挡处射入掩蔽库内部，在一定距离内可有效打击驻停飞机，但无法穿透掩蔽库钢混防护层，如图1。

Figure 1. Schematic diagram of the explosion of the invading bomb

图1. 侵爆弹爆炸示意图

2.2. 飞机掩蔽库模型

飞机掩蔽库简称机库，其结构形式一般是大跨度单层建筑物，往往由墙壁、棚顶和机库门构成，大部分机库承重体系为钢结构，依靠两边或三边墙面进行支撑，墙面有砖混或凝土材质，也有采用钢结构作为承重柱并覆以塑料作为外表面；顶部采用大跨度，钢结构梁或框架，覆以塑料作为棚顶；机库门按机库全高或飞机形状设计，分若干由薄钢板构成的门扇。张舵 [2] 等发现有些情况下，机场中会灵活、快速搭建临时的简易机库，用以满足各种任务需求。简易机库一般不需要机库门，只需要搭建承重的钢结构框架，覆以软质塑料或帆布。

建立飞机掩蔽库模型，飞机掩蔽库呈现半圆筒状，外半径长12.2 m，内半径10.2 m，宽度为22 m，高度为9 m，在飞机掩蔽库的内侧存在两个对称分布的加固物体；前后两端敞开，没有机库大门，模型如下图2、图3所示：

Figure 2. The mask library is facing the structure diagram

图2. 掩蔽库正对结构图

Figure 3. Mask the side structure of the library

图3. 掩蔽库侧面结构图

2.3. 飞机平面化模型

尽管飞机可以设计用于很多不同的目的，大多数还是有相同的主要结构。一般飞机实体图如图4所示，它的总体特性大部分由最初的设计目标确定。大部分飞机结构包含机身(fuselage)，机翼(wings)，尾翼(empennage)，起落架(landing gear)和动力装置(powerplant)以飞机的轮廓为基本组件，将飞机的轮廓线拟合成标准函数曲线，先建立了将飞机简化为三角形的模型，再设计了基于以机头为原点，飞机平面化后重要的七点(分别为侧翼前/中/后，机身，尾翼前/中/后)精确化飞机为分段函数，飞机平面化后忽略其体积对破片命中率的影响，将实验环境理想化不考虑破片是否有破坏以分析机库内部，和设施是否受到毁伤，以命中破片数衡量毁伤效果。

在之前所描述的基础上较为准确的得到飞机在俯视的角度下飞机的平面化模型，如图5所示。

Figure 4. General aircraft physical diagram

图4. 一般飞机实体图

Figure 5. Schematic diagram of the aircraft after flattening

图5. 飞机平面化后示意图

2.4. 基于飞机平面化火力有效覆盖打击模型

2.4.1. 模型说明

AB线段代表着飞机，掩蔽库高为h₁，侵爆弹在距离地面H的地方爆炸，E为遮挡点，首先假设杀爆弹正对中轴线瞄准，为保证侵爆弹爆炸之后产生的弹片能够到数量最多进入掩蔽库，在完全通视点和完全遮蔽点间寻找到最佳的爆炸点P。根据进入掩蔽库的弹片数量与弹片密度和弹片覆盖到飞机的面积与弹片总面积比，在此确定侵爆弹的爆炸点的爆炸范围，分别以机头和机尾同掩蔽库最高点E连接的两条直线相交于高为H平行于水平面的直线于C，D两点，C是完全通视点，D是完全遮挡点。CD线段就是侵爆弹的发射的范围，如下图6所示：

Figure 6. Schematic diagram of the model of the simulated strike aircraft shelter

图6. 仿真打击飞机掩蔽库模型示意图

已知条件各点坐标：A(a, h)，B(b, h)，C(c, H)，D(0, H)，E(e, h₁)；飞机函数g(x)；设爆炸点杀爆弹产生的弹片为N，弹片散角θ，F是最远打中点，最远打中点F至B点的距离为x；g'(x)表示覆盖面积S₁同FB之间的关系；总弹片投影面积S₂；投影飞机上的弹片面积S₁；散布面的投影比例尺k；弹片总投影半径r；

由此推出：

$x=\left(H-h\right)\tan \left(\theta +\alpha \right)-b+t$

进而通过投影飞机上的弹片面积S₁占总弹片投影面积S₂的比例求出击中飞机的弹片数W，从而建立目标函数：

$W=N\frac{k{S}_1}{S_2}=N\frac{g\left(x\right)\frac{\cos \left(\alpha +\theta \right)}{\cos \theta }}{\pi r^2}=\frac{N\cdot g\left[\left(H-h\right)\tan \left(\theta +\alpha \right)-b+t\right]{\cos }^2\left(\alpha +\theta \right)}{\pi {\left(H-h\right)}^2{\sin }^2\theta \cos \theta }$

令 $\tan \left(\theta +\alpha \right)=\beta$，通过恒等代换 [13] 得出：

$w\left(\beta ,t\right)=\frac{g\left[\left(H-h\right)\beta -b+t\right]}{{\left(1+{\beta }^2\right)}^{\frac{3}{2}}}$

2.4.2. 偏导函数w(β, t)求解

1) 确定变量β, t的取值范围

$\{\begin{array}{l}0<t<\frac{H-h_1}{h_1-h}\left(a-b\right)\\ \frac{b-t}{H-h}<\beta <\frac{e-t}{H-h_1}\end{array}$

得出t的取值范围：

$\{\begin{array}{l}t\le e-\left(H-h_1\right)\beta \\ b-\beta \left(H-h\right)\le t\end{array}$

定理：假设掩蔽库高为h₁，杀爆弹正对掩蔽库中轴线瞄准，水平移动范围X₁~X₂，且在距离地面H的地方爆炸，杀爆弹爆炸后产生的弹片为N，弹片散角θ。当爆炸点位置和瞄准角度满足 $t_{\max }=e-\left(H-h_1\right)\beta$，β取驻点值β = β₀时，击中飞机的弹片数W取最大值。

2) 对函数w(β, t)的变量分别求偏导：

通过分别对于变量β和t求偏导发现且w_t > 0，w_β存在未知函数难以判断(如下公式推导)无法利用多元函数求极值中的驻点，所以不能通过黑塞矩阵理论求极值，那么在这种情况下w_max在t的取值在端点，后将用β表示的t带回原公式形成单一β变量，在驻点值β = β₀时W取的最大值。

$w_t=\frac{g^{\prime }\left[\left(H-h\right)\beta -b+t\right]}{{\left(1+{\beta }^2\right)}^{\frac{3}{2}}}$

$w_{\beta }=\frac{\left(H-h\right)g^{\prime }\left[\left(H-h\right)\beta -b+t\right]{\left(1+{\beta }^2\right)}^{\frac{3}{2}}-3\beta {\left(1+{\beta }^2\right)}^{\frac{1}{2}}g\left[\left(H-h\right)\beta -b+t\right]}{{\left(1+{\beta }^2\right)}^3}$

首先对变量t求偏导 [14]：结果大于0；又由于g(x)是以飞机宽度为自变量的函数，所以g'(x)恒大于0将取 $t_{\text{max}}=e-\left(H-h_{\text{1}}\right)\beta$ 回代入原式得出：

$w_1\left(\beta \right)=\frac{g\left[\left(h_1-h\right)\beta +e-b\right]}{{\left(1+{\beta }^2\right)}^{\frac{3}{2}}}$

然后对β求偏导：求出驻点值β=β₀通过二阶求偏导导，确定

$w{\left(\beta ,t\right)}_{\max }=w_1(\; \beta \; 0\; )$

在代回原式验证 $t_{\max }=e-\left(H-h_1\right)\beta$ 仍然在t的取值范围之内：

最终得到结果：

$W=\frac{Nw{\left(\beta ,t\right)}_{\max }}{\pi {\left(H-h\right)}^2{\sin }^2\theta \cos \theta }$

推论：假设掩蔽库高为h₁，杀爆弹在距离地面H的平面内爆炸，杀爆弹爆炸后产生的弹片为N，弹片散角θ。当爆炸点位置和瞄准角度满足：爆炸点正对掩蔽库的中轴线线上 $t_{\max }=e-\left(H-h_1\right)\beta$，β取驻点值β = β₀时，击中飞机的弹片数W取最大值。

在高为H的水平面上建立以0为原点的坐标系X0Y'，C_o (c_o, 0)为C左边的一点c_o > 0, D_o (d_o, 0)为D右边一点D_o < 0, P_o (x_o, y_o)为平面上的任意一点且y_o不等于0；将平面分化为四个部分，分别为线段CD，射线DD_o, CC_o，点P_o所在域，如图7所示：

Figure 7. Schematic of the coordinate system x0y

图7. 坐标系x0y示意图

上文已经得出：

$W\left(x\right)=\frac{Nkg\left(x\right)}{\pi r^2}$

在CD上P点取最大值时W(x)满足条件 $w\left(\beta ,t_{\max }\right)=w_1\left({\beta }_0\right)$ 下面证明在β相同的情况下P仍然为平面的最优解，当y=0时，设w(x)为目标函数：

$W\left(x,y^{\prime }\right)=\frac{Nkg\left(x\right)}{\pi r^2}\left(y=0\right)$

由上述已知 $w\left(t_o,0\right)\ge w\left(x_{\text{1}},0\right)$，x₁取值范围[0, c]

1) 证明 $w\left(c,0\right)=w\left(c_o,0\right)$

因为C点为完全遮蔽点， $w\left(c_o,0\right)=w\left(c,0\right)=0$

2) 证明 $w\left(d_o,0\right)\le w\left(0,0\right)$

设D_o如图8所示：

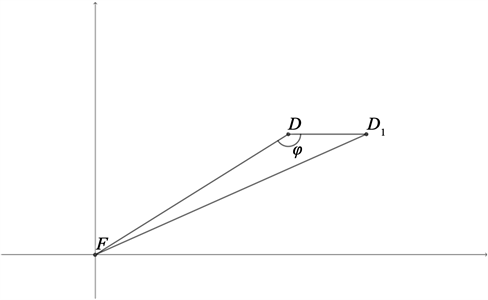
Figure 8. Schematic diagram of the location of the D_o-point

图8. D_o点方位示意图

可知在最远弹着点相同时，由于ψ > 90˚得出D_oF > DF；又因为r = DFtan(θ)所以r^o > r；从而得出 $w\left(d_o,0\right)<w\left(0,0\right)$。

3) 证明 $w\left(x_o,0\right)>w\left(x_o,y_o\right)$，

对原式进行求导比较大小

$w\left(x_o,y_o\right)=\frac{1}{{\left(1+\sin y_0^2\right)}^{\frac{3}{2}}}w\left(x_o,0\right)$

求导得到 $w{\left(x_o,y_o\right)}_{\max }=w\left(x_o,0\right)$

由此可知 $w\left(x_o,y_o\right)<w\left(x_o,0\right)$

综合上述三点：

$\begin{array}{l}w\left(t_o,0\right)\ge w\left(x_1,0\right)\\ w\left(t_o,0\right)\ge w\left(0,0\right)>w\left(d_o,0\right)\\ w\left(t_o,0\right)\ge w\left(c_1,0\right)=w\left(c_o,0\right)\end{array}$

得出P为CD所在直线的最优解，又因为 $w\left(t_o,0\right)>w\left(t_o,y_o\right)$ 最终得出P为所在高为H的水平面为最优解。

3. 三数值模拟

3.1. 案例

为了验证模型的科学性和实用性，选择掩蔽库遮蔽点E坐标h₁ = 9m侵爆弹爆炸点H = 20m，设爆炸点正对飞机掩蔽库正中央，忽略弹药实际落点偏移的影响，考虑爆炸弹爆炸后，破片的飞行方向是任意的，根据侵爆弹的爆炸方式，假设侵爆弹爆炸后破片沿弹头在起爆点的飞行方向呈甜筒状高速均匀抛撒，破片飞散角分别为45˚，破片数量分别为300片。

现以飞机的外围轮廓建立平面模型，并得出飞机的函数曲线，分别对飞机头部和尾部进行仿真计算。

3.2. 整体毁伤效果

将侵爆弹打击掩蔽库的事件看成平均概率事件，侵爆弹的打击效果以破片的打中数量表示，进而用蒙特卡诺算法通过面积比的方法求出击毁掩蔽库飞机的破片均值数量，最终通过确定事件得期望概率得到击毁飞机的侵爆弹数量，

对于飞机的头部平面化后，在不同爆炸点作用下的毁伤效果不尽相同，根据机头平面化并简化成一个三j角形到的模型函数曲线g(x) = Ax² (A = 0.852，x代表击中最远点到机头点的距离)根据推导公式w(t, β)，求出当W(β)取最大值时t = 4.188，回代w(t, β)，求出W(β) = 25片(根据取整原则)，表示的是远距离大起爆角，以提高飞机覆盖面积，最终求出最少需要T/25枚导弹才能达到预定打击效果(T表示达到摧毁效果所需命中单片数)。

对于飞机的尾部部平面化后得到的模型函数曲线

$g\left(x\right)=Bx-A{x}^2\left(A=0.852,B=5.14\right)$

根据推导公式w(t, β)，求出当W₁取最大值时t=17.5117，回代w(t, β)，求出W(β) = 175片(根据取整原则)表示的是近距离小起爆角，减小散步面积，最终求出侵爆弹n = [T/176] + 1枚导弹才能达到预定打击效果。

由于飞机的样式各异，用三角形替代会出现较大误差，现对平面飞机进行进一步处理，以飞机重要的四个部分机头，侧翼，机身，尾翼为主要参数输入构建飞机的精确分段模型，确立了以机头为原点的七点模型(图9)，重新计算打击效果。

Figure 9. Schematic of aircraft flattening

图9. 飞机平面化示意图

设输入横坐标为x(i) (i = 1 − 7)，纵坐标为y(i) (i = 1 − 7)，若x_i < x < x_i+1则：

$G\left(x\right)=\left({\displaystyle {\sum }_{k=0}^i\frac{\left(x\left(k\right)-x\left(k-1\right)\right)\ast \left(y\left(k\right)+y\left(k-1\right)\right)}{2}}\right)+y\left(k\right)\ast \left(x-x\left(k\right)\right)+\frac{2\ast \left(y\left(k+1\right)-y\left(k\right)\right)}{\left(x\left(k+1\right)-x\left(k\right)\right)\ast (x-x(\; k\; ))}$

于飞机头部，得出参数β = 1.947094，t = 5.040000，代入w(t, β)，求出W₁(β) = 47片，基于尾部得出参数β = 1.264457, t = 12.550000，代入w(t, β)，求出W(β) = 108片。在确定预期单片数T时分别得出所需T/47, T/108枚弹药。

3.3. 结果检验

针对上述的探究结果，利用灵敏度分析法对所设定的参数的精确度进行检验，以求证在所设定的参数范围内，实验结果的变化率在可控范围之内，下面分别对实验参数β, t, y₀在探究结果所得出的最佳值上下浮动5%，得出结果如表1所示：

Table 1. Parameter sensitivity analysis test

表1. 参数灵敏度分析检验

4. 小结

本文对掩蔽库中的飞机打击毁伤效果进行了数值计算研究，对比分析了杀爆弹不同起爆点及掩蔽库两端的毁伤结果，确定最佳爆炸点相对掩蔽库的位置，并与实例进行对比，得到结论如下。

1) 对于飞机尾部俯视面积较大的机型，应瞄准掩蔽库机尾出口进行打击的效果最好。

2) 杀爆弹对于机场掩蔽库内飞机的打击对于精度要求不高，性价比较高。

3) 在对表中相对变化值比较中可知beita在最佳值−5%和t在最佳值−5%时影响最大，而y0变化对结果影响较小，对此可以做进一步探究。

4.1. 模型评价

模型主要利用起爆点与飞机及掩蔽库的位置关系，巧妙地在一定范围内求出函数关系，进而转化为一个二元函数，并求解此局部最优解，通过证明得出此解为全局最优解。模型简单，计算速度快，可作为一个基础性的仿真，便于构建对于机场打击的混合策略。

4.2. 模型展望

对飞机进行毁伤评估，破片的命中数量不是唯一的评估标准，需要综合考量破片击中的位置、飞机大小和材质，还需要考虑破片是否有破坏以分析机库内部飞机和设施是否受到毁伤。另外，模型对于多弹型联合打击机场使用杀爆弹具有基础性参考。

NOTES

^*通讯作者。