基于多元线性回归的上证50股指追踪研究

Research on Tracking of Shanghai 50 Stock Index Based on Multiple Linear Regression

摘要: 指数追踪是指通过利用一个的股票组合复制某一现实指数或者虚拟指数的市场表现，由此来得到目标指数的市场表现，并尝试最小化跟踪误差。其目的是追踪一个股票指数的持仓及盈利表现。本文在追踪之前，对数据进行了回归诊断，诊断结果表明变量间存在多重共线性，逐步回归与岭回归方法能够很好的消除多重共线性。因此，本文主要采用了逐步回归与岭回归对上证50指数的5分钟K线数据进行指数追踪。指数追踪结果表明，利用逐步回归法对上证50指数的追踪效果优于岭回归法。

Abstract: Index tracking refers to using a stock portfolio to replicate the market performance of a real or virtual index to obtain the market performance of the target index and try to minimize tracking errors. Its purpose is to track the holdings and earnings performance of a stock index. Before tracking, this paper carried out regression diagnosis on the data. The diagnosis results showed that there was multicollinearity among the variables. Stepwise regression and ridge regression methods can eliminate multicollinearity very well. Therefore, this paper mainly uses stepwise regression and ridge regression to track the 5-minute K-line data of the Shanghai Stock Exchange 50 Index. The index tracking results show that the tracking effect of the SSE 50 index using the stepwise regression method is better than that of the ridge regression method.

1. 前言

指数追踪的目标是使得股票的投资者与股指期货空单对冲，由此来保值。指数型的基金管理者常常面临选择何种投资股票的问题，比较常用的有完全复制法和不完全复制法。其中，根据目标指数中每种成分股所占的权重来购买目标指数中的所有成分股，这种方法就叫做完全复制法。这种方法所需要的成本较高，在成分股较多的指数，比如沪深300这样的指数中并不适用。反之，购买目标指数中的部分股票的方法称为不完全复制法，然后最小化追踪组合收益率和目标指数收益率之间的误差获取资产比例，虽然存在一定的追踪误差，但是其投入的成本较低，更受投资者的青睐。

迄今为止，国内外学者们对指数追踪这一领域的研究还在持续不断的进行。Markowitz [1] 提出了投资组合理论(MPT)，Markowitz将复杂的投资组合选择问题巧妙的变成了一个被约束的二次规划问题，风险大小用方差来衡量，这一理论成为了现代投资组合理论的核心内容。许多学者在此基础上发展了一系列的指数追踪模型。Roll [2] 提出了基于均值–方差模型，期望收益不变，对 $\beta$ 进行约束，用最小化追踪误差的方差来进行建模。陈春锋和陈伟忠 [3] 对在此之前的指数追踪问题的研究方法、实证研究、研究模型等进行了深入的阐述。Walsh等 [4] 在追踪误差的理论下，对比不同的约束条件、不同的求解方法等对追踪误差的影响，以此来优化模型。刘磊 [5] 采用二进制和实数值混合编码的遗传BP网络对指数跟踪管理中的资金进行优化配置。获得较好的效果。倪禾 [6] 提出了一种基于启发式遗传算法的寻优方案，通过最大化效用函数来寻找一个最为经济的指数复制组合。倪苏云和吴冲锋 [7] 指出了线性跟踪误差最小化模型所具有的优点。Philippe Jorion [8] 探讨了受跟踪误差波动性(TEV)约束的活跃投资组合的风险和回报关系，也可以从风险价值角度来解释。杨虎，杨玥含 [9] 总结了多种多元回归方法在指数追踪中的应用。

股票市场中没有严格的函数关系，但很多变量之间是存在关联的，回归分析能够很好的刻画变量之间的相关关系。在设计阵病态或变量间存在多重共线性时，传统的回归模型不再适用，因为最小二乘估计本身设计的结构问题，当条件数过大时，均方误差也会迅速增大。当存在多重共线性时，有偏估计能够避免均方误差迅速增大的情况发生，所以本文选用经典的有偏估计模型，岭回归与逐步回归。

2. 模型介绍

2.1. 线性模型基本理论

一般的，设有p个解释变量 $X_1,X_2,\cdots ,X_p$，与被解释变量Y有如下关系：

$Y={\beta }_0+{\beta }_1{x}_1+\cdots +{\beta }_p{x}_p+\epsilon$ (1)

$\epsilon ~\left(0,{\sigma }^2\right)$ (2)

称(1)~(2)式为多元线性回归模型，线性函数

$f\left(x_1,x_2,\cdots ,x_k\right)={\beta }_0+{\beta }_1{x}_1+\cdots +{\beta }_k{x}_k$ (3)

称为多元线性回归函数， ${\beta }_i,i=0,1,\cdots ,p$ 称为回归系数。它们与 ${\sigma }^2$ 均未知。

设 $\left(x_{i1},x_{i2},\cdots ,x_{ip},y_i\right),i=0,1,\cdots ,n$ 为 $\left(X_1,X_2,\cdots ,X_p,Y\right)$ 的实验数据，且

$\{\begin{array}{l}{y}_i={\beta }_0+{\beta }_1{x}_{i1}+\cdots +{\beta }_p{x}_{ip}+{\epsilon }_i,i=1,2,\cdots ,n.\\ E{\epsilon }_i=0,\mathrm{var}{\epsilon }_i={\sigma }^2,i=1,2,\cdots ,n.\\ \mathrm{cov}\left({\epsilon }_i,{\epsilon }_j\right)=0,i\ne j;i,j=1,2,\cdots ,n.\end{array}$ (4)

记 $\beta ={\left({\beta }_0,{\beta }_1,\cdots ,{\beta }_p\right)}^{\prime },Y={\left(y_1,y_2,\cdots ,y_n\right)}^{\prime },\epsilon ={\left({\epsilon }_1,{\epsilon }_2,\cdots ,{\epsilon }_n\right)}^{\prime }$

$X=\left(\begin{array}{ccccc}1& x_{11}& x_{12}& \cdots & x_{1p}\\ 1& x_{21}& x_{22}& \cdots & x_{2p}\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ 1& x_{n1}& x_{n2}& \cdots & x_{np}\end{array}\right)$

则(4)式表示为：

$\{\begin{array}{l}Y=X\beta +\epsilon \\ E\epsilon =0,\mathrm{cov}\left(\epsilon \right)={\sigma }^2{I}_n\end{array}$ (5)

这就是通常所说的线性模型，它是统计学中极为重要的研究分支之一，式中X是一个纯量矩阵，称为设计矩阵或结构矩阵，在回归分析中一般假设X为列满秩，即 $rank\left(X\right)=p+1$ ； $E\epsilon =0$ 是n维零向量， $I_n$ 是n阶单位矩阵。

设 $\hat{\beta }={\left({\hat{\beta }}_0,{\hat{\beta }}_1,\cdots ,{\hat{\beta }}_p\right)}^{\prime }$ 是 $\beta$ 的估计量，则称

$\hat{y}={\left({\hat{\beta }}_0+{\hat{\beta }}_1{x}_1+\cdots +{\hat{\beta }}_p{x}_p\right)}^{\prime }.$ (6)

为线性回归方程。记

$\hat{y}={\left({\hat{\beta }}_0+{\hat{\beta }}_1{x}_{i1}+\cdots +{\hat{\beta }}_p{x}_{ip}\right)}^{\prime },i=1,2,\cdots ,n$ (7)

$\hat{Y}=X\hat{\beta }.$ (8)

残差平方和为

$\begin{array}{c}{S}_E^2=S_E^2\left(\hat{\beta }\right)={\displaystyle \underset{i=1}{\overset{n}{\sum }}{\left(y_i-{\hat{\beta }}_0-{\hat{\beta }}_1{x}_1-{\hat{\beta }}_2{x}_2-{\hat{\beta }}_3{x}_3-\cdots -{\hat{\beta }}_p{x}_p\right)}^2}\\ ={\Vert Y-X\hat{\beta }\Vert }^2=Y^{\prime }Y-2Y^{\prime }X\hat{\beta }+{\hat{\beta }}^{\prime }{X}^{\prime }X\hat{\beta }\end{array}$ (9)

对给定的观测数据 $\left(x_{i1},x_{i2},\cdots ,x_{ip},y_i\right),i=1,2,\cdots ,n$， $\hat{\beta }$ 其实就是下面最优化问题

$\underset{\beta }{\min }{S}_E^2\left(\beta \right)$ (10)

的最优解。因此 $\hat{\beta }$ 为

$\frac{\partial }{\partial \beta }{S}_E^2\left(\beta \right)=0$ (11)

的解。由(11)式可得

$X^{\prime }Y=X^{\prime }X\beta$ (12)

(12)式为正规方程。因为 $rank\left(X^{\prime }X\right)=rank\left(X\right)p+1$，所以 ${\left(X^{\prime }X\right)}^{-1}$ 存在，故得到 $\beta$ 得LS估计

$\hat{\beta }={\left(X^{\prime }X\right)}^{-1}{X}^{\prime }Y$ (13)

从而，(8)式为

$\hat{Y}=X\hat{\beta }=X{\left(X^{\prime }X\right)}^{-1}{X}^{\prime }Y$ (14)

需要注意的是(13)式具有两重性。

如果 $y_1,y_2,\cdots ,y_n$ 换成随机变量Y得一组随机样本 $Y_1,Y_2,\cdots ,Y_n$，则 $\hat{\beta }$ 是随机向量，为回归系数向量 $\hat{\beta }={\left({\beta }_0,{\beta }_1,\cdots ,{\beta }_p\right)}^{\prime }$ 的估计量；同样 $y_1,y_2,\cdots ,y_n$ 可以看成 $Y_1,Y_2,\cdots ,Y_n$ 的观测值，从而(13)式又是一个纯量向量，是回归系数向量的一个估计值。

2.2. 岭回归

岭回归实质上是一种改良的最小二乘估计法，岭回归放弃了最小二乘的无偏性，以损失部分信息、降低精度为代价获得的回归系数更为符合实际，更可靠的回归方法，对病态数据的拟合要强于最小二乘法。岭回归模型如下：

$\hat{\beta }\left(\lambda \right)={\left(X^{\text{T}}X+\lambda I\right)}^{-1}{X}^{\text{T}}y$

$\lambda$ 为岭系数，I为单位矩阵(对角线元素全为1，其他元素全为0)。岭回归的代价函数加入了一个正则项(如果没有正则项则是无偏估计)。下面是岭回归的代价函数：

$\begin{array}{l}J\left(\theta \right)=\frac{1}{2}{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\left(h_{\theta }\left(x_i\right)-y_i\right)}^2}+\lambda {\displaystyle \underset{i}{\overset{n}{\sum }}{\theta }_i^2}\\ J\left(\theta \right)=\frac{1}{2}{\left(X\theta -Y\right)}^{\text{T}}\left(X\theta -Y\right)+\lambda {\theta }^{\text{T}}\theta \\ =\frac{1}{2}\left({\theta }^{\text{T}}{X}^{\text{T}}X\theta -{\theta }^{\text{T}}{X}^{\text{T}}Y-Y^{\text{T}}X\theta +Y^{\text{T}}Y\right)+\lambda {\theta }^{\text{T}}\theta \\ \frac{\partial J\left(\theta \right)}{\partial \theta }=X^{\text{T}}X\theta -X^{\text{T}}Y+\lambda \theta \\ \theta ={\left(X^{T}X+\lambda I\right)}^{-1}{X}^{\text{T}}Y\end{array}$

其中， $\lambda \ge 0$，通过对 $\lambda$ 值的选择，可以减少多重共线性的影响，取不同的 $\lambda$ 值，可以得到不同的估计。当 $\lambda =0$， $\hat{\beta }\left(0\right)={\left(X^{\text{T}}X\right)}^{-1}{X}^{\prime }y$ 就是普通最小二乘估计。

2.3. 逐步回归

逐步回归的基本思想是将变量逐个引入模型，每引入一个解释变量后都要进行F检验，而后对以及选入逐步回归的变量进行逐个的检验，当后面选入的解释变量导致之前选入的解释变量不显著时将其剔除。由此可以保证每次引入新的解释变量，逐步回归方程里面的所有解释变量均显著。

有两种逐步回归的方法，一种是向前法：从模型中没有解释变量开始，反复添加最有帮助的解释变量，直到没有显著的预测变量选入回归方程。

首先，对p个自回归变量 $X_1,X_2,\cdots ,X_n$，分别对因变量Y建立一元回归模型

$Y={\beta }_0+{\beta }_i{X}_i+\epsilon ,i=1,2,\cdots ,p$

计算变量 $X_i$，并计算与之对应的回归系数的F检验统计量的值，记为 $F_1^{\left(1\right)},\cdots ,F_p^{\left(1\right)}$，取其中最大值 $F_{i1}^{\left(1\right)}$，即：

$F_{i1}^{\left(1\right)}=\max \left\{F_1^{\left(1\right)},\cdots ,F_p^{\left(1\right)}\right\}$

对给定的显著性水平 $\alpha$，记相应的临界值为 $F^{\left(1\right)}$， $F_{i1}^{\left(1\right)}\ge F^{\left(1\right)}$，则将 $X_{i1}$ 引入回归模型，记 $I_1$ 为选入变量指标的集合。

建立因变量Y与自变量子集 $\left\{X_{i1},X_1\right\},\cdots ,\left\{X_{i1},X_{i_1-1}\right\},\left\{X_{i1},X_{i_1+1}\right\},\cdots ,\left\{X_{i_1},X_p\right\}$ 的二元回归模型，共有 $p-1$ 个。计算变量的回归系数F检验的统计量，记为 $F_k^{\left(2\right)}\left(k\notin I_1\right)$，选其中最大值，对应自变量脚标记为 $i_2$，即：

$F_{i2}^{\left(1\right)}=\max \left\{F_1^{\left(2\right)},\cdots ,F_{i_1-1}^{\left(2\right)},F_{i_1+1}^{\left(2\right)},\cdots ,F_p^{\left(2\right)}\right\}$

对给定的显著性水平 $\alpha$，记相应的临界值为 $F^{\left(2\right)}$， $F_{i2}^{\left(1\right)}\ge F^{\left(2\right)}$ 则变量 $X_{i_2}$ 引入回归模型。否则，终止变量引入过程。后面重复上一步，直到没有变量通过F检验为止。

还有一种方法是向后选择法，从完整模型中的所有预测变量开始，以迭代方式删除贡献最小的预测变量，直到没有不显著的解释变量从回归方程删除。

3. 实证研究

3.1. 数据介绍

本文的数据来自于上证50指数及其成分股在2022年5月4日至2022年7月4日的5分钟K线收盘价数据，数据共2016条。其中，训练集占整个数据集的3/4，共计1344个数据，测试集占整个数据集的1/4，共计672个数据。

3.2. 回归诊断

在多元线性回归模型中，需要假定随机误差项 ${\epsilon }_i$ 服从 $N\left(0,{\sigma }^2\right)$。在目前的应用中，绝大多数都采用这样一些假设。如果分析表明实际问题不满足随机误差项的正态性假设，则可以对数据作适当的处理，使其满足或基本满足这些假设。

利用R语言获得上证50指数与其成分股之间的经验回归方程如下：

$\begin{array}{l}\hat{y}=-1.02X_1+5.93X_2-0.59X_3+4.41X_4+\cdots +1.93X_{14}+0.29X_{15}\\ +9.74X_{26}+0.27X_{27}+\cdots +9.45X_{43}+3.08X_{44}+\cdots +0.31X_{49}+0.63X_{50}\end{array}$

模型检验结果如表1所示：

Table 1. Least squares estimation model test

表1. 最小二乘估计模型检验

虽然模型通过检验，但拟合优度接近于1，存在过拟合现象；特征值最大为25.82，最小特征值为 0.0026。条件数大于1000，所以变量间存在复共线性。

结合图1初步分析得到该模型残差基本满足正态分布，但有多个异常值点。从QQ图来看基本满足正态性。

W正态性检验：H₀：残差服从正态分布。 $\omega =0.99831,P=0.2033$，由W检验结果知P值不显著，接受原假设，即残差满足正态性假设；图2图显示绝大部分点都在置信区间内，说明残差符合正态分布假设。

图3给出了前9个变量的偏残差图，表明变量间呈现线性关系。

3.3. 岭回归

考虑上证50指数与成分股之间关系的岭回归方程。首先选择岭参数，HBK、L-W给出的 $\lambda$ 值分别是0.0684、0.0092，GCV的最小值是0.0529，这里选择最小 $\lambda$ 值0.0092，得到岭回归方程为：

$\begin{array}{l}\hat{y}=112.42-0.88X_1+3.27X_2+0.08X_3+4.53X_4+\cdots +1.91X_{14}+0.29X_{15}\\ +9.75X_{26}+0.3X_{27}+\cdots +9.83X_{43}+3.53X_{44}+\cdots +0.33X_{49}+0.6X_{50}\end{array}$

将自变量的值带入岭回归方程中得到 $\hat{y}$ 的预测值，分析残差，以此求出普通残差。图4给出了岭回归方程的残差图，残差平方和为7083.679。

图4表明，岭回归方程刻画了上证50指数的趋势，但从方程的系数来看，负系数较少。理论上主成

Figure 1. Residual graph of SSE 50 index

图1. 上证50指数残差图

Figure 2. The QQ graph of the residual error of the Shanghai Stock Exchange 50 Index

图2. 上证50指数残差正太QQ图

Figure 3. SSE 50 Index Deviation Residual Graph

图3. 上证50指数偏残差图

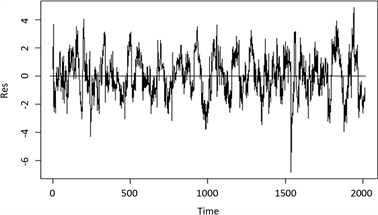
Figure 4. Residual plot of ridge regression equation

图4. 岭回归方程残差图

分估计和岭估计都能接近最小二乘估计的最佳残差，但主成分估计在应用中，会保留过多的主成分，会导致大量系数不显著，给进一步的分析带来困惑和隐患。

3.4. 逐步回归

通过逐步回归选择变量，第一步计算表明全部变量进行回归后 $\text{AIC}=-267.98$，有5个变量可供删除，删除后变量所能得到的最小值是 $\text{AIC}=-269.93$，对应删除的变量是 $X_{38}$ ；第二步发现有4个变量可供删除，最小AIC值是−271.80，需要删除的变量是 $X_{40}$，以此类推：

$\begin{array}{l}\hat{y}=114.1-6.5X_1+3.7X_2+5.49X_3+4.59X_4+\cdots +2.65X_{14}+0.25X_{15}\\ +5.87X_{26}+0.2X_{27}+\cdots +9.14X_{43}+2.14X_{44}+\cdots +0.07X_{49}+0.22X_{50}\end{array}$

模型平均残差平方和为38.25973，标准差为5.947346。

从图5中能够看到残差图显示是白噪声序列，且预测效果较好。

Figure 5. SSE 50 index tracking chart with stepwise regression method

图5. 逐步回归方法的上证50指数追踪图

4. 结论与展望

在多元线性回归中，变量间存在多重共线性是非常普遍的现象，对多重共线性程度的检测非常重要，这一定程度上决定了用何种方法去解决某一特定回归的复共线性问题。在本文中，多重共线性问题存在，但不算特别严重，所以本文用了两个比较经典的方法来对数据进行处理，分别是岭回归与逐步回归，这两个方法都能很好的解决多重共线性问题。另外，在指数追踪领域中，多元线性回归的应用较少。在本文的实证研究中，岭回归与逐步回归的残差平方和分别为7083.679与1912.9865。因此，在本文选用的上证50指数中，逐步回归法进行的追踪效果更优。相较于其他多元线性回归分析，逐步回归具备更合理的自变量筛选机制，能避免因无统计学意义的自变量对回归方程的影响。