用旋转矢量三维图理解拉普拉斯变换的物理意义

Understand the Physical Meaning of Laplace Transform with a 3D Map of Rotating Vectors

摘要: 拉普拉斯变换被广泛应用于不同的领域，但拉普拉斯变换的物理意义很少在信号和系统教科书中以图形方式描述。本文基于旋转矢量的三维图，提出拉普拉斯变换三维幅度谱和三维相位谱绘制方法。通过三维拉普拉斯变换谱描述拉普拉斯变换的本质上是将一个信号分解为无穷多广义非等幅振荡的正弦波线性组合。实验结果表明该方法能够直观揭示拉普拉斯变换复杂数学公式背后本质和物理含义。

Abstract: The Laplace transform is widely used in different fields, but the physical meaning of the Laplace transform is rarely graphically described in signal and systems textbooks. Three-dimensional amplitude spectrum and phase spectrum of the Laplace transform is proposed based on the three-dimensional graph of the rotation vector. The Laplace transform decomposes a signal into an infinite number of linear combinations of generalized variable amplitude sine waves. The experimental results show that the method intuitively reveals the essence and physical meaning behind the complex mathematical formula of Laplace transform.

1. 引言

拉普拉斯变换是一种有用的数学工具 [1] [2] [3]。拉普拉斯变换推导过程通常是将无法进行傅里叶变换的信号f(t)乘以一个指数衰减因子，然后再进行傅里叶变换，这种讲述方式是把拉普拉斯变换看作一个权宜的数学工具而使用，忽略了拉普拉斯变换的本质物理含义及其在信号处理中的价值。这会让初学者很难直观理解拉普拉斯变换的基本原理。本文从另一个角度来看待拉普拉斯变换，即指数衰减因子不是作为权宜手段而引入到信号的傅里叶分解中，而是认为指数衰减因子本身就是拉普拉斯信号分解的固有成分。信号的傅里叶频谱图相对容易绘制，然而拉普拉斯变换的幅度频谱和相位频谱是随实部σ和虚部ω变化的三维频谱，其频谱图的绘图非常困难，因而很难在相关教材中见到。本文从旋转矢量的角度出发，用三维图解方式给出拉普拉变换的具体过程，从而全面揭示拉普拉斯变换的物理含义。

2. 旋转矢量e^jωt物理意义与三维图

旋转矢量法是非常重要的矢量分析方法，在电磁场，交流电，稳态电路中都有重要的应用。最基本的旋转矢量如图1所示，复平面z = x + jy上有一个单位圆。单位圆上点P到圆心的连线与实轴的夹角为θ，P点运动轨迹z = e^jθ = cosθ + jsinθ。如果P点沿着单位圆逆时针以ω(ω > 0)的角速度运动，相位角θ = ωt，P点的复数形式为z = e^jωt。e^jωt对时间t作图，得到如图1(a)所示的三维螺旋线，时间t轴垂直于复平面。这里需要注意的是旋转矢量点的运动轨迹始终没有离开z平面，由于另一个轴是时间轴，所以会形成三维螺旋线。旋转矢量e^jωt分别在z平面、x-t平面、y-t平面投影为单位圆、cosωt、sinωt，三者相互垂直，如图1(b)所示。由于e^jωt是cosωt和sinωt的合成，因而e^jωt被称为等幅振荡的正弦波。为讨论方便将旋转矢量点所在的运动平面称为“z平面”，以区别于后文将要提到的复频率“s平面”。

(a) (b)

Figure 1. 3D map of rotation vector e^jωt

图1. 旋转矢量e^jωt的三维图

3. 复指数e^st的物理意义与三维图

将纯虚数频率jω扩展为复频率s = σ + jω，则e^jωt扩展成e^st。由于e^st = e^{σ + jωt}，其中e^σt是振幅，振幅按照指数规律随着时间变化。如图2所示是复指数信号e^st的三维图形及其投影图。当σ < 0，振幅随着时间t增长衰减到零。当σ = 0，e^st振幅是等幅振荡的。当σ > 0时，e^st振幅逐渐放大直至发散。

(a) σ < 0 (b) σ = 0 (c) σ > 0

Figure 2. 3D plot and projection plot of complex exponential e^st rotation vector

图2. 复指数e^st旋转矢量的三维图和投影图

图2所对应的波形都是在ω > 0的前提下分别考虑σ > 0，σ = 0和σ < 0三种情况所做出的图形。这个过程可以进一步扩展，继续考虑ω = 0和ω < 0的情况，这样将涵盖所有复平面所对应的时域波形。以复平面s作为底面，将不同复频率所对应的复指数信号e^st，画在对应复频率点上，每个波都是以z平面为底面，时间轴向上而形成的波形，如图3所示。

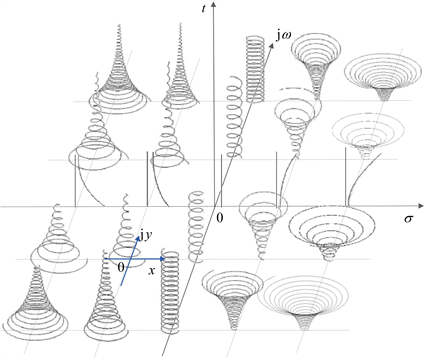
Figure 3. The waveform corresponding to each point of the complex frequency plane

图3. 复频率平面各点所对应的波形

不同复频率位置对应的波形特点如下：1) 在原点s = 0，即σ = 0，ω = 0，此时e^st = e^0t = 1，波形是恒定直流；2) 实轴右侧e^st = e^σt，由于σ > 0，ω = 0，因而波形是没有振荡的发散的指数函数，越像右越发散；3) 实轴左侧e^st = e^σt，由于σ < 0，ω = 0，因而波形是没有振荡的收敛的指数函数，越向左收敛越快；4) 在虚轴正向方向上，由于σ = 0，ω > 0，因而振幅不变，旋转矢量正向逆时针旋转。随着ω的增大旋转越来越快；5) 在虚轴负方向上，由于σ = 0，ω < 0，因而振幅不变，旋转矢量反向顺时针旋转，随着|ω|的增加，旋转越来越快；6) 在第1象限内σ > 0，ω > 0，波形正向逆时针旋转，振幅是发散的。横向方向上，ω不变，越向右，σ越大，越发散，形成的喇叭口越大。在纵向上，σ保持不变，随着ω的增加，旋转越来越快；7) 第2象限其与第1象限的区别在于所有的波形都是衰减的；8) 第3，4象限，所有的波形的旋转方向都与第2，1象限相反。

图3中以第3象限的某一波形为例，加了坐标轴xoy，表明旋转矢量点运动的轨迹，并非是从s平面对应的点开始运动，其真实的运动点始终绕着自身所在的z平面的原点旋转，注意z平面和s平面的区别。每个复频率点对应波形的矢量投影图如图4所示。从图4可见波形呈现各种形状有的类似旋风状，有的成直线与曲线等。

Figure 4. The projection of the waveform corresponding to each point in the complex plane

图4. 复平面各点所对应的波形的投影

4. 拉普拉斯变换的物理意义

仿照傅里叶变换的做法，可以导出拉普拉斯变换。傅里叶变换的物理含义是将信号分解为等幅振荡的正弦波e^jωt，拉普拉斯变换的物理含义是将信号分解为非等幅振荡的复指数信号e^st，无穷多非等幅振动合成时域信号，如公式(1)所示。

$f\left(t\right)=\frac{1}{2\text{πj}}{\displaystyle {\int }_{\sigma -j\infty }^{\sigma +j\infty }F\left(s\right){\text{e}}^{st}}\text{d}s$ (1)

被分解的正弦波微元为 $\left[\frac{1}{2\text{πj}}F\left(s\right)ds\right]{\text{e}}^{st}$，其复频率为s，复振幅为 $\frac{1}{2\text{πj}}F\left(s\right)ds$，复振幅中包含了幅度

和初相位，对于拉普拉斯变换的公式中频谱一定要注意实部σ为常数，这就意味着，这些小的正弦波微元只是对应着与jω轴平行的直线上的波。即图4中只是被虚线框选的那条直线上的波。如果σ = 0，波

的叠加只是虚轴上对应的波形，即傅里叶变换。以阶跃信号 $f\left(t\right)=u\left(t\right)$ 为例，其拉普拉斯变换为 $F\left(s\right)=\frac{1}{s}$，其幅度谱为 $\left|F\left(s\right)\right|$，相频为 $\phi \left(s\right)$，如图5所示。

(a) $\left|F\left(s\right)\right|$ 幅度频谱图 (b) $\phi \left(s\right)$ 相频谱图

Figure 5. Spectrogram of Laplace transform

图5. 拉普拉斯变换的频谱图

图5(a)是是幅度频谱图 $\left|F\left(s\right)\right|$，(b)是 $\phi \left(s\right)$ 相频谱图。图5(a)中，平面σ = σ₀是与实轴垂直的一个截面，该截面与 $\left|F\left(s\right)\right|$ 所形成的三维曲面相交，其交线A就是在σ = σ₀时的幅度频谱曲线，由于此时σ是常数，该曲线仅是jω的函数。移动平面σ = σ₀，让其趋向于原点，在移动过程中，A的最高值不断变大，到达原点时过度到无穷大。此时σ = 0，所形成的曲线为A₀，这正是傅里叶变换的频谱图。从中再次看到傅里叶变换是拉普拉斯变换的一个特例。同理，在图5(b)中，平面σ = σ₀与 $\phi \left(s\right)$ 曲面的交线B是在σ = σ₀的相频曲线，该曲线也只是jω的函数。若将平面σ = σ₀移动到原点，形成的曲线B₀正是傅里叶变换的相频谱图。移动过程中，平滑曲线B逐步过渡为有直角的折线。

5. 结语

针对复指数信号e^jωt和变幅振荡复指数信号e^st在直角坐标系下随时间变化的波形在一般的教材中较少讨论，本文用旋转矢量的图解法全面展示了等幅、变幅正弦波和直流、实指数信号，绘制了典型信号的三维图形及其平面投影图形，揭示出了这些信号的内在联系。通过三维频谱图可以全面分析拉普拉斯变换的物理含义。拉普拉斯变换的本质是将信号分解为无穷多非等幅震荡的正弦波线性组合。三维频谱图实验结果表明可以看出傅里叶频谱图是拉普拉斯在jw轴上频谱图的一个截面，拉普拉斯变换可以看作信号在复平面的分解，而傅里叶变换是信号的频域分解。

NOTES

^*通讯作者。