脉冲控制场下量子系统时变目标函数的有限时间跟踪控制

Finite-Time Time-Varying Target Function Tracking Control of Quantum Systems with Impulsive Control Fields

摘要: 研究一类脉冲控制场作用下封闭量子系统的有限时间跟踪问题。其目的是使量子系统的状态进入有界时变目标函数的轨迹。根据Lyapunov稳定性定理，设计改进的脉冲跟踪控制律，使得误差动态系统在有限时间内收敛到0。而有限时间跟踪意味着最优的收敛时间和更好的抗干扰能力。数值仿真验证了控制律在系统轨迹跟踪上的优越性。

Abstract: In this paper, a class of finite-time tracking issues for closed quantum systems under the action of impulsive control fields is addressed. The objective is to steer the state of quantum system into the trajectory of bounded time-variant target function. By using the Lyapunov stability theorem, modi-fied impulse tracking controllers are designed such that the error dynamical system convergence to zero in a finite time. While finite-time tracking means the optimality in convergence time and has better disturbance rejection. Numerical simulations are given to illustrate the effects of system’s trajectory tracking, and also given to demonstrate the superiority of the control laws which are proposed.

1. 引言

近年来，量子系统的控制问题由于其在量子通信 [1]，量子计算 [2]，量子信息 [3] 以及其它众多量子技术领域中的广泛应用，得到了深入的研究。经典控制理论中的多种方法 [4] [5] 被引入用于处理微观系统的控制问题。目前，Lyapunov控制理论 [6] [7] 已经成为设计量子系统控制器的一种有效方法。

目前，量子控制的研究主要分为量子系统的调控 [8] [9] 和跟踪 [10] [11]。前者在本征态、叠加态和混合态的调控及其收敛性分析上受到了广泛地关注和研究。后者研究轨迹跟踪，主要涉及任意时变函数的跟踪 [11] 和自由演化量子系统的跟踪 [12]。对于动态目标函数的量子态跟踪问题， [10] [11] 研究了一些典型目标函数，如斜坡函数和指数函数的跟踪。本文拟研究一类系统的量子态输出到目标函数的跟踪问题，其目标轨迹为有界时变函数。

为了在量子控制系统中实现更快的状态转移，可以考虑使用有限时间控制 [13] 技术这一高效的方法。据笔者所知，对于目标函数为有界函数的量子系统，其脉冲控制场下有限时间跟踪控制的研究至今鲜见于相关文献。量子系统对动态目标函数的有限时间跟踪控制是封闭量子系统状态转移研究中的一个重要环节，是一个值得讨论的课题。

2. 系统模型描述

考虑一类脉冲控制场作用下的Hilbert空间上的n-级封闭量子系统：

$i\hslash |\stackrel{\dot{}}{\psi }\left(t\right)\rangle =H|\psi \left(t\right)\rangle +{\displaystyle \underset{k=1}{\overset{\infty }{\sum }}\phi \left(\tilde{u}\left(t\right)\tilde{H}|\psi \left(t\right)\rangle \right)\delta \left(t-{\tau }_k\right)}$， (1)

其中 $|\psi \left(t\right)\rangle$ 是封闭量子系统的状态，且满足 $|\psi \left(t\right)\rangle ={\displaystyle \underset{i=1}{\overset{n}{\sum }}{c}_i|{\lambda }_i\rangle },i=1,2,\cdots ,n$。 $|{\lambda }_i\rangle$ 表示第i个本征态，而 $c_i,i=1,2,\cdots ,n$ 为复数，且满足 ${\displaystyle \underset{i=1}{\overset{n}{\sum }}{c}_i^2}=1$。

系统初始状态为 $\psi \left(0\right)={\psi }_0$。 $H=H_0+u_1\left(t\right)H_1+u_2\left(t\right)H_2$, $H_0$ 为系统自由Hermitian量， $H_1$ 和 $H_2$ 为控制Hamiltonian量，它们均为 $n\times n$ Hermitian矩阵，且假设均独立于时间。 $u_1\left(t\right)$ 和 $u_2\left(t\right)$ 为含时间的系统外加控制场。 $\phi \left(\tilde{u}\left(t\right)\tilde{H}|\psi \left(t\right)\rangle \right)$ 为非线性脉冲控制场，非线性项满足以下假设： $\phi \left(s\right)\le ls$。

$\tilde{H}$ 为脉冲控制Hamiltonian量。为了方便分析和计算，约化Planck 常数可取为 $\hslash =1$。

考虑到Dirac函数的性质，非线性脉冲控制场下的封闭量子系统也可写为以下形式：

$\{\begin{array}{l}i|\stackrel{\dot{}}{\psi }\left(t\right)\rangle =H|\psi \left(t\right)\rangle ,t\ne {\tau }_k\\ \Delta |\psi \left(t\right)\rangle =\phi \left(\tilde{u}\left(t\right)\tilde{H}|\psi \left({\tau }_k^{-}\right)\rangle \right),t={\tau }_k\end{array}$， (2)

在封闭量子系统中，系统输出函数 $y\left(t\right)$ 可表示为

$y\left(t\right)=\langle \psi \left(t\right)|P|\psi \left(t\right)\rangle$。 (3)

换言之，系统输出函数表示观测量P的期望值，其中P为Hermitian算符。可观测量可以表示为

$P={\displaystyle \underset{i=1}{\overset{n}{\sum }}{p}_i}|{\lambda }_i\rangle \langle {\lambda }_i|$， (4)

其中 $p_i$ 为P的投影，满足 ${\displaystyle \underset{i=1}{\overset{n}{\sum }}{p}_i}=1$。 $|{\lambda }_i\rangle$ 表示自由Hamiltonian量 $H_0$ 的第i个本征态。 $p_i$ 的取值决定系统对本征态 $|{\lambda }_i\rangle$ 的观测概率。P的不同取值可使系统有不同的测量输出。

因而， $y\left(t\right)=\langle c,Pc\rangle$，即

$y\left(t\right)=\left[\begin{array}{ccc}{c}_1& \cdots & c_n\end{array}\right]\left[\begin{array}{ccc}{p}_1& \cdots & 0\\ ⋮& \ddots & ⋮\\ 0& \cdots & p_n\end{array}\right]\left[\begin{array}{c}{c}_1\\ ⋮\\ c_n\end{array}\right]$。

进一步，系统输出可表示为

$y\left(t\right)={\displaystyle \underset{i=1}{\overset{n}{\sum }}{p}_i{c}_i^2}$。

显然， $0\le y\left(t\right)\le 1$。

本文主要研究在非线性脉冲控制场下封闭量子系统纯态轨迹的有限时间跟踪。

事实上，期望目标系统可以表示为随时间变化的函数。由于有界函数在工程中被广泛应用于控制系统的测试，考虑反正切函数作为目标函数，即

$s\left(t\right)=\arctan \left(\omega t+b\right)$。 (5)

此时，控制系统的跟踪控制问题及其控制任务的目标为：希望通过设计控制律使被控系统的输出 $y\left(t\right)$ 能够跟踪上目标系统的输出 $s\left(t\right)$，在有限时间内达到 $y\left(t\right)=s\left(t\right)=1$，完成跟踪。

控制系统跟踪的性能指标可定义为目标系统输出 $s\left(t\right)$ 和系统输出 $y\left(t\right)$ 的差值，即跟踪误差可表示为

$e\left(t\right)=s\left(t\right)-y\left(t\right)$。(6)

于是，由(2)~(6)可得系统跟踪误差为：

$\{\begin{array}{l}e\left(t\right)=\arctan \left(\omega t+b\right)-\langle \psi \left(t\right)|P|\psi \left(t\right)\rangle ,t\ne {\tau }_k\\ \Delta e\left(t\right)=\langle \phi \left(\tilde{u}\left(t\right)\tilde{H}|\psi \left({\tau }_k^{-}\right)\rangle \right),P\phi \left(\tilde{u}\left(t\right)\tilde{H}|\psi \left({\tau }_k^{-}\right)\rangle \right)\rangle ,t={\tau }_k\end{array}$。 (7)

为了能够获得本文的主要结论，这里引入以下引理。

引理1 [13] 假设 $V\left(t\right)$ 连续的正定函数，且满足以下不等式：

$\stackrel{\dot{}}{V}\left(t\right)\le -\rho V^{\alpha }\left(t\right),\forall t\ge t_0,V\left(t_0\right)\ge 0$

其中 $\rho >0$, $0<\alpha <1$ 为两个常数。于是，对于任意给定的 $t_0$， $V\left(t\right)$ 满足以下不等式：

$V^{1-\alpha }\left(t\right)\le V^{1-\alpha }\left(t_0\right)-\rho \left(1-\alpha \right)\left(t-t_0\right),t_0\le t\le t_1$，

而 $V\left(t\right)=0,\forall t\ge t_1$，其中 $t_1$ 由下式给定：

$t_1=t_0+\frac{V^{1-\alpha }\left(t_0\right)}{\rho \left(1-\alpha \right)}$。

引理2 [13] (Jesen不等式) 若 $a_1,a_2,\cdots ,a_n$ 为正数，且 $0<p<q$，则

${\left({\displaystyle \underset{i=1}{\overset{n}{\sum }}{a}_i^q}\right)}^{\frac{1}{q}}\le {\left({\displaystyle \underset{i=1}{\overset{n}{\sum }}{a}_i^p}\right)}^{\frac{1}{p}}$。

3. 跟踪控制律的设计

下面，利用Lyapunov方法设计有限时间跟踪控制律，使得误差控制系统在有限时间内收敛到0。

定理1考虑跟踪控制律(12)、(14)和(20)，则跟踪误差系统(7)在有限时间 $t_0=\frac{V^{1-0.5\left(1+\beta \right)}\left(0\right)}{2{\gamma }_0\left(1-0.5\left(1+\beta \right)\right)}$ 内稳定，并快速收敛到0，其中 $V\left(0\right)=\frac{1}{2}{e}^2\left(0\right)$。

证明：对于跟踪误差系统(7)，为了研究其有限时间收敛问题，考虑以下Lyapunov函数

$V\left(t\right)=\frac{1}{2}{e}^2\left(t\right)$。 (8)

当 $t\ne {\tau }_k$ 时，针对系统(7)，其Laypunov函数(8)对时间的一阶导数为

$\begin{array}{c}\stackrel{\dot{}}{V}\left(t\right)=e\left(t\right)\stackrel{\dot{}}{e}\left(t\right)\\ =e\left(t\right)\left(\frac{\omega }{1+{\left(\omega t+b\right)}^2}-\langle \psi \left(t\right)|i\left[H,P\right]|\psi \left(t\right)\rangle \right)\\ =e\left(t\right)(\frac{\omega }{1+{\left(\omega t+b\right)}^2}-2\mathrm{Im}\left(\langle \psi \left(t\right)|P{H}_0|\psi \left(t\right)\rangle \right)-2u_1\left(t\right)\mathrm{Im}\left(\langle \psi \left(t\right)|P{H}_1|\psi \left(t\right)\rangle \right)\\ -2u_2\left(t\right)\mathrm{Im}\left(\langle \psi \left(t\right)|P{H}_2|\psi \left(t\right)\rangle \right))\end{array}$ (9)

记 $I_0=\frac{\omega }{1+{\left(\omega t+b\right)}^2}-2\mathrm{Im}\left(\langle \psi \left(t\right)|P{H}_0|\psi \left(t\right)\rangle \right)$， $I_1=\mathrm{Im}\left(\langle \psi \left(t\right)|P{H}_1|\psi \left(t\right)\rangle \right)$， $I_2=\mathrm{Im}\left(\langle \psi \left(t\right)|P{H}_2|\psi \left(t\right)\rangle \right)$。

于是，(9)式可写成以下形式：

$\stackrel{\dot{}}{V}\left(t\right)=e\left(t\right)\left(I_0-2u_1\left(t\right)I_1-2u_2\left(t\right)I_2\right)$。 (10)

首先，通过设计 $u_1\left(t\right)$ 控制 $I_0$。可令

$I_0-2u_1\left(t\right)I_1=0$。 (11)

于是，可得控制律 $u_1\left(t\right)$ 为

$u_1\left(t\right)=\frac{I_0}{2I_1}$。 (12)

其次，为了使(9)负定，可令

$-2e\left(t\right)u_2\left(t\right)I_2\le 0$，

则取控制律 $u_2\left(t\right)$ 为

$u_2\left(t\right)=\gamma e\left(t\right)I_2$， (13)

其中待定常数 $\gamma >0$ 为控制增益。

为了使误差动态系统达到有限时间稳定，可进一步将控制律 $u_2\left(t\right)$ 改进为以下形式：

$u_2\left(t\right)=\gamma \mathrm{sign}\left(e\left(t\right)I_2\right){\left|e\left(t\right)I_2\right|}^{\beta }$， (14)

其中 $\gamma$ 为可调正常数，实常数 $\beta$ 满足 $0<\beta <1$。

注1：对于控制律的设计而言， $u_1\left(t\right)$ 的作用是用来消除漂移项 $I_0$，误差系统的有限时间收敛完全由 $u_2\left(t\right)$ 来控制。但是，由于跟踪控制律 $u_1\left(t\right)$ 为分式，其分母随系统状态变化可能为0，导致控制律为无穷大出现奇异点。为此，我们给出了两个改进的跟踪控制律，可消除或避免奇异性给跟踪控制带来的一些困难。为了解决这个问题，在实际应用时，可以进一步修正控制律 $u_1\left(t\right)$ 和 $u_2\left(t\right)$。改进的跟踪控制律可

以写成以下形式： $u_1\left(t\right)=\frac{I_0}{2I_1+{\epsilon }_1}$ 和 $u_2\left(t\right)=\gamma \mathrm{sign}\left(e\left(t\right)\left(I_2+{\epsilon }_2\right)\right){\left|e\left(t\right)\left(I_2+{\epsilon }_2\right)\right|}^{\beta }$，其中 ${\epsilon }_1$ 和 ${\epsilon }_2$ 为两个接近

于0的微小常数。

因此，考虑跟踪控制律(13)和 (14)，则(10)可得

$\stackrel{\dot{}}{V}\left(t\right)=-2e\left(t\right)I_2\left(\gamma \mathrm{sign}\left(e\left(t\right)I_2\right){\left|e\left(t\right)I_2\right|}^{\beta }\right)\le -2\gamma {\left|e\left(t\right)\right|}^{\beta +1}$， (15)

利用引理2，可得

${\left({\left|e\left(t\right)\right|}^{\beta +1}\right)}^{\frac{1}{\beta +1}}\ge {\left({\left|e\left(t\right)\right|}^2\right)}^{\frac{1}{2}}$。

因此，

${\left|e\left(t\right)\right|}^{\beta +1}\ge {\left(e^2\left(t\right)\right)}^{\frac{\beta +1}{2}}$。 (16)

将(16)代入(15)，于是，

$\stackrel{\dot{}}{V}\left(t\right)\le -2\gamma {\left(e^2\left(t\right)\right)}^{\frac{\beta +1}{2}}=-2\gamma {\left(\frac{1}{2}\right)}^{-\frac{\beta +1}{2}}{\left(\frac{1}{2}{e}^2\left(t\right)\right)}^{\frac{\beta +1}{2}}=-{\gamma }_1{V}^{\frac{\beta +1}{2}}\left(t\right)$，

其中 ${\gamma }_1=2^{\frac{\beta +3}{2}}\gamma$。

当 $t={\tau }_k$ 时，由于系统状态 $|\psi \left(t\right)\rangle$ 在脉冲位置右连续，于是可得

$\begin{array}{c}V\left({\tau }_k,e\left({\tau }_k\right)\right)=V\left({\tau }_k^{+},e\left({\tau }_k^{+}\right)\right)\\ =\frac{1}{2}{\left(e\left({\tau }_k^{-}\right)+\Delta e\left({\tau }_k^{+}\right)\right)}^2\\ =\frac{1}{2}{\left(e\left({\tau }_k^{-}\right)+\langle \phi \left(\tilde{u}\left(t\right)\tilde{H}|\psi \left({\tau }_k^{-}\right)\rangle \right),P\phi \left(\tilde{u}\left(t\right)\tilde{H}|\psi \left({\tau }_k^{-}\right)\rangle \right)\rangle \right)}^2\\ \le V\left({\tau }_k^{-},e\left({\tau }_k^{-}\right)\right)+e\left({\tau }_k^{-}\right)l^2\tilde{u}\left(t\right)\langle \psi \left({\tau }_k^{-}\right)|{\tilde{H}}^{\text{T}}P\tilde{H}|\psi \left({\tau }_k^{-}\right)\rangle \\ +\frac{1}{2}{l}^4{\tilde{u}}^2\left(t\right){\left(\langle \psi \left({\tau }_k^{-}\right)|{\tilde{H}}^{T}P\tilde{H}|\psi \left({\tau }_k^{-}\right)\rangle \right)}^2\end{array}$ (17)

其中

$\langle \psi \left({\tau }_k^{-}\right)|{\tilde{H}}^{\text{T}}P\tilde{H}|\psi \left({\tau }_k^{-}\right)\rangle \le {\Vert |\psi \left({\tau }_k^{-}\right)\rangle \Vert }^2\Vert {\tilde{H}}^{\text{T}}P\tilde{H}\Vert \le \sqrt{\text{Tr}\left(P{\tilde{H}}^{2}P{\tilde{H}}^2\right)}$ (18)

将(18)代入(17)，整理后可得

$V\left({\tau }_k,e\left({\tau }_k\right)\right)-V\left({\tau }_k^{-},e\left({\tau }_k^{-}\right)\right)\le e\left({\tau }_k^{-}\right)l^2\tilde{u}\left(t\right)\sqrt{\mathrm{Tr}\left(P{\tilde{H}}^{2}P{\tilde{H}}^2\right)}+\frac{1}{2}{l}^4{\tilde{u}}^2\left(t\right)\mathrm{Tr}\left(P{\tilde{H}}^{2}P{\tilde{H}}^2\right)$ (19)

令 $\kappa =l^2\sqrt{\mathrm{Tr}\left(P{\tilde{H}}^{2}P{\tilde{H}}^2\right)}$，且取

$\tilde{u}\left(t\right)=\frac{-e\left({\tau }_k^{-}\right)-\sqrt{e^2\left({\tau }_k^{-}\right)-\tilde{\gamma }{\left|e\left({\tau }_k^{-}\right)\right|}^{\beta +1}}}{\kappa }$， (20)

其中满足条件 ${\left|e\left({\tau }_k^{-}\right)\right|}^{\beta -1}\le \frac{1}{\tilde{\gamma }}$，则

$V\left({\tau }_k,e\left({\tau }_k\right)\right)-V\left({\tau }_k^{-},e\left({\tau }_k^{-}\right)\right)\le -\frac{1}{2}\tilde{\gamma }{\left|e\left({\tau }_k^{-}\right)\right|}^{\beta +1}\le -\frac{1}{2}\tilde{\gamma }{\left(e^2\left({\tau }_k^{-}\right)\right)}^{\frac{\beta +1}{2}}=-{\gamma }_{2}V{\left({\tau }_k^{-},e\left({\tau }_k^{-}\right)\right)}^{\frac{\beta +1}{2}}$

其中 ${\gamma }_2=2^{\frac{\beta -1}{2}}\tilde{\gamma }$。

根据引理1，上述结果表明在跟踪控制律(12)和(14)的作用下，误差动态系统在有限时间内收敛到0，

而该有限时间可由 $t_0=\frac{V^{1-0.5\left(1+\beta \right)}\left(0\right)}{2{\gamma }_0\left(1-0.5\left(1+\beta \right)\right)}$ 来估计，其中 ${\gamma }_0=\max \left\{{\gamma }_1,{\gamma }_2\right\}$。

换言之，在非线性脉冲控制场作用下，封闭量子系统在有限时间 $t_0$ 跟踪并到达目标函数 $s\left(t\right)$。

若仅考虑线性脉冲控制场，则封闭量子系统(2)可简化为如下形式：

$\{\begin{array}{l}i|\stackrel{\dot{}}{\psi }\left(t\right)\rangle =H|\psi \left(t\right)\rangle ,t\ne {\tau }_k\\ \Delta |\psi \left(t\right)\rangle =\tilde{u}\left(t\right)\tilde{H}|\psi \left({\tau }_k^{-}\right)\rangle ,t={\tau }_k\end{array}$

不难由定理1导出以下结论。

推论1考虑跟踪控制律 $u_1\left(t\right)=\frac{I_0}{2I_1+{\epsilon }_1}$ 、 $u_2\left(t\right)=\gamma e\left(t\right)\left(I_2+{\epsilon }_2\right)$ 以及 $\tilde{u}\left(t\right)=-\frac{2e\left({\tau }_k^{-}\right)}{\kappa }$，则跟踪误差系统 (7)指数稳定，并快速收敛到0，其中 $V\left(0\right)=\frac{1}{2}{e}^2\left(0\right)$。

证明过程与定理1类似，故省略。

4. 数值例子

下面，通过一个数值例子及其仿真来说明所得结论的有效性。

考虑一个四能级的量子系统，控制系统的自由Hamiltonian量为：

$H_0=\mathrm{diag}\left(0.3174,1.6253,2.4136,3.8361\right)$。

对于此四阶系统，我们假设任意两个能级之间都有相互作用。考虑到上述设计的控制律，假设三个外部控制Hamiltonian量为以下形式：

$H_1=\left[\begin{array}{cccc}0& 1& 0& 1\\ 1& 0& 1& 0\\ 0& 1& 0& 1\\ 1& 0& 1& 0\end{array}\right]$， $H_2=\left[\begin{array}{cccc}0& 1& 1& 0\\ 1& 0& 0& 1\\ 1& 0& 0& 1\\ 0& 1& 1& 0\end{array}\right]$， $\tilde{H}=\left[\begin{array}{cccc}0& 0& 1& 1\\ 0& 0& 1& 1\\ 1& 1& 0& 0\\ 1& 1& 0& 0\end{array}\right]$

于是，系统的Hamiltonian量为：

$H=H_0+u_1\left(t\right)H_1+u_2\left(t\right)H_2$。

自由Hamiltonian量 $H_0$ 的本征值分别为 ${\lambda }_1=0.3174$， ${\lambda }_2=1.6253$， ${\lambda }_3=2.4136$， ${\lambda }_4=3.8361$，相应的本征态分别为： $|{\lambda }_1\rangle ={\left[1,0,0,0\right]}^{\text{T}}$， $|{\lambda }_2\rangle ={\left[0,1,0,0\right]}^{\text{T}}$， $|{\lambda }_3\rangle ={\left[0,0,1,0\right]}^{\text{T}}$， $|{\lambda }_4\rangle ={\left[0,0,0,1\right]}^{\text{T}}$。

仿真实验中，观测算符取为 $P=|{\lambda }_1\rangle \langle {\lambda }_1|=\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\end{array}\right]$，选取被控系统的初态为 $|{\lambda }_1\rangle$, $|{\lambda }_2\rangle$, $|{\lambda }_3\rangle$ 和 $|{\lambda }_4\rangle$ 的叠加态，可以表示为：

$|{\psi }_0\rangle =\frac{1}{2}|{\lambda }_1\rangle +\frac{1}{2}|{\lambda }_2\rangle +\frac{1}{2}|{\lambda }_3\rangle +\frac{1}{2}|{\lambda }_4\rangle$。

初始输出为 $y\left(0\right)=\langle {\psi }_0|P|{\psi }_0\rangle =0.35$。对于目标函数 $s\left(t\right)=\arctan \left(2\pi t+0.5\right)$，其初值为 $s\left(0\right)=0.4636$。于是，误差的初始值为 $e\left(0\right)=s\left(0\right)-y\left(0\right)=0.1136$。取控制增益为 $\gamma =2$ 及 $\tilde{\gamma }=0.4$。选取 $\beta$ 为0.6。于是， ${\gamma }_1=6.9644$， ${\gamma }_2=0.3482$。 $l=2.5$。控制律的初始值为 $u_1\left(0\right)=u_2\left(0\right)=0.005$， $u_3\left(0\right)=0.5$。

图1刻画了跟踪误差系统的演化规律。不难看出，在控制律作用下，该动态误差系统能够在有限时间内快速收敛到0。图2和图3分别表示外部控制律 $u_1\left(t\right)$ 和 $u_2\left(t\right)$。其中图2中的控制律用于抵消误差系统中的漂移项，而图3中展示的是改进的有限时间控制律。图4则表示脉冲控制场中的外部控制律 $\tilde{u}\left(t\right)$。

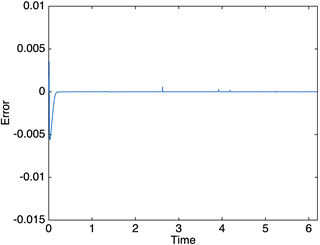
Figure 1. Evolution of the error $e(\; t\; )$

图1. 误差 $e\left(t\right)$ 的演化

Figure 2. Control law $u_1(\; t\; )$

图2. 控制律 $u_1(\; t\; )$

Figure 3. Control law $u_2(\; t\; )$

图3. 控制律 $u_2(\; t\; )$

Figure 4. Control law $\tilde{u}(\; t\; )$

图4. 控制律 $\tilde{u}(\; t\; )$

图5展示了控制系统的误差与控制增益、控制边界之间的关系。从图5上可以看出，这种关系很复杂，没有简单的规律可循。不过，图5仍然可以在直观上反映控制参数对控制系统误差的影响。

Figure 5. The relations between the error of the control system and the control gain and control boundary

图5. 控制系统的误差与控制增益、控制边界之间的关系

5. 结论

本文研究了一类在脉冲控制场作用下封闭量子系统的轨迹跟踪问题。利用Lyapnov直接法，通过设计改进的消除漂移控制律、有限时间跟踪控制律以及非线性脉冲控制律，使得封闭量子系统的状态能够在外部控制律的作用下快速进入有界时变目标系统的轨迹。数值仿真以四阶量子系统为例，通过引入外部跟踪控制策略，进行仿真实验。实验结果表明，误差动态系统在任意初始状态下能够在有限时间内收敛到0，从而达到预期的跟踪精度，且具有更好的抗干扰能力。

基金项目

本研究得到了江苏省高等学校自然科学研究面上项目(编号：17KJB510051)、江苏高校“青蓝工程”(中青年学术带头人(2022)、优秀教学团队(2020))、无锡市科协软科学研究课题(编号：KX-22-B60)、江苏省高职院校教师专业带头人高端研修(个人访学研修) (编号：2021GRFX068)资助支持。