1. 引言
初等数学中许多问题提出的本意是为了使学生进一步获得未来发展所必须的数学基础知识、基本技能及基本思想,提高学生从数学的角度去思考和解决问题的能力,目的在于发展学生数学抽象、逻辑推理、数学运算、数据分析等核心素养,最终让学生有自主学习、善于思考的意识 [1]。由于不同的人对数学上有不同的思考方式,学生对数学问题的分析也会不尽相同,因而不同的知识储备和分析问题的能力让学生面对同一题目会产生“一题多解”的情况。
“一题多解”是从不同角度分析问题,根据所给信息,运用已有的数学知识、经验,通过观察、推测和想象,沿着不同方向思考、重组已有信息,获得多种解法的过程 [2]。
在本科生“数学解题研究与实践”课程的教学实践中发现不同学生对同一道数学问题有不同的理解能力与解题方法,学生们会产生两种解题状况,一种是对问题毫无思绪,另一种是通过深入分析,联想到许多解题方法。大部分学生能利用一种或两种初等数学方法解决问题,但极少数学生能利用高等数学知识更简洁化解决初等数学问题。通过观察和调查可知,这种差异产生的主要原因是学生不同的知识水平。在中学时期所学知识水平有限,很少有学生会思考用多种方法解决同一问题,这就使得学生的思维存在非常大的局限性,这种惯性思维使得很少有本科学生联想利用高等数学知识来解决初等数学问题。因此如何提高学生自主思考、提高解决问题的能力,培养学生“一题多解”的意识是教师急需解决的问题。
在以往的初等数学解题教学实践中,教师只要学生解答问题,并不注重学生思维方式的培养。自基础教育课程改革实施以来,一线教师已逐步意识到素质教育的重要性,最大限度地提高了教学效率和教育质量,尤其更加注重学生数学思维方式培养。近年来,以“高观点”为背景的数学试题已经出现在高中生的视野之中,“高观点”是19世纪末20世纪初数学家菲力克斯·克莱因在《高观点下的初等数学》中提出的,指运用高等数学的知识、方法、思想等去分析和解决初等数学问题的思想 [3]。本文从“高观点”的角度去刨析一道初等数学问题,分析初等数学问题高等化的必要性。
2. 试题呈现
已知
均为正实数,且
,求证:
3. 解法分析
接下来我们就以上面的试题为例,从不同角度分析问题,根据所给信息,运用已有的数学知识、经验,通过观察、推测和想象,沿着不同方向思考、重组已有信息。
从结构上看,学生根据已有的知识经验看到
会联想到勾股定理和圆的方程,进而从几何
的角度寻找解题方法,基础好一些的同学会联想到极坐标;当观察结论
时,又联想到均值
不等式,极少数学生会想到柯西不等式和拉格朗日乘数的方法,柯西不等式和拉格朗日乘数属于高等数学范畴,这也说明大部分学生遇到初等数学问题时仍会选择初等数学知识解决问题,缺少“一题多解”和利用高等数学知识去解决问题的意识,根据思考的维度不同,解题方法呈现如下:
解法1:从代数的角度联想到均值不等式。
分析
可以得到,
,
显然成立,即
成立。
解法2:从几何角度联想到点到直线的距离公式。
将
看成以
为圆心,z为半径的圆弧,由于题干中给出
,
,
,观察
可联想其可以表示从圆弧上任取一点
到直线
的距离l (如图1),显然
,因此
成立。
解法3:从极坐标变换的角度
设
,
为参数,
,代入
得:
,
其中
。当
时,
取得最大值1,因此可得
,故
成立。
解法4:从解三角形的角度
令
,
,
,
,代入得:
,
即
成立。
解法5:从平面几何的角度
待求证式子可以看成
,
于是联想到关于圆内接四边形的托勒密(Ptolemy)定理,
只要令
,
,
(AC为圆的直径,如图2),
,
,就可以用托勒密定理加以证明。
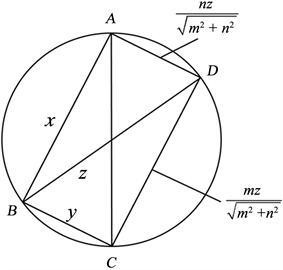
Figure 2. Schematic diagram of a quadrilateral in a circle
图2. 圆内接四边形示意图
解法6:从不等式求解的角度联想到Cauchy不等式
要证
,只需证
,即
,
根据Cauchy不等式显然成立。
解法7:联想到Larange乘数
设算子
,对L分别求关于变量
的偏导数,再令
求极值点,证明
即可。
4. 解后反思
以上7种解法可以看出此题用初等数学知识是非常容易得证的,但是由于学生的思维比较局限,想不到高等数学知识对此题的帮助,得不到更多的解法思路。一道题可以从多角度观察分析得出多种解题方法,观点越高,解题方法也就越多,因此如何提高学生的解题能力、培养学生“一题多解”的意识以及用更高的观点去审视问题是值得教师去思考的。
鉴于以上分析,对中学教师的解题教学提出以下两点建议:
第一,解题教学中要引导学生参与思考,从多方面分析问题,让学生熟练掌握和使用基础知识解决问题,同时培养学生面对问题联想所学知识的意识,引发学生对同一问题的多角度思考,从而引发学生“一题多解”的行为。
第二,不同层次的学生可相应增设不同的课外知识点,即高等数学知识,丰富学生的知识模块,培养学生从更高的观点看待问题的意识。这些知识不需要学生完全掌握,只需学生知道和了解,并能简单应用即可。比如在本题中,可以给学生介绍Cauchy不等式
的形式,再者可以将Cauchy不等式简化到二维形式:
设
均为实数,则
,
二维形式更有助于学生理解,最后可以让学生简记为“平方的和的积大于等于积的和的平方”。学生通过对Cauchy不等式的了解,达到可以利用Cauchy不等式解决问题水平。这种教学方式不仅能让学生感受到解决问题的方法之多,彰显出高等数学知识的“高级”之处,还能够激发出学生对数学知识的渴望,培养学生从不同角度分析问题的意识,丰富了学生已有的数学知识、经验,利于培养学生获得多种解法意识。
由此可见学生多了解或者掌握一些高等数学知识是十分必要的。中学数学教师或是师范院校的师范生,如果能够在不增加学生负担的情况下,让学生多了解和掌握一些“更高级”的定理,便能居高临下的看待数学问题,触发出更多的解题“火花”。
基金项目
伊犁师范大学资助项目:“初等数学研究”教学中创新意识与应用能力培养的研究与实践(项目编号:YSYB2022109)。