1. 引言
“圆周角定理”的内容具有一定的抽象性,对逻辑思维能力有一定的要求,在整个教材中具有承上启下的重要作用,在学习过程中可以有助于提高学生的几何思维水平。而几何思维水平的提高并非一蹴而就的,需要教师意识到“数学教学不仅要使学生掌握知识,而且要使学生掌握思想方法,发展思维品质”“教学要关注过程”等等 [1]。本文将通过范希尔理论的五个水平依次展开说明,将“圆周角定理”中的几个教学片段与范希尔理论的五个水平相对应,循序渐进地设计“圆周角定理”的教学过程,激发学生的逻辑思维,并最终实现学生几何思维水平的提升以及促进学生的全面优质发展。
2. 范希尔理论概述
范希尔理论是范希尔夫妇在皮亚杰认知理论的基础上,结合自身长期教学实践总结出来用来刻画学生几何思维水平的理论,它在几何教学领域有着广泛的影响。
范希尔理论的核心内容有两个,一是几何思维的五个水平,二是与之对应的五个教学阶段。其中的五个水平由低到高依次是:视觉水平、分析水平、非形式化的演绎水平、形式化的演绎水平、严密性水平 [2]。而与之相对应的五个教学阶段是:学前咨询阶段、引导定向阶段、阐明阶段、活动阶段以及整合阶段 [3]。范希尔认为几何思维水平的发展是具有顺序性的,五个水平是既不能被跳跃,也不能被调整次序,学生必须达到前一水平才能通过教育进入后一水平 [4]。
因此,教师在培养与训练学生几何思维的过程中,可以按照范希尔理论的五个水平之间的层次来设计教案并展开教学活动,使得学生对几何的学习拥有更多的好奇心与信心,并提升学生的几何思维水平。
3. 范希尔理论的具体运用
本文选取的是浙教版九年级数学上册第三章“圆的基本性质”第五节内容——“圆周角定理”,这节内容是提升几何思维水平的重要环节。从圆中抽象出圆心角与圆周角之间的数学关系,将两者紧密联系起来,便于学生加强对圆的基础的学习,同时也为圆内接四边形的学习打下基础。
3.1. 在分类中激活视觉水平,在描述中过渡到分析水平
范希尔理论认为处于视觉水平的学生能够通过图形的整体轮廓进行辨认,能够通过画图进行模仿,使用标准或者不标准的名称描述几何图形。而处于分析水平的学生能够分析图形的基本特征,了解图形的定义 [5]。学生在学习“圆周角定理”这节课之前,已经学习过了圆的基本内容以及圆心角部分内容,对圆的认识已经达到了一定的视觉水平,能够通过细节进行比较分类,以激活学生的原有视觉水平。而在学生直观分类后,教师可以引导学生认识新的知识——圆周角,并根据图形的基本特征描述图形的概念,从而使得学生的几何思维水平由视觉水平过渡到分析水平。
【片段1】观察图形,直观分类,探究特征,构建概念
课件出示:(图1)
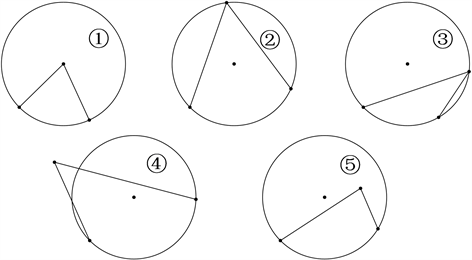
Figure 1. Comparative classification chart of circumferential angles
图1. 圆周角的比较分析图
师:老师在黑板上画了5个图形,请同学们观察一下,它们有什么异同点?
生1:它们都是一个圆和两条直线。
生2:它们的交点位置不同。
师:那能将这5个图形进行分类吗?
生:将图①分一类,它的交点在圆心,出现了圆心角;图②、图③分为一类,它的交点在圆上;图④、图⑤分为一类,它的交点既不在圆心也不在圆上。
师:今天这节课我们就来认识图②、图③,它们所形成的角叫圆周角。那什么是圆周角呢?
生:圆周角是圆上有一点,过这个点有两条直线与圆相交所形成的角。
师:我们用研究数学语言可以这么定义:圆周角是指顶点在圆上,且两边和圆相交的角。
【思考】教师让学生观察比较上述5个图形,由于学生在这之前已经学习了圆心角,对图形有一定的概念,能够区分出图①和图④、图⑤。教师需要引导学生发现新的内容,对圆周角组成的基本要素有一定的认识,能够模仿画出图形。学生在找到图形的不同点后,尝试给出圆周角的定理,教师在过程中帮助学生构建圆周角的概念,为进一步学习圆周角部分的内容提供学习素材。
上述过程中,学生对圆周角有了一定的直观感知,通过之前所学的圆心角,激发了对原有图形的几何思维水平——视觉水平,在观察比较中能够模糊地感知圆心角与圆周角之间的区别。区分出上述图形的异同点,归纳出圆周角的基本要素与特征,根据特征构建圆周角的概念,是学生能够达到分析水平。
3.2. 关联中提升到非形式化的演绎水平
范希尔理论认为,处于非形式化的演绎水平的学生能够理解图形性质之间的关联,有能力进一步探究图形之间的内在属性与关联关系。在学生了解圆周角的定义之后,教师可以通过将圆心角与圆周角放在同圆等弧之中,让学生对两者之间的内在属性进行关联,从而使得学生的几何思维水平由视觉水平、分析水平提升至非形式化的演绎水平。
【片段2】操作感知,相互关联(图2)
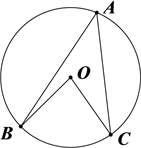
Figure 2. Plot of the relationship between the central angle and the circumferential angle
图2. 圆心角与圆周角之间的关系图
师:我们将圆心角与圆周角放在同一个圆上,并且它们所对的弧相同。那么同学们你们觉得圆心角与圆周角之间有什么关系呢?(引导学生可以通过量角器测量圆心角与圆周角的度数)
生:圆周角的度数等于圆心角度数的一半。
师:那如果角的位置与度数都发生变化,那么上述结果还存在吗?(引导学生自主多次画图并测量不同情况下角的度数)
生:仍然成立!
师:经过大家的测量,我们可以猜想得到:圆周角的度数等于它所对弧上的圆心角度数的一半。我们将这个定理称作“圆周角定理”。
【思考】教师引导学生发现圆心角与圆周角之间存在的数量关系,让学生自己画图、动手测量圆心角与圆周角的度数,在学生自己操作感知的过程中,将看似无关的两个数学元素相互关联起来。教师再进一步引导学生猜想得到圆周角定理,提升学生在几何方面的演绎水平。
上述过程中,学生多次画图、测量度数、合理猜想,理解同圆等弧所对的圆心角与圆周角之间的关联,最终得到圆周角定理。在这一教学片段过程中,能够促使学生对圆周角的认知水平由视觉水平、分析水平提升至非形式化的演绎水平。
3.3. 严谨证明下达到形式化的演绎水平
范希尔理论认为,处于形式化的演绎水平的学生能够用演绎推理的形式证明几何问题,有能力根据已有知识对陌生或多种情况的几何问题进行证明。在这之前,学生已经初步猜想得到了圆周角定理,那么接下来就需要对定理进行严谨地证明。在教师的教学辅助下,使学生的几何思维水平由非形式化的演绎水平提升至形式化的演绎水平。
【片段3】演绎推理,证明定理
师:我们已经猜想得到了圆周角定理,那么我们如何对此进行严谨地证明呢?
生:圆心角与圆周角之间有多种情况,要分类证明?
师:那么究竟有几种不同的情况呢?大家先自己画图进行分类吧。(学生自主进行分类)
生1:2种。
生2:3种。
师:究竟有多少种呢?让我们通过软件进行动态的演示,看看到底是2种还是3种。(教师展示几何画板中的动态过程)我们发现一共有3种情况,分别是圆心O圆周角
的一边
上,在圆周角
的内部以及在圆周角
的外部。那么我们需要对每一种情况都进行证明。首先是第一种情况,它相对来说比较简单,大家尝试用已有的知识进行证明吧。
教师在黑板上画出第一种情况的图形,见图3:
(学生进行自主证明)
师:很好,大多数同学已经证明出来了,那么老师在黑板上将第一种证明的过程完整讲述,大家看看是否和老师的想法一致。(教师进行板演)那么同学们再尝试一下对第二种情况的证明。
(学生进行自主证明)
师:好,那么我们来看看如何进行证明,我看同学们很多都是通过遮挡法来进行证明的,那么我们请一位同学来讲解一下。
教师根据学生的表达操作演示,见图4:
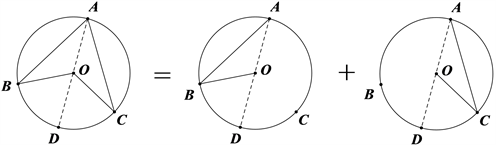
Figure 4. The blocking method of the second case
图4. 第二种情况的遮挡方式
师:我们是不是发现第二种情况就是和第一种情况类似,分两部分进行证明。那么同学们再看看第三种情况,是不是也是同样的道理。请同学们自主进行证明。
……
【思考】学生探索分多少“类”进行讨论,教师鼓励学生通过已有的知识对圆周角定理的三种情况进行证明,从而巩固加深对圆周角定理的理解,使得学生通过演绎推理的方式提高自身的几何思维水平。
上述过程中,学生自主证明圆周角定理,教师在此过程中起到辅助作用,帮助学生进行完整地分类讨论、通过添加辅助线完成证明。在这样的学习过程中,学生对知识的认识与理解由非形式化的演绎水平提升至形式化的演绎水平。
3.4. 在试题中冲刺严密性水平
范希尔理论认为,处于严密性水平的学生能够在新定义的几何试题背景下,严谨地证明或解决数学问题。在这一阶段之前,学生已经熟练掌握圆周角定理的内容与证明,达到了几何思维水平中的形式化的演绎水平。在此之后,教师需要通过给学生一定的试题,让学生在新的几何试题背景下,尝试灵活运用与结合圆周角定理的相关内容来证明或解决相关的数学问题,继而使得学生的几何思维水平由形式化的演绎水平提升至严密性水平。
4. 结语
教师要秉承“学生为主体”的教育理念,合理设计教学方案,保证课堂教学质量,提升学生的几何思维水平。而如何提升学生的几何思维水平、如何通过教学锻炼学生几何思维的敏锐性、严谨性与逻辑性,这些都是众多教师应当思考的重要问题。本文对范希尔理论以及其几何思维的五个水平:视觉水平、分析水平、非形式化的演绎水平、形式化的演绎水平和严密性水平,进行了简要的介绍。而后基于范希尔理论中的几何思维的五个水平依次讲解,通过一些教学片段的展示来阐述如何依次提升学生的几何思维水平,帮助学生实现不同思维水平之间的过渡,在教学实践中使得学生一步步接触到严密性水平,激发学生对几何学习的兴趣与信心。
致谢
最后,感谢学校教师提供的悉心指导和积极帮助,同时也对参考文献中的思想和方法的所有者表示最真挚的谢意。