基于贝叶斯推断的缓冲自回归模型参数估计

Parameter Estimation of Buffered Autoregressive Model Based on Bayesian Inference

摘要: 本文基于马尔科夫链蒙特卡罗(MCMC)算法的贝叶斯推断下，研究缓冲自回归模型的参数估计问题。通过缓冲自回归模型参数的联合后验分布得到各参数的条件后验分布，再利用Gibbs抽样、随机游走Metropolis-Hastings算法抽取样本，并以正态分布为建议分布，对缓冲自回归模型进行参数估计。随机模拟结果显示用该方法估计各参数的效果较好。

Abstract: Based on Bayesian inference of Markov chain Monte Carlo (MCMC) algorithm, this paper studies the parameter estimation of buffered autoregressive models. The conditional posterior distribution of each parameter is obtained through the joint posterior distribution of the parameters of the buffered autoregressive model. Then, the Gibbs sampling and random walk Metropolis Hastings algorithm are used to extract samples, and the normal distribution is used as the suggested distribution to estimate the parameters of the buffered autoregressive model. The results of stochastic simulation show that the method is effective in estimating the parameters.

1. 引言

时间序列分析作为一个非常有效的研究实际问题的方法，在过去的20多年间，前人对时间序列模型进行了大量的理论与实证研究。但随着经济社会的快速发展，Clements和Hansen等人发现，经典的线性自回归时间序列模型不再适用于经济和金融时间序列的研究 [1] [2] ，难以解释金融时间序列中的非线性结构变化，非线性的时间序列模型也因此应运而生。门限自回归(TAR)模型作为非线性时间序列模型中成熟的代表，自Tong开创性的引入TAR模型以来 [3] ，门限型时间序列模型在经济、环境等领域的研究发挥了重要作用。传统的门限自回归模型根据门限变量的状态变化将时间序列划分为两个甚至更多的不同区域，并在每个区域建立不同的线性自回归模型。当门限变量超过或低于某个值时，时间序列的概率结构突然发生变化。但是在一些领域中，例如经济学、地理学等，我们经常观察到状态转变的缓冲现象，即当门限变量超出或低于限制区域时，我们感兴趣的变量仍停留在前一状态保持不变。Li等人将这种缓冲现象引入到门限自回归模型当中 [4] 。同时，考虑到在金融时间序列模型中，条件异方差是一个极其重要的部分，Lo等人在汇率研究中提出了缓冲GARCH模型 [5] 。Zhu等人随后也介绍了具有广义自回归条件异方差的缓冲自回归模型 [6] ，并通过汇率分析，将其与AR-GARCH和T-GARCH模型进行了对比，进一步说明了缓冲自回归GARCH模型在刻画时间序列模型中的条件均值与方差的优越性。

Markov链Monte Carlo (MCMC)算法作为现代统计计算中重要的一种方法，主要利用马尔科夫链的细致平衡条件进行采样，再通过所采样的样本进行数值计算的一种方法。过去的许多研究员，为了简化TAR、TARMA等模型统计推断中的分析工作和数值多重积分问题，均使用MCMC方法来估计模型的未知参数，不仅相对快速地的估计出模型参数，同时对比其他方法，提高了估计的精度。早在Chen和Lee中，马尔科夫链蒙特卡罗(MCMC)算法就被用于门限自回归模型的贝叶斯推断 [7] 。So则利用可逆跳MCMC算法检验GARCH和TGARCH模型 [8] 。不管是对门限参数估计还是对其他参数估计，MCMC算法都显示出了较好的效果。

过去的研究主要集中在缓冲自回归模型的应用方面，而对该模型的参数估计及检验研究较少，特别是结合MCMC算法与贝叶斯推断的方法寥寥无几。而基于过往研究的基础，我们对模型进行贝叶斯推断后，我们主要利用Gibbs抽样和随机游走的Metropolis-Hastings (M-H)算法的MCMC方法对缓冲自回归模型做参数估计，得到参数估计结果落在95%置信区间内，证明结果是可靠和有效的。

2. 模型描述

我们定义如下的缓冲自回归模型：对于序列 $\left\{y_t,t=1,2,\cdots ,n\right\}$ ，

$y_t=\{\begin{array}{cc}{\psi }_0+{\displaystyle \underset{i=1}{\overset{p}{\sum }}{\psi }_i{y}_{t-i}+a_t,}& R_t=1,\\ {\phi }_0+{\displaystyle \underset{i=1}{\overset{p}{\sum }}{\phi }_i{y}_{t-i}+a_t,}& R_t=0,\end{array}$

其中，状态参数 $R_t$ 定义如下：

$R_t=\{\begin{array}{ll}1\hfill & \text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}{y}_{t-d}\le r_L\hfill \\ 0\hfill & y_{t-d}\ge r_U\hfill \\ R_{t-1}\hfill & 其他\hfill \end{array}$

其中， $a_t,t=1,2,\cdots ,n$ 相互独立，其均值为0，方差为 ${\sigma }^2$ ； $y_{t-d}$ 为门限变量；d是延迟参数； $r_L$ 和 $r_U$ 是缓冲区 $\left(r_L,r_U\right]$ 的门限参数。对于现实中的时间序列 $\left\{y_t\right\}$ ，考虑到前几个观测值的状态可能无法很好地识别，我们很自然地假设， $\left(r_L,r_U\right]$ 为 $\left[a,b\right]$ 的子集， $a,b$ 为门限变量 $y_{t-d}$ 数据样本的上下 $\alpha$ 经验分位数 [9] [10] 。

3. 贝叶斯推断

为了对参数进行抽样，我们需要求得各个参数的条件后验分布结果，同时，各参数条件后验分布形式决定了参数所使用的抽样方式。根据共轭先验分布的特点，我们进行如下设定：

设 $y_t$ 由 $t=1$ 时刻开始观察，记：

$\begin{array}{l}{\psi }_1={\left({\psi }_0,{\psi }_1,\cdots ,{\psi }_p\right)}^{\text{T}},{\psi }_2={\left({\phi }_0,{\phi }_1,\cdots ,{\phi }_p\right)}^{\text{T}},\\ \gamma ={\left(r_L,r_U\right)}^{\text{T}},Y=\left\{y_1,y_2,\cdots ,y_n\right\}\end{array}$

则 $y_t$ 的条件均值可得：

${\mu }_t=E\left[y_t|Y_{\left(t-1\right)}\right]=\left[{\psi }_0+{\displaystyle \underset{i=1}{\overset{p}{\sum }}{\psi }_i{y}_{t-i}}\right]R_t+\left[{\phi }_0+{\displaystyle \underset{i=1}{\overset{p}{\sum }}{\phi }_i{y}_{t-i}}\right]\left(1-R_t\right)$

其中， $Y_{\left(t-1\right)}={\left(y_{t-1},\cdots ,y_{t-p}\right)}^{\text{T}}$ 。

记 $\Psi ={\left({\psi }_1,{\psi }_2,\gamma ,\sigma ,d\right)}^{\text{T}}$ 为待估的参数向量。我们利用贝叶斯推断得到各参数的条件后验分布，再根据条件后验分布的情况，选择合适的MCMC方法进行参数估计。

对于未知参数，我们选择的先验分布如下：

1) ${\psi }_1,{\psi }_2$ 相互独立， ${\psi }_j~N\left({\psi }_{j0},V_j^{-1}\right),j=\text{1,2}$ ，其中 ${\psi }_{j0},V_j^{-1}$ 为正态分布的均值向量和协方差矩阵；

2) ${\sigma }^2$ 服从逆伽马分布 $IG\left(\alpha ,\beta \right)$ ；

3) 门限参数 $r_L,r_U$ 服从 $\left[a,b\right]$ 上的均匀分布，且 $a\le r_L<r_U\le b$ ；

4) 延迟参数d服从 $1,2,\cdots ,d_0$ 上离散的均匀分布，且 $d_0$ 数值较大。

以上各先验分布得超参数已知，根据贝叶斯公式，可推出 $\Psi$ 的先验分布满足：

$p\left(\Psi \right)\propto {\displaystyle \underset{j=1}{\overset{2}{\prod }}p\left({\psi }_j\right)p\left({\sigma }^2\right)I\left(a<r_L\le r_U\le b\right)}$

可得 $\Psi$ 的联合后验分布为：

$p\left(\Psi |y\right)\propto p\left(y|\Psi \right)p(\; \Psi \; )$

模型的似然函数为：

$p\left(\Psi |y\right)\propto {\displaystyle \underset{t=d_0+1}{\overset{n}{\prod }}\frac{1}{\sqrt{2\pi }}\frac{1}{a_t}\left\{\left[\frac{{\left(y_t-u_{t1}\right)}^2}{2a_t^2}\right]\cdot R_t+\left[\frac{{\left(y_t-u_{t2}\right)}^2}{2a_t^2}\right]\cdot \left(1-R_t\right)\right\}}$

其中，

$u_{ti}=E\left(y_{ti}|y_{ti-1}\right)=\{\begin{array}{cc}{\psi }_0+{\displaystyle \underset{i=1}{\overset{p}{\sum }}{\psi }_i{y}_{t-i}+a_t,}& i=1\\ {\phi }_0+{\displaystyle \underset{i=1}{\overset{p}{\sum }}{\phi }_i{y}_{t-i}+a_t,}& i=2\end{array}$

根据贝叶斯定理，计算各参数后验分布如下：

1) ${\psi }_j,j=1,2$ 条件后验分布相互独立且服从正态分布：

$p\left({\psi }_j|y,\Psi -{\psi }_j\right)~N\left({\psi }_{{}_{j0}}^{*},V_j^{*-1}\right),j=\text{1,2}$

其中

${\psi }_{j0}^{*}={\left(\frac{A_i}{{\sigma }^2}+V_j\right)}^{-1}\left(\frac{A{}_i}{{\sigma }^2}{\hat{\psi }}_j+V{\psi }_{j0}\right),V_j^{*}=\left(\frac{A_i}{{\sigma }^2}+V_j\right)$

$\begin{array}{l}{x}_{j,t}={\left(1,y_{t-1},\cdots ,y_{t-h}\right)}^{\text{T}},X_1^{*}={\left(x_{1,h+1},x_{1,h+2},\cdots x_{1,\tau }\right)}^{\text{T}},\\ X_2^{*}={\left(x_{2,\tau +1},x_{2,\tau +2},\cdots ,x_2,n\right)}^{\text{T}},Y_1^{*}={\left(y_{h+1},y_{h+2},\cdots ,y_{\tau }\right)}^{\text{T}},\\ Y_2^{*}={\left(y_{\tau +1},y_{y+2},\cdots ,y_n\right)}^{\text{T}},A_i=X_i^{*\text{T}}{X}_i^{*},\\ {\hat{\psi }}_j=A_i^{-1}{X}_i^{*\text{T}}{Y}_i^{*}.\end{array}$

2) ${\sigma }^2$ 条件后验分布为逆伽马分布：

$p\left({\sigma }^2|y,\Psi -{\sigma }^2\right)~IG\left(\alpha +\frac{n-p}{2},\beta \text{+}\frac{s^2}{2}\right),$

其中，

$s^2={\displaystyle \underset{i=1}{\overset{2}{\sum }}{\left(Y_i^{*}-X_i^{*\text{T}}{\psi }_i\right)}^{\text{T}}\left(Y_i^{*}-X_i^{*\text{T}}{\psi }_i\right)}.$

3) $\gamma$ 的条件后验密度函数为：

$p\left(\gamma |y,\Psi -\gamma \right)\propto \exp \left(-\frac{1}{2{\sigma }^2}\cdot s^2\right)\cdot I\left(a<r_L<r_U<b\right),$

其中 $s^2$ 是关于r的函数。

4) d条件后验分布为多项分布，密度函数为：

$p\left(d|y,\Psi -d\right)=\frac{L\left({\psi }_1,{\psi }_2,{\sigma }^2,\gamma ,d|y\right)}{{\displaystyle \underset{d=1}{\overset{d_0}{\sum }}L\left({\psi }_1,{\psi }_2,{\sigma }^2,\gamma ,d|y\right)}},$

其中， $L\left({\psi }_1,{\psi }_2,{\sigma }^2,\gamma ,d|y\right)={\sigma }^{n-p}\exp \left(-\frac{s^2}{2{\sigma }^2}\right)$ 。

综上，我们可看出，除了门限参数向量 $\gamma$ 的条件后验分布不是标准分布，其余参数的条件后验分布均是常见的分布，因此可以利用Gibbs抽样。而对门限参数向量采用随机游走的Metropolis-Hasting抽样的MCMC方法 [11] 。

我们以 $\gamma$ 为例，记 $f(·)$ 为其条件后验密度函数。M-H算法的基本思想是通过在参数空间随机取值作为起始点，通过建议函数与转移概率构建一个细致平稳的马尔科夫链，使得 $f(·)$ 成为稳定分布，并通过获得的随机点与起始点概率密度的比值大小决定是否保留随机点。则利用随机游走的M-H抽样步骤如下 [12] ：

1) 在第l步迭代时，通过建议分布产生一个 $\gamma$ 候选值 ${\gamma }^{*}$ ，使其满足：

${\gamma }^{*}={\gamma }^{\left[l-1\right]}+{\epsilon }_{\gamma },{\epsilon }_{\gamma }~N\left(0,{\sigma }_{\gamma }^2\right)$

${\gamma }^{\left[l-1\right]}$ 是l在 $l-1$ 步迭代时接受的值。通常，我们选择 ${\sigma }_{\gamma }^2$ 为对角矩阵，通过监测和调整对角线上的元素大小来保证接受率处在0.25~0.60之间。

2) 根据接受概率：

$p=\min \left\{1，\frac{f\left(\gamma \right)}{f\left(\left({\gamma }^{\left[l-1\right]}\right)\right)}\right\}>u,u\text{~U}\left(0,1\right)$

决定是否接受候选值 ${\gamma }^{*}$ 。否则，在第l步迭代时， ${\gamma }^{\left[l\right]}={\gamma }^{\left[l-1\right]}$ 。其中， $\text{U}\left(0,1\right)$ 表示 $0,1$ 之间的均匀分布。

4. 随机模拟

我们利用R软件进行随机模拟，基于Gibbs抽样和随机游走的M-H算法讨论参数估计效果，我们设定如下缓冲自回归模型：

$y_t=\{\begin{array}{c}0.3+0.8y_{t-1}+a_t,R_t=1\\ 0.4+0.7y_{t-1}+a_t,R_t=0\end{array}$

状态参数设定为：

$R_t=\{\begin{array}{ll}1\hfill & \text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}{y}_{t-d}\le 0.5\hfill \\ 0\hfill & y_{t-d}\ge 1.0\hfill \\ R_{t-1}\hfill & 其他\hfill \end{array}$

在模拟实验中，我们生成1500个观测值，并选择最后1000个观测值作为样本。我们在实验中运行MCMC迭代过程18,000次，根据每个参数的采样方案舍去样本产生的前9000个样本，取后面9000个作为有效样本。为了验证方法的稳定性，我们进行了两次模拟实验。最后缓冲自回归模型的随机模拟结果如下。

Table 1. Results of random simulation experiment

表1. 随机模拟实验结果

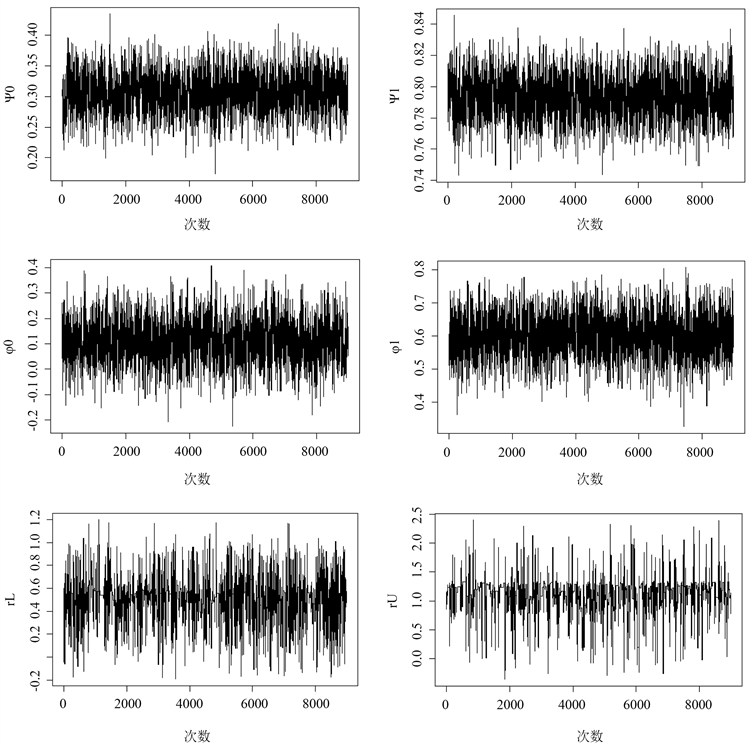
Figure 1. Trace plots of 9000 MCMC iterations of estimated parameters

图1. 9000次 MCMC迭代估计参数的轨迹图

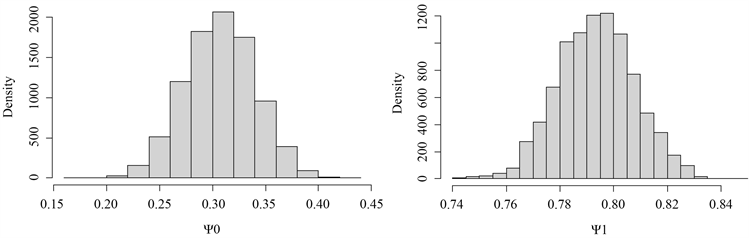
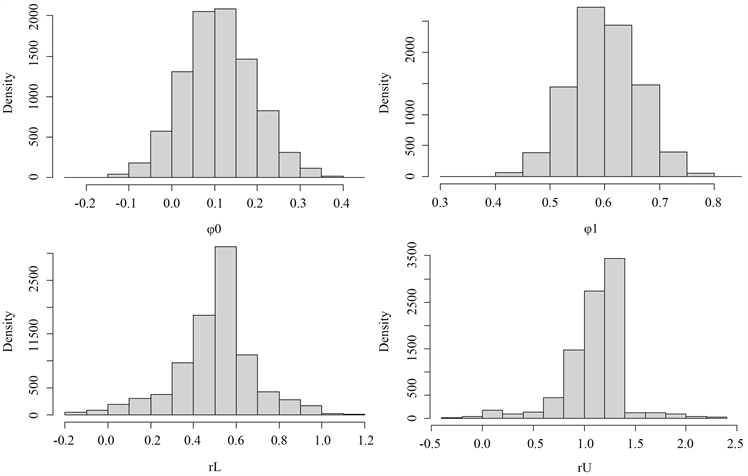
Figure 2. The histograms of the estimated parameters

图2. 参数频率分布直方图

当模型与真实情况下拟合度较高时，后验均值应与真实值十分接近。从表1的结果可以看出，缓冲自回归模型各个参数的后验均值与真值十分接近，并且每个参数的后验标准差也较小。同时，在95%的置信度下，参数的后验均值落在置信区间之中，可以看出结果是可靠的。在图1参数的迭代轨迹图与图2参数频率分布直方图也表明各参数迭代过程稳定、收敛的。依据以上的结果与分析，我们认为对缓冲自回归模型用MCMC抽样方案是有效的，随机模拟实验的结果较好。

5. 总结

本文在基于贝叶斯推断的基础上，得到缓冲自回归模型的条件后验分布，并结合MCMC抽样的方法对模型的参数进行估计。通过模拟实验表明，不仅模型的参数估计效果较为理想，还说明本文模型选择的后验概率估计是有效的。有了以上的实验结果依据，进一步，我们可以对模型的缓冲区进行非线性检验等。此外，在模拟实验的过程中，我们考虑到缓冲模型在预测均值、方差时的表现出来的优越性，因此，我们也可以将其应用在计算风险值方面。