1. 引言
随着电力信息物理系统(cyber physical system, CPS)的深度融合 [1] [2] [3] ,在实现电力系统整体运行性能最优化的同时,信息网络的安全漏洞也给电网带来潜在的威胁 [4] [5] 。虚假数据注入攻击(false data injection attacks, FDIA) [6] 作为通过篡改量测数据破坏电网信息完整性的攻击方式,具有较强的隐蔽性与干扰性,影响控制中心的决策分析 [7] [8] ,是对电力系统威胁程度较高的攻击方式之一。因此,建立有效的攻击检测机制对系统的安全稳定具有重要意义。
现有的FDIA检测方法主要分为空间相关型检测和时间相关型检测两类 [9] 。空间相关型检测通过传感器件间的关联关系进行交叉验证,达到检测目的,在实际操作中难度较大;时间相关型检测利用系统过去时间的状态预测未来的状态,根据状态预测方法的不同可分为:基于无迹卡尔曼滤波的动态状态估计检测方法 [10] [11] [12] 和基于短期状态预测的检测方法 [13] [14] 。
文献 [10] [11] 采用无迹卡尔曼滤波与最小二乘法同时状态估计,通过两者状态量的差别检测FDIA。文献 [12] 用无迹卡尔曼滤波状态估计与负荷预测以及潮流计算得到的状态量自适应混合预测,通过比较预测值与静态状态估计差值的分布检测攻击。但是基于UKF的动态估计检测方法预测步在状态量突变时效果不佳,需要通过量测值来修正,而被篡改量测将会导致检测偏差更大。文献 [13] 利用支持向量回归进行负荷预测,通过潮流计算得到的量测值与实际量测值的偏差来检测潜在的FDIA。与直接预测量测相比,该方法的计算成本减少了,但工作量仍然较大。文献 [14] 展示了一种基于深度神经网络的状态预测策略,通过计算估计状态与预测值之间偏差检测攻击。上述检测方法的攻击检测部分大多是比较状态预测值与静态估计值之间的距离指标判断状态量是否受攻击,而在实际电网中状态估计的结果直接影响决策,对实时性要求较高。
针对上述问题,本文基于改进ELM状态预测算法提出一种虚假数据注入攻击检测与定位的方法。本文主要工作如下:
1) 充分利用历史数据不受虚假数据影响的优势采用状态预测的方法,进而得到量测预测值,降低了模型的复杂度。此外,采用ELM算法学习速率和泛化能力较一般前馈神经网络更具有优势,更符合电力系统大数据的实时性需求。
2) 将电网拓扑结构与图论相结合,可以更直观清晰的了解量测的异常情况,对判断攻击起了重要作用。
3) 利用节点强度判断是否受到攻击,检测攻击的同时可以定位到节点,在实践中识别攻击位置对快速部署有效策略至关重要。
2. 问题描述
2.1. 状态估计
电力系统状态估计是通过各种智能仪表的监测数据,对当前系统运行状态评估的过程。其结果常用于经济调度、安全评估等。
在交流潮流模型中,非线性关系可表示为:
(1)
式中:
为状态变量,n是状态变量的数量,
为智能监测仪表的量测,m是量测的数量,
为量测与状态的非线性关系,
为量测误差,服从均值为0的高斯分布。
实际系统中各节点的电压幅值
和相角
为状态量,节点注入有功功率
、无功功率
和线路上有功
和无功功率
为测量值,关系如下:
(2)
(3)
(4)
(5)
式中:
、
分别为节点i、节点j的电压幅值;
节点i与节点j的电压相角差;
、
分别为节点i与节点j之间支路电导、电纳。
通常交流状态估计可以描述为一个二次优化问题,目标函数取得最小时的状态量即为最优估计。
(6)
式中:W为权重矩阵。
2.2. 智能电网虚假数据注入攻击
由于测量误差和通信的不稳定,传输数据偏离原有的真实值,为了确保状态估计结果的准确性,基于残差分析的传统坏数据检测器需要对不良数据检测和辨识。通过异常数据与正常数据的残差分析,误差超过阈值即判定为攻击数据 [7] 。假设量测变化为a,引起状态量变化c,此时残差表示为:
(7)
式中:
和
分别表示有无攻击时的残差值,
表示残差增量,由公式(7),当
(8)
残差增量为0,受到攻击时未引起残差的变化,当前系统无法检测到恶性数据 [15] ,FDIA成功绕过不良数据检测。
由上述虚假数据注入原理,攻击者将虚假数据注入AC状态估计通常有两种方法:操纵系统状态变量和操纵特定的测量。根据功率平衡方程(2)~(5),如果攻击者以状态变量为目标,依赖于该状态变量的所有量测都将受到影响。因此,一般是通过注入攻击篡改测值来达到改变状态量的目的。
3. 状态预测模型
3.1. 状态预测
极限学习机算法是由Huang等 [16] 提出的一种单层前馈神经网络学习算法,是对传统基于梯度前馈神经网络的改进,提升了学习效率并简化参数的设定。ELM仅需要求解输出权重,是一个线性参数模型,学习过程易于在全局极小值处收敛,因此训练速度快,抗干扰能力强,在解决复杂问题上具有一定的优越性 [17] 。
极限学习机的组成包括输入层、隐含层和输出层,结构如下图1所示。
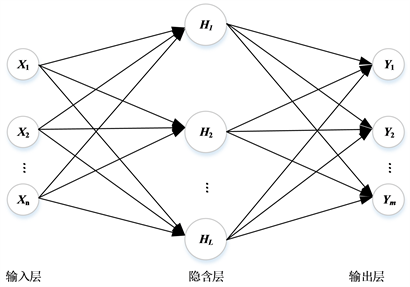
Figure 1. Network structure of the Extreme Learning Machine
图1. 极限学习机的网络结构
给定一个包含N个不同数据样本
,R为实数,ELM回归模型为:
(9)
式中:
为输入层与隐含层的权重;
为隐含层与输出层的权重;
为隐含层的偏置;L为隐含层的节点数;
为隐含层的输出;
为隐含层的无限可微的激活函数,文中取Sigmoid函数。
隐含层输出矩阵为:
(10)
在确定了权重w和隐含神经元阈值b之后,可求得隐藏层的输出矩阵H,ELM训练的过程等价求解线性方程
的最小二乘解,目标函数为:
(11)
其中,期望矩阵为
(12)
解为
,其中
为H的Moore-Penrose广义逆。
3.2. 参数优化
由前文可知,ELM的初始权值和阈值都是随机产生的,每次产生都具有盲目性,本文利用麻雀搜索算法 [18] 对初始权值和阈值进行优化。
麻雀搜索算法(sparrow search algorithm, SSA)是2020年由Xue等 [18] 提出的一种群智能优化算法,具有寻优能力强、收敛速度快的特点。将麻雀群体分为发现者、加入者和预警者3部分,种群中适应值较高的作为发现者,负责寻找食物并为加入者提供觅食的方向。在每次迭代过程中,发现者位置按照如下公式更新:
(13)
式中:t表示当前迭代次数,
表示第i个麻雀种群在第j维中的位置信息,
为
之间随机数,
表示最大迭代次数,Q为服从正态分布的随机数,L是一个1 × d并且元素全是1的矩阵,
分别表示麻雀种群位置的预警值和安全值。
在觅食过程中,部分加入者会监视发现者,对其食物掠夺提高自己的适应度,从而成为发现者,加入位置按照下式更新:
(14)
式中:
表示当前发现者所发现的最优位置,
表示当前全局最差的位置,A表示其元素随机幅值为1或−1的1 × d的多维矩阵。
在麻雀种群中,意识到危险的麻雀数量占总数的10%~20%,随机产生位置,按照以下公式更新:
(15)
式中:
是全局最优位置的个体,β服从标准正态分布的随机数用来作为步长控制参数,
表示当前麻雀个体i的适应度值,
,
分别表示全局最佳适应值和最差适应值,ε > 0,一般设为10‒8,
用来控制麻雀运动方向(图2)。
使用均方根误差作为预测精度评判标准
(16)
适应度函数选取训练后的均方根误差,值越小,表明预测的数据与原始数据重合度越高,最终优化的输出为最佳初始权值和阈值,再利用最佳权值和阈值训练的网络对测试数据集测试。
3.3. 检测与定位
由历史数据不受虚假数据攻击的影响,采用SSA-ELM算法对状态变量预测,结合网络拓扑结构和参数得到预测量测值,与系统量测仪表传输的数值比较,得出离群值,这里采用“3σ”准则,即几乎所有变量的观测值都应该在观测值平均值的3σ距离之内。因此,任何位于该距离之外的观测值都可以被认定为异常值。

Figure 2. SSA-ELM algorithm framework
图2. SSA-ELM算法流程图
(17)
电网实际上包含了两类拓扑结构:几何拓扑和物理拓扑。前者反映了电网设备的几何连接状态,后者体现电网元件物理上的电气耦合 [19] 。电力系统的拓扑可以用图
,E(G)>来表示,其中V(G)为图G中包含的节点集合,E(G)为图G中包含的边集合 [20] 。
异常值的分布可以间接反映攻击的目标,针对筛选出来的异常值根据以下规则创建图:
1) 将量测分为两组:
A组:电压幅值Ui、相角θi和节点注入有功功率Pi、无功功率Qi;
B组:线路有功潮流Pij和无功潮流Qij;
2) 自边:各节点如果检测到至少一种A组类型的变量为异常,则将此节点添加到图中,用一条边连接到自身,并指定该边的权重为向量中A类型变量数量的一半,如图3(b);
3) 互边:如果检测到B类型的变量为异常值,则将代表此线路的两个端点添加到图中,用一条边连接这两个节点,并将该边的权重指定为B类型变量的数量,如图3(c)。
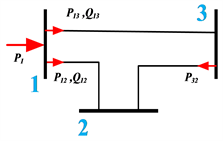 (a)
(a) 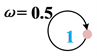 (b)
(b) 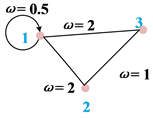 (c)
(c)
Figure 3. Schematic diagram of weighting map generation
图3. 权重图生成示意图
创建图后,使用节点强度的概念衡量每个节点的重要性,图中一个节点的阶数简单的定义为直接连接到该节点的边数。这一定义在 [21] 中被推广到考虑加权强度si的加权图中的边的权重,定义如下:
(18)
式中:
是图邻接矩阵的第(i, j)个元素,
是分配给连接节点i和节点j的边的权重。
计算图中每个节点的si后,将根据以下规则最终决定向量z中检测到的异常值是否由网络攻击引起:如果图中至少可调数量的节点的si值大于预定义的阈值ξ,则检测并定位攻击(图4)。
(19)

Figure 4. Block diagram of false data detection model
图4. 虚假数据检测模型框图
4. 算例分析
4.1. 测试系统
本文测试系统中使用的负载数据来自纽约电力管理局公布的电力负荷数据(New York independent system operator, NYISO) [22] 。参考文献 [23] 将NYISO数据中如图5所示的11个负荷区域分别接入IEEE-14节点系统,该负荷数据的记录间隔为5分钟,图6为CAPITL区某三日符合波动情况。IEEE-14节点测试系统的量测值和状态变量的5分钟间隔数据生成程序步骤如下:
Figure 5. Map of actual electricity areas in 11 New York states
图5. 纽约11州实际电力区域图
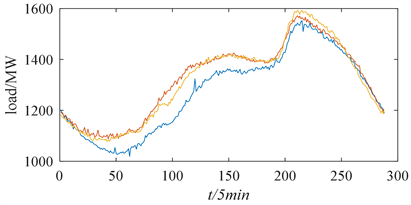
Figure 6. Daily load curve for the first 3 days of the CAPITL region in 2016
图6. 2016年CAPITL区域前3天的日负荷曲线
1) 将每个NYISO电网区域连接到IEEE14节点测试系统中的11条负荷总线之一,对应关系如下表1;
2) 初始化IEEE-14节点有功负荷,基于各节点功率因数恒定的前提,算出对应的无功功率;
3) 累加新的负荷有功功率和无功功率,计算新的总有功和无功与相应初始值的比率,按比例增加每个发电机的发电量;
4) 每5分钟的时间间隔,在IEEE14节点系统上运行基于MATPOWER软件包,得到各节点每个时刻的电压相量值,并将其存储在历史数据库中。
4.2. 单节点攻击检测
根据初始节点和支路信息,运行潮流计算得到14个节点电压幅值和电压相角共27个系统状态值,其中1节点为平衡节点。
根据公式(2)~(5)得到系统的量测值,包括节点有功注入和无功注入,以及20条线路的有功功率和无功功率。通过每五分钟的实际负荷数据得到68个量测值,支路量测值如附录图A2所示。
假设电网在11月运行良好,在12月遭到攻击。从网络中采集了8640组正常样本。将11月份收集的数据按照9:1划分为训练集和测试集,初始种群数设置为20,搜索最优神经元范围是1~100,迭代次数大于100时寻优过程结束,对电压预测分析如下表2,其中节点14电压相角和适应性曲线如图7。

Table 2. IEEE-14 system voltage phase angle root-mean-square absolute error analysis
表2. IEEE-14系统电压相角均方根绝对误差分析
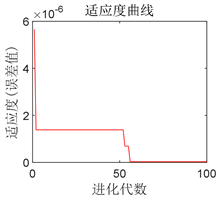
Figure 7. 14-node voltage phase angle prediction and its adaptability curve
图7. 14节点电压相角预测及其适应性曲线
在系统正常运行条件下,可以得到当前系统量测的近似真实值,攻击者在原始量测上强加的扰动将使被攻击量测值远离实际值。
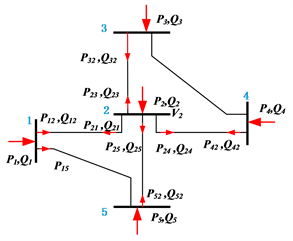
如下图8所示,2节点注入1.1倍原始电压相角值的攻击,检测到的异常值包含支路1-2、2-3、2-4和2-5两端的有功功率和无功功率,节点1-2-3-4-5注入的有功功率和无功功率,以及节点2的电压相角,节点2异常分布图生成过程如图9所示;针对节点14电压幅值的1.1倍原始值攻击确定的异常值包括支路9-14和13-14两端的有功功率和无功功率,节点9、13和14注入有功和无功功率,以及节点14的电压幅值。
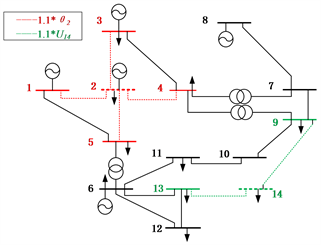
Figure 8. IEEE14 test system attack schematic
图8. IEEE-14测试系统攻击示意图
 (a)
(a) 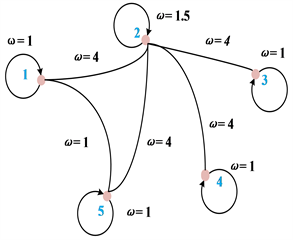 (b)
(b)
Figure 9. Node 2 outlier distribution weight map
图9. 节点2异常值分布权重图
由检测结果表3和表4可以得出,这两种攻击将通过所提出方法检测和定位,因为他们各自的图形中至少包含一个强度为10或者更高的节点,如图10、图11所示。

Table 3. 1.1*θ2 attack detection results
表3. 1.1*θ2攻击检测结果

Table 4. 1.1*U14 attack detection results
表4. 1.1*U14攻击检测结果
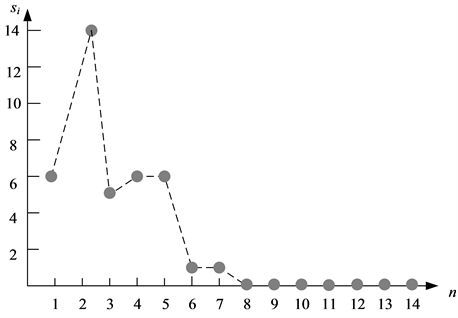
Figure 10. Node 2 attack detection strength map
图10. 节点2攻击检测强度图
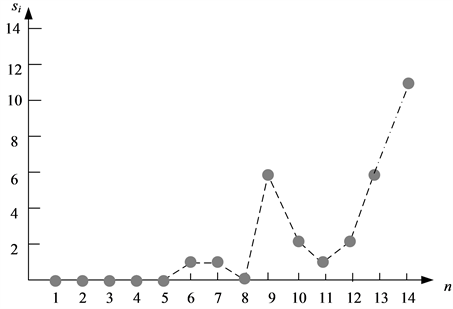
Figure 11. Node14attack detection strength map
图11. 节点14攻击检测强度图
4.3. 全覆盖检测
为验证所用检测模型,对IEEE-14节点每个状态变量模拟攻击,在原始值上改变相应的比例,表5为检测结果。
本文采取五种攻击模式,对27个状态量模拟虚假数据注入攻击,攻击幅度分别为原始状态值的90%、95%、100%、105%、110%,其中100%代表状态值未遭受攻击。ND为节点强度在阈值以上的被检测样本的个数,ND%为ND的百分数。采用当下攻击时刻前的288组数据,即样本总数据。
由原始值90%和110%的数据可知,当状态变量改变较大时,本文检测方法可以很好地检测到虚假数据的攻击;由原始值95%和105%的攻击数据可知,状态变量改变较小时,ND会有所增加,这是因为其状态变量更加接近原始值,但是本文检测方法均有效检测到虚假数据的注入攻击。由于不同节点的强相关量测数目不一样,在相同攻击情况下,ND%会有所不同,如节点8等,由于其出线度仅为1,即强相关量测较少,导致部分样本数据的关联度在阈值之上。

Table 5. False data injection attacks test results
表5. 虚假数据注入攻击检测结果
5. 结论
虚假数据的注入对电网的稳定性运行带来了巨大威胁,传统的不良数据检测无法判别。本文通过状态预测结合异常分布图在IEEE-14节点测试系统进行了仿真分析,提出了一种离线预测,在线检测的攻击检测方法,利用攻击前后的异常值分布求得节点强度变化来判断是否收到攻击,对单节点多节点进行实验证明模型的有效性。