粗糙带圆柱尾迹流场中翼型噪声的数值研究

Airfoil in Rough Cylindrical Wake Flow Field Numerical Study of Noise

摘要: 通过数值模拟方法研究了不同高度粗糙带圆柱下尾迹变化，以及粗糙带对圆柱和翼型的气动性能和噪声的影响。高粗糙带下的圆柱升阻力系数更大，低粗糙带则影响较小，粗糙带对翼型的升阻力系数影响较小，高粗糙带在一定区域会提高翼型的表面时间平均压力系数。并且高粗糙带会改变圆柱表面的边界层分离后的流动和低速回流区的范围，增强扰动影响后方翼型流场。FW-H方程积分不同表面得到远场位置声压级，在90˚位置高粗糙带会增加圆柱和翼型噪声，在60˚位置积分面只有翼型时，高粗糙带圆柱后方翼型的噪声反而更小。还比较了局部流场和全局流场的压力脉动均方根值，表明高粗糙带圆柱后方流场有更强的声源强度，最后分析了瞬时涡结构和湍流强度的变化，表明高粗糙带对后方尾迹具体扰动。

Abstract: The change of wake under the cylinder with different height rough band and the influence of rough band on the aerodynamic performance and noise of the cylinder and airfoil are studied by numeri-cal simulation. The cylindrical drag coefficient under the high rough zone is greater, while the low rough zone has little influence on the drag coefficient of the airfoil. The high rough zone will increase the surface time average pressure coefficient of the airfoil in a certain area. In addition, the high roughness zone will change the flow range after boundary layer separation on the cylindrical sur-face and the low velocity reflux zone, and enhance the disturbance influence on the rear airfoil flow field. FW-H equation is integrated with different surfaces to obtain sound pressure levels at far-field positions. The noise of cylinder and airfoil is increased at 90˚ with high roughness band, but the noise of airfoil behind the cylinder with high roughness band is smaller at 60˚ with only airfoil as integral surface. The root mean square value of pressure pulsation of local and global flow fields is also compared, indicating that the flow field behind the cylinder with high rough zone has stronger sound source intensity. Finally, the changes of instantaneous vortex structure and turbulence in-tensity are analyzed, indicating that the high rough zone has specific disturbance to the rear wake.

1. 引言

来流湍流与下游转子的相互作用是产生噪声的重要来源，这也是在海洋、飞行器、汽车、船舶和透平等领域的推进器设计过程中需要重点关注的问题 [1] [2] 。来流湍流可由绕流上游复杂结构(如静子、复杂曲面)的边界层和尾迹产生，其一般具有非均匀各向异性特征，包含非常宽泛的时空多尺度结构。上游大尺度的相干结构与下游转子相互作用会产生tonalnoise。小尺度的涡结构与转子相互作用，会引起转子边界层涡沿着流向输运、分离和脱落，从而产生宽频湍流噪声。因此，分析来流湍流与下游结构的相互作用，研究压力脉动和噪声产生的机制，具有重要的理论和实践意义。

转子噪声是一个经典声学问题，学者们在实验和数值上均开展了较多研究。大量的关于格栅湍流下游转子噪声的实验 [3] [4] [5] [6] [7] 丰富了人们对转子噪声的认识，也为数值模拟提供了依据。而在数值上常用FW-H方程预测远场噪声。如：Wang和Moin [8] 采用大涡模拟计算了翼型后缘的边界层流动，得到的远场声与试验测量保持一致。Eltaweel和Wang [9] 用边界元法与大涡模拟相结合，研究了NACA 0012翼型与上游圆柱在低马赫数下的湍流尾迹相互作用产生的噪声，付建等 [10] 对比了LES和DES在计算流体动力噪声中的适用性。

大量研究表明圆柱绕流产生的尾迹对下游翼型的冲击会产生严重的干涉噪声，而在实际圆柱绕流中会产生涡激振动(VIV)现象，VIV在许多工程分支中是一个持续存在的问题，并且对于各类水下工程中使用的立管来说可能特别严重 [11] 。目前有许多VIV抑制方法以提高结构安全性，其分类为：a) 控制降低的速度，b) 控制质量和阻尼，以及c) 控制涡流脱落 [12] [13] 。被动控制方法用于控制涡流脱落或结构周围的流动。它们广泛用于VIV抑制 [14] [15] [16] [17] 。Bernitsas和Raghavan [18] 以选择性表面粗糙度的方法来加强圆柱的振动，进而增大能量输出，并且取得了良好的效果。Chang等 [19] 关于对称粗糙带圆柱的流致振动做了大量研究，得到了不同规格对称粗糙带下的振幅及功率等数据。在圆柱表面设置粗糙带是一种常用的被动控制方法。对于在粗糙带圆柱下游的翼型噪声的研究目前较少，因此在该方面展开研究。

本文采用前方圆柱、后方翼型的简化模型，采用不可压缩LES和FW-H声比拟相结合的数值分析方法，试图探究同一位置两种不同高度的粗糙带对圆柱尾迹的影响，进一步分析对下游翼型的气动性能和噪声性能的影响。

2. 数值计算方法

2.1. 计算域和边界条件以及计算模型

图1显示了本次模拟的计算以及相应的边界条件，计算域在流向，横向，和展向的长度分别为16C、10C和0.24C。假定本文考察的流体介质为不可压水，来流速度为3 m/s，假设翼型攻角为0˚，雷诺数 $R{e}_c=2.98\times {10}^5$ 。Nicoud [20] 提出了一种新的基于速度梯度张量平方的亚网格尺度模型-WALE模型，该模型具有很好的复杂几何适应性，且计算量较小，因此本文拟采用此模型进行大涡模拟计算。在采用ANSYS Fluent 22.1软件的模拟中，N-S方程采用的压力–速度耦合方式为SIMPLE算法，压力的空间离散为二阶精度，时间推进采用bounded二阶隐式格式。入口、上下边界给定速度边界条件，出口给定压力边界条件，展向给定周期边界，壁面默认无滑移条件。声学采样的时间步长参考 [21] 设置为 $t=1\times {10}^{-5}\text{s}$ ，较小的时间步长确保能够得到精确的流场。计算过程先使用RANS得到稳态流场，在稳态流场的基础上再进行LES模拟，在流场周期稳定后，耦合FW-H声比拟模型得到远场的噪声，声学采样时间步数为20,000步，大约为圆柱脱落周期的7倍，保证足够长的流动时间以获取远场噪声低频特征。

计算的几何模型如图2所示，计算模型由光滑圆柱与两个不同高度粗糙带圆柱加后方NACA0012翼型组成。两个粗糙带的位置离前驻点75˚，小于圆柱分离点，无量纲高度分别为 $Y^{+}\approx 1.9$ 和 $Y^{+}\approx 13$ ，分别位于边界层粘性底层和过渡区。

Figure 1. Computation domain and boundary conditions

图1. 计算域及边界条件

(a) smooth(b) low thickness (c) high thickness

Figure 2. Sketch of different cylindrical roughness strips

图2. 不同圆柱粗糙带示意图

2.2. 网格划分

为了提高网格质量和正交性，提高收敛速度，采用基于O型拓扑的全六面体结构化网格策略，并在圆柱和翼型周围区域布置足够高分辨率的网格以精细捕捉周围流场结构，在远场区域采用较稀疏的网格以降低计算成本。图3显示了整体计算区域、圆柱和翼型表面局部网格分布。其中，圆柱表面分布了280个网格，翼型表面分布了540个网格。总体的网格数量为 $4.61\times {10}^6$ ，展向网格数量为42个。圆柱和翼型表面第一层网格 $Y^{+}$ 都小于1，以满足LES模型计算对网格的要求。

2.3. 计算方法验证

由于水下噪声与气动噪声的预测方法基本相同，故采用了Jacob [22] 等人关于圆柱与翼型干涉噪声的经典试验为参考，并将计算结果与试验数据进行对比，以验证CFD与声比拟相结合方法的准确性。计算案例设置如下，NACA0012翼型弦长C = 100 mm，圆柱直径d = 0.1 C，圆柱中心与翼型前缘距离为1.05C，展向长度L = 0.35 C，来流速度为72 m/s。

Figure 3. Schematic diagram of mesh

图3. 网格示意图

使用LES联合声比拟FW-H方法计算出远场点的声数据，并与Jacob的试验结果和模拟结果进行对比。图4给出了远场监测点位于Z = 0平面的位置，每隔6˚布置一个检测点，共有31个远场监测点。

Figure 4. The far-field sound pressure receiving point around the wing

图4. 机翼周围的远场声压接收点

图5为90˚监测点声压级对比。可见，本文的计算结果与已发表文章中的试验结果和模拟结果无论是宽频噪声趋势上还是主频及其峰值都比较吻合。由图6可以看出声远场的指向性也与试验吻合，从而证明了目前的计算方法在一定的精度范围内是可行的，因此在后续的计算中也采用LES联合声比拟FW-H方法计算水下噪声。

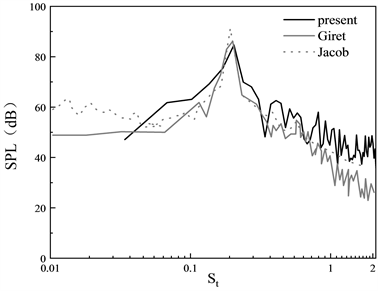
Figure 5. 90˚ far-field sound pressure level

图5. 90˚远场声压级

Figure 6. Far field sound pressure directivity

图6. 远场声压指向性

3. 结果与讨论

3.1. 气动性能

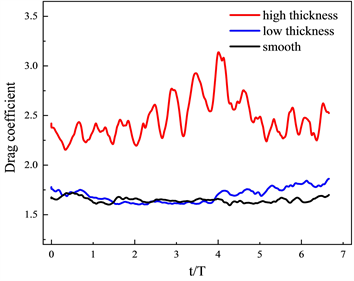
为了研究粗糙带圆柱对翼型的水动力性能的影响，图7为不同高度粗糙带圆柱的升力系数 $C_L=\frac{F_L}{\frac{1}{2}\rho V_{\infty }^{2}S}$ 和阻力系数 $C_D=\frac{F_D}{\frac{1}{2}\rho V_{\infty }^{2}S}$ 在多个周期内的时域波动。由图7(a)可见，高粗糙带圆柱阻力系数脉动幅值明显大于光滑粗糙带和低粗糙带，这是因为高度处于过渡区的粗糙带结构改变了圆柱光滑度阻碍了来流，而高度处于粘性底层的粗糙带对圆柱阻力系数影响不大。

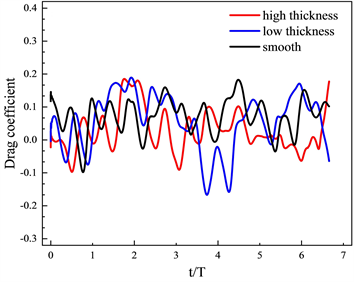
同时图7(b)可见高粗糙带圆柱的升力系数脉动幅值变化与阻力系数相似，这是由于粗糙带影响了圆柱表面压力脉动，预期会导致圆柱偶极子声源增强，从而加强噪声。此外不同圆柱后方的翼型阻力系数和升力系数变化如图8所示，在图中并未看到明显差异性。进一步取翼型上表面与展向位置Z = 0截面交线，研究粗糙带对翼型表面时间平均压力系数 $C_p$ 的影响。在图9中，发现当0.04 < x/c < 0.6时，高粗糙带圆柱后方的翼型的压力系数更高，在其他位置区别不大。

图10为圆柱附近Z = 0截面的时间平均X方向速度分布。观察前圆柱周围流场，发现高粗糙带圆柱的边界层被破坏，并且对于边界层分离后的流动有较大影响，这是因为更高的粗糙带导致更大的扰动，同时引起低速回流区的变化。

(a) (b)

Figure 7. Drag coefficient of the cylinder

图7. 不同圆柱的升阻力系数

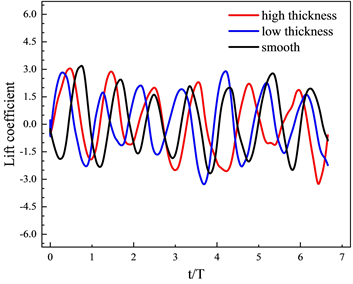(a) (b)

Figure 8. Drag coefficient of the airfoils

图8. 不同翼型的升阻力系数

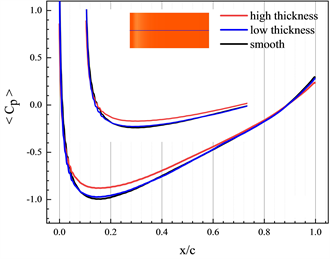
Figure 9. Time-averaged pressure coefficient

图9. 时间平均压力系数

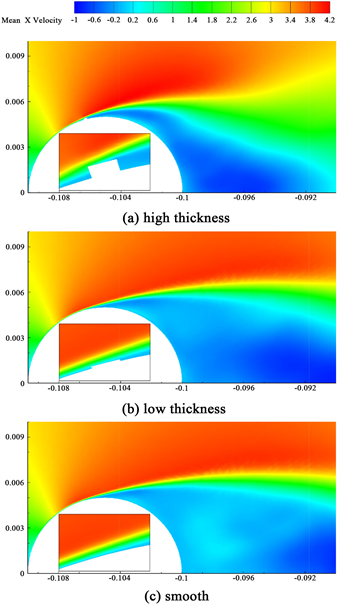
Figure 10. Average velocity cloud in X-direction for Z = 0 planes

图10. Z = 0截面时均X方向云图

图11为主流区域Z = 0截面时间平均X方向速度分布，低速回流区的变化可以更加明显的看到，更高的粗糙带圆柱后面的有一个更短距离的低速回流区。在尾迹区域和翼型附近的流体速度也更大。

3.2. 声学性能

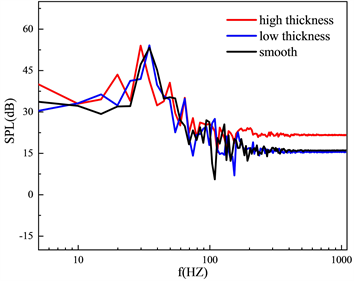
声学计算结果是对圆柱和翼型表面积分得到的。由于考察的是低速流动，因此可以取圆柱和翼型表面作为声源，通过FW-H方程积分固壁得到远场点的声压，经过快速傅里叶变换(FFT)得到远场点的声压级谱 $SPL\left(f\right)=10\log \left(S_{pp}\left(f\right)/p_{ref}^2\right)$ ，其中 $p_{ref}=2\times {10}^{-5}\left(\text{Pa}\right)$ ，监测点的位置如图4所示，分别取90˚和60˚两点的声压级比较不同情况下的声学性能。图12为圆柱加翼型表面积分得到的远场声压级频谱，在两个角度的监控下均可以发现主频位置的差异。

更高的粗糙带圆柱带来主峰的频率偏移，表明相较于低粗糙带圆柱和光滑圆柱，高粗糙带影响了圆柱的尾涡脱落频率。在90˚位置频率更高时高粗糙带圆柱加翼型的声压级更高，另外两种情况的声压级基本相同。在60˚位置则是低粗糙带圆柱加翼型的声压级最高。可以看出在不同远场位置的声压级并不相同。为了进一步探究单一壁面的声压级变化，图13为积分面只有圆柱的远场声压级，在两个角度下，无论是低频还是高频高粗糙带圆柱的声压级都更高，主频位置的频率也更小，在两个角度下三个圆柱的趋势是一样的，更高的粗糙带对声压级影响较大，低粗糙带的影响不明显。

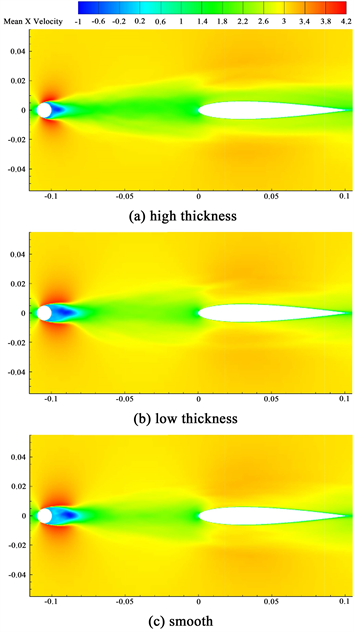
Figure 11. Average velocity cloud in X-direction for Z = 0 planes

图11. Z = 0截面时均X方向云图

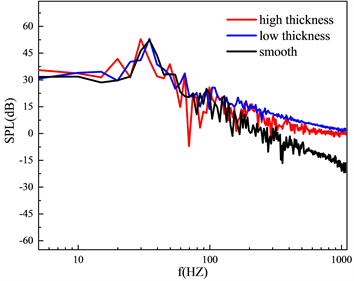(a) 90˚ (b) 60˚

Figure 12. Far-field sound pressure level at different monitoring points

图12. 不同角度的声压级

(a) 90˚ (b) 60˚

Figure 13. Far-field sound pressure level at different monitoring points

图13. 不同角度的声压级

(a) 90˚ 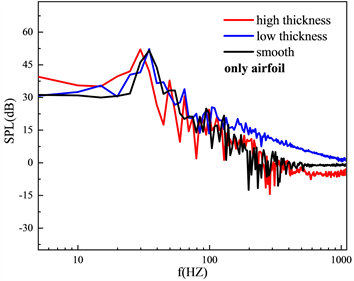(b) 60˚

Figure 14. Far-field sound pressure level at different monitoring points

图14. 不同角度的声压级

3.3. 机理分析

为了分析噪声增强的机理，本节将从脉动流场的角度进行详细的对比分析。

引入方程 ${p^{\prime }}_{rms}=\sqrt{\mathrm{var}\left(p^{\prime }\left(z_1,t\right)\right)}$ 给出的压力脉动均方根(RMS)值来评价声源，因为它在一定程度上

反映了声音的产生和传播 [23] ，其中 $p^{\prime }=p-p_0$ ，其中 $p$ 为瞬态压力， $p_0$ 为时间平均瞬态压力，var为瞬态压力信号在一系列时间内的方差。Z = 0截面局部流场和全局流场的 ${p^{\prime }}_{rms}$ 分布如图15和图16所示。图15中高粗糙带圆柱表面附近流场的均方根值较高，而其它两个圆柱的压力脉动均方根值都较小。这是因为高粗糙带的强扰动导致的，强扰动在平均X方向速度场中也能看到。图16中全局压力脉动均方根值也可以看到高粗糙带圆柱后方流场的压力脉动均方根值更高，这意味着高粗糙带圆柱后方流场有更高的声源，低粗糙带圆柱和光滑圆柱后方的声源基本相似，这与90˚远场声压级相对应。

涡流结构的演化规律是探讨噪声抑制机理的重要手段。图17显示了用y速度着色的瞬时等值面 $Q=50000{\text{s}}^{-2}$ 。可以看出在不同圆柱后方翼型附近的瞬时涡结构，前缘涡在到达前缘之后破碎为上下

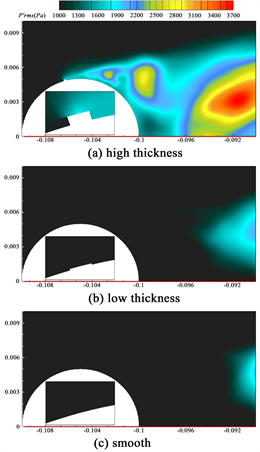
Figure 15. Root mean square value of pressure pulsation for Z = 0 planes

图15. Z = 0截面压力脉动均方根值

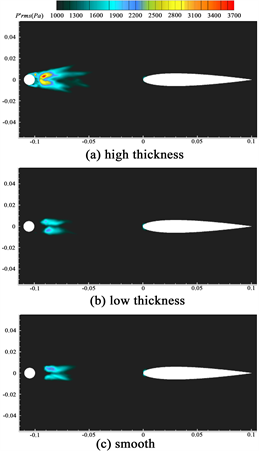
Figure 16. Root mean square value of pressure pulsation for Z = 0 planes

图16. Z = 0截面压力脉动均方根值

表面附近的细小涡结构，随着尾迹的周期性撞击，交替的y方向速度表明在上下表面存在表面涡的附着，卷起和脱落。在高粗糙带圆柱后方翼型附近的涡结构更加密集，说明高粗糙带圆柱尾迹更加复杂，表面细碎的涡结构将导致翼型表面更强的压力脉动，因此远场90˚位置的翼型气动噪声更强。

Figure 17. Transient vortex structures with isosurface Q = 50000 S⁻², colored with y-velocity

图17. 瞬态涡旋结构等值面Q = 50000 S⁻²，用y方向速度着色

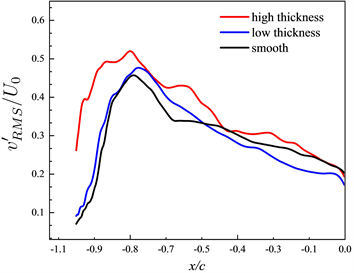
湍流波动的强度由湍流强度(TI)反映，定义为 $T_u=\frac{1}{U_o}{u^{\prime }}_{RMS}$ 图18为X轴上翼型前方线段上两个方向

的湍流强度，高粗糙带后方前半部分线段上x方向的湍流强度明显更大，在靠近翼型的位置也可以观察到。同时y方向的湍流强度也会整体增大。

(a) ${u^{\prime }}_{RMS}/U_o$ (b) ${v^{\prime }}_{RMS}/U_o$

Figure 18. Turbulence intensity on the forward segment of the airfoil

图18. 翼型前方线段上的湍流强度

4. 结论

1) 更高的粗糙带对圆柱的时域升力系数和阻力系数影响更大，所有高度粗糙带对后方翼型的升阻力系数影响不大，并且高粗糙带对后方翼型的时间平均压力系数有增强作用，同时圆柱后方低速回流区的大小改变，翼型附近的流速增强。

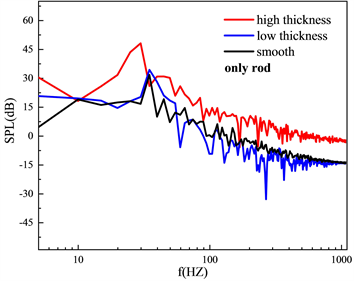
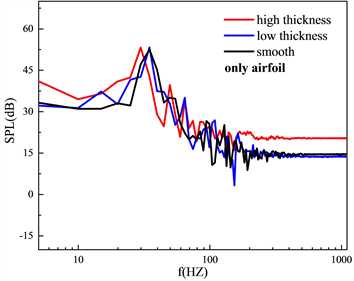
2) 通过积分不同壁面比较远场声压级的变化，积分所有壁面时，高粗糙带圆柱会影响远场声压级的主峰的频率和大小，90˚和60˚的位置频谱的变化趋势不一样。积分圆柱壁面时，高粗糙带圆柱会影响主峰频率，增加低频和高频噪声，两个位置的声压级变化趋势一样。积分翼型壁面时，90˚位置和积分所有壁面情况基本相同，60˚位置高粗糙带圆柱后方翼型声压级反而最低。

3) 通过比较不同流场的压力脉动均方根值来反映声源强度，发现高粗糙带导致的强扰动会使圆柱后方流场声源强度增高，翼型周围流场瞬时涡结构和后方线段上的来流湍流强度都表明高粗糙带圆柱对尾迹的影响，从而导致更高的声压级。

总体而言，更高的粗糙带会影响圆柱附近和后方流场，增强扰动，一方面改变了圆柱自身的噪声，另一方面改变边界层分离后的流场形态，导致撞击翼型的噪声发生改变。