基于粒子群算法的电机公差优化设计

Motor Tolerance Optimization Design Based on Particle Swarm Optimization Algorithm

摘要: 为了提高电机的装配质量和降低总成本，需对形成电机定、转子间气隙的关键零部件组成环公差进行优化设计。以加工成本和产品质量损失成本为目标函数，以其功能要求和经济加工能力为约束条件，建立了多目标多约束的电机公差优化模型。采用多目标粒子群优化算法，得到了在电机总成本最低的情况下各个关键组成环的公差，并通过3 DCS进行仿真验证。研究结果表明采用优化后的设计公差值，电机装配成功率提升了约11.92%，总成本下降了约24.29%。

Abstract: In order to improve the assembly quality of the motor and reduce the total cost, it is necessary to optimize the ring tolerance of the key components that form the air gap between the stator and ro-tor of the motor. With the machining cost and product quality loss cost as the objective function, the tolerance of the key component ring as the design variable, and the functional requirements and economic machining capacity as the constraint conditions, a multi-objective and multi- constraint tolerance optimization model of motor was established. By using multi-objective particle swarm op-timization algorithm, the tolerances of each key component ring with the lowest total motor cost were obtained, and the simulation was verified by 3 DCS. The results show that the success rate of motor assembly increases by 11.92% and the total cost decreases by 24.29% with the optimized design tolerance value.

1. 引言

电机是保证设备正常运转的核心动力部件。电机装配后定转子之间形成的气隙是决定电机性能和装配质量的重要因素。随着电机性能的不断提升，对影响气隙变动范围的装配尺寸链进行公差建模和分析的需求越来越多，且对分析精度的要求也越来越高。

公差设计是保障产品设计质量的关键，其公差设计的好坏直接关系到电机产品的质量与成本。通常零件加工成本与设计公差成反比，设计公差越小，加工精度越高，但加工成本也越高。因此，需要对电机产品进行合理的公差设计，在提高产品质量，满足功能要求的同时还能降低电机的加工成本。

当前国内外公差优化设计的研究主要集中在建立合理的公差优化设计模型和选择高效的求解算法两个方面 [1] [2] 。谢雄伟等 [3] 运用了遗传算法优化设计RV减速器各零件的关键尺寸公差，并运用Adams软件进行回差仿真验证。程彬彬等 [4] 基于产品退化方式给出了公差与产品服役寿命密度分布函数的关系，建立了综合考虑产品平均服役寿命、加工成本及质量损失的公差优化数学模型。钱鹏等 [5] 以某车窗升降系统的三维装配公差分析为例，以公差收严的收益比为评价因素，实现了考虑柔性变形的车窗升降系统公差优化设计。传统求解多目标优化问题往往是通过一定的策略为多种目标函数配以固定的权重系数，将多目标问题转化为单目标问题后进行求解，计算时常常陷入局部最优，导致这些传统的优化算法很难找到使多个目标函数同时取得最优的解。张康锋 [6] 构建了基于加工成本和质量损失的公差分配多目标优化数学模型，采用基于Pareto机制的快速非支配排序遗传算法，得到了多装配尺寸链组的公差优化分配方案。

本文以某型号电机产品为研究对象，以电机的加工成本和质量损失成本作为目标函数，以各零件组成环公差为设计变量，建立电机产品装配公差数学模型，基于多目标粒子群算法，对电机各零件的公差进行优化，以得到兼顾产品成本、质量、装配成功率的最优公差分配方案。

2. 公差多目标优化模型的建立

2.1. 加工成本模型

零件的加工特征一般分为四类，分别为外圆特征、平面特征、内孔特征、定位特征。不同加工特征所需要的加工成本大小各不相同 [7] 。我国制造加工类企业在进行批量生产时，结合零件的加工尺寸特征代表，采用了线性和指数复合的成本公差模型 [8] 。不同零件加工特征的成本–公差模型如下：

1) 内孔尺寸特征的成本–公差数学函数为：

$C\left(T\right)=12.6691{\text{e}}^{-37.5279T}+2.486{\text{e}}^{\frac{0.000978}{T}}$ (1)

2) 外圆尺寸特征的成本–公差数学函数为：

$C\left(T\right)=\{\begin{array}{l}15.113{\text{e}}^{-42.2874T}+\frac{T}{0.8611T+0.01508}\left(T\le 0.11\right)\\ 1.273338\left(T>0.11\right)\end{array}$ (2)

3) 平面尺寸特征的成本–公差数学函数为：

$C\left(T\right)=\{\begin{array}{l}5.0261{\text{e}}^{-15.8903T}+\frac{T}{0.3927T+0.1176}\left(T\le 0.165\right)\\ 1.273338\left(T>0.165\right)\end{array}$ (3)

4) 定位尺寸特征的成本–公差数学函数为：

$C\left(T\right)=\{\begin{array}{l}8.2369{\text{e}}^{-35.8049T}+1.307{\text{e}}^{\frac{0.0063}{T}}\left(T\le 0.13\right)\\ 1.23036\left(T>0.13\right)\end{array}$ (4)

5) 轴(孔)位置度尺寸特征的成本–公差数学函数为：

$C\left(T\right)=2.784{\text{e}}^{-36.61T}+1.125{\text{e}}^{\frac{0.0075}{T}}$ (5)

6) 轴对轴的跳动(同轴度)尺寸特征的成本–公差数学函数为：

$C\left(T\right)=0.0373{\text{e}}^{-3.08T}$ (6)

在电机的装配尺寸链中，包含的加工特征有内孔尺寸特征、外圆尺寸特征、圆跳动和位置度等，不同的加工特征对应不同的加工成本–公差函数。根据电机装配尺寸链中各种不同组成环的加工特征，选择相应的加工成本–公差数学模型，电机径向装配各零件加工特征的加工成本模型为：

$C\left(t\right)={\displaystyle \underset{i=1}{\overset{n}{\sum }}C\left(t_i\right)}$ (7)

式中， $t_i$ 为零件公差， $C\left(t\right)$ 为产品总加工成本， $n$ 为公差个数。

2.2. 质量损失成本模型

质量成本是指企业为了保证产品达到满意的质量水平而发生的费用以及因为没有达到满意的质量水平而造成的损失成本 [9] 。为了能够度量产品因偏离特定质量特性目标值而造成的损失，田口博士提出了质量损失函数的概念。

假设产品的质量特征设为 $y$ ，目标值设为 $m$ ，当质量特征 $y$ 等于目标值 $m$ 时，质量损失最少，此时的损失为零。用函数 $L\left(y\right)$ 来表示与质量特征值 $y$ 所对应的损失，质量损失函数为：

$L\left(y\right)=k{\left(y-m\right)}^2$ (8)

式中， $k$ 为与 $y$ 无关的质量损失系数。

通常，零件几何尺寸与设计值的偏差是双向对称的，则在极限偏差状态时，可得：

$y-m=\frac{T}{2}$ (9)

产品装配后的质量特性主要是通过封闭环的公差属性来反映，由产品的公差合格范围要求可知，当封闭环公差 $T>T_0$ 时，产品不合格。假设当产品不合格时所造成的质量损失为 $A$ ，则质量损失系数 $k$ 为

$k=\frac{4A}{T_0^2}$ (10)

因此，电机系统的质量损失成本模型为：

$L\left(t_i\right)={\displaystyle \underset{i=1}{\overset{n}{\sum }}\frac{A}{T_0{}^2}{t}_i{}^2}$ (11)

其中， $t_i$ -组成环 $i$ 的公差， $n$ 为组成环的数量。

根据电机的功能要求可知，气隙允许的变化范围为±0.2 mm，即允许的公差值为T₀ = 0.4 mm，结合电机生产厂家的相关统计数据，当电机气隙变化大于0.4 mm时，电机的质量损失成本为55元，即A = 55元，通过计算可以得到电机装配的质量损失系数k为1375，得到电机系统的质量损失成本模型L为：

$L\left(t_i\right)=343.75{\displaystyle \underset{i=1}{\overset{n}{\sum }}{t}_i{}^2}$ (12)

2.3. 约束条件

1) 装配尺寸链的功能要求约束

电机装配公差约束要求公差必须处于规定的公差范围内，进而保证装配质量，提升装配精度。概率法装配尺寸链功能约束公式为：

$t_0\ge \sqrt{{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\xi }_i{}^2{t}_i{}^2}}$ (13)

式中， $t_0$ 为封闭环的公差， ${\xi }_i$ 为相对分布系数， $n$ 为组成环个数。

2) 经济加工能力约束

在实际生产制造中，对于电机装配公差有着加工精度的约束，该约束要求每个工序加工的零件不超过实际生产中该零件所能实现的较为经济的加工工艺精度范围，约束公式为：

$t_{i\min }\le t_i\le t_{i\max }$ (14)

式中， $t_{i\min }$ 为第i个组成环的最小的加工能力公差， $t_{i\max }$ 为第i个组成环的最大的加工能力公差。

综上可得，多目标多优化的电机产品装配公差优化数学模型如下：

$\begin{array}{l}\{\begin{array}{l}\min F\left(x\right)=\left[C\left(t\right),L\left(t\right)\right]\\ C\left(t\right)={\displaystyle \underset{i=1}{\overset{n}{\sum }}C\left(t_i\right)}\\ L\left(t\right)=\frac{A}{T_0^2}{\displaystyle \underset{i=1}{\overset{n}{\sum }}{t}_i{}^2}\end{array}\\ s.t\{\begin{array}{l}\sqrt{{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\xi }_i{}^2{t}_i{}^2}}\le t_0\\ t_{i\min }\le t_i\le t_{i\max }\end{array}\end{array}$ (15)

3. 多目标粒子群算法

3.1. 基本原理

多目标粒子群算法继承了传统粒子群优化算法快速收敛、参数易调节的优点，同时改善了多目标进化算法收敛速度慢、易陷入局部最优解的不足 [10] 。

粒子群中每个粒子被看作一个潜在的最优解，设粒子群的搜索空间为D维，种群规模为 $N$ ，第 $i$ 个粒子的位置为 $x_i=\left(x_{i1},x_{x2},\cdot \cdot \cdot ,x_{iD}\right)$ ，速度为 $v_i=\left(v_{i1},v_{x2},\cdot \cdot \cdot ,v_{iD}\right)$ ，该粒子所经历的历史最优位置为 $p_i=\left(p_{i1},p_{x2},\cdot \cdot \cdot ,p_{iD}\right)$ ，即个体最优pbest，整个种群所有粒子经历过的最好的位置记为 $p_g=\left(p_{g1},p_{g2},\cdot \cdot \cdot ,p_{gD}\right)$ ，即全局最优gbest。粒子群算法采用下列公式更新粒子的速度与位置：

$v_{id}^{k+1}=\omega v_{id}^k+c_1{r}_1\left(p_{id}^k-x_{id}^k\right)+c_2{r}_2\left(p_{gd}^k-x_{id}^k\right)$ (16)

$x_{id}^{k+1}=x_{id}^k+v_{id}^{k+1}$ (17)

式中， $i=1,2,\cdot \cdot \cdot ,N$ ， $d=1,2,\cdot \cdot \cdot ,D$ ； $\omega$ 为惯性权重，通常取0到1之间的小数， $k$ 为当前迭代次数； $c_1$ ， $c_2$ 为学习因子， $r_1$ 和 $r_2$ 为[0, 1]之间的随机数。

粒子群优化算法的速度更新主要包括三部分：第一部分为粒子自身速度影响，表示上次粒子速度大小和方向；第二部分为自我记忆影响，是从当前点指向粒子自身最好点的一个矢量，表示粒子的动作来源于自己经验的部分；第三部分为受群体影响，是一个从当前点指向种群最好点的矢量，表示粒子间的信息共享与合作。粒子就是通过自己的经验和同伴中最好的经验来决定下一步的运动，粒子的速度是三个方向速度的加权矢量和。粒子位置更新示意图如图1所示。

Figure 1. Schematic diagram of particle position update

图1. 粒子位置更新示意图

3.2. 参数设置

在迭代计算过程中，使惯性权重 $\omega$ 呈线性递减，使其在前期有较好的全局搜索能力，能够快速靠近全局最优区域，在后期有较好的局部搜索能力，能够准确搜索到全局最优解 [11] 。线性递减惯性权重公式如下：

$\omega ={\omega }_{\max }-\frac{{\omega }_{\max }-{\omega }_{\min }}{T_{\max }}\times t$ (18)

式中， ${\omega }_{\max }$ 、 ${\omega }_{\min }$ 分别表示惯性权重最大值和最小值，一般情况下两者取值分别为0.9和0.4； $T_{\max }$ 和 $t$ 分别表示最大迭代次数和当前迭代次数。

在进化过程中对所有非支配解按拥挤距离降序排列，从排名靠前的部分粒子中随机选择一个作为全局最优解。拥挤距离的数学表达式为：

$d_i={\displaystyle \underset{j=1}{\overset{n}{\sum }}\frac{f_{j,i+1}-f_{j,i-1}}{f_{j,\max }-f_{j,\min }}}$ (19)

其中， $d_i$ 表示粒子 $i$ 间的拥挤距离， $j=1,2,\cdot \cdot \cdot ,n$ 表示目标的数量， $f_{j,i+1}$ 与 $f_{j,i-1}$ 分别表示与粒子 $i$ 临近的两个粒子在目标 $j$ 方向的数值， $f_{j,\max }$ 与 $f_{j,\min }$ 分别表示粒子在目标 $j$ 方向上的最大值和最小值。

在粒子群外部建立一个精英解集，以保存每一次更新的全局最优粒子，因此精英解集是粒子群算法种群中处于支配地位的个体的集合。当解集中粒子数量大于指定数量时，利用拥挤距离法对粒子进行排序和筛选，精英策略具体执行步骤为：

1) 初始化后根据支配关系得到精英解集；

2) 位置更新后的种群与精英解集合并；

3) 根据支配关系更新精英解集，并按照拥挤距离排序删除大于种群数的粒子，保留拥挤距离大的粒子。

采用拥挤距离来选择全局最优解，此方法无需用户定义其他参数以保证种群的多样性，从而赋予了算法更好的计算复杂度。在精英解集中，选取拥挤距离为前10%的粒子构成全局最优解集池。在速度迭代过程中，每次从全局最优解集中随机选取一个粒子作为全局最优解，将粒子的历史最优位置与粒子的当前位置进行比较来选择个体最优解。

3.3. 实现步骤

多目标粒子群算法流程如图2所示，具体实现步骤如下：

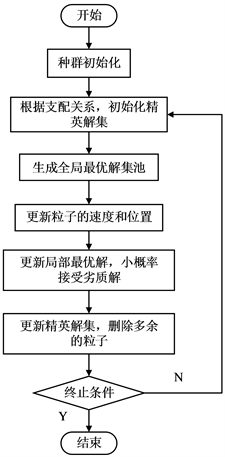
Figure 2. Flow chart of multi-objective particle swarm optimization algorithm

图2. 多目标粒子群优化算法流程图

1) 设定粒子群参数，并初始化种群；

2) 根据初始种群的支配关系得到初始种群的精英解集；

3) 开始迭代，计算每个粒子的拥挤距离并生成全局最优解集池；

4) 随机选择全局最优解，执行粒子群算法的速度更新公式和位置更新公式，并计算新粒子目标；

5) 更新局部最优解，并设定小概率接受劣质解；

6) 合并新种群以及精英解集，根据支配关系更新精英解集，并根据拥挤距离删除大于种群数的粒子；

7) 迭代结束后，导出精英解集。

4. 电机系统的公差优化

图3为电机模型的内部装配图，图中FR为电机的装配功能要求，该装配体由八部分组成：定子、机壳、前端盖、后端盖、左轴承、右轴承、转轴、转子。

Figure 3. Motor assembly

图3. 电机装配体

电机各组成环初始公差和允许变动范围如表1所示。

Table 1. Initial tolerance and variation range of each component ring

表1. 各组成环的初始公差和变动范围

利用多目标粒子群算法对所建立的电机多目标多约束模型进行优化求解，设置初始粒子数目为200，学习因子 $c_1=c_2=1.5$ ，惯性权重最小值为0.4，最大值为0.9，经过100次迭代后，计算时长为12.099 s，得到精英解集。结合得到的解集，综合考虑质量损失成本和加工成本，确定各组成环公差的优化值。优化后的公差值应符合国家标准，因此应当需要参照国家标准对优化后的公差值进行修订，公差优化值和修订值如表2所示。

Table 2. Tolerance optimization result

表2. 公差优化结果

5. 优化结果分析

为了验证文中的公差优化方法的有效性，本节将对电机优化前后的装配成功率和优化前后的成本进行对比分析。

1) 优化前后装配成功率分析

根据各组成环初始公差值和利用算法优化得到的公差优化值，运用3 DCS仿真软件对装配成功率进行模拟仿真，3 DCS是一款完全集成于CATIA V5三维的装配三维尺寸链仿真分析软件，其公差分析原理是基于蒙特卡洛模拟法，通过大量的装配仿真模拟，将各零件的偏差进行累积分析，以得到封闭环的分布规律。本文所引用的电机气隙变化范围为±0.2 mm，即允许公差值为0.4 mm，电机气隙公称尺寸为0. 75 mm。

在3 DCS软件中采用基于特征“Feature Move”方式对电机各零部件进行装配定位，公差定义均采用基于特征“Feature Tolerance”方式进行定义 [12] ，公差分布设置为正态分布，通过基于特征“Feature Measure”方式定义测量目标，分别选择转子外表面和定子内表面作为特征面，在间隙要求中设置公差值合格范围为0.4 mm，共选择5000个样本进行仿真模拟，优化前后的电机装配气隙分布图如图4和图5所示。

图4和图5中横轴表示电机气隙的变动范围，绿色部分为满足装配要求的概率，红色部分表示超出装配要求的概率。由图4和图5可知，经过算法优化后装配成功率比优化前的装配成功率高11.92%。

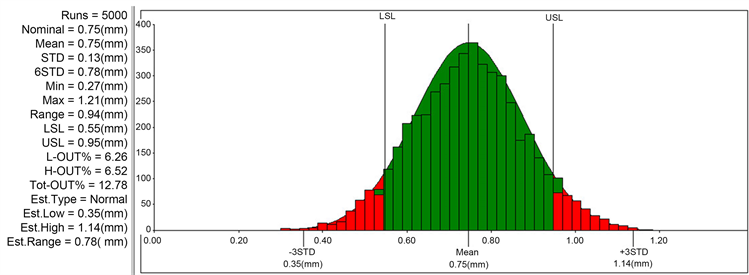
Figure 4. Air gap distribution of motor assembly before optimization

图4. 优化前的电机装配气隙分布图

Figure 5. Air gap distribution of motor assembly after optimization

图5. 优化后的电机装配气隙分布图

2) 优化前后成本分析

根据初始公差值和优化后的公差值，分别代入到目标函数中，计算得到优化前后电机模型的成本，结果如表3所示。

Table 3. Cost comparison before and after optimization

表3. 优化前后成本对比

由表3可以看出，在约束条件下，各优化目标函数的成本均降低，公差优化后电机加工成本减少7.3523元，电机质量损失成本减少1.0312元，优化后的电机总成本减少了8.3835元，经过算法优化后，相较于初始成本，电机的加工成本、质量损失成本和总成本分别下降35.29%、7.54%、24.29%。由此表明本文公差优化结果在保证产品的装配质量，提高装配成功率的同时，还能降低成本。

6. 结论

本文构建了以加工成本和质量损失成本为目标函数，以满足装配尺寸链的功能要求和经济加工能力为约束条件的电机多目标多约束公差优化模型，并采用多目标粒子群优化算法对目标模型进行求解，运用3 DCS仿真分析，结果显示优化分配后的公差降低了超差率，装配成功率较优化前提高了11.92%，同时使得总成本下降了约24.29%，为电机的公差分析及性能改进提供设计依据和参考。