1. 研究背景及意义
多维时间序列是指在一段时间内按照一定的时间间隔频率对同一目标的多个变量值进行采样的一段数据,其具有数据量大、数据维度高和特征复杂等特点。近十几年来,随着物联网(IOT)及大数据技术的蓬勃发展,带来了数据的爆发式增长,其中多维时间序列更是随着硬件设备的快速迭代迎来了其增长的黄金时期。现在,多维时间序列已经普遍存在于各行各业,包括交通运输业、航空航天产业、医疗产业、金融产业、现代工业等。
然而,在多维时间序列的收集、存储过程中,由于种种影响因素,会使得存储的数据部分缺失 [1],进而造成对下游数据应用的困扰。例如在采集天气情况数据时,由于传感器或设备自身的故障原因,导致采集的温度、空气湿度、风速等指标数据部分缺失,造成在后续的天气状况预测任务中出现偏颇;在现代智能医疗设备收集患者身体健康状况数据时,由于设备连接不正确、节约成本等因素,造成记录患者身体状况的各项指标数据缺失,使得医生在诊断患者身体状况时出现偏差。针对于此,本文将生成式对抗网络引入多维时间序列缺失值的补插任务中,并利用自编码器替换生成式对抗网络中的生成器。此外,在自编码器中引入注意力机制,使得补全后的数据符合原始数据的特征分布,进一步提高数据的可用性。无论对于后续基于该数据的预测任务还是数据建模等,都起到了关键性支持作用,这使得对于多维时间序列的整体数据挖掘任务更加完善。
2. 多维时间序列缺失值补插算法现状
2.1. 基于删除的补插方法
基于删除的多维时间序列补插方法主要是通过对原始数据中的缺失值进行删除操作,使得原始多维时间序列中不再包含缺失值,进而可以将其应用于下一步的数据建模及下游应用。在原始多维时间序列缺失率不高或者原始缺失数据所代表的含义不重要的情况下,这是一种常用的策略。然而,目前所收集的大部分多维时间序列都具有数据量大、数据含义深等特点,用上述方法进行操作时不但会进一步损害数据本身的完整性,还会使得在进行下游数据应用时由于没有某一维度的信息进而出现分析偏差。
2.2. 基于统计的补插方法
基于统计的修复方法依赖于统计模型来修复缺失值,该类方法具有计算复杂度低,易操作等特点。其中,就近填充包括前推法(LOCF)与后推法(NOCB) [2],主要通过利用缺失值位置的前一个观测值或者后一个观测值对当前缺失值位置进行一个填充操作。特征值填充法 [3] 主要通过对整体数据进行简单统计,计算其均值、中值、中位数等特征值对其中的缺失值进行修复操作。该方法计算简单,但是没有考虑到数据中的时序性关系且降低了整体数据的方差。逐步回归 [4] (Stepwise Regression)可以用来处理具有多个变量的时间序列,从大量可选择的变量中逐步选取重要的变量进行分析。其做法是观察统计值,例如利用R-square、t-stats、AIC等指标来辨别重要的变量并对其进行分析,从而实现对缺失值的预测。
2.3. 基于机器学习的补插方法
以往的许多实验已经证明,基于机器学习的多维时间序列的缺失值补插方法是有效地。其中,基于自回归模型(Auto-Regress)的修复算法主要包括ARMA [5] 模型、ARIMA [6] 模型。对于ARMA模型来说,自回归模型(AR)主要通过探索当前缺失值与历史真实值之间的关系,利用历史数据对当前缺失值位置的数据进行预测填补。此外,移动平均模型(MA)主要关注的是自回归模型中的误差项的累加,移动平均模型能够有效的消除预测中的随机波动,进而减小ARMA模型的误差。对于ARIMA模型来说,需要先对非平稳的多维时间序列进行差分运算,在获得平稳的数据集后计算其自相关系数(ACF)和偏自相关系数(PACF),最终通过分析得到最佳的阶层和阶数,进而通过对模型不断校验最终获取合适的修复值。基于矩阵分解 [7] (Matrix Factorization)的方法不但在推荐系统上有所建树,在多维时间序列缺失值的修复任务中也被证明有效。其主要思想为通过对原始数据矩阵进行分解、重构,以查找数据之间的相关性并完成缺失值的修复,这是一种经典的协同过滤方法。
2.4. 基于深度学习的补插方法
近年来,随着深度学习在各领域的广泛应用,其在多维时间序列的补插任务中也展现了其强大的计算能力。其中,RNN模型在时间序列的补插任务中应用尤其广泛。GRU-D [8] 将GRU网络引入到时间序列中缺失值的建模中,并对GRU网络进行修改,利用时间序列的时间间隔捕获观测值与缺失值之间的关系。BRITS [9] 提出一种新的基于双向循环神经网络(Bidirectional Recurrent Neural Network)的时间序列缺失值修复方法,该方法将缺失值看作双向RNN的变量,在对该变量进行计算时不但利用的正向传播的信息,还利用了反向梯度传播的相关信息。在这种情况下,缺失值的修复在一致性约束下得到正向和反向的延迟梯度,从而使得估算的缺失值更加准确。E2GAN [10] 模型在GAN的生成器前面引入了编码器结构,从而使得模型的输入不在是从潜在空间中探寻隐向量,而是直接对带有缺失值的多维时间序列进行降维处理,然后生成器对降维后的数据进行特征学习。通过这一变化减少了模型在潜在空间中的训练过程,从而使得整个网络的训练时间减少。
3. 改进的生成式对抗网络模型结构
3.1. 生成式对抗网络
生成式对抗网络的理念是基于零和博弈的思想,由生成器和判别器组成,其网络结构图如图1所示,其中红色叉号代表缺失数据。该图的生成器由自编码器网络组成,判别器由GRU网络组成。生成器(G)接受一个随机“噪声”z作为输入,通过神经网络的不断学习生成一个新的样本G(z)。生成器的目的是利用判别器的负反馈机制,使得生成足够真实到新样本以达到判别器的识别要求。判别器(D)接受真实的样本数据和生成的样本数据G(z)作为输入,并对输入数据执行分类任务,即区分数据是生成的还是真实的。判别器的目的是对越来越真实的G(z)进行判别,直到二者最终达到稳定的状态。其算法原理如公式(1)所示:
(1)
其中,D(x)代表判别器能够识别输入的数据是生成器生成的概率,G(z)代表随机噪声经过生成器网络后经过高维映射形成的假样本数据,Pdata(x)代表原始数据的特征分布,P(z)代表生成器生成的样本数据的特征分布。
对于本文的生成对抗网络的生成器来说,其输入是带有缺失值的多维时间序列,而不是从潜在空间中采样一个随机“噪声”z,输出的是一个完整的高维样本G(E(x)),原理变化如公式(2)所示:
(2)
其中,E(x)表示编码器处理的多元时间序列。通过上述方法不仅减少了神经网络的训练时间,而且还将原始数据映射为低维向量,消除了潜在空间的随机采样,减少了训练过程中模型的随机性。
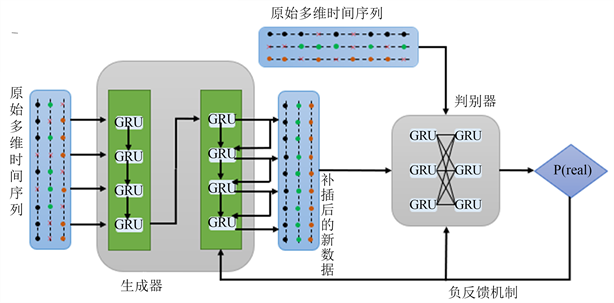
Figure 1. Initially improved generative adversarial network
图1. 初步改进的生成式对抗网络
3.2. 自编码器网络
自编码器 [11] 是一种应用于序列到序列的模型,它包含编码器和解码器结构,已被用于机器翻译、数据处理、图像填充等。编码器将输入序列转换为固定长度的向量;解码器将先前生成的定长向量转换为输出序列。这个工作流程与多维时间序列缺失值补插任务一致,可以将带有缺失值的数据转换为完整的数据。
如上所述,为了解决潜在空间随机采样“噪声”向量不稳定的问题,引入了以门控循环单元(GRU)为神经网络的自编码器模型。这样既解决了优化“噪声”向量导致训练时间过长的问题,又考虑了多维时间序列中时间间隔的问题。该方法将带有缺失值的多维时间序列输入到编码器中,进行特征提取和降维等一系列处理。之后,一个固定长度的潜在向量产生,然后,通过解码器对定长向量进行处理,并映射为完整的多维时间序列。
3.3. 注意力机制
注意机制 [12] 是目前神经网络中必不可少的模型,已被应用到机器翻译、语音识别等多个应用领域。这得益于它能够捕获能距离依赖特性,由于GRU [13] 模型是按顺序计算以实现远程依赖特征,将相隔较远的计算信息链接在一起需要多个时间步。对于GRU模型来说,距离越远,有效捕获特征信息的可能性越小。相反,注意机制可以通过权重计算将时间序列中相关的计算结果直接关联起来。因此,注意力机制可以有效地解决长距离依赖问题。
此外,不带有注意机制的自编码器模型主要利用生成器对输入序列进行编码,并将数据的所有信息转化为一个潜在向量,然后解码器利用这个潜在向量生成一个完整的新序列。这种将数据的所有信息转化为一个潜在向量的方法会导致信息丢失。其原因是固定长度的潜在向量所能包含的信息量有限,这导致解码器在解码时准确性下降。
因此,我们在自编码器模型中加入了注意力机制,即使用注意机制为输入的时间序列生成多个潜在向量,然后解码器利用这些潜在向量生成不同的缺失值,加入注意力机制后的对比图如图2所示。具体来说,对于不同缺失值的补插,所需要的信息是不同的,注意力机制使不同的潜在向量能够存储不同的信息,使解码器在计算不同的缺失值时能够利用不同的潜在向量。这有助于捕获和存储足够的原始时间序列的信息,从而有效地支持缺失值的补插。
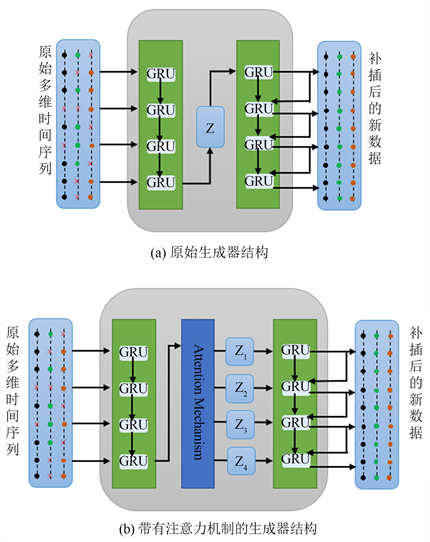
Figure 2. Effectiveness of attentional mechanism
图2. 注意力机制的效果
4. 实验结果与分析
4.1. 数据集及实验介绍
我们使用国际开源医疗数据集,即PhysioNet数据集来评估我们提出方法的性能。该数据集是一个公共的多维时间序列数据集,其中包括来自重症监护病房的4000份记录。每一份记录都包含患者进入病房的前48小时内的身体状况数据,共记录了患者的41项病情指标。在这4000名患者中,共有554人在医院死亡,作为阳性标记,因此我们通过对患者死亡率的预测来验证我们提出的模型的补插准确率。
此外,由于数据集中的缺失值已经无法再次获取,所以我们随机删除一定比例的原始数据,然后用我们的方法对原始数据中删除的值进行补插操作,最后通过计算被删除数据与被补插数据的均方误差(MSE)来验证我们提出模型的准确性。在本文中,我们从Physionet数据集中随机选择20%作为测试数据集,其他80%作为训练数据集。
4.2. 死亡率预测实验分析
将提出的模型(A-AEGAN,其中A代表注意力机制,AE代表自编码器,GAN代表生成式对抗网络)与E2GAN和GRU-D进行比较并做对比实验。我们分别对这两种模型进行了五次实验,即用这两种模型对缺失的多维时间序列进行补插操作,最终得到完整的多维时间序列。为了保证实验的准确性,我们将补插后多维时间序列喂给相同RNN分类模型并进行死亡率的预测。RNN分类模型的死亡率预测结果如表1所示。

Table 1. Accuracy of mortality prediction
表1. 死亡率预测准确性
从表中可以看出,在五次实验中,基于E2GAN模型和GRU-D模型补插的数据在死亡率预测任务中的准确率均低于A-AEGAN模型。五次平均预测精度以A-AEGAN模型的0.8703分取得了最高的成绩。A-AEGAN模型的预测精度比E2GAN模型提高6.1%左右,比GRU-D模型的准确率提高10.1%左右。值得注意的是,基于A-AEGAN模型推算数据的死亡预测准确率最高可达0.8906。这说明我们提出的模型在多维时间序列缺失值的补插任务中优于现有最优模型。
4.3. 死亡率预测AUC分数实验分析
AUC是ROC (Receiver Operating Characteristic Curve)曲线下面积 [14],是专门用于分类任务的一个指标,能够在样本标签分布不均匀的情况下也能很好的评判模型分类结果的优劣。在本文中,采用AUC指标评判模型在分类任务中的优劣,能够更加全面的反应模型修复的准确性。
PhysioNet数据集中的验证标签为554个,为了防止在测试集上进行实验验证时出现样本标签分布不均匀的情况,本文引入AUC指标来进一步评判模型修复的准确率。同样的,仍然进行5轮实验,然后利用修复后的数据进行死亡预测,最终的预测准确率如表2所示。
从表中可以看到,本文提出的模型比E2GAN模型和GRU-D模型获得了更高的AUC分数。其中,基于A-AEGAN模型修复数据的分类模型取得了最先进的结果,其平均AUC得分为0.8027,比E2GAN模型的平均AUC分数提高了5.1%。值得注意的是,A-AEGAN模型在第一轮实验中获得了最高的AUC得分0.7593。这进一步说明了本文提出的模型在多维时间序列缺失值修复任务中的优越性。

Table 2. Mortality prediction AUC scores
表2. 死亡率预测AUC分数
4.4. 基于回归任务的MSE评估
均方误差(MSE) [15] 是反映估计值和实际值之间差异程度(越小越好)的变量。在本实验中,使用MSE来评估原始多维时间序列与补插的多维时间序列之间的差异。如前所述,由于原始时间序列中存在缺失值,我们无法直接计算出原始时间序列与推算的时间序列之间的MSE。因此,我们删除一定比例的数据,然后计算推算数据与删除数据之间的MSE。基于生成式对抗网络模型在不同缺失率情况下的实验结果如图3所示。

Figure 3. Comparison of MSE with different missing rates
图3. 不同缺失率下MSE的比较
从图中我们可以看到在不同缺失率情况下,我们的模型都是优于E2GAN模型的,这进一步表明了我们提出模型的优越性。随着缺失率的增加,模型计算出的MSE逐渐增大,这表明原始数据的可用性逐渐变差。此外,在缺失率为70%的时候,两个模型计算出的MSE差距变小,这表明数据在变得极其不可用的情况下,对于缺失值的补插会变得极其困难。
5. 总结
本文利用多维时间序列的特性,提出了一种多维时间序列缺失值修复算法模型。首先本文选取生成式对抗网络作为基础框架,该网络主要由生成器结构和判别器结构组成,二者通过相互博弈实现生成数据的目的,本文便是利用该网络强大的生成能力实现对缺失数据的修复。其次,将自编码器模型引入生成式对抗网络,实现对其改进,利用自编码器来替换生成器结构,这样不但提高了生成式对抗网络对原始多维时间序列的特征捕获能力,而且还减少了原始生成式对抗网络需要从潜在空间中探寻噪声向量并进行优化的不稳定性。最后,在自编码器中分别引入注意力机制,构建注意力分数矩阵,使得自编码器在进行缺失值生成时不但能够利用缺失值所在维度的数据,还能够利用其他维度的关联性信息,进一步提高了模型修复的准确率。