变系数分数阶偏微分方程的数值解法

Numerical Solution of Fractional Partial Differential Equations with Variable Coefficients

摘要: 本文旨在对二维具有变系数的分数阶偏微分方程构造一种有效的有限差分格式，通过对误差的分析得到该差分格式的收敛阶为 ，其中τ表示时间步长，h₁,h₂表示空间步长，1<α<2。通过能量分析方法证明所提出的有限差分格式的收敛性和稳定性，最后，我们利用高斯迭代法求解给出的数值算例，通过对误差的处理得到上述格式的收敛阶，并通过图像进一步说明该差分格式的有效性，即通过有限差分格式得到的数值解既能保持原问题表现出来的性质，又可以在一定误差允许的范围内满足工程问题的需要。

Abstract: The purpose of this paper is to construct an efficient finite difference scheme for two-dimensional fractional partial differential equations with variable coefficients. By analyzing the error, the con-vergence order of the difference scheme is , where τ denotes time step, h₁,h₂ denote space step, 1<α<2 . The convergence and stability of the proposed finite difference scheme are proved by energy method. Finally, we use Gauss iterative method to solve the given numerical example, the convergence order of the above scheme is obtained by dealing with the er-ror, and the effectiveness of the scheme is further illustrated by the image, that is, the numerical solution obtained by the finite difference scheme can not only keep the properties of the original problem, but also meet the needs of engineering problems within a certain error allowable range.

1. 引言

近几十年来，随着大家对反常运输现象和反常扩散过程的兴趣越来越大 [1] [2] ，与整数阶偏微分方程相比，分数阶偏微分方程由于其自身具有非局域性、可记忆性和遗传性，所以更容易模拟记忆相关现象和复杂介质。此外，还发现分数阶偏微分方程可以更好地适用于物理、生物科学、工程、金融等各个领域的数学模型，如现实生活中物质的电学性质，包括电磁和电化学、流体力学、粘弹性理论 [3] 、图像去噪 [4] 、金融期权定价的Black-Scholes模型 [5] 等。虽然一些特殊形式的分数阶偏微分方程的解析解可以用相应的方法求解，如积分变换的拉普拉斯变换 [6] ，但大多数分数阶偏微分方程很难找到它们的解析解。

然而，在工程中，可控误差可以允许在一定范围内，这促使我们寻找有效的数值方法来求解分数阶偏微分方程。到目前为止，已经提出了许多求解分数阶偏微分方程的数值方法，如有限差分法 [7] [8] 、有限元法、谱方法、矩阵法和小波方法等。近几年来，有限差分方法在各种模型中的应用越来越广泛，其中Ji等人 [9] [10] 通过有限差分方法求解时间分数阶Dual-Phase-Lagging热传导模型。据作者所知，许多处理分数阶偏微分方程的有限差分方法大致可分为两类，一种是将其转换为积分形式，以便进一步研究分数阶积分算子，另一种是对时间分数阶导数的直接近似，包括基于生成函数的Grunwald-Letnikov公式和用于本文模型的L1公式。其他数值方法详见参考文献 [11] [12] [13] [14] 。

而本文研究的数学模型也可以称作分数阶对流–扩散波方程，是用时间分数阶Caputo导数代替了对流扩散方程中的时间一阶导数演变而来，描述了流体的传质、传热等过程，即当 $\Omega$ 为求解区域，而 $\partial \Omega$ 为 $\Omega$ 的边界区域时，

$\begin{array}{l}\frac{{\partial }^{\alpha }u}{\partial t^{\alpha }}-\frac{\partial }{\partial x}\left(p_1\left(x,y\right)\frac{\partial u}{\partial x}\right)-\frac{\partial }{\partial y}\left(p_2\left(x,y\right)\frac{\partial u}{\partial y}\right)+r_1\left(x,y\right)\frac{\partial u}{\partial x}+r_2\left(x,y\right)\frac{\partial u}{\partial y}+q\left(x,y\right)u\\ =f\left(x,y,t\right),x\in \Omega \backslash \partial \Omega ,t\in \left(0,T\right],\end{array}$ (1)

初始条件

$u\left(x,y,0\right)=\varphi \left(x,y\right),\frac{\partial u\left(x,y,0\right)}{\partial t}=\psi \left(x,y\right),\left(x,y\right)\in \Omega ,$ (2)

边界条件

$u\left(x,y,t\right)=\phi \left(x,y,t\right),\left(x,y\right)\in \partial \Omega \times \left(0,T\right],$ (3)

其中 $1<\alpha <2$ ，并且 $\frac{{\partial }^{\alpha }u}{\partial t^{\alpha }}$ 定义为Caputo分数阶导数，即

$\frac{{\partial }^{\alpha }u}{\partial t^{\alpha }}=\frac{1}{\Gamma \left(2-\alpha \right)}{\displaystyle {\int }_0^t\frac{{\partial }^{2}u\left(x,s\right)}{\partial s^2}}\frac{\text{d}s}{{\left(t-s\right)}^{\alpha -1}}.$

由于变系数偏微分方程比常系数偏微分方程应用更广泛，研究变系数偏微分方程更有意义 [15] 。将原始方程转化为特殊的等价形式，提出了一类分数阶流动/不流动对流扩散方程的高阶数值方法，克服了变系数带来的困难。在 [16] 中，空间导数用四阶紧致有限差分法离散，时间导数用L1近似与Crank-Nicolson技术耦合离散，从而克服了变系数的困难。通过 [17] ，我们可以知道通过指数变换可以大大简化时滞问题，从而可以使用变系数四阶紧算子，基于紧算子和降阶方法，导出了数值格式，然后可以导出收敛性和稳定性 [18] 。用极坐标表示二维时间分数阶扩散波方程的有限差分格式，并用交替方向隐式方法求解，将二维问题分解为两个独立的一维问题。据作者所知，很少有研究该方程的文章，所以本文的工作是有意义的。在本文中，首先我们利用有限差分方法求解出复杂的二维变系数分数阶偏微分方程，通过迭代法进一步减少运算成本，也可以令变系数为常数，进而也可以得到求解常系数偏微分方程的数值方法，其次我们不仅从理论上证明了该有限差分格式的有效性，还在数值算例中进一步验证了理论结果。

在本文的第二节中，我们通过一致网格剖分对求解区域进行剖分，给出在下面的文章中使用的基本符号，然后基于有限差分法构造变系数对流–扩散波方程的差分格式，并估计了差分格式引起的截断误差。我们还在第三节中给出了所提出方案的收敛性和稳定性。最后，我们通过数值算例验证了该方法的收敛阶，并通过误差图像验证了该差分格式是有效的。

2. 差分格式的建立

首先将求解区域的空间方向分别划分为均匀一致网格，其中x方向的空间步长为 $h_1=\left(b-a\right)/m_1$ ， $x_i=a+i{h}_1$ ， $0\le i\le m_1$ ，y方向的空间步长为 $h_2=\left(d-c\right)/m_2$ ， $y_j=c+j{h}_2$ ， $0\le j\le m_2$ ，对时间方向进行均匀一致剖分，时间步长 $\tau =T/N$ ，时间节点 $t_n=n\tau$ ， $0\le n\le N$ 。

假设 $u=\left\{u_{i,j}^n|0\le i\le m_1,0\le j\le m_2,0\le n\le N\right\}$ 是在网格节点上的网格函数，定义下面的记号：

$u^{n-\frac{1}{2}}=\frac{1}{2}\left(u^n+u^{n-1}\right),{\delta }_t{u}^{n-\frac{1}{2}}=\frac{1}{\tau }\left(u^n-u^{n-1}\right),$

${\delta }_x{u}_{i-\frac{1}{2},j}=\frac{1}{h_1}\left(u_{i,j}-u_{i-1,j}\right),{\Delta }_x{u}_{i,j}=\frac{u_{i+1,j}-u_{i-1,j}}{2h_1},$

${\delta }_x^2{\left(p_{1}u\right)}_{i,j}=\frac{1}{h_1}\left({\left(p_1\right)}_{{}_{i+\frac{1}{2},j}}{\delta }_x{u}_{i+\frac{1}{2},j}-{\left(p_1\right)}_{{}_{i-\frac{1}{2},j}}{\delta }_x{u}_{i-\frac{1}{2},j}\right),$

${\delta }_{\tau }^{\alpha }\left({\delta }_t{u}^{n-\frac{1}{2}},\psi \right)=\frac{1}{\Gamma (2-\alpha )}\frac{1}{\tau }\left[a_0{\delta }_t{u}^{n-\frac{1}{2}}-{\displaystyle \underset{k=1}{\overset{n-1}{\sum }}\left(a_{n-k-1}-a_{n-k}\right){\delta }_t{u}^{k-\frac{1}{2}}}-a_{n-1}\psi \right],$

其中

$a_l={\displaystyle {\int }_{t_l}^{t_{l+1}}\frac{\text{d}t}{t^{\alpha -1}}}=\frac{{\tau }^{2-\alpha }}{2-\alpha }\left[{\left(l+1\right)}^{2-\alpha }-l^{2-\alpha }\right],l\ge 0.$

本文利用有限差分方法对本文的模型(1)~(3)建立差分格式，即对于时间分数阶导数，利用Sun等人 [19] 文章中的L1公式进行逼近，则局部截断误差为 ${\rm O}\left({\tau }^{3-\alpha }\right)$ ，对于空间变系数偏导数部分，令 $v_1=\partial u/\partial x$ ， $v_2=\partial u/\partial y$ ，而 ${\left(v_1\right)}_{i,j}^n=v_1\left(x_i,y_j,t_n\right)$ ， ${\left(v_2\right)}_{i,j}^n=v_2\left(x_i,y_j,t_n\right)$ ，即在点 $\left(x_i,y_j,t_n\right)$ 处利用Taylor展开式，利用二阶差商近似二阶偏导数，即

$\begin{array}{c}\frac{\partial }{\partial x}\left(p_1\frac{\partial u}{\partial x}\right)\left(x_i,y_j,t_n\right)=\frac{\partial v_1}{\partial x}\left(x_i,y_j,t_n\right)=\frac{{\left(v_1\right)}_{i+\frac{1}{2},j}^n-{\left(v_1\right)}_{i-\frac{1}{2},j}^n}{h_1}-\frac{h_1^2}{24}{v^{‴}}_1\left({\xi }_1,y_j,t_n\right)\\ =\frac{{\left(p_1\right)}_{i+\frac{1}{2},j}{\delta }_x{u}_{i+\frac{1}{2},j}^n-{\left(p_1\right)}_{i-\frac{1}{2},j}{\delta }_x{u}_{i-\frac{1}{2},j}^n}{h_1}+{\rm O}\left(h_1^2\right),\end{array}$ (4)

同理

$\begin{array}{c}\frac{\partial }{\partial y}\left(p_2\frac{\partial u}{\partial y}\right)\left(x_i,y_j,t_n\right)=\frac{\partial v_2}{\partial y}\left(x_i,y_j,t_n\right)=\frac{{\left(v_2\right)}_{i,j+\frac{1}{2}}^n-{\left(v_2\right)}_{i,j-\frac{1}{2}}^n}{h_2}-\frac{h_2^2}{24}{v^{‴}}_2\left(x_i,{\xi }_2,t_n\right)\\ =\frac{{\left(p_2\right)}_{i,j+\frac{1}{2}}{\delta }_x{u}_{i+\frac{1}{2},j}^n-{\left(p_2\right)}_{i,j-\frac{1}{2}}{\delta }_x{u}_{i-\frac{1}{2},j}^n}{h_2}+{\rm O}\left(h_2^2\right),\end{array}$ (5)

其中 ${\xi }_1\in \left(x_{i-\frac{1}{2}},x_{i+\frac{1}{2}}\right)$ ， ${\xi }_2\in \left(y_{j-\frac{1}{2}},y_{j+\frac{1}{2}}\right)$ 。

利用中心差分公式近似(1)式等号左边的第四项和第五项，可以得到

$\begin{array}{l}{r}_1\frac{\partial u}{\partial x}\left(x_i,y_j,t_n\right)={\left(r_1\right)}_{i,j}\frac{u_{i+1,j}^n-u_{i-1,j}^n}{2h_1}+{\rm O}\left(h_1^2\right),\\ r_2\frac{\partial u}{\partial y}\left(x_i,y_j,t_n\right)={\left(r_2\right)}_{i,j}\frac{u_{i,j+1}^n-u_{i,j-1}^n}{2h_2}+{\rm O}\left(h_2^2\right),\end{array}$ (6)

和时间离散保持一致，利用第n层和第n-1层的加权平均，结合(4)~(6)得到以下有限差分格式：

$\begin{array}{l}{\delta }_{\tau }^{\alpha }\left({\delta }_t{u}_{i,j}^{n-\frac{1}{2}},{\psi }_{i,j}\right)-{\delta }_x^2{\left(p_{1}u\right)}_{i,j}^{n-\frac{1}{2}}-{\delta }_y^2{\left(p_{2}u\right)}_{i,j}^{n-\frac{1}{2}}+{\left(r_1\right)}_{i,j}{\Delta }_x{u}_{i,j}^{n-\frac{1}{2}}+{\left(r_2\right)}_{i,j}{\Delta }_y{u}_{i,j}^{n-\frac{1}{2}}+q_{i,j}{u}_{i,j}^{n-\frac{1}{2}}\\ =f_{i,j}^{n-\frac{1}{2}},1\le i\le m_1-1,1\le j\le m_2-1,n\ge 1,\end{array}$ (7)

$u_{i,j}^0={\varphi }_{i,j},{\delta }_t{u}_{i,j}^0={\psi }_{i,j},0\le i\le m_1,0\le j\le m_2,$ (8)

$u_{0,j}^n=0,u_{m_1,j}^n=0,u_{i,0}^n=0,u_{i,m_2}^n=0,0\le i\le m_1,0\le j\le m_2,$ (9)

其中截断误差为 ${\rm O}\left({\tau }^{3-\alpha }+h_1^2+h_2^2\right)$ 。

3. 差分格式的收敛性稳定性分析

在证明以上差分格式的收敛性和稳定性之前，我们引入以下记号和引理：

$\Vert p_1{\delta }_x{u}^n\Vert =\sqrt{h_1{h}_2{\displaystyle \underset{j=1}{\overset{m_2-1}{\sum }}{\displaystyle \underset{i=1}{\overset{m_1}{\sum }}{\left(p_1\right)}_{i-\frac{1}{2},j}{\left({\delta }_x{u}_{i-\frac{1}{2},j}^n\right)}^2}}},$

$\Vert p_2{\delta }_y{u}^n\Vert =\sqrt{h_1{h}_2{\displaystyle \underset{j=1}{\overset{m_2}{\sum }}{\displaystyle \underset{i=1}{\overset{m_1-1}{\sum }}{\left(p_2\right)}_{i,j-\frac{1}{2}}{\left({\delta }_y{u}_{i,j-\frac{1}{2}}^n\right)}^2}}},$

${\left|p{u}^n\right|}_1=\sqrt{{\Vert p_1{\delta }_x{u}^n\Vert }^2+{\Vert p_2{\delta }_y{u}^n\Vert }^2},\Vert q{u}^n\Vert =\sqrt{h_1{h}_2{\displaystyle \underset{j=1}{\overset{m_2-1}{\sum }}{\displaystyle \underset{i=1}{\overset{m_1-1}{\sum }}{q}_{i,j}{\left(u_{i,j}^n\right)}^2}}}.$

引理1 [20] ：对任一 $G=G_1,G_2,\cdots$ 和q，我们有

${\displaystyle \underset{n=1}{\overset{N}{\sum }}\left[a_0{G}_n-{\displaystyle \underset{k=1}{\overset{n-1}{\sum }}\left(a_{n-k-1}-a_{n-k}\right)G_k-a_{n-1}q}\right]G_n}\ge \frac{t_N^{1-\alpha }}{2}\tau {\displaystyle \underset{n=1}{\overset{N}{\sum }}{G}_n^2}-\frac{t_N^{2-\alpha }}{2\left(2-\alpha \right)}{q}^2.$

引理2：当边界条件满足 ${\phi }_{i,j}^n=0$ ，即 ${\delta }_t{u}_{0,j}^{n-\frac{1}{2}}={\delta }_t{u}_{m_1,j}^{n-\frac{1}{2}}={\delta }_t{u}_{i,0}^{n-\frac{1}{2}}={\delta }_t{u}_{i,m_2}^{n-\frac{1}{2}}=0$ 时，有

$-h_1{h}_2{\displaystyle \underset{j=1}{\overset{m_2-1}{\sum }}{\displaystyle \underset{i=1}{\overset{m_1-1}{\sum }}{\delta }_x^2{\left(p_{1}u\right)}_{i,j}^{n-\frac{1}{2}}{\delta }_t{u}_{i,j}^{n-\frac{1}{2}}}}-h_1{h}_2{\displaystyle \underset{j=1}{\overset{m_2-1}{\sum }}{\displaystyle \underset{i=1}{\overset{m_1-1}{\sum }}{\delta }_y^2{\left(p_{2}u\right)}_{i,j}^{n-\frac{1}{2}}{\delta }_t{u}_{i,j}^{n-\frac{1}{2}}}}=\frac{1}{2\tau }\left({\left|p{u}^n\right|}_1^2-{\left|p{u}^{n-1}\right|}_1^2\right).$

证明：由 [20] 易得：

$\begin{array}{c}{h}_1{h}_2{\displaystyle \underset{j=1}{\overset{m_2-1}{\sum }}{\displaystyle \underset{i=1}{\overset{m_1-1}{\sum }}{\delta }_x^2{\left(p_{1}u\right)}_{i,j}^{n-\frac{1}{2}}{\delta }_t{u}_{i,j}^{n-\frac{1}{2}}}}=-\frac{h_1{h}_2}{2\tau }{\displaystyle \underset{j=1}{\overset{m_2-1}{\sum }}{\displaystyle \underset{i=1}{\overset{m_1}{\sum }}{\left(p_1\right)}_{i-\frac{1}{2},j}\left[{\left({\delta }_x{u}_{i-\frac{1}{2},j}^n\right)}^2-{\left({\delta }_x{u}_{i-\frac{1}{2},j}^{n-1}\right)}^2\right]}}\\ =-\frac{1}{2\tau }\left({\Vert p_1{\delta }_x{u}^n\Vert }^2-{\Vert p_1{\delta }_x{u}^n\Vert }^2\right),\end{array}$

$\begin{array}{c}{h}_1{h}_2{\displaystyle \underset{j=1}{\overset{m_2-1}{\sum }}{\displaystyle \underset{i=1}{\overset{m_1-1}{\sum }}{\delta }_y^2{\left(p_{2}u\right)}_{i,j}^{n-\frac{1}{2}}{\delta }_t{u}_{i,j}^{n-\frac{1}{2}}}}=-\frac{h_1{h}_2}{2\tau }{\displaystyle \underset{j=1}{\overset{m_2}{\sum }}{\displaystyle \underset{i=1}{\overset{m_1-1}{\sum }}{\left(p_2\right)}_{i,j-\frac{1}{2}}\left[{\left({\delta }_y{u}_{i,j-\frac{1}{2}}^n\right)}^2-{\left({\delta }_y{u}_{i,j-\frac{1}{2}}^{n-1}\right)}^2\right]}}\\ =-\frac{1}{2\tau }\left({\Vert p_2{\delta }_y{u}^n\Vert }^2-{\Vert p_2{\delta }_y{u}^n\Vert }^2\right),\end{array}$

以上两个式子相加即得证。

为了利用能量分析方法分析该差分格式的收敛性和稳定性，推得以下能量不等式：

引理3：若 $\left\{u_{i,j}^n\right\}$ 是差分格式的数值解，则存在常数 $C_1,C_2,C_3$ 使得序列

${\left|p{u}^N\right|}_1^2\le {\text{e}}^{8C_{1}T}\left(3{\left|p{u}^0\right|}_1^2+C_2\tau {\displaystyle \underset{n=1}{\overset{N}{\sum }}{\Vert f^{n-\frac{1}{2}}\Vert }^2}+C_3{\Vert \psi \Vert }^2+2{\Vert q{u}^0\Vert }^2+8C_1\tau k{M}_0\right),$ (10)

其中 $k\le N$ ， $N\tau \le T$ ， $M_0=\max \left\{{\left|p{u}^0\right|}_1^2,\cdots ,{\left|p{u}^{k-1}\right|}_1^2\right\}$ 。

证明：将差分格式(7)两边同时与 ${\delta }_t{u}_{i,j}^{n-\frac{1}{2}}$ 作内积，然后同时乘以 $\tau$ 并将n从1到N求和，结合引理1和引理2，利用Cauchy-Schwarz不等式和Gronwall不等式易得，具体证明见附录。

定理1 (稳定性)当 $\tau$ 足够小的时候，由差分格式(7)得出的数值解满足不等式(10)，则该差分格式是稳定的。

定理2 (收敛性)假设 $\left\{u\left(x,y,t\right)\right\}$ 是方程(1)~(3)的精确解， $\left\{u_{i,j}^n\right\}$ 是差分格式(7)~(9)的数值解，定义 $e_{i,j}^n=u\left(x_i,y_j,t_n\right)-u_{i,j}^n$ ，由差分格式的截断误差得存在常数c使得

$\left|e_{i,j}^n\right|\le c\left({\tau }^{3-\alpha }+h_1^2+h_2^2\right).$

4. 数值算例

在这一节中，本文通过两个算例来验证时间收敛阶和空间收敛阶，并且给出部分节点的精确解、数值解,最后通过误差图像分析该差分格式的意义。

例1：当 $p_1\left(x,y\right)=r_1\left(x,y\right)=p_2\left(x,y\right)=r_2\left(x,y\right)=q\left(x,y\right)=1$ 时，若方程(1)~(3)的精确解为

$u\left(x,y\right)=t^3\sin \left(x+y\right)$ ， $f\left(x,y\right)=\left(\frac{\Gamma \left(4\right)}{\Gamma \left(4-\alpha \right)}{t}^{3-\alpha }+3t^3\right)\sin \left(x+y\right)+2t^3\cos \left(x+y\right)$ ，其中 $\left(x,y,t\right)\in \left[0,1\right]\times \left[0,1\right]\times \left[0,1\right]$ ，为了减少收敛阶的计算量，通过 $h^2\approx {\tau }^{3-\alpha }$ 计算收敛阶，由表1可得，该差分格式的时间收敛阶是 ${\rm O}\left({\tau }^{3-\alpha }\right)$ ，空间收敛阶为 ${\rm O}\left(h_1^2+h_2^2\right)$ ，当 $U^N$ 为最后时刻的数值解， $u^N$ 是当 $t=t_N$ 时的精确解，则有

$\text{Error}={\Vert U^N-u^N\Vert }_{\infty },$

表2是当 $h_1=h_2=\frac{1}{50},\tau =\frac{1}{200},\alpha =1.5$ 时最后时刻的部分节点的数值解、精确解以及它们之间的误差，图1是最后时刻的误差图像，通过图像可以看出利用该差分格式逼近精确解是有效的，且误差可以控制在一定范围内。

Table 1. Error and convergence order of the numerical approximation in example 1

表1. 例题1中数值逼近的误差以及收敛阶

Table 2. Numerical solution, exact solution and the error at the last moment in example 1

表2. 例题1中最后时刻部分节点的数值解、精确解以及它们之间的误差

例2：当 $p_1\left(x,y\right)=r_1\left(x,y\right)=x$ ， $p_2\left(x,y\right)=r_2\left(x,y\right)=y$ ， $q\left(x,y\right)=x+y$ 时，若方程(1)~(3)的精确解为 $u\left(x,y\right)=t^3\sin \left(x+y\right)$ ， $\left(x,y,t\right)\in \left[0,1\right]\times \left[0,1\right]\times \left[0,1\right]$ ，其中

$f\left(x,y\right)=\left(\frac{\Gamma \left(4\right)}{\Gamma \left(4-\alpha \right)}{t}^{3-\alpha }+2\left(x+y\right)t^3\right)\sin \left(x+y\right)+\left(x+y-2\right)t^3\cos \left(x+y\right)$

由表3可得利用该差分格式解决变系数分数阶偏微分方程与常系数分数阶偏微分方程的时间收敛阶和空间收敛阶一致。表4是当 $h_1=h_2=\frac{1}{50},\tau =\frac{1}{200},\alpha =1.5$ 时最后时刻的部分节点的数值解、精确解以及

它们之间的误差，图2是最后时刻的误差图像。通过图像可以看出利用该差分格式逼近变系数方程的精确解仍然是有效的，且误差可以控制在一定范围内。

Figure 1. Error diagram at the last moment when $h_1=h_2=\frac{1}{50},\tau =\frac{1}{200},\alpha =1.5$ in example 1

图1. 例1中当 $h_1=h_2=\frac{1}{50},\tau =\frac{1}{200},\alpha =1.5$ 时最后时刻的误差图

Table 3. Error and convergence order of the numerical approximation in example 2

表3. 例题2中数值逼近的误差以及收敛阶

Table 4. Numerical solution, exact solution and the error at the last moment in example 2

表4. 例题2中最后时刻部分节点的数值解、精确解以及它们之间的误差

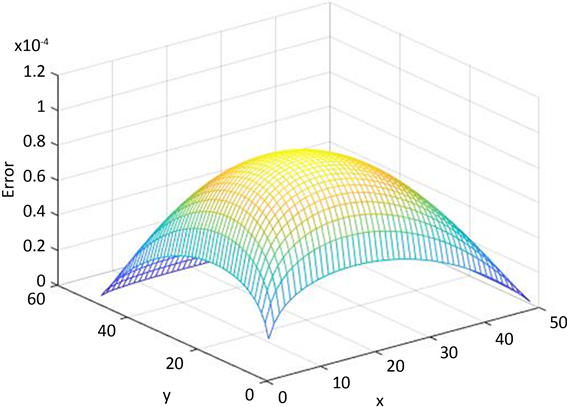
Figure 2. Error diagram at the last moment when $h_1=h_2=\frac{1}{50},\tau =\frac{1}{200},\alpha =1.5$ in example 2

图2. 例2中当 $h_1=h_2=\frac{1}{50},\tau =\frac{1}{200},\alpha =1.5$ 时最后时刻的误差图

5. 结论

本文不仅从理论上证明利用有限差分方法提出的有限差分格式对于求解二维变系数分数阶偏微分方程是收敛且稳定的，还从数值算例中得出了无论是常系数或者变系数问题，都可以利用该格式得到误差可以控制在一定范围内的数值解，从而可以对实际复杂问题进行数值模拟。

附录

差分格式两边同时作内积得：

$\begin{array}{l}\tau {\displaystyle \underset{n=1}{\overset{N}{\sum }}\left({\delta }_{\tau }^{\alpha }\left({\delta }_t{u}_{i,j}^{n-\frac{1}{2}},{\psi }_{i,j}\right),{\delta }_t{u}_{i,j}^{n-\frac{1}{2}}\right)}-\tau {\displaystyle \underset{n=1}{\overset{N}{\sum }}\left({\delta }_x^2{\left(p_{1}u\right)}_{i,j}^{n-\frac{1}{2}},{\delta }_t{u}_{i,j}^{n-\frac{1}{2}}\right)}-\tau {\displaystyle \underset{n=1}{\overset{N}{\sum }}\left({\delta }_y^2{\left(p_{2}u\right)}_{i,j}^{n-\frac{1}{2}},{\delta }_t{u}_{i,j}^{n-\frac{1}{2}}\right)}\\ +\tau {\displaystyle \underset{n=1}{\overset{N}{\sum }}\left({\left(r_1\right)}_{i,j}{\Delta }_x{u}_{i,j}^{n-\frac{1}{2}},{\delta }_t{u}_{i,j}^{n-\frac{1}{2}}\right)}+\tau {\displaystyle \underset{n=1}{\overset{N}{\sum }}\left({\left(r_2\right)}_{i,j}{\Delta }_y{u}_{i,j}^{n-\frac{1}{2}},{\delta }_t{u}_{i,j}^{n-\frac{1}{2}}\right)}+\tau {\displaystyle \underset{n=1}{\overset{N}{\sum }}\left(q_{i,j}{u}_{i,j}^{n-\frac{1}{2}},{\delta }_t{u}_{i,j}^{n-\frac{1}{2}}\right)}\\ =\tau {\displaystyle \underset{n=1}{\overset{N}{\sum }}\left(f_{i,j}^{n-\frac{1}{2}},{\delta }_t{u}_{i,j}^{n-\frac{1}{2}}\right)}\end{array}$ (11)

由引理1得

$\tau {\displaystyle \underset{n=1}{\overset{N}{\sum }}\left({\delta }_{\tau }^{\alpha }\left({\delta }_t{u}_{i,j}^{n-\frac{1}{2}},{\psi }_{i,j}\right),{\delta }_t{u}_{i,j}^{n-\frac{1}{2}}\right)}\ge \frac{t_N^{1-\alpha }}{2}\tau {\displaystyle \underset{n=1}{\overset{N}{\sum }}{\Vert {\delta }_t{u}^{n-\frac{1}{2}}\Vert }^2}-\frac{t_N^{2-\alpha }}{2\left(2-\alpha \right)}{\Vert \psi \Vert }^2.$

由引理2得

$-h_1{h}_2{\displaystyle \underset{j=1}{\overset{m_2-1}{\sum }}{\displaystyle \underset{i=1}{\overset{m_1-1}{\sum }}{\delta }_x^2{\left(p_{1}u\right)}_{i,j}^{n-\frac{1}{2}}{\delta }_t{u}_{i,j}^{n-\frac{1}{2}}}}-h_1{h}_2{\displaystyle \underset{j=1}{\overset{m_2-1}{\sum }}{\displaystyle \underset{i=1}{\overset{m_1-1}{\sum }}{\delta }_y^2{\left(p_{2}u\right)}_{i,j}^{n-\frac{1}{2}}{\delta }_t{u}_{i,j}^{n-\frac{1}{2}}}}=\frac{1}{2\tau }\left({\left|p{u}^n\right|}_1^2-{\left|p{u}^{n-1}\right|}_1^2\right),$

将(11)等式左端四五项移至等式右端，由于 $p_1\left(x,y\right),r_1\left(x,y\right),p_2\left(x,y\right),r_2\left(x,y\right)\in ℂ\left[a,b\right]\times \left[c,d\right]$ ，则存在常数 $C_1=\underset{x\in \left[a,b\right],y\in \left[c,d\right]}{\max }\left\{\frac{r_1\left(x,y\right)}{p_1\left(x,y\right)},\frac{r_2\left(x,y\right)}{p_2\left(x,y\right)}\right\}$ 有

$\begin{array}{c}-\tau {\displaystyle \underset{n=1}{\overset{N}{\sum }}\left({\left(r_1\right)}_{i,j}{\Delta }_x{u}_{i,j}^{n-\frac{1}{2}},{\delta }_t{u}_{i,j}^{n-\frac{1}{2}}\right)}=-\tau {\displaystyle \underset{n=1}{\overset{N}{\sum }}\left({\left(r_1\right)}_{i-\frac{1}{2},j}{\delta }_t{u}_{i-\frac{1}{2},j}^{n-\frac{1}{2}},{\delta }_x{u}_{i-\frac{1}{2},j}^{n-\frac{1}{2}}\right)}\\ =-\tau {\displaystyle \underset{n=1}{\overset{N}{\sum }}\left(\frac{{\left(r_1\right)}_{i-\frac{1}{2},j}}{{\left(p_1\right)}_{i-\frac{1}{2},j}}{\delta }_t{u}_{i-\frac{1}{2},j}^{n-\frac{1}{2}},{\left(p_1\right)}_{i-\frac{1}{2},j}{\delta }_x{u}_{i-\frac{1}{2},j}^{n-\frac{1}{2}}\right)}\\ \le \tau {\displaystyle \underset{n=1}{\overset{N}{\sum }}\left[{\epsilon }_1{C}_1{\Vert {\delta }_t{u}^{n-\frac{1}{2}}\Vert }^2+\frac{1}{8{\epsilon }_1}\left({\Vert p_1{\delta }_x{u}^n\Vert }^2+{\Vert p_1{\delta }_x{u}^{n-1}\Vert }^2\right)\right]},\end{array}$

则有

$\begin{array}{l}-\tau {\displaystyle \underset{n=1}{\overset{N}{\sum }}\left({\left(r_1\right)}_{i,j}{\Delta }_x{u}_{i,j}^{n-\frac{1}{2}},{\delta }_t{u}_{i,j}^{n-\frac{1}{2}}\right)}-\tau {\displaystyle \underset{n=1}{\overset{N}{\sum }}\left({\left(r_2\right)}_{i,j}{\Delta }_y{u}_{i,j}^{n-\frac{1}{2}},{\delta }_t{u}_{i,j}^{n-\frac{1}{2}}\right)}\\ \le \tau {\displaystyle \underset{n=1}{\overset{N}{\sum }}\left[2{\epsilon }_1{C}_1{\Vert {\delta }_t{u}^{n-\frac{1}{2}}\Vert }^2+\frac{1}{8{\epsilon }_1}\left({\left|p{u}^n\right|}_1^2+{\left|p{u}^{n-1}\right|}_1^2\right)\right]},\end{array}$

等式左端第六项可以写作：

$\tau {\displaystyle \underset{n=1}{\overset{N}{\sum }}\left(q_{i,j}{u}_{i,j}^{n-\frac{1}{2}},{\delta }_t{u}_{i,j}^{n-\frac{1}{2}}\right)}=\frac{1}{2}{\Vert q{u}^N\Vert }^2-\frac{1}{2}{\Vert q{u}^0\Vert }^2.$

通过Cauchy-Schwarz不等式放缩等式右端项，有

$\tau {\displaystyle \underset{n=1}{\overset{N}{\sum }}\left(f_{i,j}^{n-\frac{1}{2}},{\delta }_t{u}_{i,j}^{n-\frac{1}{2}}\right)}\le {\epsilon }_2\tau {{\displaystyle \underset{n=1}{\overset{N}{\sum }}\Vert {\delta }_t{u}^{n-\frac{1}{2}}\Vert }}^2+\frac{\tau }{4{\epsilon }_2}{{\displaystyle \underset{n=1}{\overset{N}{\sum }}\Vert f^{n-\frac{1}{2}}\Vert }}^2.$

由于 ${\epsilon }_i\left(i=1,2\right)$ 是任意值，故可以取特定的值将不等式两端的 $\tau {\displaystyle \underset{n=1}{\overset{N}{\sum }}{\Vert {\delta }_t{u}^{n-\frac{1}{2}}\Vert }^2}$ 消去，即取 ${\epsilon }_1=\frac{t_N^{1-\alpha }}{8C_1},{\epsilon }_2=\frac{t_N^{1-\alpha }}{4}$ ，利用Gronwall不等式并且令 $C_2=\frac{2C_1}{t_N^{1-\alpha }},C_3=\frac{2t_N^{1-\alpha }}{2-\alpha }$ ，可以得到

${\left|p{u}^N\right|}_1^2\le {\text{e}}^{8C_{1}T}\left(3{\left|p{u}^0\right|}_1^2+\frac{2C_2}{C_1}\tau {\displaystyle \underset{n=1}{\overset{N}{\sum }}{\Vert f^{n-\frac{1}{2}}\Vert }^2}+C_3{\Vert \psi \Vert }^2+2{\Vert q{u}^0\Vert }^2+4C_1\tau k{M}_0\right),$

其中 $k\le N$ ， $N\tau \le T$ ， $M_0=\max \left\{{\left|p{u}^0\right|}_1^2,\cdots ,{\left|p{u}^{k-1}\right|}_1^2\right\}$ 。