求解线弹性双孔问题的虚拟元方法

Solving the Linear Elastic Porous Problem on Virtual Element Method

摘要: 本文研究虚拟元方法求解线弹性双孔板问题，该方法可以有效解决孔边缘出现的应力集中现象，能够克服线弹性问题的非物理上的压力震荡现象，而且具有剖分过程简单、网格适应性强、可以借助悬点优化边界问题、基函数不需要显式表达、借助特殊的投影算子及自由度求出刚度矩阵的优势，进而奠定了虚拟元方法在处理同类问题的地位。最后通过误差分析和数值实验，证明了虚拟元方法求解线弹性双孔板问题的有效性与可行性，因此，该方法可以为检验耦合杂交混合元、Galerkin法和有限元方法等其它近似方法提供参考。

Abstract: In this paper, the virtual element method is used to study the linear elastic porous plate problem, it can effectively solve the phenomenon of stress concentration at the edge of the hole and overcome the non-physical pressure shock phenomenon of linear elastic problem. Moreover, this method has the advantages of simple subdivision process, strong grid adaptability, optimized boundary problem with suspension points, no explicit expression of basis function, and stiffness matrix obtained with special projection operators and degrees of freedom, thus establishing the position of virtual element method in dealing with similar problems. Finally, through error analysis and numerical experiments, the validity and feasibility of the virtual element method for the problem of linear elastic porous plate are proved. Therefore, the method can provide a reference for testing other approximate methods such as a coupled of hybrid element, Galerkin method and finite element method.

1. 引言

随着科技的迅猛发展，偏微分方程的应用逐渐广泛，在现代学科中发挥着愈发重要的作用，例如材料科学、工程力学及生物科学等方面，而线弹性带孔模型是偏微分方程中非常重要的方程。与材料科学中的新材料制备、工程力学中的合金铸造和生物科学中的图形处理都密不可分。而带孔板是线弹性力学中的经典问题，在车辆、土木、机械、以及航空航天等各类工程结构物中较为常见，具有一定的工程应用价值。在工程实际中由于某种用途，不可避免地需要对板结构开孔，而由于这些孔的存在，使得带孔板在孔口附近的受荷载作用下的应力局部增高，远大于无孔时的应力，从而产生了应力集中现象 [1] 。对于孔来说，由于孔的边缘处应力较大，那么在带孔板受到外界较小的荷载时，孔的边缘出现应力集中现象的区域会发生塑性形变，因此，应力集中区域的应力在结构强度分析中十分关键，所以，获取精确、稳定、可靠的解至关重要。但是由于线弹性带孔板方程耦合复杂的特性，而且开孔区域的几何构型是较为复杂的，将导致存在形态较差的单元，使得分析线弹性带孔板问题的数值解变得比较困难，这也引起了众多中外学者的关注。起初，人们只将位移和压力看作唯一的未知量，使用线性有限元方法处理这种简化的线弹性带孔方程，学者W. H. Yuan提出SPFEM方法 [2] 以及J. Kou提出的DG方法 [3] 也都被广泛应用，但这些方法都无法得到良好的计算精度；后来，有更多的学者开始在原有的两个量的基础上增加流体通量这一未知量，变为三场线弹性带孔模型。这时，使用传统的有限元方法求解这类问题是不够稳定的，会出现闭锁现象，也就是在数值上出现非物理上的压力震荡现象，也就是说在误差估计时得到的常数 $C=0$ ，一般情况下，出现这种现象的前提是线弹性带孔介质的孔隙率 $c_0=0$ ，而C又与物理参数 $c_0$ 有关，从而误差会变得非常大，所以数值求解结果将与实际结果相脱离。因此，研究线弹性带孔问题的关键就是克服闭锁现象，也就是要消除这种非物理的压力震荡，继而众多学者提出一些稳定化方法，Hu等人提出Biot模型的非协调有限元方法 [4] 、Yi等人提出耦合非协调有限元方法 [5] 、Niu等人提出基于Galerkin有限元方法和耦合杂交混合元方法 [6] 、交错网格有限差分方法求解稳态多孔模型 [7] 等，但是所面对的是剖分困难，而且基函数的求解起来较为繁琐，因此找到一种有效的数值求解方法至关重要。

本文选用虚拟元方法 [8] [9] 处理线弹性双孔方程，首先，对于计算域的分解可以采用虚拟元方法中非常一般且有效的方法来完成，即凸多边形。其次，构造局部虚拟元空间以及全局虚拟元空间，选择合适的自由度，并做出相应的投影算子，将原空间投影到可计算的空间上，进而求解局部刚度矩阵以及质量矩阵，从而在不需要计算剖分单元的内部基函数的前提下求得数值解。最后，通过二维线弹性双孔板方程的数值计算，证明了理论分析结果的正确性。

本文在第2节给出了虚拟元方法对于二维线弹性双孔模型的理论分析。第3节给出二维线弹性双孔板方程，通过数值实验验证理论分析结果的正确性。第4节对本文进行了总结和展望。

2. 线弹性双孔板的虚拟元方法

2.1. 问题模型

在本文中，我们将遵循通常的Sobolev空间和范数的常用符号。假设 $\Omega$ 是二维或三维空间中的一个任意开集，并且它的边界是分段光滑的，即满足Lipschitz连续，那么任取 $\Omega$ 上的函数 $u\left(x\right)$ ,定义 $u\left(x\right)$ 的勒贝格积分为 ${\displaystyle {\int }_{\Omega }u\left(x\right)\text{d}x}$ ；用 ${\Vert \cdot \Vert }_{s,\Omega }$ 和 ${\left|\cdot \right|}_{s,\Omega }$ 分别表示Sobolev空间 $H^s\left(\Omega \right)$ 的范数和半范数，用 ${\left(\cdot ,\cdot \right)}_{s,\Omega }$ 表示空间 $H^s\left(\Omega \right)$ 的相应的内积，则对于任意的q，定义范数 ${\Vert \cdot \Vert }_{s,\Omega }$ 为

${\Vert u\Vert }_{s,\Omega }={\left({\displaystyle \underset{i=0}{\overset{s}{\sum }}{\left|u\left(x\right)\right|}_{i,\Omega }^q}\right)}^{\frac{1}{q}}$

定义半范数 ${\left|\cdot \right|}_{s,\Omega }$ 为

${\left|u\right|}_{s,\Omega }={\left({\displaystyle \underset{\alpha }{\sum }{\displaystyle {\int }_{\Omega }{\left|{\partial }^{\alpha }u\left(x\right)\right|}^q\text{d}\Omega }}\right)}^{\frac{1}{q}}$

其中 $\alpha =\left({\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_n\right)$ ， $\left|\alpha \right|={\alpha }_1+{\alpha }_2+\cdots +{\alpha }_n$ ， ${\partial }^{\alpha }=\underset{i=1}{\overset{n}{{\displaystyle \prod }}}{\partial }^{{\alpha }_i}$ 。特别地，当 $s=0$ 时， $H^0\left(\Omega \right)$ 空间就是 $L^2\left(\Omega \right)$ 空间，该空间上的范数、半范数和内积分别定义为 ${\Vert \cdot \Vert }_{\Omega }$ 、 ${\left|\cdot \right|}_{\Omega }$ 和 ${\left(\cdot ,\cdot \right)}_{\Omega }$ 。

特别地，在给定边界条件下，考虑线弹性在体积荷载作用下的变形问题，设 $\lambda$ 和 $\mu$ 为Lamé系数， $f\in {\left(L^2\left(\Omega \right)\right)}^2$ 为向量值函数， $\Gamma$ 为区域的边界，为简单起见，本文考虑最基础的Dirichlet边界条件。定义线弹性双孔方程：

$\{\begin{array}{ll}{c}_{0}p+\alpha \nabla \cdot u-\nabla \cdot \left(k\nabla p\right)=g,\hfill & u\in \Omega ,\hfill \\ -\left(\lambda +\mu \right)\nabla \left(\nabla \cdot u\right)-\mu {\nabla }^{2}u+\alpha \nabla p=f,\hfill & u\in \Omega ,\hfill \\ -k\nabla p\cdot n=0,\hfill & u\in \partial \Omega ,\hfill \\ u=0,\hfill & u\in \partial \Omega ,\hfill \end{array}$ (1)

其中f为体积力荷载， $n$ 为边界上的单位外法线向量。接下来定义容许位移空间，

$\{\begin{array}{l}V:={\left(H_0^1\left(\Omega \right)\right)}^2,\\ {\Vert v\Vert }_V^2:={\Vert \nabla v\Vert }_{{\left(L^2\left(\Omega \right)\right)}^4},\end{array}\forall v\in V.$

定义双线性形式如下，

$a\left(u,v\right):=2\mu {\displaystyle {\int }_{\Omega }\epsilon \left(u\right):\epsilon \left(v\right)\text{d}x}+\lambda {\displaystyle {\int }_{\Omega }\text{div}u\text{div}v\text{d}x}\equiv 2\mu a_{\mu }\left(u,v\right)+\lambda a_{\lambda }\left(u,v\right)$

其中表示对称梯度算子， $\lambda =\frac{E\nu }{\left(1+\nu \right)\left(1-2\nu \right)}$ ， $\mu =\frac{E}{2\left(1+\nu \right)}$ ，E叫做弹性模量， $\nu$ 是泊松比。

定义椭圆算子 $A_{\lambda ,\mu }$ ，

$A_{\lambda ,\mu }u:=-\left(\begin{array}{c}2\mu \left(u_{1,xx}+\frac{1}{2}\left(u_{1,yy}+u_{2,xy}\right)\right)+\lambda \left(u_{1,xx}+u_{2,yx}\right)\\ 2\mu \left(\frac{1}{2}\left(u_{1,yx}+u_{2,xx}\right)+u_{2,yy}\right)+\lambda \left(u_{1,xy}+u_{2,yy}\right)\end{array}\right).$

显然，通过Korn不等式，双线性形式有如下限制，

$\alpha {\Vert v\Vert }_V^2\le a\left(v,v\right)\le M{\Vert v\Vert }_V^2\forall v\in V.$

其中 $M>0$ ， $\alpha >0$ ，是两个只与 $\Omega$ ， $\lambda$ 和 $\mu$ 有关的常数。

对于 $f\in V^{\prime }$ ，定义对偶积为 $\langle f,v\rangle$ ，它是传统的 ${\left(L^2\right)}^2$ 内积，因此(1)式的双线性形式变为

$a\left(u,v\right)=\langle f,v\rangle \forall v\in V.$ (2)

由Lax-Milgram定义可知，问题(2)的解存在且唯一。

定义 $W$ 为容许变化空间， $W\subseteq {\left(C^0\left(\bar{\Omega }\right)\right)}^2$ ，所以问题(2)等价于

$\{\begin{array}{ll}{A}_{\lambda ,\mu }u=f\hfill & u\in \in \Omega ,\hfill \\ u=0\hfill & u\in \Gamma .\hfill \end{array}$

综上，连续问题(1)已转化为相应的变分形式，正因为良好的近似性是虚拟元方法的优势之一，即在区域中任意离散剖分单元上建立完整的求解过程，进而通过加权求和的方式求得原问题的近似解，所以，本文接下来将考虑单元上问题的离散形式。

2.2. 离散问题

定义虚拟元空间：对于区域 $\Omega$ 的剖分集 ${\mathcal{T}}_h$ 中的每一个剖分单元K，当 $k\ge 1$ 时，有

$V_h=\left\{v\in H^1:v_{|E}\in V_h^K,v_{|\partial K}\in {\mathbb{P}}_k\left(\partial K\right),K\in {\mathcal{T}}_h\right\},$

其中 $V_h^K$ 是剖分单元K上的局部虚拟元空间，定义如下

$V_h^K:=\left\{v\in H^1\left(K\right):v_{|\partial K}\in C^0\left(\partial K\right)\right\}.$

为了得到问题(2)的近似解，将区域 $\Omega$ 剖分为多边形单元K的集合 ${\left({\mathcal{T}}_h\right)}_h$ ，对 ${\mathcal{T}}_h$ 做如下的正则性条件假设。

· 剖分 ${\mathcal{T}}_h$ 是由有限数量的简单多边形构成的，这些多边形可以是凸或非凸的；

· 剖分单元E是相对于半径不小于 $r{h}_E$ 的圆的每一点都是星形的；

· 剖分单元E的最短边 $h_s$ 与最大直径 $h_E$ 之比大于r，即 $h_s\ge r{h}_E$ ；

定义离散范数和离散的双线性形式如下，

$\begin{array}{l}{\Vert v\Vert }_V^2={\displaystyle \underset{K\in {\mathcal{T}}_h}{\sum }{\Vert v\Vert }_{V,K}^2}\forall v\in V,\\ a\left(u,v\right)={\displaystyle \underset{K\in {\mathcal{T}}_h}{\sum }{a}^K\left(u,v\right)}\forall u,v\in V.\end{array}$

紧接着，给出单元K上的局部离散的双线性形式，

$a_h\left(u_h,v_h\right)={\displaystyle \underset{K\in {\mathcal{T}}_h}{\sum }{a}_h^K\left(u_h,v_h\right)}\forall u_h,v_h\in V_h.$

显然，双线性形式满足如下一致性和稳定性条件：

· 一致性： $\forall v_h\in V_h$ ， $\forall p\in {\mathbb{P}}_k\left(K\right)$ ，有

$a_h\left(p,v_h\right)=a_h^K\left(p,v_h\right).$

· 稳定性：存在两个正的常数 ${\alpha }_{*}$ 和 ${\alpha }^{*}$ ，它们独立于h和K， $\forall v_h\in V_h^K$ 使得

${\alpha }_{*}{a}^K\left(v_h,v_h\right)\le a_h^K\left(v_h,v_h\right)\le {\alpha }^{*}{a}^K\left(v_h,v_h\right).$

上述一致性的要求是为了满足工程问题中常用的预设配置测试(patch test)，证明了当解是一个关于网格的分段线性多项式时，该方法是精确的。另一方面，从证明中可以发现，稳定性保证了离散双线性形式继承了原变分形式的连续性。

首先，对于每一个单元K上的函数 $v_h$ 的值，需要借助单元K上的自由度，如下

$\{\begin{array}{l}•v_h在单元E的每个顶点处的函数值,\hfill \\ •v_h在每条边e上k+1个\text{Gauss-Lobatto}求积点的k-1个内点的函数值,\hfill \\ •\Delta v_h在单元E上是k-2阶矩,即{\left|E\right|}^{-1}{\displaystyle {\int }_E{v}_h{m}_{\alpha }},\alpha =1,\cdots ,n_{k-2}.\hfill \end{array}$

所以，对于 $p\in {\left({\mathbb{P}}_K\right)}^2$ ， $v_h\in V_h^K$ ，有

$a_{\mu }^K\left(p,v_h\right)={\displaystyle {\int }_K\epsilon \left(p\right):\epsilon \left(v_h\right)\text{d}x}=-{\displaystyle {\int }_{K}div\left(\epsilon \left(p\right)\right)\cdot v_h\text{d}x}+{\displaystyle {\int }_{\partial K}\left(\epsilon \left(p\right)\cdot n\right)\cdot v_h\text{d}s}.$ (3)

其中， $div\left(\epsilon \left(p\right)\right)\in {\left({\mathbb{P}}_{k-2}\right)}^2$ ，有

${\displaystyle {\int }_{K}div\left(\epsilon \left(p\right)\right)\cdot v_h\text{d}x}={\displaystyle {\int }_{K}div\left(\epsilon \left(p\right)\right)\cdot {\Pi }_{k-2}^K{v}_h\text{d}x}.$

其中， ${\Pi }_{k-2}^K$ 是 $V_h$ 上的投影算子， ${\Pi }_{k-2}^K{v}_h$ 的值根据自由度计算的，所以(3)式的第一项是可以计算的，第二项中，由于 $v_h$ 在边 $\partial K$ 上的值是可知的，因此，式(3)是可计算的。同样的，

$a_{\lambda }^K\left(p,v_h\right)={\displaystyle {\int }_K\text{div}\left(p\right)\text{div}\left(v_h\right)\text{d}x}=-{\displaystyle {\int }_K\nabla \left(div\left(p\right)\right)\cdot v_h\text{d}x}+{\displaystyle {\int }_{\partial K}\left(div\left(p\right)\cdot v_h\right)\cdot n\text{d}s}.$

知道 $v_h$ 在边 $\partial K$ 上的值，以及根据自由度可知 ${\Pi }_{k-2}^K{v}_h$ 的值，上式同样是可计算的。

为了离散右端项，定义 $L^2$ 投影算子， ${\Pi }_{\bar{k}}^K:V_k\left(E\right)\to {\mathbb{P}}_K\left(E\right)$ ，

$f_h={\Pi }_{\bar{k}}^{K}f,\bar{k}=\max \left\{k-2,0\right\}.$

当 $k\ge 2$ ，右端项的局部离散形式为，

$\langle f_h,v_h\rangle ={\displaystyle \underset{K\in {\mathcal{T}}_h}{\sum }{\displaystyle {\int }_K{f}_h\cdot v_h}\text{d}x}\equiv {\displaystyle \underset{K\in {\mathcal{T}}_h}{\sum }{\displaystyle {\int }_K{\Pi }_{k-2}^{K}f\cdot v_h}\text{d}x}={\displaystyle \underset{K\in {\mathcal{T}}_h}{\sum }{\displaystyle {\int }_{K}f\cdot {\Pi }_{k-2}^K{v}_h}\text{d}x}$

所以，本文要解决的离散问题可以写成： $\forall v_h\in V_h^E$ ，找到 $u_h\in V_h$ ，满足

$a_h\left(u_h,v_h\right)=\langle f_h,v_h\rangle .$ (4)

2.3. 误差分析

定理1 [10] 对于任意凸区域 $\Omega$ ，且 $k\ge 2$ ，对于 $u$ 的每一个分段逼近 $u_{\pi }$ ， $u_{\pi }\in {\left({\mathbb{P}}_k\right)}^2$ ，有

${\Vert u-u_h\Vert }_{0,\Omega }\le Ch\left({\Vert u-u_h\Vert }_V+{\Vert u-u_{\pi }\Vert }_{h,V}+h^{k-2}{\Vert f-f_h\Vert }_{0,\Omega }\right),$

其中，常数C仅与 $\Omega$ ， $\lambda$ ， $\mu$ ， ${\alpha }^{*}$ 有关。

定理2对于任意凸区域 $\Omega$ ，u是问题(1)的真解，u是问题(4)的近似解，有

${\Vert u-u_h\Vert }_{0,\Omega }\le C{h}^{k+1}{\left|u\right|}_{k+1,\Omega },$

证明：当 $k=1$ 时，假定右端项的积分次数至少是一阶的，结合定理1，那么

$\begin{array}{c}{\Vert u-u_h\Vert }_{0,\Omega }\le Ch\left({\Vert u-u_h\Vert }_V+{\Vert u-u_{\pi }\Vert }_{h,V}+{\Vert f-f_h\Vert }_{0,\Omega }+h{\Vert f\Vert }_{0,\Omega }\right)\\ \le C{h}^2{\left({\left|u\right|}_{2,\Omega }^2+{\displaystyle \underset{K\in {\mathcal{T}}_h}{\sum }{\left|f\right|}_{1,K}^2}\right)}^{1/2},\end{array}$

在 $u$ 是足够正定时，最后一项的估计是成立的。

当 $k=2$ 时，我们希望 $L^2$ 范数的收敛误差能达到 ${\rm O}\left(h^{k+1}\right)$ ，所以，对于任意 $v_h\in V_h$ ， $K\in {\mathcal{T}}_h$ ，定义局部函数的平均值，

${\bar{v}}_h=\frac{{\displaystyle {\int }_K{v}_h\text{d}x}}{\left|K\right|},\overline{\nabla v_h}=\frac{{\displaystyle {\int }_K\nabla v_h\text{d}x}}{\left|K\right|},$

上式可以利用 $V_h$ 的自由度结合分部积分精确计算。

因此，定义剖分单元K中的重心坐标表示为 $x_B$ ，定义

$\begin{array}{l}{\tilde{v}}_h={\bar{v}}_h+\overline{\nabla v_h}\cdot \left(x-x_B\right),\\ \langle f_h,v_h\rangle ={\displaystyle \underset{K\in {\mathcal{T}}_h}{\sum }{\displaystyle {\int }_K{\Pi }_1^{K}f\cdot {\tilde{v}}_h\text{d}x}}.\end{array}$

所以，有

$\begin{array}{c}\langle f_h-f,v_h\rangle ={\displaystyle \underset{K\in {\mathcal{T}}_h}{\sum }{\displaystyle {\int }_K\left({\Pi }_1^{K}f\cdot {\tilde{v}}_h-f\cdot v_h\right)\text{d}x}}\\ ={\displaystyle \underset{K\in {\mathcal{T}}_h}{\sum }{\displaystyle {\int }_K\left({\Pi }_1^{K}f\cdot \left({\tilde{v}}_h-v_h\right)+\left({\Pi }_1^{K}f-f\right)\cdot v_h\right)\text{d}x}}\\ ={\displaystyle \underset{K\in {\mathcal{T}}_h}{\sum }{\displaystyle {\int }_K\left(\left({\Pi }_1^{K}f-{\Pi }_0^{K}f\right)\cdot \left({\tilde{v}}_h-v_h\right)+\left({\Pi }_1^{K}f-f\right)\cdot \left(v_h-{\tilde{v}}_h\right)\right)\text{d}x}}\\ \le C{\displaystyle \underset{K\in {\mathcal{T}}_h}{\sum }\left({\Vert {\Pi }_1^{K}f-{\Pi }_0^{K}f\Vert }_{0,K}+{\Vert {\Pi }_1^{K}f-f\Vert }_{0,K}\right){\Vert {\tilde{v}}_h-v_h\Vert }_{0,K}}\\ \le C{h}^3{\left({\displaystyle \underset{K\in {\mathcal{T}}_h}{\sum }{\left|f\right|}_{1,K}^2}\right)}^{1/2}{\left|v_h\right|}_{2,K}.\end{array}$

3. 数值实验

本文考虑线弹性双孔元件模型，考虑长方形区域 $\Omega =\left[-18,18\right]\times \left[-13,13\right]$ ，假定系数分别为： $k=1$ ， $\lambda =1$ ， $\mu =1$ ， $E=3\times {10}^7$ ， $\nu =0.3$ ，取两个半径长度不同的孔，双孔中的左侧孔半径为 $r_{left}=4$ ，右侧孔半径为 $r_{right}=5$ ，这样做的目的是为了后面进一步验证本方法的鲁棒性。取真解函数 $u$ ，p分别为

$\{\begin{array}{l}p=\cos \pi y,\hfill \\ u=\left(\begin{array}{c}xy\left(1-x\right)\left(1-y\right)\\ xy\left(1-x\right)\left(1-y\right)\end{array}\right).\hfill \end{array}$

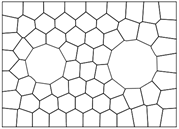
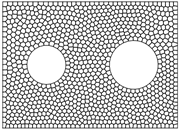
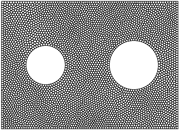
接下来，对区域进行剖分，图1给出区域 $\Omega$ 的四种不同数量的网格剖分，其中网格剖分数N分别为64、256、1024、4096。

(a) $N=8\times 8$ (b) $N=16\times 16$ (c) $N=32\times 32$ (d) $N=64\times 64$

Figure 1. Grid division diagram

图1. 网格剖分图

图2给出四种不同网格下，应用虚拟元方法所得的位移与应力的数值解。

Figure 2. Numerical solution of displacement and stress corresponding to different mesh numbers

图2. 不同网格数对应的位移与应力的数值解

对应的误差及收敛阶见表1。从表中可以看出，利用虚拟元方法所求的误差结果与理论分析中的收敛性分析是一致的，均可达到最优收敛阶。

Table 1. Error and error order corresponding to different mesh numbers

表1. 不同网格数对应的误差及误差阶

4. 总结与展望

在本文的工作中，我们提出虚拟元方法求解线弹性双孔体模型，在文章的第一部分中介绍了该问题模型的研究背景、意义、前人所做工作以及所遇到的困难，进而确定选用虚拟元方法研究该问题的优势以及意义。在第二部分中，我们详细阐述了对于线弹性双孔问题的连续问题转化为离散问题，明确解的存在唯一性，强调全局双线形式与局部双线性形式的一致性和稳定性，给出虚拟元方法处理该问题的误差分析并详细证明。在第三部分中，我们通过数值实验验证了数值近似结果与理论分析相一致，通过改变剖分单元数量，计算出数值结果并绘制出数值解图，通过误差表可知，在使用虚拟元方法解决该问题具有较强的鲁棒性，对孔距之间的距离变化并不敏感，且误差收敛速度达到最优阶，进而说明理论分析的正确性以及有效性。对于线弹性孔板问题的虚拟元方法仍存在许多问题有待解决，例如非协调线弹性多孔板问题、带时间项的线弹性多孔板问题等，未来将成为我们主要研究的方向。

参考文献

NOTES

^*通讯作者。