1. 引言
自20世纪90年代以来,随机非线性系统的镇定问题得到了广泛的研究。与渐近稳定系统 [1] [2] [3] 相比,有限时间稳定系统具有更快的收敛速度、更高的精度和更好的抗干扰能力 [4] [5] 。因此,在过去的几十年里,有限时间稳定问题受到了各个研究领域学者的广泛关注。例如,Yin等人 [6] 解决了随机非线性系统的有限时间稳定性问题,在 [7] 中研究了严格反馈形式下随机非线性系统的有限时间稳定性。Zhai等人 [8] 利用状态反馈研究了一类随机非线性系统的全局有限时间镇定,在 [9] 中研究了随机高阶非线性系统的有限时间输出反馈镇定。此外,有限时间控制已应用于航天器系统 [4] 和机械系统 [10] 。
同时,具有马尔可夫切换的系统也引起了广泛的关注。因为马尔可夫切换系统常被用来描述许多物理系统,这些物理系统经常发生不可预测的结构变化,如随机故障、突然的环境扰动、非线性物体上工作点的突然变化等 [11] 。Mao [12] 研究了具有马尔可夫切换的一般随机非线性微分方程的指数稳定性。Zhao和Liu [13] 建立了弱解框架下非局部利普希茨随机时变非线性系统的随机有限时间稳定性理论,研究了一类具有马尔可夫切换的随机高阶非线性系统的有限时间镇定问题,并利用所提出的理论严格分析了闭环系统弱解的存在性和有限时间稳定性。事实上,马尔可夫切换已被广泛用于模拟许多真实系统,如生物系统、制造系统和人口系统 [14] [15] 。
同时,由于随机逆动力学被广泛应用于各种工程应用中,影响着实际控制系统的性能,其研究一直在控制理论和技术的发展中发挥着重要作用。Tsinias [16] 和Tang等人 [17] 分别提出了随机输入状态稳定性(SISS)的概念。Zhao等人 [18] 发展了随机有限时间稳定性理论,研究了具有逆动力学的非局部利普希茨随机非线性系统弱解意义上的有限时间稳定性。但是到目前为止,对于具有随机逆动力学的马尔可夫切换随机非线性系统,还没有得到有限时间稳定性的结果。本文给出了具有随机逆动力学的马尔可夫切换随机低阶非线性系统的有限时间稳定性定理,并求解了该系统的有限时间镇定问题。主要贡献如下:
1) 就作者所知,对于具有随机逆动力学的马尔可夫切换随机低阶非线性系统,还没有研究过有限时间的镇定问题。
2) 与随机高阶系统相比,我们考虑了一类
的随机低阶系统。这两类系统的根本区别请见文献 [19] 的注释2。
本文组织结构如下,在第2节中,我们介绍了一些预备知识和引理;第3节中给出状态反馈控制器的设计和分析;第4节给出了数值模拟实例;第5节给出结论。
2. 预备知识
本文将使用以下符号。
表示所有非负实数的集合;
表示实n维空间;
为
实矩阵空间;对于给定的向量或矩阵Z,
表示它的转置,
表示Z为方阵时的迹;
表示内积;
表示欧几里得向量范数和F-范数;S表示集合
;
表示
上的所有非负函数
在x上连续二次可微;K表示所有函数的集合:
,它们是连续的,严格递增且在零处消失;
表示K类且无界的所有函数的集合。
考虑下面具有马尔可夫切换的随机系统:
(1)
其中
和
是博雷尔可测的,
是分布具有紧支撑的随机变量,
是概率空间上的随机变量。
假设1
是在S上取值且在概率空间上右连续的马尔可夫链,其生成器
由下面的式子给定
(2)
其中,
,
是相对于
的高阶无穷小。这里,如果
时,有
则
是i到j的转移率。
定义1 [13] 如果在概率空间
上存在连续随机过程
,其过滤
满足通常条件,一个满足
的m维
-自适应的布朗运动
和一个在
上
-自适应的马尔可夫链
使得(i)
有给定的分布,(ii)
有给定的初始分布和转移函数,(iii)对
,
a.s.和
a.s.,(iv)
(3)
则对
,
或
叫做系统(1)的全局弱解。
定义2 [13] 对任意给定的
,与(1)相关联的算子
定义为
(4)
定义3 [13] 如果对于系统(1)的任意全局弱解
,简单记为
,有以下情况成立:
i) 依概率有限时间吸引:第一次撞击时间
,也就是所谓的随机停时,是几乎处处有限的,即
;
ii) 依概率稳定:
,存在一类K函数
使得
。
那么称系统(1)的平凡弱解是全局依概率有限时间稳定的。
考虑下面的系统:
(5)
其中
,
,
,令
,
,
。
定理1 对每一
,假设
和
在
上是联合连续的。如果存在两个函数
,
和
函数
,
,
,
,常数
,
使得对所有的
,
有
(6)
(7)
(8)
那么系统(1)存在弱解并且系统(5)的平凡弱解是依概率有限时间稳定的。
证明:参考文献 [13] ,我们可以证明弱解的存在性并且构造(5)的近似解,然后用文献 [18] 的方法证明定理的全局依概率有限时间稳定性。
引理1 [20] 对任意实数y和
,有下面的不等式成立
(9)
引理2 [21] 设q是一个奇数,则有下面的不等式成立
(10)
(11)
引理3 [22] 假设n和m是正实数,
和
是连续函数。那么对任意常数
,
(12)
3. 有限时间镇定
3.1. 问题表述
考虑由下列带有马尔可夫切换的随机微分方程描述的系统:
(13)
其中
,是不可测的随机逆动态;
是系统状态;
是控制输出,
;对
,
,
;
是一个奇分数;
是一个m维布朗运动;
是一个在概率空间上满足假设1的马尔可夫链;对
,
,
,
,
,是博雷尔可测函数;在这个部分,假设马尔可夫链
与布朗运动
无关。
假设2 系统的低阶满足
。
假设3
,
,
,
。对每一个
,
,
,
,
,
的系数是关于z和x连续的。
假设4 如果存在一个函数
,
函数
,
,
,常数
,
,使得对所有
,有
(14)
(15)
另外,存在已知光滑函数
和
使得对任意
有
和
。
假设5 对每一个
,
,存在已知的在原点消失的光滑非负函数
和
和关于
的光滑非负函数
和
使得
(16)
(17)
3.2. 设计状态反馈控制器
第1步:选择
和
。由定义2和引理3可得
(18)
其中
,
是正常数,
和
是光滑非负函数,
,
。替换第一个虚拟控制器
,其中
是一个光滑函数,代入(18)式有
(19)
其中
,
是一个设计好的非负光滑函数。
命题1 假设在
步,有一个
,正定且径向无界函数
以及一系列虚拟控制器
定义为
(20)
使得
(21)
其中
,
是光滑函数,
,
,
,
是正常数。接下来说明存在
、正定且径向无界的函数
,及一个虚拟控制器
,使得
(22)
其中
,且
为光滑正函数。
证明:参考文献 [19] 的附录即可得到证明结果。
最后一步:选择
,我们可以得到下面的控制器
(23)
使得
(24)
其中
,
是定义于(20)式。
3.3. 有限时间稳定性分析
引理4 对于假设4中给定的函数
,
,
,
。如果有
(25)
和
(26)
其中定义于
的连续非负递增函数
和
满足
(27)
则存在一个
的非递减的正函数
,使得对
,有
(28)
其中
,
。
证明:在文献 [23] 中,
需要是
函数,但是这个要求在其引理1中没有用到,所以引理4可直接由文献 [23] 中的引理1证得。即得证。
定理2 对于假设4中给定的函数
并且定义
。假设3~5和引理4中的条件成立,那么由(13)和(23)组成的闭环系统有一个全局弱解
且其平凡解是全局依概率有限时间稳定的。
证明:对于定义于引理4中的非递减的正函数
,令
(29)
定义
,接下来参考文献 [23] 定理2的证明可以得到
(30)
其中
。
令
(31)
通过(24)和
(32)
我们有
(33)
注意
,我们可以构造一个连续非递减的函数
使得
(34)
因此,我们由(33),(34)和引理4可得
(35)
又因为
是一个递增函数,其中
,所以我们有
(36)
其中
。
和
的构式以及和假设4表明
和
是正定且径向无界的。那么根据文献 [24] 中的引理4.3,存在
使得
(37)
同理,存在
使得
(38)
因此,根据定理1,闭环系统(13),(23)有一个弱解。根据定理1,闭环系统(13),(23)的平凡解是依概率有限时间稳定的。即得证。
4. 数值模拟实例
在这个部分,我们将给出一个例子来说明我们在第3节中获得的结果的有效性。考虑下面的系统
(39)
其中
,
,
是1维布朗运动,
是在完全概率空间上具有稳定保守
-矩阵
的右连续齐次马尔可夫链,
是状态空间,
,
,
,
,
,
,
,
,
。假设2和假设5成立。
根据第3节中的方法,我们构建李雅普诺夫函数
并且设计控制器
(40)
其中选择
,初始值
以及由
,
,
,
,
,
,
,
和
给定的
。图1展示了马尔可夫链的轨迹和闭环系统(39),(40)的轨迹。
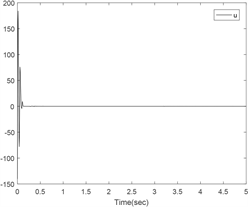
Figure 1. Trajectory of the Markov chain and trajectories for the closed-loop system (39)~(40)
图1. 马尔可夫链的轨迹和闭环系统(39)~(40)的轨迹
5. 结论
我们研究了一类具有随机逆动态的马尔可夫切换随机低阶非线性系统的有限时间控制问题。通过改变能量函数,构造了包括可控系统和随机逆动态在内的整个系统的李雅普诺夫函数,并通过相关随机非线性系统的有限时间稳定性定理,证明了闭环系统是全局依概率有限时间稳定的。