具有恐惧效应与群体防御及捕食者种内竞争的捕食者–食饵动力学

Predator-Prey Dynamics with Fear Effects and Group Defense and Intraspecific Competition by the Predator

摘要: 研究食饵具有恐惧效应和群体防御与捕食者种内竞争的捕食者–食饵模型，分析了系统内部平衡点的存在性以及一定条件下平衡点的稳定性，找出了系统在边界平衡点发生跨临界分岔的条件，并利用Dulac判别法证明了系统在一定条件下不存在极限环。

Abstract: In this paper, we study a prey with fear effect and group defense and predator species competition predator-prey model, analyze the existence of the system and the stability of the equilibrium point, find out the conditions of the transcritical bifurcation at the boundary equilibrium point, and use the Dulac discrimination to prove that the system has no limit ring under certain conditions.

1. 引言

捕食者–食饵的相互作用是生态系统中的一种自然现象，掌握它们之间的动力学行为，对于维持生态系统的平衡有重要作用。捕食关系在生物界中普遍存在，大多数学者认为捕食者通过直接捕食来影响食饵的种群密度 [1] [2] [3] ，但随着生态学的发展，我们发现食饵表现出不同类型的反捕食者行为来对抗它们的捕食者，如栖息地迁移 [4] [5] [6] ，降低繁殖率 [7] [8] [9] ，改变觅食行为 [10] [11] [12] [13] 等，捕食的恐惧效应可以间接的从多方面对食饵种群的种群密度产生影响，Wang等 [14] 首次提出了一个具有恐惧效应的捕食模型，在捕食模型中引入恐惧因子：

$a\left(x\right)=\frac{1}{1+ky}$ , (1.1)

2011年Ajraldi [15] 等人考虑了食饵具有群体防御的捕食系统，2012年Braza [16] 使用一个修正的Lotka-Volterra交互作用项作为功能反应函数对捕食者–食饵系统的动力学行为进行了研究，其模型如下：

$\{\begin{array}{l}\frac{\text{d}x}{\text{d}t}=x\left(1-x\right)-\sqrt{x}y,x\left(0\right)>0\hfill \\ \frac{\text{d}y}{\text{d}t}=-sy+c\sqrt{x}y,y\left(0\right)>0\hfill \end{array}$ , (1.2)

另一方面，气候环境或猎物数量的变化都可能引起捕食者种群的种内竞争 [17] [18] [19] ，即同一种群对共同所需资源的竞争，种内竞争可以起到调节物种的数量的作用。结合上述研究，本文在模型(1.2)的基础上引入恐惧因子及捕食者种内竞争，并对模型进行简化得

$\{\begin{array}{l}\frac{\text{d}x}{\text{d}t}=\frac{x\left(1-x\right)}{1+\theta y}-\sqrt{x}y=xf\left(x\right),x\left(0\right)>0\hfill \\ \frac{\text{d}y}{\text{d}t}=-sy+c\sqrt{x}y-k{y}^2=yg\left(y\right),y\left(0\right)>0\hfill \end{array}$ , (1.3)

其中x表示食饵种群密度，y表示捕食者种群密度，θ为恐惧效应参数，s是捕食者的死亡率，c是生物量转换或消耗率，k表示种内竞争系数，假设初始条件为 $\pi \left(0\right)=\left(x\left(0\right),y\left(0\right)\right)$ ，所有参数均非负。

系统(1.3)的线性化矩阵为

$J\left(x,y\right)=\left[\begin{array}{cc}\frac{1-2x}{1+\theta y}-\frac{y}{2\sqrt{x}}& -\frac{\sqrt{x}\left(1-x\right)}{{\left(1+\theta y\right)}^2}-\sqrt{x}\\ \frac{cy}{2\sqrt{x}}& -s+c\sqrt{x}-2ky\end{array}\right]$ .

2. 解的正性与有界性

定理1 在初始条件 $\pi \left(0\right)=\left(x\left(0\right),y\left(0\right)\right)$ 下，对任意的 $t>0$ ，系统(1.3)的解是正的且一致有界。

证明 显然系统(1.3)在区域 $x>0,y>0$ 上是连续的，且满足Lipschitz条件，由解的存在唯一性定理，系统(1.3)的解 $\left(x,y\right)$ 在 $\left(0,\eta \right)$ 上存在且唯一，其中 $0<\eta <+\infty$ 。由常数变易法，系统(1.3)满足：

$\begin{array}{c}x\left(t\right)=x\left(0\right)\exp {\displaystyle {\int }_0^{t}f\left(s\right)\text{d}s>0}\\ y\left(t\right)=y\left(0\right)\exp {\displaystyle {\int }_0^{t}g\left(s\right)\text{d}s>0}\end{array}$ , (2.1)

因此，当 $x\left(0\right)>0$ ， $y\left(0\right)>0$ 时，对于 $t\ge 0$ ， $x\left(t\right)>0$ ， $y\left(t\right)>0$ 成立。另一方面，由于

$\frac{\text{d}x}{\text{d}t}=\frac{x\left(1-x\right)}{1+\theta y}-\sqrt{x}y\le x\left(1-x\right)$ , (2.1)

因此 $\underset{t\to \infty }{\lim }\sup x\left(t\right)=1$ ，令 $W\left(t\right)=x\left(t\right)+\frac{y\left(t\right)}{c}$ ，则

$\frac{\text{d}W}{\text{d}t}+sW=\frac{x\left(1-x\right)}{1+\theta y}+sx-\frac{k}{c}{y}^2\le \left(1+s\right)x-x^2\le \frac{{\left(1+s\right)}^2}{4}$ , (2.2)

由Growall不等式 [20] ，得到

$0\le W\left(t\right)\le W\left(0\right){\text{e}}^{-st}-\frac{{\left(1+s\right)}^2}{4}{\text{e}}^{-st}+\frac{{\left(1+s\right)}^2}{4}$ , (2.3)

即 $\underset{t\to \infty }{\lim }W\left(t\right)=\frac{{\left(1+s\right)}^2}{4}$ ，因此，系统(1.3)的所有解都将进入区域 $\Omega =\left\{x\left(t\right),y\left(t\right)|0<W\left(t\right)<\frac{{\left(1+s\right)}^2}{4}\right\}$ 内。

3. 平衡点及极限环分析

显然，系统(1.3)的平衡点 $E_0\left(0,0\right),E_1\left(1,0\right)$ 总是存在的，接下来对内部平衡点的存在性进行分析。系统(1.3)内部平衡点的存在性等价于

$\{\begin{array}{c}\frac{\left(1-x\right)}{1+\theta y}-\frac{y}{\sqrt{x}}=f\left(x\right)=0\\ -s+c\sqrt{x}-ky=g\left(y\right)=0\end{array}$ , (3.1)

首先令 $g\left(y\right)=0$ ，有 $y=\frac{-s+c\sqrt{x}}{k}$ ，则当 $\sqrt{x}>\frac{s}{c}$ 时， $g\left(y\right)=0$ 存在大于0的正跟 $y^{*}$ ；再令 $f\left(x\right)=0$ ，有

$x\left(1-x\right)-\sqrt{x}y\left(1+\theta y\right)=0$ , (3.2)

令 $\xi =\sqrt{x}$ ，上式等价于

$h\left(\xi \right)=-{\xi }^3-\frac{c^2\theta }{k^2}{\xi }^2+\frac{2cs\theta -ck+k^2}{k^2}\xi +\frac{ks-s^2\theta }{k^2}=0$ , (3.3)

相应的有

$h^{\prime }\left(\xi \right)=-3{\xi }^2-\frac{2c^2\theta }{k^2}\xi +\frac{2cs\theta -ck+k^2}{k^2}=0$ ,

计算可得

$h\left(0\right)=\frac{ks-s^2\theta }{k^2},h^{\prime }\left(0\right)=\frac{2cs\theta -ck+k^2}{k^2}$ ,

设 $h\left(\xi \right)$ 的三个根分别为 ${\xi }_1,{\xi }_2,{\xi }_3$ ，有 ${\xi }_1{\xi }_2{\xi }_3=\frac{ks-s^2\theta }{k^2}，{\xi }_1+{\xi }_2+{\xi }_3=-\frac{c^2\theta }{k^2}<0$ ，结合笛卡尔符号法则，有：

① $s\theta <k$ ，此时 ${\xi }_1{\xi }_2{\xi }_3>0$ ， $h\left(\xi \right)$ 有一个正根；

② $s\theta =k$ ，此时 $h\left(\xi \right)$ 有一个正根；

③ $s\theta >k$ ，此时 ${\xi }_1,{\xi }_2,{\xi }_3<0$ ， $h\left(\xi \right)$ 有两个正根。

综上， $h\left(\xi \right)$ 至少存在一个正根 ${\xi }^{*}$ ，当 ${\xi }^{*}>\frac{s}{c}$ 时，系统(1.3)存在正平衡点 $E^{*}\left(x^{*},\frac{-s+c\sqrt{x^{*}}}{k}\right)$ 。

引理1 [21] 考虑连续动力系统 $\stackrel{\dot{}}{x}=f\left(x,y,\mu \right)$ ，设 $f\left(x_0,y_0,{\mu }_0\right)=0$ ， $J=Df\left(x_0,y_0,{\mu }_0\right)$ 有一个特征根 $\lambda =0$ ，相应的特征向量为 $v={\left(v_1,v_2\right)}^{\text{T}}$ 以及 $J^{\text{T}}$ 中 $\lambda =0$ 所对应的特征向量为 $w={\left(w_1,w_2\right)}^{\text{T}}$ ，并且其余特征值实部不为0，若满足

$\begin{array}{l}{w}^{\text{T}}{f}_{\mu }\left(x_0,y_0,{\mu }_0\right)=0\\ w^{\text{T}}\left[D{f}_{\mu }\left(x_0,y_0,{\mu }_0\right)v\right]\ne 0\\ w^{\text{T}}\left[D^{2}f\left(x_0,y_0,{\mu }_0\right)\left(v,v\right)\right]\ne 0\end{array}$ ,

则当参数 $\mu$ 穿过分岔值 $\mu ={\mu }_0$ 时， $\stackrel{\dot{}}{x}=f\left(x,y,\mu \right)$ 在 $\left(x_0,y_0\right)$ 附近会经历跨临界分岔。

定理2 当 $s>c$ 时， $E_1\left(1,0\right)$ 为稳定的节点，当 $s<c$ 时， $E_1\left(1,0\right)$ 为鞍点，当 $s=c$ 时，系统在边界平衡点 $E_1\left(1,0\right)$ 处发生跨临界分岔。

证明 在边界平衡点 $E_1\left(1,0\right)$ ，有

$J\left(1,0\right)=\left[\begin{array}{cc}-1& -1\\ 0& -s+c\end{array}\right]$ , (3.4)

显然，当 $s>c$ 时， $E_1\left(1,0\right)$ 为稳定的节点，当 $s<c$ 时， $E_1\left(1,0\right)$ 为鞍点。

当 $s=c$ 时，在 $E_1\left(1,0\right)$ 处有

$J\left(1,0\right)=\left[\begin{array}{cc}-1& -1\\ 0& 0\end{array}\right]$ , (3.5)

因此 $J\left(1,0\right)$ 与 $J\left(1,0\right)$ 都有特征根 $\lambda =0$ ，相对应的特征向量分别为 $v={\left(v_1,v_2\right)}^{\text{T}}={\left(1,-1\right)}^{\text{T}}$ 与 $w={\left(0,a\right)}^{\text{T}}$ ，其中 $a\ne 0$ 。接着，取

$f\left(x,y,s\right)=\left(\begin{array}{c}\frac{x\left(1-x\right)}{1+\theta y}-\sqrt{x}y\\ -sy+c\sqrt{x}y-k{y}^2\end{array}\right)$ , (3.6)

便有

$f_s\left(x,y,s\right)=\left(\begin{array}{c}0\\ -y\end{array}\right)$ , (3.7)

$D^{2}f\left(x_0,y_0,s\right)\left(v,v\right)=\left(\begin{array}{c}\frac{\partial f_1\left(x_0,y_0,s\right)}{\partial x^2}{v}_1{v}_1+\frac{\partial f_1\left(x_0,y_0,s\right)}{\partial x\partial y}{v}_1{v}_2+\frac{\partial f_1\left(x_0,y_0,s\right)}{\partial x\partial y}{v}_1{v}_2+\frac{\partial f_1\left(x_0,y_0,s\right)}{\partial y^2}{v}_2{v}_2\\ \frac{\partial f_2\left(x_0,y_0,s\right)}{\partial x^2}{v}_1{v}_1+\frac{\partial f_2\left(x_0,y_0,s\right)}{\partial x\partial y}{v}_1{v}_2+\frac{\partial f_2\left(x_0,y_0,s\right)}{\partial x\partial y}{v}_1{v}_2+\frac{\partial f_2\left(x_0,y_0,s\right)}{\partial y^2}{v}_2{v}_2\end{array}\right)$ ,

可求得

$w^{\text{T}}{f}_s\left(1,0,c\right)=0$ ,

$w^{\text{T}}\left[D{f}_s\left(1,0,c\right)v\right]=-a\ne 0$ ,

$w^{\text{T}}\left[D^{2}f\left(1,0,c\right)\left(v,v\right)\right]=w^{\text{T}}\left[\begin{array}{c}-2k-1\\ -c\end{array}\right]=-ac\ne 0$ ,

由引理1可得系统在边界平衡点 $E_1\left(1,0\right)$ 处发生跨临界分岔。

定理3 当 $\frac{1}{3}<x^{*}<1$ 时，系统(1.3)的内部平衡点 $E^{*}\left(x^{*},y^{*}\right)$ 稳定。

证明 对于内部平衡点 $E^{*}\left(x^{*},y^{*}\right)$ ，有

$J\left(x^{*},y^{*}\right)=\left[\begin{array}{cc}\frac{1-3x^{*}}{2\left(1+\theta y^{*}\right)}& -\frac{\theta x^{*}\left(1-x^{*}\right)}{{\left(1+\theta y^{*}\right)}^2}-\sqrt{x^{*}}\\ \frac{c{y}^{*}}{2\sqrt{x^{*}}}& -k{y}^{*}\end{array}\right]$ , (3.8)

可以得到

$\{\begin{array}{c}\det J\left(E^{*}\right)=a_{11}{a}_{22}-a_{12}{a}_{21}=-\frac{1-3x^{*}}{2\left(1+\theta y^{*}\right)}k{y}^{*}+\frac{\theta c{y}^{*}\sqrt{x^{*}}\left(1-x^{*}\right)}{2{\left(1+\theta y^{*}\right)}^2}+\frac{c{y}^{*}}{2}\\ trJ\left(E^{*}\right)=a_{11}+a_{22}=\frac{1-3x^{*}-2k{y}^{*}-2k\theta y^{{*}^2}}{2\left(1+\theta y^{*}\right)}k{y}^{*}\end{array}$ , (3.9)

因此，当 $\frac{1}{3}<x^{*}<1$ 时， $\det J\left(E^{*}\right)>0,trJ\left(E^{*}\right)<0$ ，此时， $E^{*}\left(x^{*},y^{*}\right)$ 为稳定的结点或焦点。

定理4 当 $s>\frac{c^2}{4}$ 时，系统在区域 $\left\{x|\frac{1}{2}<x<\sqrt{\frac{s}{c}}\right\}$ 内无闭轨。

证明 计算

$\begin{array}{c}\frac{\partial f}{\partial x}+\frac{\partial g}{\partial y}=\frac{1-2x}{1+\theta y}-\frac{y}{2\sqrt{x}}-s+c\sqrt{x}-2ky\\ =\frac{2\sqrt{x}\left(1-2x\right)-y-\theta y^2-2s\sqrt{x}\left(1+\theta y\right)+2cx\left(1+\theta y\right)-4k\sqrt{x}y\left(1+\theta y\right)}{2\sqrt{x}\left(1+\theta y\right)}\end{array}$ ,

当 $s>\frac{c^2}{4}$ 时， $\frac{\partial f}{\partial x}+\frac{\partial g}{\partial y}$ 在区域 $\left\{x|\frac{1}{2}<x<\sqrt{\frac{s}{c}}\right\}$ 内恒小于零，由Dulac判别法 [20] ，系统(1.3)在区域 $\left\{x|\frac{1}{2}<x<\sqrt{\frac{s}{c}}\right\}$ 内无闭轨。

4. 数值模拟与生态学意义

本小节主要利用Matlab软件对系统进行数值模拟，验证理论分析结果并分析恐惧效应对各种群种群密度的影响。

首先取参数 $s=0.05,c=0.1,k=0.03,\theta =1$ ，利用Matlab计算得系统的内部平衡点为 $E^{*}=\left(0.35,0.30\right)$ ，此时 $x^{*}=0.35>1/3$ ， $s<c$ ，由定理2、定理3可推得内部平衡点 $E^{*}$ 为稳定的焦点，边界平衡点 $E_1\left(1,0\right)$ 为不稳定的鞍点，且系统不存在极限环，其数值模拟的结果如图1所示，其中左侧为相图，右侧为时序图。可以发现此时系统存在一条分界线，从分界线上方出发的点的轨迹最终与y轴正半轴相交，即食饵种群灭绝，从分界线下方出发的点的轨迹会逐渐向内部平衡点靠近，捕食者与食饵种群最终在内部平衡点达到稳态，模拟结果与理论分析相一致。

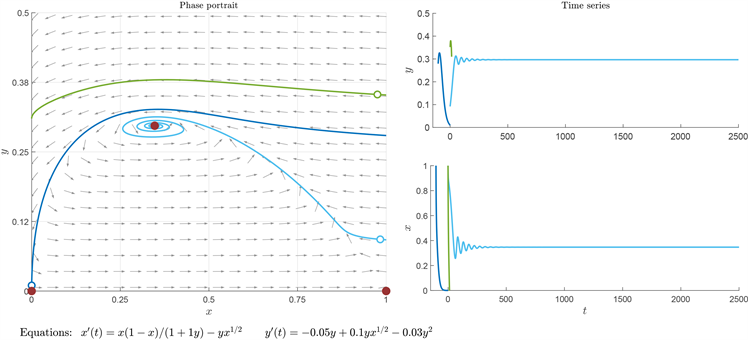
Figure 1. $s=0.05,c=0.1,k=0.03,\theta =1$

图1. $s=0.05,c=0.1,k=0.03,\theta =1$

取参数 $s=0.05,c=0.1,k=0.03,\theta =3$ ，利用Matlab计算得系统的内部平衡点为 $E^{*}=\left(0.32,0.23\right)$ ，数值模拟的结果如图2所示。此时系统的内部平衡点稳定性发生改变， $E^{*}$ 为不稳定的焦点，系统出现一个稳定的极限环，且系统的分界线依然存在，从分界线上方出发的点的轨迹最终与y轴正半轴相交，从分界线下方出发的点的轨迹会逐渐向极限环靠近，捕食者与食饵将以周期震荡的方式共存。

Figure 2. $s=0.05,c=0.1,k=0.03,\theta =3$

图2. $s=0.05,c=0.1,k=0.03,\theta =3$

取参数 $s=0.05,c=0.1,k=0.03,\theta =4.5$ ，利用Matlab计算得系统的内部平衡点为 $E^{*}=\left(0.31,0.20\right)$ ，数值模拟的结果如图3所示，此时内部平衡点 $E^{*}$ 依然为不稳定的焦点，且极限环消失，由任意初始值出发的点的轨迹最终会与y轴正半轴相交，即食饵种群灭绝，在没有食饵种群的情况下，捕食者无法获取能量，由(1.3)，捕食者种群也将随之灭绝。

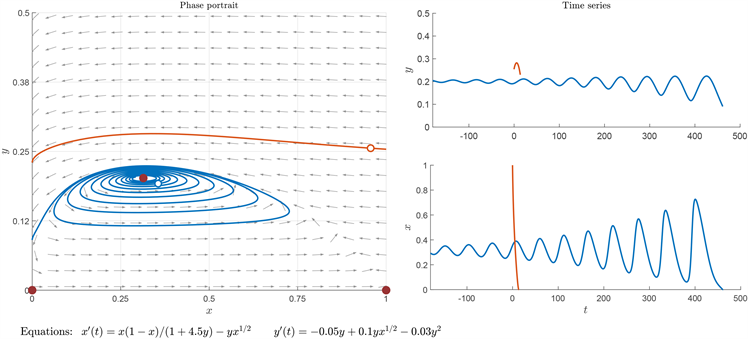
Figure 3. $s=0.05,c=0.1,k=0.03,\theta =4.5$

图3. $s=0.05,c=0.1,k=0.03,\theta =4.5$

在这个过程中，随着参数θ逐渐增大，系统内部平衡点的稳定性由最初的稳定变为不稳定，并在平衡点附近出现一个稳定的极限环，且极限环也随着θ的增大而增大，在该情况下，系统总是存在一条分界曲线，在分界线的上方，捕食者与食饵种群都将灭绝，在分界线下方，两个种群将会在平衡点或极限环处达到稳态；当θ增大到一定程度时，系统的极限环消失，此时无论初始值如何取值，捕食者与食饵种群都会灭绝，即程度过高的恐惧效应将会导致捕食者与食饵种群的灭绝。

5. 结论

本文充分考虑了捕食者对食饵的间接影响，研究了一类具有恐惧效应与群体防御及捕食者种内竞争的捕食者–食饵系统，所提出的系统在生物学上是有效的，因为由第一象限出发的点的轨迹都是非负的和有界的。首先分析了系统在边界平衡点的稳定性，当 $s>c$ 时，边界平衡点稳定，当 $s=c$ 时，在边界平衡点发生跨临界分岔，其次对系统内部平衡点的存在性及稳定性进行分析，并判断了在一定条件下不存在极限环，最后利用Matlab进行数值模拟，发现食饵的恐惧效应会改变系统的轨线性质，当恐惧效应参数过大时，会导致捕食者与食饵种群的灭绝。

基金项目

国家自然科学基金(12161060)。