具有合作捕食与种内竞争的一类捕食者–食饵模型的Hopf分支

Hopf Bifurcation of a Predator-Prey System with Cooperative Hunting and Intraspecific Competition

摘要: 本文研究了一类具有合作捕食和种内竞争的捕食者–食饵模型。该模型的参数空间被划分为几个不同的区域，在每个参数区域，研究了系统的动力学行为，包括内平衡点的个数、稳定性和Hopf分支。结果表明该模型会发生两次Hopf分支。分别与没有合作捕食和不存在种内竞争的捕食者–食饵模型进行比较，指出Hopf分支的发生是由合作捕食引起的，而两次Hopf分支是由种内竞争引起的。

Abstract: We consider a predator-prey model with cooperative hunting and intraspecific competition in predators. The parameter space of the model is divided into several mutually exclusive regions. In each region, the dynamics of the system is investigated, including the number of interior equilibria, stability and Hopf bifurcation. It is presented that Hopf bifurcation may occur twice. By comparing to the dynamics of the systems without cooperative hunting and without the intraspecific competi-tion in predators, respectively, it is shown that the occurrence of Hopf bifurcation is caused by in-traspecific competition.

1. 引言

在生态系统中，捕食者之间的合作捕食是一个很重要的现象 [1] [2] 。近年来，各种捕食者–食饵模型被提出并进行了充分的研究。例如，Cosner等人 [3] 提出了一类捕食者–食饵模型，当捕食者遇到一群食饵时，捕食者会以线性空间的形式觅食并聚集在一起。Berec [4] 研究了一类具有Holling II功能反应与合作捕食的模型，并分析了合作捕食对系统的影响。Pal等人 [5] 考虑了一类Leslie-Gower捕食者–食饵模型，其中捕食者是通过合作进行捕食的，而食饵由于害怕被捕食会表现出反捕食的行为。关于具有合作捕食的常微分方程、反应扩散方程和差分方程的模型还可参考文献 [6] - [12] 。

Alves和Hilker [13] 研究了具有合作捕食的如下捕食者–食饵模型：

$\begin{array}{l}\frac{\text{d}N}{\text{d}t}=rN\left(1-\frac{N}{K}\right)-\left(\lambda +aP\right)NP,\\ \frac{\text{d}P}{\text{d}t}=e\left(\lambda +aP\right)NP-mP.\end{array}$ (1.1)

这里，N和P分别表示食饵和捕食者的种群密度，r和K分别表示食饵种群的内禀增长率和环境容纳量，e是能量转化率，m是捕食者的死亡率， $\lambda$ 是攻击率，a表示捕食者合作捕食的参数。通过数值模拟，研究了系统(1.1)平衡点的稳定性和各种分支行为，包括Hopf分支、同宿分支和Bogdanov-Takens分支。文 [13] 的研究表明，模型(1.1)比熟知的Lotka-Volterra模型具有更复杂的动力学行为，合作捕食可以增强捕食者的攻击率，从而有利于捕食者的生存。然而，文献 [13] 并没有给出一些关键的参数条件，如确定内平衡点确切个数的参数区域和Hopf分支的临界参数值，而主要通过数值模拟描述系统(1.1)动力学行为。Zhang等人 [12] 给出了系统(1.1)内平衡点的确切个数的参数条件，并且讨论了平衡点的局部稳定性和鞍结分支与Hopf分支等动力学行为。基于Alves和Hilker [13] 、Zhang等人 [12] 的研究，本文讨论如下具有合作捕食和种内竞争的捕食者–食饵模型

$\begin{array}{l}\frac{\text{d}x\left(t\right)}{\text{d}t}=x\left(1+\beta x\right)y-dx-e{x}^2,\\ \frac{\text{d}y\left(t\right)}{\text{d}t}=y\left(1-y\right)-\left(1+\beta x\right)xy.\end{array}$ (1.2)

其中，用x和y分别表示捕食者和食饵的种群密度， $e{x}^2$ 表示捕食者的种内竞争，所有参数均为正常数。我们将关于 $\left(\beta ,e\right)$ 的参数空间划分为几个互不相同的区域，并选择d作为分支参数，研究了系统(1.2)在每个的区域的动力学行为，包括内平衡点的数量、稳定性和Hopf分支。结果表明在一定参数区域内，系统会发生两次Hopf分支。

本文的主要内容安排如下：第2节和第3节中，分别研究平衡点的存在性和稳定性；第4节中，我们考虑系统(1.2)的Hopf分支及其方向；第5节中，分别对比捕食者中不存在合作捕食和不存在种内竞争的系统的动态行为，发现系统(1.2)中Hopf分支的发生是由合作捕食引起的，而两次Hopf分支的发生是由捕食种群的种内竞争引起的。

2. 平衡点

在本节，我们讨论系统(1.2)平衡点的个数。系统(1.2)总是存在两个边界平衡点 $E_0\left(0,0\right)$ 和 $E_1\left(0,1\right)$ 。下面我们将讨论内平衡点的存在性。

系统(1.2)的x-零倾斜与y-零倾斜分别为 $y={\varphi }_1\left(x\right):=\frac{d+ex}{1+\beta x}$ 与 $y={\varphi }_2\left(x\right):=-\beta x^2-x+1$ 。显然， $y={\varphi }_1\left(x\right)$ 有水平渐近线 $y=\frac{e}{\beta }$ ；在 $\left[0,+\infty \right)$ 上，当 $d<\frac{e}{\beta }$ 时 $y={\varphi }_1\left(x\right)$ 单调增加，当 $d>\frac{e}{\beta }$ 时 $y={\varphi }_1\left(x\right)$ 单调减小。

$\left(x^{*},y^{*}\right)$ 是系统(1.2)的内平衡点当且仅当 $x^{*}$ 是 ${\varphi }_1\left(x\right)-{\varphi }_2\left(x\right)=0$ 的正根，即 $x^{*}$ 满足 $F\left(x^{*}\right)=d$ 与 $y^{*}={\varphi }_1\left(x^{*}\right)$ ，其中

$F\left(x\right)=-{\beta }^2{x}^3-2\beta x^2+\left(\beta -e-1\right)x+1.$ (2.1)

显然 $F\left(0\right)=1$ ，为此我们只需要讨论函数 $u=F\left(x\right)$ 与 $u=d$ 的正交点。

定义关于 $\left(\beta ,e\right)$ 的双参数空间为

$\Lambda =\left\{\lambda =\left(\beta ,e\right)\in {ℝ}_{+}^2:e\beta >0\right\}.$ (2.2)

我们将 $\Lambda$ 划分为两个区域：

${\Lambda }_1=\left\{\lambda \in \Lambda :e\ge \beta -1\right\}与{\Lambda }_2=\left\{\lambda \in \Lambda :0<e<\beta -1,\beta >1\right\}.$ (2.3)

下面选d作为分支参数分析(1.2)的动力学行为。

如果 $\lambda \in {\Lambda }_1$ ，即 $e\ge \beta -1$ ，那么 $F\left(x\right)$ 在区间 $\left[0,+\infty \right)$ 上单调递减，并且对于任意 $x>0$ ， $F\left(x\right)<F\left(0\right)=1$ 。为此，如果 $d<1$ ，则系统(1.2)存在唯一的一个内平衡点 $E_2^{*}\left(x_2^{*},y_2^{*}\right)$ ；如果 $d\ge 1$ ，则系统(1.2)没有内平衡点(见图1)。

Figure 1. The case of $\lambda \in {\Lambda }_1$ , i.e., $e\ge \beta -1$

图1. $\lambda \in {\Lambda }_1$ 的情形，即 $e\ge \beta -1$

如果 $\lambda \in {\Lambda }_2$ ，即 $0<e<\beta -1,\beta >1$ ，则由 $F^{\prime }\left(x\right)=-3{\beta }^2{x}^2-4\beta x+\beta -e-1$ 可得 $F\left(x\right)$ 的极大值点

$x_0=\frac{-2+\sqrt{1+3\left(\beta -e\right)}}{3\beta }>0.$

当 $x\in \left(0,x_0\right)$ 时， $F\left(x\right)$ 单调递增且 $1<F\left(x\right)<F\left(x_0\right)$ ；当 $x\in \left(x_0,\infty \right)$ 时， $F\left(x\right)$ 单调递减且 $F\left(x\right)<F\left(x_0\right)$ 。因此得到如下结论(参见图2)：

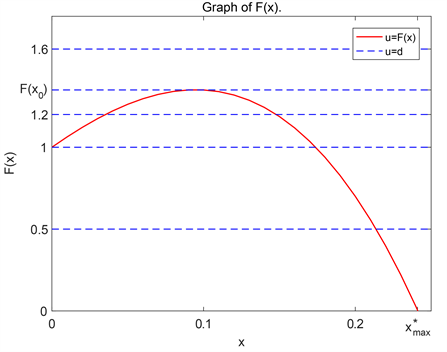
Figure 2. The case of $\lambda \in {\Lambda }_2$ , i.e., $0<e<\beta -1,\beta >1$

图2. $\lambda \in {\Lambda }_2$ 的情形，即 $0<e<\beta -1,\beta >1$

· 若 $d\le 1$ ，则系统(1.2)有唯一的内平衡点 $E_2^{*}\left(x_2^{*},y_2^{*}\right)$ ；

· 若 $1<d<F\left(x_0\right)$ ，则系统(1.2)有两个内平衡点 $E_1^{*}\left(x_1^{*},y_1^{*}\right)$ 和 $E_2^{*}\left(x_2^{*},y_2^{*}\right)$ ，其中 $x_1^{*}<x_0<x_2^{*}$ ；

· 若 $d=F\left(x_0\right)$ ，则 $E_1^{*}$ 和 $E_2^{*}$ 重合，系统(1.2)只存在一个内平衡点 $E^{*}\left(x_0,{\varphi }_1\left(x_0\right)\right)$ ；

· 若 $d>F\left(x_0\right)$ ，则系统(1.2)不存在内平衡点。

综上所述，可得：

定理2.1

1) 如果 $\lambda \in {\Lambda }_1$ ，则当 $d<1$ 时，系统(1.2)存在唯一的内平衡点 $E_2^{*}\left(x_2^{*},y_2^{*}\right)$ ；当 $d\ge 1$ 时，系统(1.2)没有内平衡点(见图1)。

2) 如果 $\lambda \in {\Lambda }_2$ ，则当 $d\le 1$ 时，系统(1.2)存在唯一的内平衡点 $E_2^{*}\left(x_2^{*},y_2^{*}\right)$ ；当 $1<d<F\left(x_0\right)$ 时，系统(1.2)存在两个内平衡点 $E_1^{*}\left(x_1^{*},y_1^{*}\right)$ 和 $E_2^{*}\left(x_2^{*},y_2^{*}\right)$ ，其中 $x_1^{*}<x_0<x_2^{*}$ ；当 $d>F\left(x_0\right)$ 时，系统(1.2)不存在内平衡点；当 $d=F\left(x_0\right)$ 时，系统(1.2)存在唯一的内平衡点 $E^{*}\left(x_0,{\varphi }_1\left(x_0\right)\right)$ (见图2)。

注2.1 由上面的讨论可得：

1) 如果 $d<1$ ，那么系统(1.2)总存在唯一的内平衡点 $E_2^{*}\left(x_2^{*},y_2^{*}\right)$ 。

2) 如果 $E_2^{*}\left(x_2^{*},y_2^{*}\right)$ (或 $E_1^{*}\left(x_1^{*},y_1^{*}\right)$ )存在，则 $F^{\prime }\left(x_2^{*}\right)<0$ (或 $F^{\prime }\left(x_1^{*}\right)>0$ )。

3) 如果 $E_1^{*}\left(x_1^{*},y_1^{*}\right)$ 存在，则 $x_1^{*}$ 随d的增大而增大；如果 $E_2^{*}\left(x_2^{*},y_2^{*}\right)$ 存在，则 $x_2^{*}$ 随d的增大而减小。

4) 如果 $d=\frac{e}{\beta }$ ，则 ${\varphi }_1\left(x\right)=\frac{e}{\beta }$ 。如果 $d=\frac{e}{\beta }<1$ ，则 $x_2^{*}=x_{\max }^{*}$ ，其中 $x_{\max }^{*}=\frac{-1+\sqrt{1+4\left(\beta -e\right)}}{2\beta }$ 。

因此，如果 $d>\frac{e}{\beta }$ 和 $E_2^{*}\left(x_2^{*},y_2^{*}\right)$ 存在，并且由 $x_2^{*}$ 关于d的单调性可知 $x_0<x_2^{*}<x_{\max }^{*}$ 。

5) 如果 $d\le \frac{e}{\beta }$ 且 $E_2^{*}\left(x_2^{*},y_2^{*}\right)$ 存在，则 $y_2^{*}={\varphi }_2\left(x_2^{*}\right)\ge d$ 。

6) $F\left(x_0\right)=\frac{2{\left(1+3\left(\beta -e\right)\right)}^{\frac{3}{2}}+9\left(\beta +2e\right)+2}{27\beta }$ 。

3. 平衡点的稳定性

在本节，我们研究系统(1.2)平衡点的稳定性。系统(1.2)的雅可比矩阵为

$J=\left(\begin{array}{cc}\left(1+2\beta x\right)y-d-2ex& \left(1+\beta x\right)x\\ -\left(1+2\beta x\right)y& 1-2y-\left(1+\beta x\right)x\end{array}\right).$ (3.1)

3.1. 边界平衡点的稳定

首先分析系统(1.2)边界平衡点 $E_0\left(0,0\right)$ 和 $E_1\left(0,1\right)$ 的局部稳定性。

1) $E_0\left(0,0\right)$ 是鞍点。

2) 如果 $d>1$ 或 $d=1$ 且 $e=\beta -1$ ， $E_1\left(0,1\right)$ 是稳定的结点；如果 $d<1$ ， $E_1\left(0,1\right)$ 是鞍点；如果 $d=1$ 且 $e\ne \beta -1$ ， $E_1\left(0,1\right)$ 是一个鞍结点。

证明 根据雅可比矩阵(3.1)，显然 $E_0$ 是鞍点。

当 $d\ne 1$ 时， $E_1$ 的稳定性显然。现在我们证明 $d=1$ 的情形， $E_1$ 处的雅可比矩阵的特征值分别为 ${\kappa }_1=0$ 、 ${\kappa }_2=-1$ ，从而得到 $E_1$ 是一个非双曲平衡点，下面利用中心流形定理 [14] 来确定 $E_1$ 的类型。

令 $x=X$ ， $y=Y+1$ 进行变换，然后令 $X=u$ ， $Y=v-u$ ，则系统(1.2)转化为

$\begin{array}{l}\frac{\text{d}u\left(t\right)}{\text{d}t}=\left(\beta -e-1\right)u^2+uv+\beta u^{2}v-\beta u^3,\\ \frac{\text{d}v\left(t\right)}{\text{d}t}=-v-\left(e+1\right)u^2+2uv-v^2.\end{array}$ (3.2)

容易得到中心流形上的解所满足的方程为 $\frac{\text{d}u}{\text{d}v}=\left(\beta -e-e\right)u^2-\left(\beta +e+1\right)u^3+o\left(u^3\right)$ 。从而根据中心流

形定理 [14] ，可知当 $e\ne \beta -1$ 时， $E_1$ 是鞍结点；当 $e=\beta -1$ 时，它是稳定的结点。

3.2. 内平衡点的稳定性

下面考虑系统(1.2)内平衡点的局部稳定性。内平衡点 $E^{*}\left(x^{*},y^{*}\right)$ 处的雅可比矩阵(3.1)为

${J|}_{E^{*}}=\left(\begin{array}{cc}\left(\beta y^{*}-e\right)x^{*}& \left(1+\beta x^{*}\right)x^{*}\\ -\left(1+\beta x^{*}\right)y^{*}-\beta x^{*}{y}^{*}& -y^{*}\end{array}\right).$ (3.3)

其对应的特征方程为

${\kappa }^2-{\omega }_1\kappa +{\omega }_2=0,$ (3.4)

其中 ${\omega }_1={TrJ|}_{E^{*}}$ ， ${\omega }_2={DetJ|}_{E^{*}}$ 。由于 $y^{*}={\varphi }_1\left(x^{*}\right)=\frac{d+e{x}^{*}}{1+\beta x^{*}}$ ，即 $x^{*}\left(\beta y^{*}-e\right)=d-y^{*}$ ，

$y^{*}={\varphi }_2\left(x^{*}\right)=-\beta {\left(x^{*}\right)}^2-x^{*}+1$ 且 $d=F\left(x^{*}\right)$ ， ${\omega }_1$ 可表示为

${\omega }_1=d-2y^{*}=-{\beta }^2{\left(x^{*}\right)}^3+\left(\beta +1-e\right)x^{*}-1,$ (3.5)

${\omega }_2$ 可表示为

${\omega }_2=-x^{*}{y}^{*}{F}^{\prime }\left(y^{*}\right).$ (3.6)

由注2.1，如果 $E_1^{*}\left(x_1^{*},y_1^{*}\right)$ 存在，则 $F^{\prime }\left(x_1^{*}\right)>0$ ，故 $E_1^{*}$ 是鞍点；如果 $E_2^{*}\left(x_2^{*},y_2^{*}\right)$ 存在，则 $F^{\prime }\left(x_2^{*}\right)<0$ ，因此 $E_2^{*}$ 的稳定性由 ${\omega }_1={TrJ|}_{E_2^{*}}$ 的符号决定。为此，我们定义

$\psi \left(x\right)=-{\beta }^2{x}^3+\left(\beta +1-e\right)x-1.$ (3.7)

引理3.2 如果 $\psi \left(x_2^{*}\right)<0$ ，则 $E_2^{*}\left(x_2^{*},y_2^{*}\right)$ 是汇；如果 $\psi \left(x_2^{*}\right)>0$ ，则其是源。

引理3.2并没有给出 $E_2^{*}\left(x_2^{*},y_2^{*}\right)$ 是稳定或不稳定的显式参数区域。为此，我们需要进一步讨论 $\psi \left(x\right)$ 的性质。

显然， $\psi \left(x\right)$ 具有如下性质：

· 如果 $e\ge \beta +1$ ，则对于所有 $x\ge 0$ ，都有 $\psi \left(x\right)<0$ 。

· 如果 $e<\beta +1$ ，则 $\psi \left(x\right)$ 存在一个正的极大值点

$\tilde{x}=\frac{\sqrt{\beta +1-e}}{\sqrt{3}\beta }$ (3.8)

且

$\psi \left(\tilde{x}\right)=\frac{2}{\sqrt{27}\beta }{\left(\beta -e+1\right)}^{\frac{3}{2}}-1.$ (3.9)

故当 $x\in \left(0,\tilde{x}\right)$ 时， $\psi \left(x\right)$ 单调递增；当 $x>\tilde{x}$ 时 $\psi \left(x\right)$ 单调递减。

· 如果 $\psi \left(\tilde{x}\right)>0$ ， $\psi \left(x\right)$ 有两个正根 ${\xi }_1$ 和 ${\xi }_2$ ( $0<{\xi }_1<{\xi }_2$ )。当 $0<x<{\xi }_1$ 或 $x>{\xi }_2$ 时， $\psi \left(x\right)<0$ ；当 ${\xi }_1<x<{\xi }_2$ 时， $\psi \left(x\right)>0$ 。 ${\xi }_1$ 和 ${\xi }_2$ 确切表达式可以表示如下：

$\begin{array}{l}{\xi }_1=2\tilde{x}\sin \left(\frac{\pi }{6}-\frac{{\theta }_0}{3}\right),{\xi }_2=2\tilde{x}\sin \left(\frac{\pi }{6}+\frac{{\theta }_0}{3}\right),\\ {\theta }_0=\arccos \frac{1}{\psi \left(\tilde{x}\right)+1},0<{\theta }_0<\frac{\pi }{2}.\end{array}$ (3.10)

由引理3.2，我们得到以下结果：

引理3.3

1) 如果 $e\ge \beta +1$ 或 $e<\beta +1$ ， $\psi \left(\tilde{x}\right)<0$ ，则 $E_2^{*}\left(x_2^{*},y_2^{*}\right)$ (若存在)是汇。

2) 如果 $e<\beta +1$ ， $\psi \left(\tilde{x}\right)>0$ ， $E_2^{*}\left(x_2^{*},y_2^{*}\right)$ 存在，则当 $x_2^{*}\in \left(0,{\xi }_1\right)$ 或 $x_2^{*}\in \left({\xi }_2,\infty \right)$ ， $E_2^{*}\left(x_2^{*},y_2^{*}\right)$ 是汇；当 $x_2^{*}\in \left({\xi }_1,{\xi }_2\right)$ ， $E_2^{*}$ 是源。

引理3.3表明，确定 $\psi \left(\tilde{x}\right)$ 的符号对 $E_2^{*}$ 的稳定性是十分重要的。注意到当 $d>\frac{e}{\beta }$ 时 $x_0<x_2^{*}<x_{\max }^{*}$ (见注2.1)，我们需要考虑 $\psi \left(x_{\max }^{*}\right)$ 、 ${\psi }^{\prime }\left(x_{\max }^{*}\right)$ 、 $\psi \left(x_0\right)$ 和 ${\psi }^{\prime }\left(x_0\right)$ 的符号。

定义

$f_1\left(\beta \right)=\beta +1-3{\left(\frac{\beta }{2}\right)}^{\frac{2}{3}}.$ (3.11)

显然， $f_1\left(2\right)=0$ 和 ${f^{\prime }}_1\left(\beta \right)=1-{\left(\frac{\beta }{2}\right)}^{-\frac{1}{3}}$ 。因此，当 $0<\beta <2$ 时， $f_1\left(\beta \right)$ 单调递减；当 $\beta >2$ 时， $f_1\left(\beta \right)$ 单

调增加且 $\beta -2>f_1\left(\beta \right)$ 。由(3.9)，可之路 $\psi \left(\tilde{x}\right)<0$ 当且仅当 $e>f_1\left(\beta \right)$ 。

当 $e<\beta$ 时， $\psi \left(x_{\max }^{*}\right)=-\frac{e}{\beta }<0$ 且 ${\psi }^{\prime }\left(x_{\max }^{*}\right)=-\frac{4\left(\beta -e\right)+1}{2}+\frac{3\sqrt{1+4\left(\beta -e\right)}}{2}$ ，进而得到

${\psi }^{\prime }\left(x_{\max }^{*}\right)>0\iff \left(\beta -e-2\right)\left(4\left(\beta -e\right)+1\right)<0\iff e>\beta -2$ 。

当 $e<\beta -1$ 且 $\beta >1$ 时，可得 ${\psi }^{\prime }\left(x_0\right)=\frac{1}{3}\left(-2+4\sqrt{1+3\left(\beta -e\right)}\right)$ 且

$\psi \left(x_0\right)=\frac{2\left(3\left(\beta -e\right)-2\right)\sqrt{1+3\left(\beta -e\right)}-27\beta -4}{9\beta }$ ，显然 ${\psi }^{\prime }\left(x_0\right)>0$ 。

定义

$\mathcal{M}\left(\beta ,e\right)=2\left(3\left(\beta -e\right)-2\right)\sqrt{1+3\left(\beta -e\right)}-27\beta -4,$

显然， $\mathcal{M}\left(8,0\right)=0$ 且

$\begin{array}{l}\frac{\partial \mathcal{M}}{\partial \beta }=6\sqrt{3\left(\beta -e\right)+1}+\frac{3\left(3\left(\beta -e\right)-2\right)}{\sqrt{3\left(\beta -e\right)+1}}-27>0,\\ \frac{\partial \mathcal{M}}{\partial e}=-6\sqrt{3\left(\beta -e\right)+1}-\frac{3\left(3\left(\beta -e\right)-2\right)}{\sqrt{3\left(\beta -e\right)+1}}<0.\end{array}$

由隐函数定理，方程 $\mathcal{M}\left(\beta ,e\right)=0$ 确定了一个函数 $e=f_2\left(\beta \right)$ ，函数 $f_2\left(\beta \right)$ 在 $\beta >2$ 时是递增的，其中

$\beta -\frac{1}{3}{\left(1+\frac{a\left(\beta \right)}{2}+\sqrt{\left(1+\frac{a{\left(\beta \right)}^2}{2}\right)-1}\right)}^{\frac{1}{3}}-\frac{1}{3}{\left(1+\frac{a\left(\beta \right)}{2}-\sqrt{\left(1+\frac{a{\left(\beta \right)}^2}{2}\right)-1}\right)}^{\frac{1}{3}}-\frac{1}{3},$ (3.12)

这里 $a\left(\beta \right)=\frac{27\beta }{4}\left(27\beta +8\right)$ 。因此，当 $2<\beta <8$ 时， $f_2\left(\beta \right)<0$ ；当 $\beta >8$ 时， $f_2\left(\beta \right)>0$ 。所以，当且仅当 $e<f_2\left(\beta \right)$ ( $\beta >8$ )时， $\psi \left(x_0\right)>0$ 。此外，由 $a\left(\beta \right)>{\left(\frac{27\beta }{4}\right)}^2$ ，可知

$f_2\left(\beta \right)<\beta -\frac{1}{3}{\left(a\left(\beta \right)\right)}^{\frac{1}{3}}<\beta +1-3{\left(\frac{\beta }{2}\right)}^{\frac{2}{3}}=f_1\left(\beta \right)\left(\beta >2\right).$

最后，我们证明当 $e=f_1\left(\beta \right)$ ( $\beta >2$ )时，有 $x_0<\tilde{x}$ 。事实上，如果 $e=f_1\left(\beta \right)$ ，由方程(3.8)可知

$\tilde{x}=\frac{{\left(\frac{\beta }{2}\right)}^{\frac{1}{3}}}{\beta }$

以及由方程(2.4)可知

$x_0=\frac{-2+\sqrt{{\left(\frac{27\beta }{2}\right)}^{\frac{2}{3}}-2}}{3\beta }>0.$

显然， $x_0<\tilde{x}$ 。

综上所述，我们有以下结论：

引理3.4

1) 若 $f_1\left(\beta \right)<e<\beta +1$ ，则 $\psi \left(\tilde{x}\right)<0$ 。

2) 若 $e=f_1\left(\beta \right)$ 且 $\beta >2$ ，则 $\psi \left(\tilde{x}\right)=0$ 且 $x_0<\tilde{x}$ 。

3) 若 $e<\beta$ ，则 $\psi \left(x_{\max }^{*}\right)=-\frac{e}{\beta }<0$ ，当且仅当 $e>\beta -2$ 时， ${\psi }^{\prime }\left(x_{\max }^{*}\right)>0$ 。

4) 若 $e<\beta -1$ ， $\beta >1$ ，则 ${\psi }^{\prime }\left(x_0\right)>0$ ，当且仅当 $e<f_2\left(\beta \right)$ ， $\beta >8$ 时， $\psi \left(x_0\right)>0$ 。

5) 对于任意的 $\beta >2$ ，都有 $f_2\left(\beta \right)<f_1\left(\beta \right)<\beta -2$ 。

注如果 ${\psi }^{\prime }\left(x_0\right)>0$ 且 $\psi \left(x_0\right)=0$ ，则 $x_0={\xi }_1$ 。

基于引理3.4，我们可将区域 ${\Lambda }_2$ 划分为以下两个子区域(见图3)：

$\begin{array}{l}{\Lambda }_{2a}=\left\{\lambda \in {\Lambda }_2:\beta >1,\beta -2\le e<\beta -1\right\}\cup \left\{\lambda \in {\Lambda }_2:\beta >2,f_1\left(\beta \right)\le e<\beta -2\right\},\\ {\Lambda }_{2b}=\left\{\lambda \in {\Lambda }_2:0<e<f_1\left(\beta \right),\beta >2\right\}.\end{array}$ (3.13)

进一步，将 ${\Lambda }_{2b}$ 划分为两个区域(见图3)：

$\begin{array}{l}{\Lambda }_{2b-1}=\left\{\lambda \in {\Lambda }_{2b}:f_2\left(\beta \right)<e<f_1\left(\beta \right),\beta >2\right\},\\ {\Lambda }_{2b-2}=\left\{\lambda \in {\Lambda }_{2b}:e\le f_2\left(\beta \right),\beta >8\right\}.\end{array}$

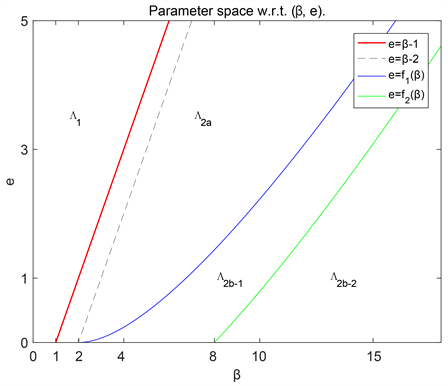
Figure 3. The parameter space of $\left(\beta ,e\right)$ . $\Lambda ={\Lambda }_1\cup {\Lambda }_2$ , where ${\Lambda }_2={\Lambda }_{2a}\cup {\Lambda }_{2b}$ , ${\Lambda }_{2b}={\Lambda }_{2b-1}\cup {\Lambda }_{2b-2}$

图3. $\left(\beta ,e\right)$ 的参数空间， $\Lambda ={\Lambda }_1\cup {\Lambda }_2$ ，其中 ${\Lambda }_2={\Lambda }_{2a}\cup {\Lambda }_{2b}$ ， ${\Lambda }_{2b}={\Lambda }_{2b-1}\cup {\Lambda }_{2b-2}$

下面我们讨论以下三种情况内平衡点 $E_2^{*}\left(x_2^{*},y_2^{*}\right)$ 的稳定性：1) $\lambda \in {\Lambda }_1$ ，2) $\lambda \in {\Lambda }_{2a}$ ，3) $\lambda \in {\Lambda }_{2b}={\Lambda }_{2b-1}\cup {\Lambda }_{2b-2}$ 。

1) 若 $\lambda \in {\Lambda }_1$ (即 $e\ge \beta -1$ )，由定理2.1可知，则当 $d<1$ 时系统(1.2)存在唯一的内平衡点 $E_2^{*}\left(x_2^{*},y_2^{*}\right)$ 。我们考虑以下两种情况：i) $e\ge \beta$ ，ii) $\beta -1<e<\beta$ 。

i) 设 $e\ge \beta$ (即 $\frac{e}{\beta }\ge 1$ )，则对于任意的 $d<1$ ，都有 $y_2^{*}>d$ (见注2.1和图2)，因此 ${\omega }_1=d-2y^{*}<0$ ，

故 $E_2^{*}$ 是局部渐近稳定的。

ii) 设 $\beta -1<e<\beta$ ，则存在 $\frac{e}{\beta }<1$ 和(3.8)中所给的 $\tilde{x}$ 。

a) 如果 $d\le \frac{e}{\beta }$ ，类似于情形i)，则 $E_2^{*}$ 是局部渐近稳定的。

b) 如果 $\frac{e}{\beta }<d<1$ ，则 $0<x_2^{*}<x_{\max }^{*}$ (见注2.1)。根据引理3.4， $\psi \left(x_{\max }^{*}\right)<0$ 且 ${\psi }^{\prime }\left(x_{\max }^{*}\right)>0$ 。由函数 $\psi (\; x\; )$

的性质可知， $x_{\max }^{*}<\tilde{x}$ ，因此 $\psi \left(x_2^{*}\right)<\psi \left(x_{\max }^{*}\right)<0$ 。由引理3.2，得出 $E_2^{*}$ 是局部渐近稳定的。

因此，在 $\lambda \in {\text{Λ}}_1$ 的情况下， $E_2^{*}$ (若存在)是局部渐近稳定的。

2) 若 $\lambda \in {\Lambda }_{2a}$ ，由定理2.1，则当 $d\le 1$ 时系统(1.2)存在唯一的内平衡点 $E_2^{*}$ ；当 $1<d<F\left(x_0\right)$ 时存在两个内平衡 $E_1^{*}$ 和 $E_2^{*}$ 。我们考虑以下两种情况：i) $\beta -2<e<\beta -1$ ， $\beta >1$ ；ii) $f_1\left(\beta \right)\le e\le \beta -2$ ， $\beta >2$ 。

首先，如果 $d\le \frac{e}{\beta }$ ，则类似于前面1)，对于每种情况， $E_2^{*}$ 是局部渐近稳定的。因此，下面我们假设 $\frac{e}{\beta }<d<F\left(x_0\right)$ 。

i) 设 $\beta -2<e<\beta -1$ ， $\beta >1$ ，则 $x_0<x_2^{*}<x_{\max }^{*}$ (见注2.1)。由引理3.4可知， $\psi \left(x_{\max }^{*}\right)<0$ 且 ${\psi }^{\prime }\left(x_{\max }^{*}\right)>0$ ，这意味着 $x_{\max }^{*}<\tilde{x}$ ，结合 $\psi \left(x\right)$ 在 $\left(0,\tilde{x}\right)$ 上单调性， $\psi \left(x_2^{*}\right)<\psi \left(x_{\max }^{*}\right)<0$ 。因此，由引理3.2可知， $E_2^{*}$ 是局

部渐近稳定的。当 $e=\beta -2$ ，有 $\tilde{x}=\frac{1}{e+2}$ 和 $\psi \left(\tilde{x}\right)=\frac{2}{e+2}-1<0$ ， $E_2^{*}$ ，则由引理3.3可知， $E_2^{*}$ 是局部渐近

稳定的。

ii) 设 $f_1\left(\beta \right)\le e\le \beta -2$ ( $\beta >2$ )，则由引理3.4可知， $\psi \left(\tilde{x}\right)<0$ ，因此，根据引理3.3可知， $E_2^{*}$ 是局部渐近稳定的。如果 $e=f_1\left(\beta \right)$ ，那么由引理3.4， $\psi \left(x\right)=0$ 存在唯一的正根 $\tilde{x}$ ( $x_0<\tilde{x}$ )且 $\psi \left(\tilde{x}\right)=0$ 。由引理3.4可知， $\psi \left(x_{\max }^{*}\right)<0$ 且 ${\psi }^{\prime }\left(x_{\max }^{*}\right)<0$ ，这意味着根据函数 $\psi \left(x\right)$ 的性质，有 $x_{\max }^{*}>\tilde{x}$ 。因为 $x_2^{*}$ 随着

$d\in \left(\frac{e}{\beta },F\left(x_0\right)\right)$ 的增加而减少， ${x_2^{*}|}_{d=\frac{e}{\beta }}=x_{\max }^{*}$ 且 ${x_2^{*}|}_{d=F\left(x_0\right)}=x_0$ ，所以存在 $\tilde{d}$ ( $\tilde{d}\in \left(\frac{e}{\beta },F\left(x_0\right)\right)$ )，使得当 $d=\tilde{d}$ 时， $x_2^{*}=\tilde{x}$ ；当 $d\in \left(\frac{e}{\beta },\tilde{d}\right)$ 时， $x_2^{*}\in \left(\tilde{x},x_{\max }^{*}\right)$ ；当 $d\in \left(\tilde{d},F\left(x_0\right)\right)$ 时， $x_2^{*}\in \left(x_0,\tilde{x}\right)$ 。因此，由 $\psi \left(x\right)$ 的性质和

引理3.3可知，当 $d\ne \tilde{d}$ 时， $\psi \left(x_2^{*}\right)<0$ ，故 $E_2^{*}$ 是局部渐近稳定的。这意味着在 $d=\tilde{d}$ 附近(3.4)的特征值不

能通过虚轴，则对于任意的 $d\in \left(\frac{e}{\beta },F\left(x_0\right)\right)$ ， $E_2^{*}$ 是局部渐近稳定的。

因此，在 $\lambda \in {\Lambda }_{2a}$ 的情况下， $E_2^{*}$ (若存在)是局部渐近稳定的。

3) 若 $\lambda \in {\Lambda }_{2b}$ (即 $e<f_1\left(\beta \right)$ ， $\beta >2$ )，由定理2.1，则当 $d\le 1$ 时系统(1.2)存在唯一的内平衡点 $E_2^{*}$ ；当 $1<d<F\left(x_0\right)$ 时存在两个内平衡点 $E_1^{*}$ 和 $E_2^{*}$ 。由引理3.4， $\psi \left(x\right)=0$ 有两个正根 ${\xi }_1$ 和 ${\xi }_2$ ( $0<{\xi }_1<{\xi }_2$ )。

i) 设 $d\le \frac{e}{\beta }$ ，则类似于情形(1)， $E_2^{*}$ 是局部渐近稳定的。

ii) 设 $\frac{e}{\beta }<d<F\left(x_0\right)$ ，则 $x_0<x_2^{*}<x_{\max }^{*}$ (见备注2.1)。由引理3.4可知， $\psi \left(x_{\max }^{*}\right)<0$ 和 ${\psi }^{\prime }\left(x_{\max }^{*}\right)<0$ ，

这意味着 $x_{\max }^{*}>{\xi }_2$ 。

a) 如果 $\lambda \in {\Lambda }_{2b-1}$ (即 $f_2\left(\beta \right)<e<f_1\left(\beta \right)$ )，由引理3.4， $\psi \left(x_0\right)>0$ 、 ${\psi }^{\prime }\left(x_0\right)>0$ ，因此 $x_0<{\xi }_1$ 。所以

$x_0<{\xi }_1<{\xi }_2<x_{\max }^{*}$ 。由于 $x_2^{*}$ 随着 $d\in \left(\frac{e}{\beta },F\left(x_0\right)\right)$ 的增大而减少，并且 ${x_2^{*}|}_{d=\frac{e}{\beta }}=x_{\max }^{*}$ ， ${x_2^{*}|}_{d=F\left(x_0\right)}=x_0$ ，因此存在 $d_1^{*}$ 和 $d_2^{*}$ 满足 $\frac{e}{\beta }<d_1^{*}<d_2^{*}<F\left(x_0\right)$ ，使得当 $d=d_1^{*}$ 时， $x_2^{*}={\xi }_2$ ；当 $d=d_2^{*}$ 时， $x_2^{*}={\xi }_1$ 。并且i) 若 $d\in \left(\frac{e}{\beta },d_1^{*}\right)$ ， $x_2^{*}\in \left({\xi }_2,x_{\max }^{*}\right)$ ；ii) 若 $d\in \left(d_1^{*},d_2^{*}\right)$ ， $x_2^{*}\in \left({\xi }_1,{\xi }_2\right)$ ；iii) 若 $d\in \left(d_2^{*},F\left(x_0\right)\right)$ ， $x_2^{*}\in \left(x_0,{\xi }_1\right)$ 。则由 $\psi \left(x\right)$ 的性质

和引理3.3，我们可以得到以下结论：

i) 若 $d\in \left(\frac{e}{\beta },d_1^{*}\right)$ ， $\psi \left(x_2^{*}\right)<0$ ，则 $E_2^{*}$ 是局部渐近稳定的；ii) 若 $d\in \left(d_1^{*},d_2^{*}\right)$ ， $\psi \left(x_2^{*}\right)>0$ 则 $E_2^{*}$ 是不

稳定的焦点或结点；(iii) 若 $d\in \left(d_2^{*},F\left(x_0\right)\right)$ ， $\psi \left(x_2^{*}\right)<0$ ，则 $E_2^{*}$ 是局部渐近稳定的。

b) 如果 $\lambda \in {\Lambda }_{2b-2}$ (即 $e\le f_2\left(\beta \right)$ ， $\beta >8$ )，则由引理3.4， $\psi \left(x_0\right)\ge 0$ ， ${\psi }^{\prime }\left(x_0\right)>0$ ，因此 ${\xi }_1\ge x_0$ ，所

以 ${\xi }_1\le x_0<{\xi }_2<x_{\max }^{*}$ 。类似上述讨论，存在 $d^{*}$ 满足 $\frac{e}{\beta }<d^{*}<F\left(x_0\right)$ ，使得i) 若 $d\in \left(\frac{e}{\beta },d^{*}\right)$ ， $\psi \left(x_2^{*}\right)<0$ ，

则 $E_2^{*}$ 是局部渐近稳定的；ii) 若 $d\in \left(d^{*},F\left(x_0\right)\right)$ ， $\psi \left(x_2^{*}\right)>0$ ，则 $E_2^{*}$ 是不稳定的焦点或结点。

综上所述，关于内平衡点的局部稳定性，我们得到了如下结论：

定理3.5

1. 如果 $E_1^{*}\left(x_1^{*},y_1^{*}\right)$ 存在，则 $E_1^{*}$ 是一个鞍点。

2. 对于 $E_2^{*}\left(x_2^{*},y_2^{*}\right)$ ，我们有以下情形：

1) 如果 $\lambda \in {\Lambda }_1\cup {\Lambda }_{2a}$ ，则 $E_2^{*}$ (若存在)是局部渐近稳定的。

2) 如果 $\lambda \in {\Lambda }_{2b-1}$ ，则i) 当 $d\le \frac{e}{\beta }$ 时， $E_2^{*}$ 是局部渐近稳定的；ii) 当 $\frac{e}{\beta }<d<F\left(x_0\right)$ 时，存在 $d_1^{*}$ 和 $d_2^{*}$ 满足 $\frac{e}{\beta }<d_1^{*}<d_2^{*}<F\left(x_0\right)$ ，使得当 $d\in \left(\frac{e}{\beta },d_1^{*}\right)$ 或 $d\in \left(d_2^{*},F\left(x_0\right)\right)$ 时， $E_2^{*}$ 是局部渐近稳定的；当 $d\in \left(d_1^{*},d_2^{*}\right)$ 时， $E_2^{*}$ 是不稳定的。

3) 如果 $\lambda \in {\Lambda }_{2b-2}$ ，则i) 当 $d\le \frac{e}{\beta }$ 时， $E_2^{*}$ 是局部渐近稳定的；ii) 当 $\frac{e}{\beta }<d<F\left(x_0\right)$ 时，存在 $d^{*}$ 满足 $\frac{e}{\beta }<d^{*}<F\left(x_0\right)$ ，使得当 $d\in \left(\frac{e}{\beta },d^{*}\right)$ 时， $E_2^{*}$ 是局部渐近稳定的；当 $d\in \left(d^{*},F\left(x_0\right)\right)$ 时， $E_2^{*}$ 是不稳定的。

4. Hopf分支

定理3.5表明，当 $\lambda \in {\Lambda }_{2b-1}$ ，即 $f_2\left(\beta \right)<e<f_1\left(\beta \right)$ 时，系统(1.2)在 $E_2^{*}$ 处可能发生两次Hopf分支；当

$\lambda \in {\Lambda }_{2b-2}$ ，即 $e<f_2\left(\beta \right)$ 时，系统(1.2)在 $E_2^{*}$ 处可能发生一次Hopf分支。下面我们研究系统(1.2)的Hopf分支及其方向。

定理4.1

1) 设 $\lambda \in {\Lambda }_{2b-1}$ ，即 $f_2\left(\beta \right)<e<f_1\left(\beta \right)$ 且 $\beta >2$ ，则当d在 $d\in \left(\frac{e}{\beta },F\left(x_0\right)\right)$ 上增大时，系统(1.2)在 $E_2^{*}$ 处

发生两次Hopf分支：当 $d=d_1^{*}$ 时系统(1.2)发生超临界向前的Hopf分支；当 $d=d_2^{*}$ 时发生超临界向后的Hopf分支。

2) 设 $\lambda \in {\Lambda }_{2b-2}$ ，即 $e<f_2\left(\beta \right)$ 且 $\beta >8$ ，则当 $d=d^{*}$ 时，系统(1.2)在 $E_2^{*}$ 处发生超临界向前的Hopf分支。

证明：若 $\lambda =\left(e,\beta \right)\in {\Lambda }_{2b-1}$ ，根据定理3.5，则存在 $d_1^{*},d_2^{*}$ 满足 $\frac{e}{\beta }<d_1^{*}<d_2^{*}<F\left(y_0\right)$ ，使得当 $d\in \left(\frac{e}{\beta },d_1^{*}\right)$ 或 $d\in \left(d_2^{*},F\left(y_0\right)\right)$ 时， $E_2^{*}$ 是局部渐近稳定的；当 $d\in \left(d_1^{*},d_2^{*}\right)$ 时， $E_2^{*}$ 是不稳定的。若 $\lambda =\left(e,\beta \right)\in {\Lambda }_{2b-2}$ ，则存在 $d^{*}$ 满足 $\frac{e}{\beta }<d^{*}<F\left(y_0\right)$ ，使得当 $d\in \left(\frac{e}{\beta },d^{*}\right)$ 时， $E_2^{*}$ 是局部渐近稳定的；当 $d\in \left(d^{*},F\left(y_0\right)\right)$ 时， $E_2^{*}$ 是不稳定的。

在 $d=\bar{d}$ 处(当 $\lambda \in {\Lambda }_{2b-1}$ 时， $\bar{d}=d_1^{*},d_2^{*}$ ；当 $\lambda \in {\Lambda }_{2b-2}$ 时， $\bar{d}=d^{*}$ )， ${\omega }_1=\psi \left(x_2^{*}\right)=0$ ， $E_2^{*}$ 处的特征方程

(3.4)有一对纯虚根 $\kappa =\pm \sqrt{{\omega }_2}$ 。当d接近 $\bar{d}$ 时，设 $\kappa ={\varrho }_1\left(d\right)\pm i\sqrt{{\varrho }_2\left(d\right)}$ 为方程(3.4)的根，则 ${\varrho }_1\left(d\right)=\frac{1}{2}{\omega }_1=\frac{1}{2}\psi \left(x_2^{*}\right)$ ， ${\varrho }_2\left(d\right)=\frac{1}{2}\left({\omega }_1^2-4{\omega }_2\right)$ 。显然， $\frac{\partial {\varrho }_1\left(d\right)}{\partial d}=\frac{1}{2}{\psi }^{\prime }\left(x_2^{*}\right)\frac{\partial x_2^{*}}{\partial d}$ 。

若 $\lambda =\left(e,\beta \right)\in {\Lambda }_{2b-1}$ ，则当 $d=d_1^{*}$ 时， ${\psi }^{\prime }\left(x_2^{*}\right)={\psi }^{\prime }\left({\xi }_2\right)<0$ ；当 $d=d_2^{*}$ 时， ${\psi }^{\prime }\left(x_2^{*}\right)={\psi }^{\prime }\left({\xi }_1\right)>0$ 。注意到

$\frac{\partial x_2^{*}}{\partial d}<0$ (见备注2.1)，当 $d=d_1^{*}$ 时， $\frac{\partial {\varrho }_1\left(d\right)}{\partial d}>0$ ；当 $d=d_2^{*}$ 时， $\frac{\partial {\varrho }_1\left(d\right)}{\partial d}<0$ 。类似地，如果 $\lambda =\left(e,\beta \right)\in {\Lambda }_{2b-2}$ ，则当 $d=d^{*}$ 时， $\frac{\partial {\varrho }_1\left(d\right)}{\partial d}>0$ 。因此，由Poincaré-Hopf分支定理 [15] 可知，当 $d=\bar{d}$ 时，系统(1.2)在 $E_2^{*}$ 处发生Hopf分支。

下面，我们计算 $d=\bar{d}$ 时的第一个李雅普诺夫系数，它决定Hopf分支的方向。设 $X=x-x_2^{*}$ ， $Y=y-y_2^{*}$ ，我们仍然用x和y分别替换X和Y。那么系统(1.2)变为

$\frac{\text{d}x\left(t\right)}{\text{d}t}=a_{11}x+a_{12}y+f_1\left(x,y\right),\frac{\text{d}y\left(t\right)}{\text{d}t}=a_{21}x+a_{22}y+f_2\left(x,y\right),$

其中

$\begin{array}{l}{a}_{11}=x_2^{*}\left(\beta y_2^{*}-e\right),a_{12}=x_2^{*}\left(1+\beta x_2^{*}\right),a_{21}=-y_2^{*}\left(1+2\beta x_2^{*}\right),a_{22}=-y_2^{*},\\ f_1\left(x,y\right)=\left(1+2\beta x_2^{*}\right)xy+\left(\beta y_2^{*}-e\right)x^2+\beta y{x}^2,\\ f_2\left(x,y\right)=-y^2-\left(1+2\beta x_2^{*}\right)xy-\beta y_2^{*}{x}^2-\beta y{x}^2.\end{array}$

令 $u=y,v=-\frac{a_{21}}{\omega }x-\frac{a_{22}}{\omega }y$ ，其中 $\omega =\sqrt{{\omega }_2}$ ，我们得到

$\frac{\text{d}u\left(t\right)}{\text{d}t}=-\omega v+p\left(u,v\right),\frac{\text{d}v\left(t\right)}{\text{d}t}=\omega u+q\left(u,v\right),$

其中

$p\left(u,v\right)=-\frac{\omega uv}{y_2^{*}}-\beta \frac{{\left(\omega v-y_2^{*}u\right)}^2\left(y_2^{*}+u\right)}{{\left(1+2\beta x_2^{*}\right)}^2{\left(y_2^{*}\right)}^2},$

$\begin{array}{c}q\left(u,v\right)=-\frac{y_2^{*}}{\omega }p\left(u,v\right)+\frac{y_2^{*}\left(1+2\beta x_2^{*}\right)}{\omega }\left[\frac{\omega uv}{y_2^{*}}-u^2+\frac{{\left(\omega v-y_2^{*}u\right)}^2\left(\beta y_2^{*}-e+\beta u\right)}{{\left(1+2\beta x_2^{*}\right)}^2{\left(y_2^{*}\right)}^2}\right]\\ =2\beta x_2^{*}uv-\frac{y_2^{*}\left(1+2\beta x_2^{*}\right)u^2}{\omega }+\frac{{\left(\omega v-y_2^{*}u\right)}^2\left[2\beta x_2^{*}\left(\beta y_2^{*}-e+\beta u\right)-e\right]}{\omega {\left(1+2\beta x_2^{*}\right)}^2{\left(y_2^{*}\right)}^2}.\end{array}$

令

$\mu =\frac{1}{16}\left[p_{uuu}+p_{uvv}+q_{uuv}+q_{vvv}\right]+\frac{1}{16w}\left[p_{uv}\left(p_{uu}+p_{vv}\right)-q_{uv}\left(q_{uu}+q_{vv}\right)-p_{uu}{q}_{uu}+p_{vv}{q}_{vv}\right],$

其中 $p_{uv}$ 表示 $\left({\partial }^{2}p/\left(\partial u\partial v\right)\right)\left(0,0\right)$ ，其他符号也类似。当 $d=\bar{d}$ 时，经过仔细计算，得到

$\begin{array}{c}\mu =-\frac{1}{16{\omega }^2}\{\frac{4{\beta }^2{\omega }^2{x}_2^{*}\left(1+\beta x_2^{*}\right)+4\beta x_2^{*}{y}_2^{*}\left(\beta d-e\right)\left(2+3\beta x_2^{*}\right)}{{\left(1+2\beta x_2^{*}\right)}^3}\\ +\frac{4\beta {\left(x_2^{*}\right)}^2\left[\beta y_2^{*}-e+\beta x_2^{*}\left(\beta d-e\right)\right]}{1+2\beta x_2^{*}}+{\frac{4\beta {\left(y_2^{*}\right)}^2\left(\beta d-e\right)}{{\left(1+2\beta x_2^{*}\right)}^4}\}}_{d=\bar{d}}.\end{array}$

注意到当 $d=\bar{d}$ 时， $\frac{e}{\beta }<\bar{d}<F\left(x_0\right)$ 且 $y_2^{*}>\frac{e}{\beta }$ ，因此得到 $\mu <0$ 。根据Guckenheimer和Holmes [16]

的定理3.4.2和公式(3.4.11)，对于每个分支值 $d=d_1^{*},d_2^{*}$ 和 $d^{*}$ ，Hopf分支都是超临界的。由定理3.5，如果 $\lambda \in {\Lambda }_{2b-1}$ ，则系统发生两次Hopf分支。第一次Hopf分支发生在 $d=d_1^{*}$ 处，并且是向前的；第二次Hopf分支发生在 $d=d_2^{*}$ 处，并且是向后的。如果 $\lambda \in {\Lambda }_{2b-2}$ ，则当 $d=d^{*}$ 时发生向前的Hopf分支。

当 $d=d_1^{*}$ 和 $d=d_2^{*}$ 时系统(1.2)发生Hopf分支， ${x_2^{*}|}_{d=d_1^{*}}={\xi }_2$ 和 ${x_2^{*}|}_{d=d_2^{*}}={\xi }_1$ ，若将 ${\xi }_2$ 和 ${\xi }_1$ 代入 $F\left(x\right)=d$ ，

则可以得到 $d_1^{*}$ 和 $d_2^{*}$ 。即，如果 $\lambda \in {\Lambda }_{2b-1}$ ，则Hopf分支值 $d_1^{*}$ 与 $d_2^{*}$ 可以分别表示为 $d_1^{*}=F\left({\xi }_2\right)$ 与 $d_2^{*}=F\left({\xi }_1\right)$ ，其中， ${\xi }_2$ 和 ${\xi }_1$ 为 $\psi \left(x\right)$ 的正根。类似地，如果 $\lambda \in {\Lambda }_{2b-2}$ ，则Hopf分支值 $d^{*}$ 可表示为 $d^{*}=F\left({\xi }_2\right)$ 。

由于 ${\xi }_1$ 和 ${\xi }_2$ 的表达式含有三角函数(见(3.10))，这导致了Hopf分支值 $d_1^{*},d_2^{*}$ 和 $d^{*}$ 的表达式变得复杂，因此我们更倾向于对这些分支值进行估计。

令 $\lambda =\left(e,\beta \right)\in {\Lambda }_{2b}$ ，考虑内平衡点的稳定性。当 $d=1$ 时，内平衡点记为 $\left(\bar{x},{\varphi }_1\left(\bar{x}\right)\right)$ 。由 $F\left(x\right)=1$ (见(2.1))，得到

$\bar{x}=\frac{-1+\sqrt{\beta -e}}{\beta },$

并通过计算得到

$\psi \left(\bar{x}\right)=\frac{\beta -2e-2\sqrt{\beta -e}}{\beta },{\psi }^{\prime }\left(\bar{x}\right)=-2\left(\beta -e\right)+6\sqrt{\beta -e}-2.$

由定理3.5和4.1以及 $\psi \left(x\right)$ 的性质，得到以下结论：

引理4.2

1. 设 $\lambda \in \left(\beta ,e\right)\in {\Lambda }_{2b-1}$

1) 如果 $\psi \left(\bar{x}\right)>0$ ，则 $d_2^{*}>d_1^{*}\ge 1$ ;

2) 如果 $\psi \left(\bar{x}\right)\le 0$ 且 ${\psi }^{\prime }\left(\bar{x}\right)<0$ ，则 $d_2^{*}>d_1^{*}\ge 1$ ；

3) 如果 $\psi \left(\bar{x}\right)\le 0$ 且 ${\psi }^{\prime }\left(\bar{x}\right)>0$ ，则 $d_1^{*}<d_2^{*}\le 1$ 。

2. 设 $\lambda \in \left(\beta ,e\right)\in {\Lambda }_{2b-2}$ .，如果 $\psi \left(\bar{x}\right)>0$ ，则 $d^{*}<1$ ；如果 $\psi \left(\bar{x}\right)\le 0$ ，则 $d^{*}\ge 1$ 。

接下来我们考虑决定 $\psi \left(\bar{x}\right)$ 和 ${\psi }^{\prime }\left(\bar{x}\right)$ 的符号的参数区域，

1) 首先考虑 $\psi \left(\bar{x}\right)$ 的符号。显然，如果 $e\ge \frac{\beta }{2}$ ，则 $\psi \left(\bar{x}\right)<0$ ；如果 $e<\frac{\beta }{2}$ ，则当且仅当 $\beta -2e>2\sqrt{\beta -e}$

时 $\psi \left(\bar{x}\right)>0$ ，即 $H\left(e\right):=4e^2-4\left(\beta -1\right)e+{\beta }^2-4\beta >0$ 。 $H\left(e\right)$ 有两个实根：

$u_1\left(\beta \right)=\frac{\beta -1-\sqrt{2\beta +1}}{2},u_2\left(\beta \right)=\frac{\beta -1+\sqrt{2\beta +1}}{2}.$

· 当 $2<\beta \le 4$ 时， ${\beta }^2-4\beta \le 0$ ， $u_1\left(\beta \right)\le 0$ ；如果 $0<e<u_2\left(\beta \right)$ ，则 $H\left(e\right)<0$ ，故 $\psi \left(\bar{x}\right)<0$ 。如果 $e>u_2\left(\beta \right)$ ，则 $\psi \left(\bar{x}\right)>0$ 。

· 当 $\beta >4$ 时， $u_1\left(\beta \right)>0$ ；如果 $u_1\left(\beta \right)<e<u_2\left(\beta \right)$ ，则 $H\left(e\right)<0$ ，故 $\psi \left(\bar{x}\right)<0$ 。如果 $e<u_1\left(\beta \right)$ 或 $e>u_2\left(\beta \right)$ ，则 $H\left(e\right)>0$ ，故 $\psi \left(\bar{x}\right)>0$ 。

2) 接着我们考虑 ${\psi }^{\prime }\left(\bar{x}\right)$ 的符号。如果 $\sqrt{\beta -e}<\frac{3-\sqrt{5}}{2}$ 或 $\sqrt{\beta -e}>\frac{3+\sqrt{5}}{2}$ ，则 ${\psi }^{\prime }\left(\bar{x}\right)<0$ 。如果 $\frac{3-\sqrt{5}}{2}<\sqrt{\beta -e}<\frac{3+\sqrt{5}}{2}$ ，则 ${\psi }^{\prime }\left(\bar{x}\right)>0$ 。若 $e<f_1\left(\beta \right)<\beta -2\left(\beta >2\right)$ ，则当 $e<\beta -\frac{7+3\sqrt{5}}{2}\left(\beta >\frac{7+3\sqrt{5}}{2}\right)$ 时， ${\psi }^{\prime }\left(\bar{x}\right)<0$ ；当 $\beta -\frac{7+3\sqrt{5}}{2}<e<f_1\left(\beta \right)\left(\beta >2\right)$ 时， ${\psi }^{\prime }\left(\bar{x}\right)>0$ 。

最后，我们展示 $e=\frac{\beta }{2},e=u_1\left(\beta \right),e=u_2\left(\beta \right),e=f_1\left(\beta \right),e=f_2\left(\beta \right)$ 这五个函数之间的关系(见图4)：

· 显然， $u_1\left(\beta \right)<\frac{\beta }{2}<u_2\left(\beta \right)$ ；

· 记 ${\beta }_0=\frac{7+3\sqrt{5}}{2}$ ， ${\beta }_1=2\left(\sqrt{5}+2\right)\left({\beta }_1>8>{\beta }_0\right)$ 。当 $\beta ={\beta }_1$ 时， $u_1\left(\beta \right)=f_1\left(\beta \right)=\beta -\frac{7+3\sqrt{5}}{2}=\frac{1+\sqrt{5}}{2}$ ，且 $u_1\left(\beta \right)$ 与 $f_1\left(\beta \right)$ 相切。当 $\beta \in \left(2,{\beta }_1\right)$ 时， $f_1\left(\beta \right)>u_1\left(\beta \right)>\beta -\frac{7+3\sqrt{5}}{2}$ ；当 $\beta >{\beta }_1$ 时， $u_1\left(\beta \right)<f_1\left(\beta \right)<\beta -\frac{7+3\sqrt{5}}{2}$ ；

· $u_1\left(\beta \right)-f_2\left(\beta \right)$ 存在唯一的根 ${\beta }_2\approx 24.9386$ 。当 $\beta \in \left({\beta }_0,8\right)$ 时， $f_2\left(\beta \right)<0<\beta -\frac{7+3\sqrt{5}}{2}<u_1\left(\beta \right)$ ；当 $\beta \in \left(8,{\beta }_1\right)$ 时， $f_2\left(\beta \right)<\beta -\frac{7+3\sqrt{5}}{2}$ ；当 $\beta \in \left({\beta }_1,{\beta }_2\right)$ 时， $f_1\left(\beta \right)>u_1\left(\beta \right)>f_2\left(\beta \right)$ ；当 $\beta >{\beta }_2$ ， $u_1\left(\beta \right)<f_2\left(\beta \right)<f_1\left(\beta \right)$ 。

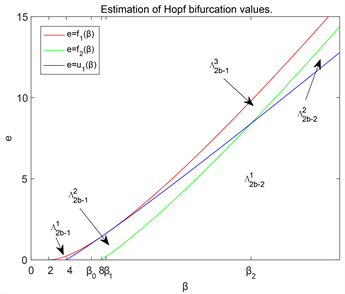
Figure 4. Bifurcation graph of parameter space (β, e)

图4. 参数空间(β, e)分支图

基于上面的讨论，我们将 ${\Lambda }_{2b-1}$ 划分为以下的三个子区域(见图4)：

$\begin{array}{l}{\Lambda }_{2b-1}^1=\left\{\left(\beta ,e\right)\in {\Lambda }_{2b-1}:e<f_1\left(\beta \right)\text{for}\beta \in \left(2,4\right],u_1\left(\beta \right)\le e<f_1\left(\beta \right)\text{for}\beta \in \left(4,{\beta }_1\right)\right\},\\ {\Lambda }_{2b-1}^2=\left\{\left(\beta ,e\right)\in {\Lambda }_{2b-1}:e<u_1\left(\beta \right)\text{for}\beta \in \left(4,8\right],f_2\left(\beta \right)<e<u_1\left(\beta \right)\text{for}\beta \in \left(8,{\beta }_2\right)\right\},\\ {\Lambda }_{2b-1}^3=\left\{\left(\beta ,e\right)\in {\Lambda }_{2b-1}:u_1\left(\beta \right)\le e<f_1\left(\beta \right)\text{for}\beta \in \left({\beta }_1,{\beta }_2\right),f_2\left(\beta \right)<e<f_1\left(\beta \right)\text{for}\beta >{\beta }_2\right\}.\end{array}$

此外，将 ${\Lambda }_{2b-2}$ 划分为以下的的两个子区域(见图4)：

$\begin{array}{l}{\Lambda }_{2b-2}^1=\left\{\left(\beta ,e\right)\in {\Lambda }_{2b-2}:e\le f_2\left(\beta \right)\text{for}\beta \in \left(8,{\beta }_2\right],e<u_1\left(\beta \right)\text{for}\beta >{\beta }_2\right\},\\ {\Lambda }_{2b-2}^2=\left\{\left(\beta ,e\right)\in {\Lambda }_{2b-2}:u_1\left(\beta \right)\le e\le f_2\left(\beta \right)\text{for}\beta >{\beta }_2\right\}.\end{array}$

由引理4.2，可得如下结论：

定理4.3

1) 如果 $\lambda \in {\Lambda }_{2b-1}$ ，则当 $\left(\beta ,e\right)\in {\Lambda }_{2b-1}^1$ 时， $1\ge d_2^{*}>d_1^{*}>\frac{e}{\beta }$ ；当 $\left(\beta ,e\right)\in {\Lambda }_{2b-1}^2$ 时， $d_2^{*}>1>d_1^{*}>\frac{e}{\beta }$ ；当 $\left(\beta ,e\right)\in {\Lambda }_{2b-1}^3$ ，有 $d_2^{*}>d_1^{*}\ge 1$ 。

2) 如果 $\lambda \in {\Lambda }_{2b-2}$ ，则当 $\left(\beta ,e\right)\in {\Lambda }_{2b-2}^1$ 时， $\frac{e}{\beta }<d^{*}<1$ ；当 $\left(\beta ,e\right)\in {\Lambda }_{2b-2}^2$ 时， $d^{*}\ge 1$ 。

5. 结论

本文研究了具有合作捕食和种内竞争的捕食者–食饵模型(1.2)的动力学行为。系统(1.2)中关于 $\left(\beta ,e\right)$ 的参数空间 $\Lambda$ 被划分为若干个不同的区域： $\Lambda ={\Lambda }_1\cup {\Lambda }_2$ ， ${\Lambda }_2={\Lambda }_{2a}\cup {\Lambda }_{2b}$ ， ${\Lambda }_{2b}={\Lambda }_{2b-1}\cup {\Lambda }_{2b-2}$ (见图3)，这种划分对系统(1.2)的动力学行为的分析是非常重要的。在每个区域，随着d的变化，得出了系统(1.2)的动力学行为，其中包括平衡点的个数(见定理2.1、图1和图2)、平衡点的稳定性(见定理3.1和3.5)和

Hopf分支(见定理4.1)。非常有趣的是，随着d在 $\left(\frac{e}{\beta },F\left(x_0\right)\right)$ 中增加，当 $\left(\beta ,e\right)\in {\Lambda }_{2b-1}$ 时，系统(1.2)发生

两次Hopf分支；当 $\left(\beta ,e\right)\in {\Lambda }_{2b-2}$ 时，系统发生一次hopf分支(见定理4.1)。

下面考虑捕食者不存在种内竞争的模型

$\begin{array}{l}\frac{\text{d}x\left(t\right)}{\text{d}t}=x\left(1+\beta x\right)y-dx,\\ \frac{\text{d}y\left(t\right)}{\text{d}t}=y\left(1-y\right)-\left(1+\beta x\right)xy.\end{array}$ (5.1)

Alves和Hilker [13] 的研究结果表明模型(5.1)中最多发生一次Hopf分支，而对于模型(1.2)，当 $\left(\beta ,e\right)\in {\Lambda }_{2b-1}$ 时发生两次Hopf分支，由此可知两次Hopf分支的发生是由捕食者的种内竞争引起的。

如果捕食者不存在合作捕食，那系统(1.2)就成为著名的Volterra-model模型：

$\begin{array}{l}\frac{\text{d}x\left(t\right)}{\text{d}t}=xy-dx-e{x}^2,\\ \frac{\text{d}y\left(t\right)}{\text{d}t}=y\left(1-y\right)-xy.\end{array}$ (5.2)

众所周知，Volterra-model模型(5.2)不会发生Hopf分支。当 $d<1$ 时，系统(5.2)存在唯一的内平衡点

$\left(\frac{1-d}{e+1},\frac{e+d}{e+1}\right)$ ，该平衡点是全局渐近稳定的，这表明了捕食者之间的合作捕食导致了模型(1.2)的振荡行

为。