几类经典不等式在最值问题中的应用探究

Exploration of the Application of Several Classes of Classical Inequalities to the Most Valuable Problems

摘要: 本文首先分析了利用不等式解决的最值问题类型，然后从几何视角归纳了几类经典不等式的特征和关联，接下来将几类经典不等式应用于最值问题的证明与求解当中，并总结了它们的使用场景与应用条件。最值问题的解决方法虽然多样，但是几类经典不等式在解决最值问题中优势明显。

Abstract: This paper first analyzes the types of maximal problems solved by inequalities, then summarizes the characteristics and associations of several types of classical inequalities from the perspective of geometry, and then applies several types of classical inequalities to the proof and solution of the most valuable problems, and summarizes their usage scenarios and application conditions. Although there are various solutions to the maximalist problem, several classes of classical inequalities have obvious advantages in solving the maximalist problem.

1. 引言

最值问题遍及代数、三角函数、立体几何及解析几何等教学内容之中，长期以来是各类考试的热点，且经常作为中考和高考的压轴题，求函数最值的常用方法包括：配方法、不等式法、换元法、数形结合法、函数的单调性法、判别式法。其中，不等关系是客观事物的基本数量关系之一，是数学研究的重要内容之一，也是中学数学中常见的问题类型之一，利用经典不等式解决最值问题是中学数学中常见的解法之一 [1] [2] 。特别是2022年高考理科数学全国甲卷第23题、2022年高考数学全国I卷第18题，利用基本不等式求解最值的解答方法，再次将人们关注的点聚焦于利用不等式解决最值问题。本文首先借助于数形结合，从几何视角来理解几类重要的经典的不等式(均值不等式、柯西不等式、琴生不等式、闵可夫斯基不等式) (一个代数结果的最简单的解释，通常需要借助于几何解释)，然后将这几类不等式应用于最值问题的求解。此外，邹峰等在文 [3] 中将闵可夫斯基不等式用于解决不等式试题。借助于不等式解决数学中的最值问题可以拓展学生逻辑思维，提升学生解决问题的能力，是提高学生数学核心素养的重要途经之一 [4] 。

2. 中学数学中的最值问题

中学数学中的最值问题种类繁多且题型多样，很难用统一的标准进行分类。但是，按照知识领域的分类标准，可以分为几何型最值问题、代数型最值问题、代数几何综合型最值问题，具体分类情况见下图1。

Figure 1. Schematic diagram of maximum value problem classification

图1. 最值问题分类示意图

根据以上关于最值问题的分类，笔者发现，除了使用几何性质进行求解的最值问题之外，涉及度量的最值问题均可以转化为代数式来求解最值。而对于代数式最值问题求解方法的选择，主要依赖于代数式的具体特征，以及构成代数式的运算类型如和或者乘积等等。而下文将要涉及的几类经典不等式又因其各自代数结构的不同而各具特点。下面展示解决最值问题时常用的几类不等式。

3. 几类经典不等式

3.1. 均值不等式

均值不等式是连接算术平均值与几何平均值的一个不等式，揭示了若干个正数的和与积之间的不等关系，其具体形式如下：设 $a_1,a_2,\cdots ,a_n$ 为n个正数，有如下的均值不等式

$\frac{a_1+a_2+\cdots +a_n}{n}\ge \sqrt[n]{a_1{a}_2\cdots a_n}$ ，

当且仅当 $a_1=a_2=\cdots =a_n$ 时等号成立。当 $n=2$ 时，其二元形式为

$\frac{a+b}{2}\ge \sqrt{ab}$ ，或有 $\frac{a^2+b^2}{2}\ge ab$

从左到右依次为平方平均、算术平均、几何平均和调和平均，其几何意义见图2。

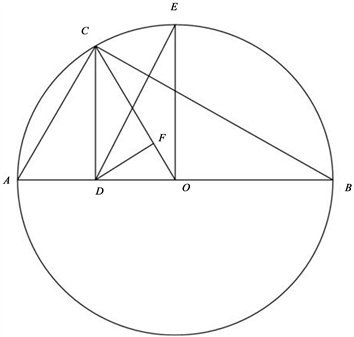
Figure 2. Schematic diagram of the geometric significance of mean inequality

图2. 均值不等式的几何意义示意图

事实上，令 $AD=a,DB=b$ ，则 $AB=a+b$ (直径)， $OC=OE=OB=\frac{a+b}{2}$ (半径)。接下来，有

1) 在 $Rt\Delta ACB$ 中，由射影定理得 $C{D}^2=AD\cdot DB$ ，故 $CD=\sqrt{AD\cdot DB}=\sqrt{ab}$ 。

2) 在 $Rt\Delta DCO$ 中，由射影定理得 $C{D}^2=CF\cdot CO$ ，故 $CF=\frac{C{D}^2}{CO}=\frac{ab}{\frac{a+b}{2}}=\frac{2}{\frac{1}{a}+\frac{1}{b}}$ 。

3) 在 $Rt\Delta DEO$ 中， $OE=\frac{a+b}{2}$ ， $DO=DB-OB=b-\frac{a+b}{2}=\frac{b-a}{2}$ ，所以

$DE=\sqrt{D{O}^2+O{E}^2}=\sqrt{{\left(\frac{b-a}{2}\right)}^2+{\left(\frac{a+b}{2}\right)}^2}=\sqrt{\frac{a^2+b^2}{2}}$ .

在直角三角形中，由于斜边长度 > 直角边长度，所以有

$DE\ge OE=OC\ge CD\ge CF$ ，

故有

$\sqrt{\frac{a^2+b^2}{2}}\ge \frac{a+b}{2}\ge \sqrt{ab}\ge \frac{2}{\frac{1}{a}+\frac{1}{b}}$ .

例1、求函数 $f\left(x\right)=4x^2+\frac{16}{x^2+1}$ 的最小值。

解：利用凑项技巧将原函数化为

$f\left(x\right)=4\left(x^2+1\right)+\frac{16}{x^2+1}-4$ ，

接下来，由均值不等式得

$4\left(x^2+1\right)+\frac{16}{x^2+1}\ge 2\sqrt{4\left(x^2+1\right)\frac{16}{x^2+1}}=16$ ，

所以 $f\left(x\right)\ge 16-4=12$ ，且当 $4\left(x^2+1\right)=\frac{16}{x^2+1}$ ，即 $x=\pm \sqrt{3}$ 时取到等号，此时 $f\left(x\right)$ 取到最小值12。

例2、当 $0<x<4$ 时，求 $f\left(x\right)=x\left(8-2x\right)$ 的最大值。

解：由 $0<x<4$ 知， $8-2x>0$ 。注意到 $2x+\left(8-2x\right)=8$ 为定值，故利用凑系数技巧得

$f\left(x\right)=x\left(8-2x\right)=\frac{1}{2}\left[2x\left(8-2x\right)\right]\le \frac{1}{2}{\left(\frac{2x+8-2x}{2}\right)}^2=8$ ，

且当 $2x=8-2x$ ，即 $x=2$ 时取等号，此时 $f\left(x\right)=x\left(8-2x\right)$ 取到最大值8。

注：

1) 均值不等式的常见结构包括：和与积关系结构、倒数和结构、互为相反数结构、以及复合型结构。均值不等式拥有将“和式”与“积式”互相转换的放缩功能。在求最值时，需充分注意这种转化思想，努力创造可以应用均值不等式的环境。

2) 特别地，如果代数式表示为若干项的代数和，或者若干项的乘积的根式，那么在求该代数式的最值的时候可以考虑使用均值不等式 [5] 。

3) 借助于均值不等式在处理最值问题时，其中的代数式必须为正，且其和或乘积必须为定值。另外还要验证等号是否可以取到。具体解题时，通常需要利用凑项或者凑系数技巧，使之出现和或者乘积为定值的代数结构 [6] 。

3.2. 柯西不等式

柯西不等式又被称为柯西–布尼亚科夫斯基–施瓦兹不等式，其一般形式如下：对于任意两组实数 $a_1,a_2,\cdots ,a_n$ 和 $b_1,b_2,\cdots ,b_n$ ，有

${\left(a_1{b}_1+a_2{b}_2+\cdots +a_n{b}_n\right)}^2\le \left(a_1^2+a_2^2+\cdots +a_n^2\right)\left(b_1^2+b_2^2+\cdots +b_n^2\right)$ ，

其中等号当且仅当 $\frac{a_1}{b_1}=\frac{a_2}{b_2}=\cdots =\frac{a_n}{b_n}$ 时成立。其二维情形为

${\left(ac+bd\right)}^2\le \left(a^2+b^2\right)\left(c^2+d^2\right)$ .

二维情形的几何意义见图3。

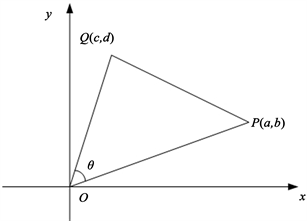
Figure 3. Schematic diagram of the geometric significance of Cauchy inequality

图3. 柯西不等式的几何意义示意图

事实上，由图3得知，

$\left|OP\right|=\sqrt{a^2+b^2}$ ， $\left|OQ\right|=\sqrt{c^2+d^2}$ ， $\left|PQ\right|=\sqrt{{\left(a-c\right)}^2+{\left(b-d\right)}^2}$ .

另外 $\theta$ 表示线段OP与OQ的夹角，则由余弦定理知

${\left|PQ\right|}^2={\left|OP\right|}^2+{\left|OQ\right|}^2-2\left|OP\right|\left|OQ\right|\cos \theta$ ，

从而有

$\cos \theta =\frac{{\left|OP\right|}^2+{\left|OQ\right|}^2-{\left|PQ\right|}^2}{2\left|OP\right|\left|OQ\right|}=\frac{ac+bd}{\sqrt{a^2+b^2}\sqrt{c^2+d^2}}$ .

由于 $0\le {\cos }^2\theta \le 1$ ，故有 ${\cos }^2\theta =\frac{{\left(ac+bd\right)}^2}{\left(a^2+b^2\right)\left(c^2+d^2\right)}\le 1$ ，于是有

${\left(ac+bd\right)}^2\le \left(a^2+b^2\right)\left(c^2+d^2\right)$ .

例3、(2022年高考理科数学全国甲卷第23题)已知 $a,b,c$ 均为正数，且 $a^2+b^2+4c^2=3$ ，证明： $a+b+2c\le 3$ 。

证明：由柯西不等式得到

${\left(a+b+2c\right)}^2\le \left(1^2+1^2+1^2\right)\left[a^2+b^2+{\left(2c\right)}^2\right]$ ，

即 ${\left(a+b+2c\right)}^2\le 3\times 3=9$ ，又因为 $a,b,c$ 均为正实数，所以有 $a+b+2c\le 3$ ，当且仅当 $a=b=2c=1$ 时，等号成立。

例4、求函数 $f\left(x\right)=5\sqrt{x-1}+\sqrt{10-2x}$ 的最大值。

解：因为 $x-1\ge 0$ ，且 $10-2x\ge 0$ ，故函数定义域为 [1] [5] ，且 $f\left(x\right)\ge 0$ 。于是

$\begin{array}{c}f\left(x\right)=5\times \sqrt{x-1}+\sqrt{2}\times \sqrt{5-x}\\ \le \sqrt{\left(5^2+{\left(\sqrt{2}\right)}^2\right)\times \left({\left(\sqrt{x-1}\right)}^2+{\left(\sqrt{5-x}\right)}^2\right)}\\ =6\sqrt{3}\end{array}$

且当x满足 $\frac{5}{\sqrt{2}}=\frac{\sqrt{x-1}}{\sqrt{5-x}}$ 时，即当 $x=\frac{127}{27}$ 时，函数取得最大值，最大值为 $6\sqrt{3}$ 。

例5、空间中一向量 $\stackrel{\to }{a}$ 与x轴，y轴，z轴正向之夹角为 $\stackrel{\to }{\alpha }$ ， $\stackrel{\to }{\beta }$ ， $\stackrel{\to }{\gamma }$ ( $\stackrel{\to }{\alpha }$ , $\stackrel{\to }{\beta }$ , $\stackrel{\to }{\gamma }$ 均非 $\stackrel{\to }{0}$ )，求 $\frac{1}{{\sin }^2\alpha }+\frac{4}{{\sin }^2\beta }+\frac{9}{{\sin }^2\gamma }$ 的最小值。

解：由柯西不等式得

$\begin{array}{l}\left[{\left(\frac{1}{\sin \alpha }\right)}^2+{\left(\frac{2}{\sin \beta }\right)}^2+{\left(\frac{3}{\sin \gamma }\right)}^2\right]\left({\sin }^2\alpha +{\sin }^2\beta +{\sin }^2\gamma \right)\\ \ge {\left(\frac{1}{\sin \alpha }\times \sin \alpha +\frac{2}{\sin \beta }\times \sin \beta +\frac{3}{\sin \gamma }\times \sin \gamma \right)}^2\\ ={\left(1+2+3\right)}^2\end{array}$

另外，因为方向角余弦满足 ${\cos }^2\alpha +{\cos }^2\beta +{\cos }^2\gamma =1$ ，所以有 ${\sin }^2\alpha +{\sin }^2\beta +{\sin }^2\gamma =2$ ，从而有 $2\left(\frac{1}{{\sin }^2\alpha }+\frac{4}{{\sin }^2\beta }+\frac{9}{{\sin }^2\gamma }\right)\ge 36$ ，最终，原式 $\frac{1}{{\sin }^2\alpha }+\frac{4}{{\sin }^2\beta }+\frac{9}{{\sin }^2\gamma }$ 的最小值为18。

注：

1) 柯西不等式的结构简单，形式优美，在最值求解或者不等式证明等有关问题中拥有广泛应用。

2) 如果待处理函数可以恒等变形为：右侧为两个因式之积，其中每个因式均是若干项的平方和；而左侧是右侧中对立项的两两乘积之和的平方，则可以考虑使用柯西不等式 [7] 。

3) 通常利用辅助技巧如配凑系数、添减项、拆常数、凑常值、“1”的代换等技巧，使得包含未知量的平方之和为某一定值 [8] 。

4) 当且仅当等号成立时，目标式才能取得最大值或者最小值 [9] 。

3.3. 琴生不等式

琴生不等式也被称为詹森不等式，是以丹麦数学家约翰·詹森(John Jensen)命名，其具体形式为：

(a) (b)

Figure 4. Function image of upper convex function (left) and lower convex function (right)

图4. 上凸函数(左)、下凸函数(右)的函数图像

1) 若 $f\left(x\right)$ 在区间 $\left[a,b\right]$ 上为上凸函数(见图4)，则有

$f\left(\frac{x_1+x_2+\cdots +x_n}{n}\right)\ge \frac{f\left(x_1\right)+f\left(x_2\right)+\cdots +f\left(x_n\right)}{n}$ ，

当且仅当 $x_1=x_2=\cdots =x_n$ 时，等号成立。

2) 若 $f\left(x\right)$ 在区间 $\left[a,b\right]$ 上为下凸函数(见图4)，则有

$f\left(\frac{x_1+x_2+\cdots +x_n}{n}\right)\le \frac{f\left(x_1\right)+f\left(x_2\right)+\cdots +f\left(x_n\right)}{n}$ ，

当且仅当 $x_1=x_2=\cdots =x_n$ 时，等号成立。

特别地，当 $n=2$ 时，二维情形如下

1) 若 $f\left(x\right)$ 在区间 $\left[a,b\right]$ 上为上凸函数(见图4)，则有

$f\left(\frac{x_1+x_2}{2}\right)\ge \frac{f\left(x_1\right)+f\left(x_2\right)}{2}$ ， (1)

当且仅当 $x_1=x_2$ 时，等号成立。

2) 若 $f\left(x\right)$ 在区间 $\left[a,b\right]$ 上为下凸函数(见图4)，则有

$f\left(\frac{x_1+x_2}{2}\right)\le \frac{f\left(x_1\right)+f\left(x_2\right)}{2}$ ， (2)

当且仅当 $x_1=x_2$ 时，等号成立。

Figure 5. The geometric Meaning of Qinsheng inequality (lower convex function)

图5. 琴生不等式的几何意义(下凸函数)

在这里，我们仅证明(2)式，不妨设 $x_1<x_2$ ，区间 $\left[x_1,x_2\right]$ 的中点为 $\frac{x_1+x_2}{2}$ 。为方便解释，我们假设 $f\left(x\right)>0$ ，由图5知，A点纵坐标为 $f\left(x_1\right)$ ，B点纵坐标为 $f\left(x_2\right)$ ，C点纵坐标为 $f\left(\frac{x_1+x_2}{2}\right)$ 。由几何意义知D点纵坐标为 $\frac{f\left(x_1\right)+f\left(x_2\right)}{2}$ 。从图5可以清楚地发现D点高于C点，即

$f\left(\frac{x_1+x_2}{2}\right)\le \frac{f\left(x_1\right)+f\left(x_2\right)}{2}$ .

事实上，对于任意的下凸函数 $f\left(x\right)$ ，均有不等式(2)成立。

例6、(2018年高考全国卷1理科第16题)已知函数 $f\left(x\right)=2\sin x+\sin 2x$ ，求 $f\left(x\right)$ 的最小值。

解：由于 $f\left(x\right)=2\sin x+\sin 2x$ 是奇函数，周期为 $2\pi$ 。由于其最大值和最小值互为相反数，所以只需要求 $f\left(x\right)$ 的最大值。由于 $f\left(x\right)$ 在区间 $\left[-\frac{\pi }{2},\frac{3\pi }{2}\right]$ 为上凸函数，于是由琴生不等式可得：

$\begin{array}{c}f\left(x\right)=2\sin x+\sin 2x\\ =\sin x+\sin x+\sin \left(\pi -2x\right)\\ \le 3\sin \frac{x+x+\left(\pi -2x\right)}{3}\\ =\frac{3\sqrt{3}}{2}\end{array}$

当且仅当 $\sin x=\sin \left(\pi -2x\right)$ ，即 $x=\frac{\pi }{3}$ 或 $\frac{5\pi }{3}$ 时，等号成立。故函数 $f\left(x\right)$ 的最小值为 $\frac{-3\sqrt{3}}{2}$ 。

例7、已知 $x,y,z$ 均为正数，且满足 $x+y+z=1$ ，求 $\sqrt[5]{x+1}+\sqrt[5]{y+1}+\sqrt[5]{z+1}$ 的最大值。

解：令 $f\left(t\right)=\sqrt[5]{t+1}$ ， $t\in \left(0,1\right)$ ， $f^{″}\left(t\right)=\frac{-4}{25}{\left(t+1\right)}^{-\frac{4}{5}}<0\left(t\in \left(0,1\right)\right)$ ， $f\left(t\right)$ 为区间 $\left[0,1\right]$ 上的上凸函数。由琴生不等式得

$\frac{f\left(x\right)+f\left(y\right)+f\left(z\right)}{3}\le f\left(\frac{x+y+z}{3}\right)$ ，

即

$\frac{1}{3}\left(\sqrt[5]{x+1}+\sqrt[5]{y+1}+\sqrt[5]{z+1}\right)\le f\left(\frac{1}{3}\right)$ ，

从而

$\sqrt[5]{x+1}+\sqrt[5]{y+1}+\sqrt[5]{z+1}\le 3f\left(\frac{1}{3}\right)=\sqrt[5]{324}$ ，

因此 $\sqrt[5]{x+1}+\sqrt[5]{y+1}+\sqrt[5]{z+1}$ 的最大值为 $\sqrt[5]{324}$ 。

例8、(2011年高考湖北卷(理))设 $a_k,b_k\left(k=1,2,\cdots ,n\right)$ 均为正数，证明：

(1) 若 $a_1{b}_1+a_2{b}_2+\cdots +a_n{b}_n\le b_1+b_2+\cdots +b_n$ ，则 $a_1^{b_1}{a}_2^{b_2}\cdots a_n^{b_n}\le 1$ ；

(2) 若 $b_1+b_2+\cdots +b_n=1$ ，则 $\frac{1}{n}\le b_1^{a_1}{b}_2^{a_2}\cdots b_n^{a_n}\le b_1^2+b_2^2+\cdots +b_n^2$ 。

证明：(1) 令 $g\left(x\right)=\ln x\left(x>0\right)$ ，则 $g^{″}\left(x\right)=-\frac{1}{x^2}<0$ ，

所以 $g\left(x\right)$ 在 $\left(0,+\infty \right)$ 上是下凸函数，对于 $\forall a_k\in \left(0,+\infty \right),\left(k=1,2,\cdots ,n\right)$ ，

由琴生不等式：

$\frac{{\displaystyle {\sum }_{k=1}^n{b}_k\ln a_k}}{{\displaystyle {\sum }_{k=1}^n{b}_k}}\le \ln \left(\frac{{\displaystyle {\sum }_{k=1}^n{b}_k{a}_k}}{{\displaystyle {\sum }_{k=1}^n{b}_k}}\right)\le \ln 1=0\left(\because {\displaystyle {\sum }_{k=1}^n{a}_k{b}_k}\le {\displaystyle {\sum }_{k=1}^n{b}_k}\right)$ ，

所以 ${\displaystyle {\sum }_{k=1}^n{b}_k\ln a_k}\le 0$ ，

故 ${\displaystyle {\prod }_{k=1}^n{a}_k^{b_k}}\le 1$ 。

(2) 由(1)知， $g\left(x\right)=\ln x$ 在 $\left(0,+\infty \right)$ 上是下凸函数，由琴生不等式：

对于 $\forall b_k\in \left(0,1\right)$ ，且 ${\displaystyle {\sum }_{k=1}^n{b}_k}=1$ ，

$\frac{{\displaystyle {\sum }_{k=1}^n{b}_k\ln b_k}}{{\displaystyle {\sum }_{k=1}^n{b}_k}}\le \ln \left(\frac{{\displaystyle {\sum }_{k=1}^n{b}_k^2}}{{\displaystyle {\sum }_{k=1}^n{b}_k}}\right)\Rightarrow {\displaystyle {\prod }_{k=1}^n{b}_k^{b_k}}\le {\displaystyle {\sum }_{k=1}^n{b}_k^2}$ ，(*)

对于 $b_k,\frac{1}{b_k}\in \left(0,+\infty \right)$ ，且 ${\displaystyle {\sum }_{k=1}^n{b}_k}=1$ ，

$\frac{{\displaystyle {\sum }_{k=1}^n{b}_k\ln \frac{1}{b_k}}}{{\displaystyle {\sum }_{k=1}^n{b}_k}}\le \ln \left(\frac{{\displaystyle {\sum }_{k=1}^n{b}_k\frac{1}{b_k}}}{{\displaystyle {\sum }_{k=1}^n{b}_k}}\right)=\ln n$ ，

从而 $\ln \frac{1}{{\displaystyle {\prod }_{k=1}^n{b}_k^{b_k}}}\le \ln n$ ，

故 ${\displaystyle {\prod }_{k=1}^n{b}_k^{b_k}}\ge \frac{1}{n}$ ，(**)。

将(*)、(**)综合，可得出原不等式成立。

琴生不等式与函数的上下凸性密切相关，本文仅考察了将琴生不等式应用于最值问题。此外，文 [7] 中将琴生不等式用于不等式的证明中。实际上，函数的上下凸性是高等数学中关于函数的一个重要性质，在高中不做具体要求，但是却经常出现在高考试题中，这也表明了高考命题是源于教材而高于教材的原则，同时也体现了高考是为高校选拔优秀人才的功能性。特别地，2022年高考数学试题难度的加大更凸显了在高中阶段适当超前学习高等数学相关知识的重要性。

注：

1) 琴生不等式描述了积分的凸函数值和凸函数的积分值间的关系。

2) 如果被考察的代数式为形式相同的若干项之和，则可以考虑使用琴生不等式 [10] 。

3) 具体解题时，需根据题设构造满足题意的具有合适凸性的函数，建议结合函数图像来理解，所以在学习时需要提高数形结合的核心素质。

3.4. 闵可夫斯基不等式

向量形式的闵可夫斯基不等式具体形式如下 [11] ：

${\left({\displaystyle {\sum }_{i=1}^n{x}_i^p}\right)}^{\frac{1}{p}}+{\left({\displaystyle {\sum }_{i=1}^n{y}_i^p}\right)}^{\frac{1}{p}}\ge {\left({\displaystyle {\sum }_{i=1}^n{\left(x_i+y_i\right)}^p}\right)}^{\frac{1}{p}}$ ， (3)

其中 $x_i,y_i>0$ ，且 $p\ge 1$ 。当 $n=2,p=2$ 时，(3)式具有如下二维形式

$\sqrt{x_1^2+x_2^2}+\sqrt{y_1^2+y_2^2}\ge \sqrt{{\left(x_1+y_1\right)}^2+{\left(x_2+y_2\right)}^2}$ ， (4)

其取等号条件为 $\frac{x_1}{x_2}=\frac{y_1}{y_2}$ ，其几何意义见图6。

事实上，借助于勾股定理，各线段长度分别为

$AB=\sqrt{x_1^2+x_2^2}$ ， $BC=\sqrt{y_1^2+y_2^2}$ ， $AC=\sqrt{{\left(x_1+y_1\right)}^2+{\left(x_2+y_2\right)}^2}$ .

如果A、B、C三点不共线，则有 $AB+BC>AC$ 。从而，有

$\sqrt{x_1^2+x_2^2}+\sqrt{y_1^2+y_2^2}>\sqrt{{\left(x_1+y_1\right)}^2+{\left(x_2+y_2\right)}^2}$ .

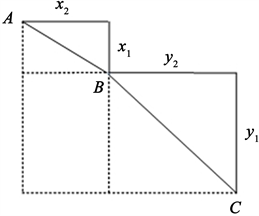
Figure 6. Schematic diagram of the geometric significance of inequality (4)

图6. 不等式(4)的几何意义示意图

另外，如果A、B、C三点共线，于是线段AB、BC具有相同的斜率，即 $\frac{x_1}{x_2}=\frac{y_1}{y_2}$ ，此时有 $AB+BC=AC$ 。综上，不等式(4)成立。

更进一步，重复使用不等式(4)，则得到闵可夫斯基不等式的特例

$\begin{array}{l}\sqrt{x_1^2+x_2^2}+\sqrt{y_1^2+y_2^2}+\sqrt{z_1^2+z_2^2}\\ \ge \sqrt{{\left(x_1+y_1\right)}^2+{\left(x_2+y_2\right)}^2}+\sqrt{z_1^2+z_2^2}\\ \ge \sqrt{{\left(x_1+y_1+z_1\right)}^2+{\left(x_2+y_2+z_2\right)}^2}\end{array}$ (5)

取等号条件为 $\frac{x_1}{x_2}=\frac{y_1}{y_2}=\frac{z_1}{z_2}$ 。不等式(5)的几何意义见图7。此外，邹峰在文 [12] 中将闵可夫斯基不等式用于解决不等式试题。

Figure 7. Schematic diagram of the geometric significance of inequality (5)

图7. 不等式(5)的几何意义示意图

例9、已知函数 $f\left(x\right)=\sqrt{x^2-4x+9}+\sqrt{x^2-6x+11}$ ，求函数的最小值。

解：首先将原函数 $f\left(x\right)$ 进行恒等变形，然后利用(4)式，得到

$\begin{array}{c}f\left(x\right)=\sqrt{{\left(x-2\right)}^2+{\left(\sqrt{5}\right)}^2}+\sqrt{{\left(3-x\right)}^2+{\left(\sqrt{2}\right)}^2}\\ \ge \sqrt{{\left(x-2+3-x\right)}^2+{\left(\sqrt{5}+\sqrt{2}\right)}^2}\\ =\sqrt{1+7+2\sqrt{10}}\\ =\sqrt{8+2\sqrt{10}}\end{array}$

该不等式的几何意义可以参考图6。此外，当 $\frac{x-2}{3-x}=\frac{\sqrt{5}}{\sqrt{2}}$ 时，即当 $x=\frac{11-\sqrt{10}}{3}$ 时，等式成立。所以，函数 $f\left(x\right)$ 的最小值为 $\sqrt{8+2\sqrt{10}}$ 。

此外，借助于闵可夫斯基不等式，还可以处理包含根式与三角函数的复杂函数的最值问题。见下面的例子。

例10、已知一元函数 $f\left(x\right)=\sqrt{13-12\sin x}+3\sqrt{5-4\cos x}$ 的最小值。

解：将原函数进行恒等变形，并借助于闵可夫斯基不等式(4)，得

$\begin{array}{c}\frac{2}{3}f\left(x\right)=\sqrt{{\left(2\cos x\right)}^2+{\left(-2\sin x+\frac{4}{3}\right)}^2}+\sqrt{{\left(4-2\cos x\right)}^2+{\left(2\sin x\right)}^2}\\ \ge \sqrt{{\left(2\cos x+4-2\cos x\right)}^2+{\left(-2\sin x+\frac{4}{3}+2\sin x\right)}^2}\\ =\sqrt{16+\frac{16}{9}}=\frac{4}{3}\sqrt{10}\end{array}$

从而有， $f\left(x\right)\ge 2\sqrt{10}$ 。此外，当 $\frac{2\cos x}{4-2\cos x}=\frac{\frac{4}{3}-2\sin x}{2\sin x}$ 时，即当 $3\sin x+\cos x=2$ 时，等号成立。所以函数 $f\left(x\right)$ 的最小值为 $2\sqrt{10}$ 。

例11、(2021年清华大学丘成桐数学科学领军计划的试题)求以下二元函数的最小值：

$f\left(x,y\right)=\sqrt{4y^2-12y+10}+\sqrt{18x^2+4y^2-12xy+6x-4y+1}+\sqrt{18x^2-18x+5}$ .

解：该不等式的几何意义可参考图6。首先将每个根式进行配方，并利用不等式(5)，得

$\begin{array}{c}f\left(x,y\right)=\sqrt{{\left(3-2y\right)}^2+1^2}+\sqrt{{\left(2y-3x-1\right)}^2+{\left(3x\right)}^2}+\sqrt{{\left(3x-1\right)}^2+{\left(2-3x\right)}^2}\\ \ge \sqrt{{\left(3-2y+2y-3x-1+3x-1\right)}^2+{\left(1+3x+2-3x\right)}^2}\\ \ge \sqrt{1^2+3^2}=\sqrt{10}\end{array}$

且当 $x=0,y=\frac{1}{2}$ 或者 $x=\frac{5}{12},y=\frac{4}{3}$ 时， $f\left(x,y\right)$ 取到最小值 $\sqrt{10}$ 。

注：在使用闵可夫斯基不等式时，需注意

1) 首先将所求原函数进行等价变形为若干个根式之和，然后将每个根式进行配方。

2) 然后再借助于闵可夫斯基不等式进行证明或者求最值。

3) 必要时，可以借助于三角函数公式，以及加项减项技巧，将所考虑的问题转化为几何问题 [11] 。

4) 适当地借助示意图，可以更好地帮助解题。

4. 总结

本文首先从几何视角出发，借助于数形结合来理解几类经典不等式，这种作法可以将一些较为抽象的问题具体化，由抽象思维向具象思维进行转换，有助于学生更好地理解深奥的不等式，也可以促进对题干进行理解和梳理。然后借助于几何意义将不等式用于解决最值问题 [12] 。总之，以几何视角将经典不等式用于最值问题的处理，可有效提升学生的数形结合的能力，拓展学生逻辑思维，并最终提高学生解决问题的能力。另外，希望学生在解决问题的同时，充分将数与形相结合，努力培育观察、猜想、抽象、概括、证明等数学核心素养。