一种改进的A*路径规划算法研究及其Qt实现

An Improved A* Path Planning Algorithm and Its Qt Implementation

摘要: 路径规划算法是人工智能技术中的关键技术之一，常用的A*算法可以在大多数情况下以较快的速度生成路径，但考虑到不同工作环境中最优路径与运行效率不可兼得，为提高现有A*算法的使用灵活度，本文提出了一种加权A*算法，改进了算法的运行时间和搜索准确度。改进后的算法在Qt5.12.9和UOS操作系统环境下进行了实现和测试，结果表明求出最短路径的概率为100%，平均运行时间与传统A*算法相比缩短了12.3%。与标准的A*相关算法相比，提出的改进算法能够缩短规划时间，缩小算法搜索空间，提高算法在路径规划问题中的适用性，提高了不同环境路径生成的效率和平滑性，为运行载体在复杂背景下的精确控制提供了新思路。

Abstract: Path planning algorithm is one of the key technologies in artificial intelligence technology, common A* algorithm can generate road route quickly under most circumstances. Given that it can not achieve the best road route and working efficiency in different working environments at the same time, this paper proposes a weighted A* algorithm, which shortens the running time and enhances search accuracy of the algorithm. The improved algorithm is implemented and tested under Qt5. 12.9 and UOS environment, the results show that the probability of finding the shortest path is 100%, and the average running time is shortened by 12.3%. Compared with the standard A* algorithm, the weighted A* algorithm can shorten the planning time, reduce the search space of the algorithm, and improve the applicability of the algorithm in path planning problems. It improves the efficiency and smoothness of path generation in different environments, and provides a new idea for the precise control of operating vehicles in complex backgrounds.

1. 引言

近年来，随着人工智能技术和云计算的快速发展，智能机器人领域的研究也上升到一个新的高度。其中，路径规划是智能机器人研究领域的关键技术之一，是指智能机器人在真实工作环境中，根据设定的性能指标，寻找一条从起点位置到目标位置的最优路径(如最佳距离时间，无碰撞等等)。移动机器人是一个具有环境感知、路径规划、运动控制和执行等多种功能的综合系统。移动机器人不仅可以接受人类的指令，还可以按照预定的程序自主移动，执行一系列复杂的任务。移动机器人具有巨大的研究价值和发展前景。目前，移动机器人作为家用机器人 [1] 、搜救机器人 [2] 、爆炸物处理机器人在采矿、农业、军事和工业制造等领域的应用越来越广泛 [3] 、潜水机器人、医疗机器人 [4] 等。移动机器人路径规划是指在有障碍物的空间中，对地图等先验信息和传感器感知到的数据进行分析处理，并设计出一种策略用于寻找从起始节点到目标节点的某个路线。索引的最优路径可以保证移动机器人沿路径行动时不会遇到障碍物。A*算法是一种很常用的路径查找和图形遍历算法。它有较好的性能和准确度。其于1968年，由Stanford研究院的Peter Hart，Nils Nilsson和Bertram Raphael发表，它可以被认为是Dijkstra算法的扩展。

A*算法是一种启发式算法，它利用启发信息寻找最优路径。A*算法需要在地图中搜索节点，并设定适合的启发函数进行指导。其缺点是实时性差，每一节点计算量大、运算时间长，而且随着节点数的增多，算法搜索效率降低，而且A*算法并没有完全遍历所有可行解，所得到的结果不一定是最优解。针对这些缺点，本文修改了启发式函数，赋予启发式函数权值，使得g(s)和h(s)的相对大小可控，在特定情况下能够找到最优解，降低搜索空间的数量级。

选用Qt作为实验平台的原因是Qt Creator是一个用于Qt开发的轻量级跨平台集成开发环境。Qt Creator可带来两大关键益处：提供首个专为支持跨平台开发而设计的集成开发环境，并确保首次接触Qt框架的开发人员能迅速上手和操作。即使不开发Qt应用程序，Qt Creator也是一个简单易用且功能强大的IDE。Qt的良好封装机制使得Qt的模块化程度非常高，可重用性较好，对于用户开发来说是非常方便的。Qt提供了一种称为signals/slots的安全类型来替代callback，这使得各个元件之间的协同工作变得十分简单。

2. 相关研究

目前有关智能机器人的路径规划研究还处于初步阶段。规划算法有很多种，比较常用的用于智能机器人路径规划的有Dijkstra算法、BFS算法、A*算法 [5] 、人工势场法、RRT算法、蚁群算法、遗传算法等。具有代表性的识别跟踪算法包括轮廓识别算法、Kalman算法、MeanShift算法、KCF算法、基于深度学习的跟踪识别算法等 [6] 。FAN等 [7] 通过使用MeanShift算法获得微型机器人的位置，并采用A*算法计算最短和最优路径，从而实现螺旋微型游泳机器人的导航和视觉反馈控制；SALEHIZADEH等 [8] 利用RRT算法生成多个机器人的运动路径，使用OpenCV库中的霍夫圆变换得到机器人的中心位置，将视觉伺服应用于微型机器人的路径跟随；HUANG等 [9] 使用移动平均滤波器来获取微型机器人的位置，以此完成微型软体游泳机器人的视觉伺服控制。宋丽君等人针对Q-Learning算法学习效率低、收敛速度慢且在动态障碍物的环境下路径规划效果不佳的问题，提出一种改进Q-Learning的移动机器人路径规划算法 [10] 。张柏鑫等人提出基于深度强化学习的移动机器人动态路径规划算法 [11] 。为了使上述路径规划算法在线实时，需要进一步提高算法的计算速度和规划路径的质量和平滑度，识别和跟踪算法主要获取机器人的位置坐标。目前成熟的识别算法主要是获取目标的位置信息。一般采用水平框进行识别。位置信息的精度不够，而且方向和角度参数，容易迷路。不能在复杂的环境中重新识别。为了实现对微型机器人的精确视觉伺服全闭环控制，不仅需要在各种背景下完成准确识别，还需要准确获取机器人的中心位置信息和角度方位。具有角度信息的旋转目标的时间感知和检测可以为机器人提供更准确的视觉反馈信息。未来，智能机器人在人体等复杂环境中的应用，需要优化路径规划和识别检测算法，以实现对机器人的精确控制 [12] 。

本文针对A*算法提高了生成路径的可靠性，相较于传统算法的不一定“最短”，在牺牲运算速度的情况下可以做到路径最短；同时在紧急决策时也可以牺牲路径准确度，在短时间内生成可行路径。

3. A*算法路径规划及其改进方法

3.1. 算法原理

A*(A-star)算法是一种静态网路中求解最短路径最有效的直接搜索算法。在电子游戏中最主要的应用是寻找地图上两点间的最佳路线。在机器人领域中，A*算法常用于移动机器人路径规划。其算法通过定义满足一定的评估函数，估计各个节点的搜索代价，通过比对寻找到各个节点的最小代价节点，对其最小代价节点进行不断扩展，直至找到最终的目的节点。其一般公式如式(1)所示：

$f\left(s\right)=g\left(s\right)+h\left(s\right)$ (1)

${\displaystyle {\sum }_{i=start}^{k-1}cost\left(s_i,s_{i+1}\right)\left(k\le goal\right)}$ (2)

式中f(s)是节点s的综合优先级。当我们选择下一个要遍历的节点时，我们总会选取综合优先级最高(值最小)的节点。g(s)是节点s距离起点的代价。h(s)是节点s距离终点的预计代价，这也就是A*算法的启发函数。A*算法在运算过程中，每次从优先队列中选取f(s)值最小(优先级最高)的节点作为下一个待遍历的节点。A*算法使用两个集合来表示待遍历的节点，与已经遍历过的节点，这通常称之为open_set和close_set。

1) 在极端情况下，当启发函数h(s)始终为0，则将由g(s)决定节点的优先级，此时算法就退化成了Dijkstra算法。

2) 如果h(s)始终小于等于节点s到终点的代价，则A*算法保证一定能够找到最短路径。但是当h(s)的值越小，算法将遍历越多的节点，也就导致算法越慢。

3) 如果h(s)完全等于节点s到终点的代价，则A*算法将找到最佳路径，并且速度很快。可惜的是，并非所有场景下都能做到这一点。因为在没有达到终点之前，我们很难确切算出距离终点还有多远。

4) 如果h(s)的值比节点s到终点的代价要大，则A*算法不能保证找到最短路径，不过此时会很快。

5) 在另外一个极端情况下，如果h(s)相较于g(s)大很多，则此时只有h(s)产生效果，这也就变成了最佳优先搜索。

A*算法一定能搜索到最优路径的前提条件，即：

$h\left(s\right)\le {\text{cost}}^{*}\left(s,s_{goal}\right)$ (3)

${\text{cost}}^{\text{*}}\left(\text{s},{\text{s}}_{\text{goal}}\right)$ 为当前节点到目标节点的最优距离，满足式(3)的h(s)值越大，则扩展节点越少。为了保证搜索路径的最优性，通常选择启发函数h(s)为曼哈顿距离、对角线距离或者欧几里得距离中的一种，见图1。对于给定的两个位置坐标(xi, yi)、(xj, yj)，它们的曼哈顿距离 、对角线距离 以及欧几里得距离d_e分别如式(4)、式(5)、式(6)所示。

$d_m=\left|x_i-x_j\right|+\left|y_i-y_j\right|$ (4)

$d_d=\max \left(\left|x_i-x_j\right|,\left|y_i-y_j\right|\right)$ (5)

$d_e=\sqrt{{\left(x_i-x_j\right)}^2+{\left(y_i-y_j\right)}^2}$ (6)

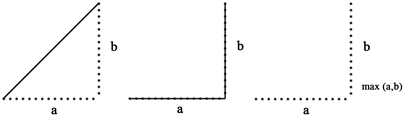
Figure 1. Three different estimated distances

图1. 三种不同的估计距离

3.2. A*算法选择

由于欧几里得的正方先于曼哈顿距离正方向代价相同，而对角线距离代价比曼哈顿距离的对角线距离代价都小，所以使用欧几里得距离仍然可以得到最短的路径，但是会使得A*算法运行时间更久，因此可根据使用利弊进行随机选择欧几里得距离或者曼哈顿距离。本文使用更为普遍的欧几里得距离。在获取欧几里得距离的过程中本文选择获取现实地标的经纬度并进行坐标转换，得到空间直角坐标系下的横坐标(X)和纵坐标(Y)。转化公式为：

$\{\begin{array}{c}X=\left(N+H\right)\ast \text{COS}B\ast \text{COS}L\\ Y=\left(N+H\right)\ast \text{COS}B\ast \text{SIN}L\end{array}$ (7)

其中，B为纬度、L为精度；N为椭圆曲率半径、H为海拔。

3.3. A*算法伪代码

传统A*算法见表1：

Table 1. Traditional A* algorithm pseudocode

表1. 传统A*算法伪代码

3.4. A*算法的改进

假设有一个节点s，如果s的h(s)小于s到终点的实际距离，说明启发函数是小于实际情况的，如果大于，则启发函数是大于实际情况的。很少情况下能得到估计完全准确的启发函数，但我们希望启发函数能尽可能准确。因为启发函数越准确，算法走的“弯路”就越少，需要处理的节点就越少，算法执行速度就越快。

我们知道原本A*算法计算节点f(s)的方式是：

$f\left(s\right)=g\left(s\right)+h\left(s\right)$ (8)

为了调节启发函数，我们现在改用以下式子：

$f\left(s\right)=g\left(s\right)\ast valu{e}_1+h\left(s\right)\ast valu{e}_2$ (9)

当value₁ = 1而且value₂ = 0时，算法就变成了Dijkstra，这时得到的路径是最优的；当value₂ = 1时，就是传统的A*算法，得到的路径还是最优的；当value₂继续增大时，算法会越来越趋近最佳优先搜索，当value₂大到一定程度，启发函数便不再是一致的，得到的路径可能就不是最优的了。根据不同的节点数量和路况选择适当的value₁和value₂可以提高算法整体的运行效率。如果需要路径规划更精确可以适当增大value₁的权重，如果需要运行速度更快可以适当增大value₂的权重。

在A*算法中需要估算h(s)，h(s)估算方法为：

1) 依次遍历s节点相邻节点，计算邻接点与s组成的向量和s与终点组成的向量的夹角，如果夹角大于90度，说明远离终点而去，则不进行搜索；

2) 对于符合条件的邻接点，计算邻接点到终点的欧几里得距离，得到h(s)。

改进后的A*算法需要统计起点周围障碍物数目，周围障碍物数目估算方法为：

1) 遍历s节点的有效邻接点，统计s与目标障碍物向量和s与终点向量夹角；

2) 如果向量夹角小于60度，则统计该障碍物，否则不统计；

3) 统计各方向周围障碍物x。

g(s)为成本函数， $g\left(s\right)=g\left(u\right)+\text{cost}\left(s_i,s_{i+1}\right)$ ，u为s的父节点， $\text{cost}\left(s_i,s_{i+1}\right)$ 为计算成本，修改 $\text{cost}\left(s_i,s_{i+1}\right)$ 为：

$\frac{value1}{x}\ast d_{us}$ (10)

其中：d_us为u到s的距离，x各方向周围障碍物数量，value1为调整参数，h(s)为s节点到终点的欧几里得距离。

加权A*算法见表2：

Table 2. Improved A* algorithm pseudocode

表2. 改进后A*算法伪代码

4. Qt图形界面设计与实现

4.1. 创建应用程序的界面

由于机器人在实际运行中所在的环境较为复杂。为了简化计算，保证模拟的实时性和计算的精确性，本文通过建立栅格地图的方式来模拟实际环境，见图2。地图大小设置为9*9，19*19和45*45三种。

Figure 2. 45*45 Grid

图2. 45*45网格

4.2. 地图设置

起点、终点和障碍物如图3所示，位置由鼠标手动生成。障碍物占总栅格数量的百分比设置为20%左右，为了保证算法规划出路径的一般性，选择起点和终点尽量位于地图的对角线位置。

Figure 3. Starts, ends, and obstacles

图3. 起点、终点和障碍

4.3. 绘制地图

绘制地图其实就是根据相应位置的Item对象的属性，来绘制该网格。网格属性在初始化和设置障碍物时，已经设置完成。构建代码的方法就是判断网格属性是障碍物还是起点，然后直接绘制，见图4。

Figure 4. Drawing path

图4. 绘制路径

4.4. 运行试验

地图绘制好了以后，可以正常进行寻路测试，见图5和图6。寻路直线需要清除原来的路径，避免上次的路径影响。如果发现地图中没有起点和终点，就直接退出，避免造成寻路异常。

Figure 5. Test map

图5. 测试地图

Figure 6. Test mappath

图6. 测试地图路径

5. 性能分析

5.1. 实验环境

采用构造二维点阵地图的方法对算法性能进行测评，试验设备采用macOSBig Sur操作系统，2.3 GHz 八核Intel i9处理器，内存16 GB，集成开发环境使用CLion 2021.2。

5.2. 运行时间测试结果

本文通过编写计时函数对算法实际运行时间做了实际测试，测试采用了5种不同规模的网路地图，规模依次增大。每张地图都采用单点到单点的搜索，然后记录两种算法总的运行时间，见表3。

Table 3. A* algorithm test run time

表3. A*算法测试运行时间

传统算法平均运行时间为0.00489 s，改进后算法平均运行时间为0.00429 s，平均提升率为12.3%。说明在降低value₁的大小后，g(s)权重降低，搜索空间减小，运行速度提高，对于搜索准确度低的场景可以选择适当降低value₁来达到提高运行速度的目的。而且通过观察地图大小对运行效率的影响，地图尺寸越大提升效果越明显。

5.3. 运行准确度测试结果

测试结果见图7、图8和图9：

Figure 7. 9*9 Test result

图7. 9*9测试结果

Figure 8. 19*19 Test result

图8. 19*19测试结果

Figure 9. 45*45 Test result

图9. 45*45测试结果

针对测试情况得出以下结果，见表4：

Table 4. Accuracy test results

表4. 准确度测试结果

传统算法平均路径长度62，改进后算法平均路径长度为50，平均提升率为20%。对于传统A*算法，由于h(s)一直存在，并不能保证规划路线最短，而在改进之后可以成功消除h(s)，在损失时间效率的前提下取得最短路径，满足使用者在不同运行环境的准确度要求。试验中在提高value₁后，g(s)比例上升，算法搜索空间扩大，更容易找到最短路径，对于搜索准确度要求高的场景可以选择适当提高value₁来达到获取最优解的目的。而且通过观察地图大小对搜索准确度的影响，地图尺寸越大提升效果越明显。

综上所述，可以看出在运行时间和运行准确度方面，改进后的A*算法均优于传统A*算法。

6. 结语

经过大量的自制地图模拟试验，与传统A*搜索算法相比，优化后的A*算法路径规划的准确度以及效率都优于前者，改进后的算法在Qt 5.12.9和UOS操作系统环境中经过测试，求出最短路径的概率为100%，平均运行时间较前者缩短12.3%，并且已将改进后的A*算法应用于定制机器人全局路径规划系统中，且在实际应用中表现出良好的稳定性，提高了不同环境路径生成的效率和平滑性，采用改进后的A*算法为运行载体在复杂环境下的精确控制提供了新的可借鉴方法。

基金项目

北京市教育委员会科学研究计划项目(KM20210009002)，大学生创新创业训练计划项目(2023)。

参考文献