风力机波形前缘叶片气动性能及流场特性分析

Analysis of Aerodynamic Performance and Flow Field Characteristics of Wind Turbine Leading Edge Blades

摘要: 针对波形前缘结构可以延缓失速以及改变叶片流场的特性，采用数值模拟方法研究波形前缘叶片的气动性能以及流场特性，获得波形前缘结构对叶片绕流流场的影响规律。结果表明：波形前缘结构可以有效延缓失速的发生，尤其在大攻角下效果更为明显；在前缘波谷处静压变化相较于波峰处更为剧烈，且波峰控制流动效果最佳，波谷处最差。

Abstract: Aiming at the characteristics that the wavy leading edge structure can delay stall and change the flow field of the blade, the aerodynamic performance and flow field characteristics of the wavy leading edge blade are studied by numerical simulation method, and the influence of the wavy leading edge structure on the flow field around the blade is obtained. The results show that the wave leading edge structure can effectively delay the occurrence of stall, especially at high angle of attack. The static pressure change at the leading edge trough is more severe than that at the peak, and the peak control flow effect is the best, and the trough is the worst.

1. 引言

风力机是风电技术发展的关键核心，其运行的实际环境条件较复杂，大气湍流、地面边界层效应等都会严重影响风力机叶片的空气动力性能。为提升风力机气动性能，国内外研究者根据自然界鸟类、鱼类的特征，对风力机进行了大量仿生研究。

Fish F. E和Battle J. M [1] 一起对座头鲸鳍状前肢的水动力性能进行试验测试，并通过风洞试验找出仿生设计应保留的几何特征，将仿生学和机翼的理论研究结合起来。Miklosovic [2] 以NACA0020翼型为原始模型，设计出类似鳍状肢模型叶片，进行吹风试验结果表明，雷诺数在5 × 10⁵左右时，凸起前缘结节可以在降低阻力、增大升力的前提下，延缓失速最大攻角可以提高40%。Pedro，Hugo T. C [3] 和Kobayashi，Marcelo H. [4] 利用数值仿真的方法研究延缓失速的问题，建立与已有实验模型边界条件一致的物理模型，对其进行风洞数值研究，发现波形前缘结构具有提高翼型气动性能的作用。Skillen等人 [5] 采用大涡模拟对波浪前缘翼型进行了数值计算，通过速度等值面的结果表明，光滑前缘翼型发生大面积的前缘分离，而波浪前缘翼型段则表现出明显的分离延迟，同时还可以观察到波峰位置的分离滞后，而波谷的位置分离提前。对于波浪前缘诱导的流向涡对有效攻角的作用，Nierop等人 [6] 在研究座头鲸的结节如何产生延迟失速作用中，做出了相关解释，其中流向涡使得翼型前缘波峰的位置产生一个下洗速度，从而使得翼型的有效攻角降低。陈坤 [7] 将长耳鸮羽毛特征和翅膀的非光滑特性应用到小型轴流风机上，发现仿生叶片能起到良好的导流作用。Yoon H S [8] 发现，在大攻角下，仿生波状前缘能改变翼型前缘的分离线分布，产生纵向涡，从而避免仿生叶片的失速。D Serson [9] 发现波状前缘的翼型能够延缓失速，在大迎角下仍能保持更好的气动性能。姚伟伟 [10] 采用NACA4412翼型作为基本翼型，选择鸮翼前缘凸起结构进行仿生，设计了仿生非光滑前缘风力发电机叶片，利用数值模拟方法，分析了非光滑前缘结构对于风力发电机叶片气动性能影响规律。结果表明：大攻角运行条件下，仿生非光滑前缘风力机叶片能够有效地提高风力机叶片的气动性能，失速角可延迟到10˚左右。

综上所述，前人针对波形前缘结构通过实验以及数值模拟相结合的方法对其进行深入研究，明确了波形前缘结构控制流动及提高气动性能的机理。本文通过座头鲸前缘结节的仿生概念，开展波形前缘对改造的风力机叶片气动性能及流动特性影响的数值研究，进而提高风力机叶片的气动性能。

2. 数学模型及计算方法

2.1. 几何模型

在本文研究工作中选取的数值计算模型是某风力机专用型叶片如图1所示，整个叶片从左到右依次分为圆柱段、过渡段与翼型段三部分。叶片展长R = 1173 mm，叶片最大截面翼型的弦长 $C_0=136\text{mm}$ ，Z为展向位置，最大弦长 $C_0$ 在Z = 19% R处。利用三维建模软件CATIA对该风力机叶片进行波形前缘改型，在以往针对波形前缘结构的研究中，是以叶片为研究对象进行的，主要是通过改变叶片前缘的波长λ和振幅A实现，因此，本研究工作以该风力机叶片光滑前缘为研究对象，对波长λ和振幅A两参数进行组合，其中，图1中已表示波长λ和振幅A两个参数。为了保持叶片前缘的变量统一性，对波长、振幅两个参数进行无量纲化处理：

Figure 1. Waveform leading edge blade modification diagram

图1. 波形前缘叶片改型示意图

$\bar{A}=\frac{A}{C_0}$ (2.1)

$\bar{\lambda }=\frac{\lambda }{R}$ (2.2)

在选择波形前缘的波长和振幅的取值范围过程中，根绝Fish [1] 所给出的座头鲸的鳍肢前缘的凸起分布情况，发现在座头鲸鳍肢的根部位置不存在结节；同时要求波形前缘叶片所选取的波长和振幅均要在座头鲸鳍肢结节的大小范围之内，即 $\bar{A}\in \left[0.025,0.055\right]$ ， $\bar{\lambda }\in \left[0.021,0.078\right]$ 。此外从风力机叶片展向的19%位置起是叶片的翼型段部分，因此在取值范围分别为 $\bar{A}\in \left[0.025,0.055\right]$ 、 $\bar{\lambda }\in \left[0.021,0.078\right]$ 之内选取波长和振幅是合理的。同时，将波长与振幅两个参数均匀地结合起来，获得了两组前缘参数不一致的波形前缘叶片，见表1。图2为三种叶片模型示意图，采用CATIA建模软件进行建模。

(a) 模型

(b) 模型B(c) 模型C

Figure 2. Waved leading edge blade models with different leading edge parameters

图2. 不同前缘参数的波形前缘叶片模型

Table 1. Geometric parameters of the model

表1. 模型几何参数

2.2. 数值计算方法

Navier-Stokes equations方程(N-S方程)可以预测自然界任何流动形式的流动特性。本文流体介质为空气，来流马赫数Ma < 0.3，流体密度变化对流动的影响较小，可视作不可压缩流体。当忽略密度对流体变化的影响时，连续性方程中 $\partial \rho /\partial t=0$ 。这样，本文采用的不可压缩流体雷诺平均N-S方程如下：

$\frac{\partial \left(u_i\right)}{\partial x_i}=0$ (2.3)

$\frac{\partial \left(u_i\right)}{\partial t}+\frac{\partial \left(u_i{u}_j\right)}{\partial x_i}=\frac{1}{\rho }\frac{\partial {\sigma }_{ji}}{\partial x_i}+f_i$ (2.4)

式中：ρ为流体密度，单位为kg/m³；μ为动力粘度，单位为N∙s/m²；t为时间，单位为s； $u_i$ 、 $u_j$ 分别为流体速度在坐标i、j方向的分量，单位m/s，i、j = 1.2.3分别代表x、y、z方向。

图3和图4分别表示计算域示意图以及叶片近壁面网格示意图。计算网格类型为结构化网格，近壁面第一层网格高度为0.02 mm，满足 $y^{+}$ 值小于等于1的要求，网格增长率为1.05。本文在流场计算中使用ANSYS商业软件，流场定常计算采用 $k-\omega SST$ 湍流模型，定常计算结果收敛之后，以定常计算的结果为初始值进行非定常计算，过程采用大涡模拟动力Smagorin-sky-Lilly亚格子模型，计算域大小及边界条件为：叶片最大弦长处的前缘距速度入口处为15C，尾缘距压力出口处为30C，叶片距上下边界为15C。右侧半圆弧以及上下两侧采用速度入口，左侧矩形区域采用压力出口，叶片展向两侧面以及叶片表面定为无滑移壁面。来流速度U₀ = 10 m/s，湍流强度定为3.8%，叶片攻角范围为α = 0˚~12˚，瞬态时间步长设置为2.0 × 10⁻⁵ s，流场计算大约3000时间步之后收敛。

Figure 3. Calculation domain diagram

图3. 计算域示意图

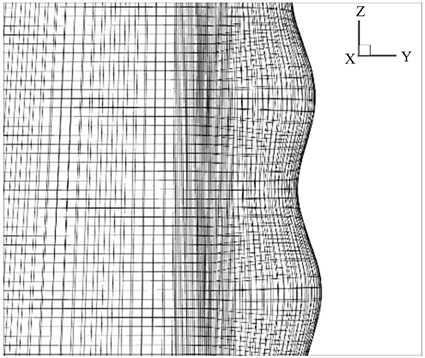
Figure 4. Near wall grid schematic diagram

图4. 近壁面网格示意图

对原始叶片模型进行网格无关性验证，由图5中可知，随着网格数量的不断增加，原始叶片的升阻比呈现逐渐增大的趋势并且趋于稳定。结果表明网格数量在700万~900万内，可以忽略网格数量对结果的影响，本文最终选用738万的网格进行数值模拟计算。

Figure 5. Grid independence verification

图5. 网格无关性验证

3. 结果分析

3.1. 气动性能

为了探究波形前缘结构对叶片气动性能的影响，本文引入升阻力系数及升阻比三种参数探究不同几何参数对波形前缘叶片气动性能的影响。

图6为波形前缘叶片与原始叶片气动性能的对比。从图6(a)可以看出原始叶片随着攻角的增大，升力系数呈增大趋势，随着攻角增大到4˚，升力系数则呈下降趋势，而模型B在0˚~6˚攻角时升力系数呈上升趋势，模型C在0˚~8˚攻角时升力系数呈上升趋势。尤其在大攻角时，波形前缘叶片的升力系数几乎都大于原始叶片，同时，在临界攻角之后，波形前缘叶片升力系数的下降趋势要明显低于原始叶片。相较于原始叶片，波形前缘结构可以有效的延缓失速，对失速后的叶片气动性能也有一定的改善作用。分析不同的几何参数对波形前缘叶片的升力系数的影响可以看出，影响波形前缘叶片升力系数的主要因素是前缘波长，波长越小则升力系数越接近原始叶片，波长越大则在较大攻角下还能提供较高的升力。从图6(b)中可以看出随着攻角的增大，阻力系数呈现先减后增的趋势，临界攻角在4˚攻角。波形前缘叶片在0˚~4˚攻角下阻力系数都大于原始叶片，但随着攻角逐渐变大，波形前缘叶片的阻力系数会逐渐小于同攻角下的原始叶片。其中8˚攻角下，波形前缘叶片的阻力系数由减小转为增大，12˚攻角下，阻力系数差值最大。从图6(c)中可以看出，波形前缘叶片与原始叶片的升阻比的变化趋势较为相同，原始叶片在4˚攻角时达到最高点，之后开始减小，波形前缘叶片在6˚~8˚攻角时由增大变为缓慢减小。

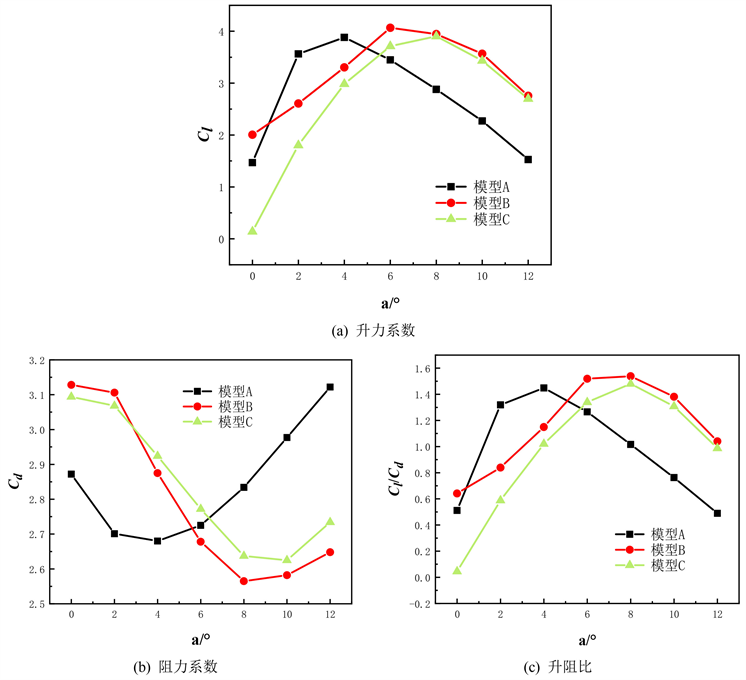
Figure 6. Aerodynamic performance comparison diagram of wave leading edge blade and original blade

图6. 波形前缘叶片与原始叶片的气动性能对比图

综上所述，波形前缘叶片在小攻角下(0˚~6˚)时升力系数相较原始叶片偏小，而阻力系数偏大，以至于升阻比也较大，在大攻角下(6˚~12˚)时，因为失速的延迟导致升力系数还在缓慢上升，而阻力系数的增长率低于原始叶片，故升阻比相较于原始叶片更大一些。故波形前缘结构可以在较大攻角下提高叶片升力，延缓失速，同时降低了阻力系数的增长率，升阻比也随之增大。

图7为6˚攻角下叶片表面静压系数分布图，图8为8˚攻角下叶片表面静压系数分布图，在叶片展向不同切面处，叶片表面静压分布存在明显的差异，在波形前缘叶片波峰Top处，靠近叶片吸力面前缘处，吸力峰消失，叶片表面静压过度平缓，在波形前缘叶片基线Baseline处基本一致，在波形前缘叶片波谷Bottom处，靠近叶片吸力面前缘处，出现尖锐的吸力峰，说明叶片前缘波谷Bottom处静压变化较为剧烈。从整体上看振幅越大，在叶片吸力面波峰Top与基线Baseline处，静压吸力峰更加平缓。

从图中可以看出，原始叶片与仿生叶片的表面压力相接近，但是在叶片前缘处，仿生叶片吸力面的叶片表面压力大于原型叶片，波形前缘叶片在波峰Top、基线Baseline以及波谷Bottom处，吸力面静压吸力峰消失，压力过渡整体较为平缓，更加反应出波形前缘叶片在6˚、8˚攻角下的气动性能较好。

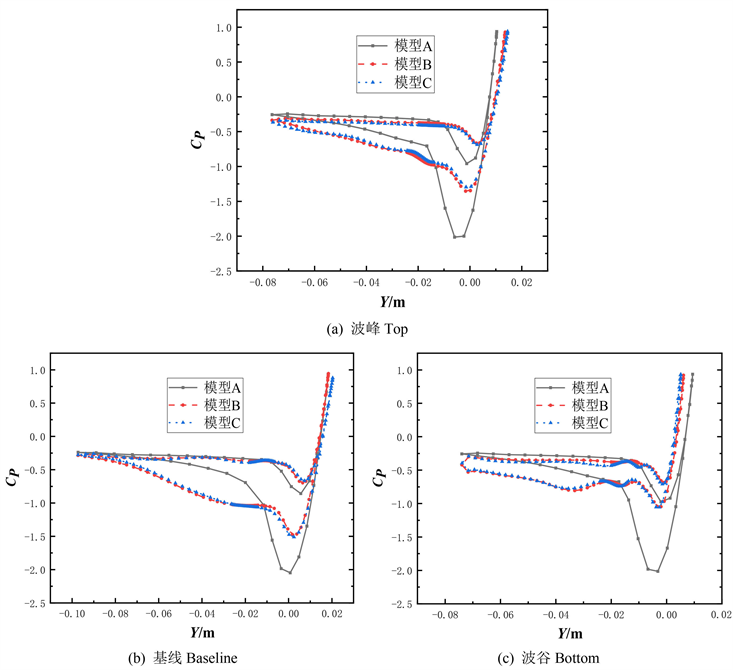
Figure 7. Distribution of static pressure coefficient on blade surface at 6˚ angle of attack

图7. 6˚攻角下叶片表面静压系数分布图

Figure 8. Distribution of static pressure coefficient on blade surface at 8˚ angle of attack

图8. 8˚攻角下叶片表面静压系数分布图

3.2. 流场分析

通过对比6˚攻角下，模型A、模型B和模型C的波峰Top、波谷Bottom以及基线Baseline展向切面速度流线图，探究波形前缘结构对叶片流向流场的影响。

图9表示6˚攻角下叶片在不同切面上的速度流线分布，从图中可以看出，在波峰Top切面处，与原始叶片相比，涡的位置发生了改变，整体上的涡区域范围减小，尤其是模型C。叶片吸力面未出现大范围的低速漩涡区，大涡破碎成小涡，流动分离得到了有效控制。在波谷Bottom切面处与原始叶片相比低速区范围都增大，整体流动状态呈现恶化状态，流动提前发生分离，低速漩涡区以及涡核区域增大。在基线Baseline切面处压力面靠近尾缘处速度也随之增大，而原始叶片未出现这种现象，在较大攻角下，尾缘处的速度增大，叶片尾缘两侧静压差降低，有利于尾缘处不稳定涡的消散。模型B漩涡区范围稍有减小，在叶片吸力面出现附体涡，低速漩涡区域范围减小，但模型C低速区的范围不断扩大且涡核中心逐渐远离叶片。

为了进一步判断波形前缘结构对附面层以及尾流区的涡核心区的影响，需要引入一个分辨漩涡的标准准则对边界层相关结构中的涡旋运动、涡流相互作用进行客观分析，在本文中采取Q准则进行分析。

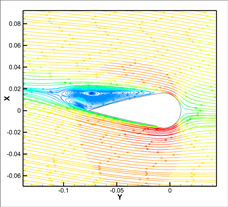
(a) 原型Top (b) 模型B Top (c) 模型C Top

(d) 原型Bottom (e) 模型B Bottom (f) 模型C Bottom (g) 原型 Baseline (h) 模型B Baseline (i) 模型C Baseline

Figure 9. The velocity streamlines at different sections of the blade at 6˚ angle of attack

图9. 6˚攻角下叶片不同切面处速度流线图

图10中根据Q准则计算，给出了t = 0.2 s时刻，模型B以及模型C在6˚攻角下的涡核等值面速度分布。

由图10可得，攻角为6˚时，叶片吸力面产生了大范围三维分离涡，涡度大，叶片位于前缘，由层流向湍流的直接过渡，随流向的开发，涡逐渐变厚，尾缘处涡厚度最大，与尾缘分离时涡的大小增大，波形前缘叶片和原始叶片进行了比较，涡厚度减小，在大小方面没有显着改变。

为了进一步探讨波形前缘叶片绕流的流动机理，本部分将从叶片壁面的极限流线和叶片壁面剪切力两方面来分析，进一步研究波形前缘结构影响绕流流场的作用机制。

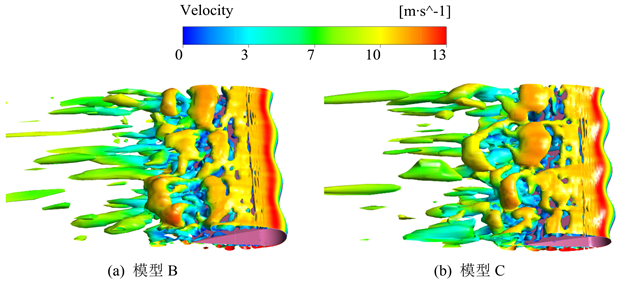
Figure 10. 6˚ angle of attack Q criterion vortex core contour map

图10. 6˚攻角Q准则涡核等值面图

图11为6˚攻角下原始叶片与波形前缘叶片壁面极限流线(模型B与模型C)的比较图，从图中可以得到，原始叶片在壁面展向流动中分离位置基本一致，当波形前缘叶片位于波谷Bottom位置时，产生一组反向涡对，导致流动分离提前，且波峰Top处流线更流畅，从前缘直达尾缘，没有漩涡产生。

(a) 原始叶片 (b) 模型B (c) 模型C

Figure 11. The comparison of the limit streamlines of the original blade and the leading edge blade wall at 6˚ angle of attack

图11. 6˚攻角下原始叶片与波形前缘叶片壁面极限流线对比图

图12是6˚攻角时原始叶片和波形前缘叶片壁面剪切力的比较图(模型B与模型C)，由图可得，原始叶片吸力面壁面剪切力自前缘起呈现逐渐降低趋势，且叶片展向壁剪切力的大小相同，波形前缘叶片在波谷Bottom处的壁面剪切力最大，吸力面波峰Top处受到较大的壁面剪切力，展向呈现周期性的分布模式。

Figure 12. Comparison of wall shear force between original blade and leading edge blade at 6˚ angle of attack

图12. 6˚攻角下原始叶片与波形前缘叶片壁面剪切力对比图

由上面的分析可得，波形前缘结构使得叶片吸力面的壁面位置和壁面的法向位置出现反向涡对，且远离吸力面壁面存在分离涡，使原始叶片展向一致性发生变化，从而使得原始叶片流场结构发生变化，波峰Top处壁面剪切力较大说明此处壁面的气流受到的剪切力较大，波峰将气流导向波谷，并混入主流，造成壁面剪切力大，到了波谷后，流向相同，进而说明波谷处壁面剪切力较低的原因。反向涡对的存在对顺流流动稳定有利，展向涡发展受到抑制，叶片绕流给流动反馈回路增加了阻力，在尾迹的作用下被削弱，流动更平稳，从而使波形前缘叶片在大攻角时仍可维持较大升力。

4. 结论

本章通过流场数值模拟计算，研究了波形前缘叶片的气动特性及流场特性，通过分析获得以下结论：

1) 波形前缘叶片在小攻角下(0˚~6˚)时升力系数相较原始叶片偏小，在大攻角下(6˚~12˚)时，因为失速的延迟导致升力系数还在缓慢上升，波形前缘结构可以在较大攻角下提高叶片升力，有效延缓失速的发生，同时降低了阻力系数的增长率，升阻比也随之增大。

2) 在叶片展向不同切面处，叶片表面静压分布存在着明显的差异，在波形前缘叶片波峰切面以及基线切面，叶片表面静压过度平缓，在波形前缘叶片波谷处，出现尖锐的吸力峰，说明叶片前缘波谷处静压变化较为剧烈。

3) 在大攻角下，波形前缘叶片波峰切面推迟分离能力最大，波谷会提前分离。与原始叶片相比，波形前缘叶片波峰处的控制流场效果最好，波谷控制效果最差。

4) 反向涡对的存在对顺流流动稳定有利，展向涡发展受到抑制，叶片绕流给流动反馈回路增加了阻力，在尾迹的作用下被削弱，流动更平稳，从而使波形前缘叶片在大攻角时仍可维持较大升力。

参考文献