部分函数型数据的回归模型与应用

Regression Models and Applications for Partially Functional Data

摘要: 随着科技的不断发展，各种类型的数据不断涌现，与传统的离散数据相比，函数型数据可以更好地反映出数据的连续性和变化趋势。在实际应用中，我们通常需要根据函数型数据的特征来建立模型。针对响应变量为标量型，预测变量包含函数型和标量型的情况，传统的线性模型已经不能满足需求，为此，本文提出了一种广义部分函数型线性模型，它不仅可以处理标量型和函数型的复合变量，还能够通过预测变量和响应变量之间的关系来估计连接函数，更加符合实际情况。具体来说，本文采用函数型主成分分析方法对函数型变量进行降维，然后利用最大似然估计法对回归系数进行估计，通过局部线性回归的方法对连接函数进行估计，这样我们就可以得到最终的估计值，从而实现对复合变量的建模和预测。为了验证该模型的有效性，本文将其应用于人口密度的研究中。结果表明，该模型可以有效地反应预测变量和响应变量之间的关系，得到了符合预期的结论。这项研究也使得广义部分函数型线性模型有了进一步的应用推广。

Abstract: With the development of technology, various types of data are emerging. Compared with traditional discrete data, functional data can better reflect the continuity and trend of data. In practical appli-cations, we usually need to establish models based on the features of functional data. For the case where the response variable is scalar and the predictor variable contains both functional and scalar variables, traditional linear models cannot meet the requirements. To address this issue, this paper proposes a generalized partially functional linear model, which can not only handle scalar and func-tional composite variables but also estimate the link function through the relationship between the predictor and response variables, making it more practical. Specifically, this paper uses the func-tional principal component analysis method to reduce the dimension of functional variables, and then estimates the regression coefficients using the likelihood estimation method and the link function using the local linear regression method. In this way, we can obtain the final estimate and achieve modeling and prediction of composite variables. To verify the effectiveness of the model, this article applies it to the study of population density. The results show that the model can effec-tively reflect the relationship between the predictor and response variables and obtain expected conclusions. This study also promotes the further application and promotion of the generalized par-tially linear functional linear model.

1. 引言

为了弥补线性回归模型的不足，1972年Nelder和Wedderburn [1] 正式引入了广义线性模型(Generalized Linear Models, GLMs)，相较于线性模型，广义线性模型弱化了对响应变量的要求，即响应变量仅需满足指数分布族即可。Weisberg和Welsh [2] 、Chiou和Muller [3] 、Bai等人 [4] 、Yuan和Diao [5] 等人也都提出了不同的方法，来对连接函数未知的广义线性模型进行探究。

1982年，Ramsay [6] 首次较为明确地提出了函数型数据，并为函数型数据分析的发展奠定了坚实的基础。函数型线性回归模型是函数型数据分析应用较为广泛的方法，它将预测变量的离散观测值转化为光滑的函数，再通过这些函数型数据考虑对于响应变量的影响。对于预测变量既包含函数型变量又包含标量型变量的情况，Zhang [7] 将该模型称为部分函数型线性回归模型，并提出了一种两阶段的方法。Shin [8] 使用基于函数型主成分分析(FPCA)的最小二乘估计方法研究该回归模型的估计和预测。对于部分函数型线性回归模型的预测能力也是近年来不断需要探索的内容，为了更好地提高模型的预测准确性，研究者们对其研究方法进行不断的改进，努力消除可能会使数据过度拟合的问题。Shin和Lee [9] 用岭回归估计方法对部分函数型数据线性回归模型的估计和预测进行了探讨。Lingetal [10] 对于部分函数型数据线性回归，提出了KNN方法，并将此方法和其他方法进行了比较。

函数型广义线性回归模型是函数型线性回归模型的推广。其中广义线性模型既可用于刻画连续型变量，也可用于刻画离散型变量，这使得其具有更广阔的应用领域。James [11] 将函数型自变量加入到广义线性模型中。Müller [12] 等人提出了广义函数性回归模型的一种渐进理论，通过广义协方差算子的方法，获得了确定模型的参数渐近正态性及置信区间。Shang和Cheng [13] 提出了一种广义泛函线性模型非参数推理的粗糙正则化方法。函数型广义线性回归模型最初主要考虑了线性模型，但是实际数据中非线性关系可能更为复杂。因此，近年来的学者们也逐渐开始探索如何建立更加准确的非线性模型。Wong [14] 等人研究了多元预测变量的参数和非参数估计来预测标量型响应变量，该方法可以处理多元函数型数据，并考虑了非线性部分的影响，提高了模型的拟合能力和预测能力。

本文将相关研究中的未知连接函数的广义线性模型与部分函数型线性模型相结合，在以上研究内容的基础上，讨论了连接函数未知的广义部分函数型线性模型，分别得出其相对应的回归系数、连接函数的估计，并带入实例对模型进行验证。在应用部分，本文考察了人口密度的影响因素。人口密度是人口分布的一个重要指标，可以反映出一个地区的人口数量和空间利用状况。本文分别从空气质量指数、年平均收入、接受高等教育的学生数和各市医院总床位数4个方面，即环境、经济、教育和医疗四个方面，运用搭建的模型来对人口密度的影响因素进行探讨。通过深入分析这些因素，可以帮助城市在规划和发展中，更好地考虑人口密度的合理分布的问题，以此来保障城市的可持续发展和居民的生活质量。

2. 广义部分函数型线性模型

2.1. 模型构建

我们给定一组由响应变量 $Y_i$ ，函数型预测变量 $X_{ij}\left(t_j\right)$ 和标量型预测变量 $Z_i$ 构成的独立同分布的观测数据集 $\left(Y_i,X_{ij}\left(t_j\right),Z_i\right),i=1,\cdots ,n;j=1,\cdots ,d$ 。其中响应变量 $Y_i$ 是服从指数分布族，在本文中的应用中，响应变量 $Y_i$ 服从伯努利分布；对于预测变量来说， $X_{ij}\left(t_j\right)$ 表示的是一组属于函数空间 $L^2\left(T_j\right)$ 中的函数型数据， $Z_i$ 是q维向量形式的数据，即 $Z_i={\left(z_{i1},z_{i2},\cdots ,z_{iq}\right)}^{\text{T}}$ 。

建立一个模型去描述响应变量和预测变量之间的关系，即建立 $Y_i$ 与 $X_{ij}\left(t_j\right)$ 和 $Z_i$ 之间的模型：

$Y_i=g\left({\displaystyle \underset{j=1}{\overset{d}{\sum }}{\displaystyle {\int }_{T_j}{X}_{ij}\left(t_j\right){\beta }_j\left(t_j\right)\text{d}{t}_j}}+Z_i\gamma \right)+{\epsilon }_i$ (1)

其中， ${\beta }_j(\cdot )$ 是函数型预测变量 $X_{ij}\left(t_j\right)$ 需要估计的回归系数函数； $\gamma$ 是标量型预测变量 $Z_i$ 需要估计的q维向量形式的回归系数，即 $\gamma ={\left({\gamma }_1,{\gamma }_2,\cdots ,{\gamma }_q\right)}^{\text{T}}$ 。定义一个线性算子 $\eta$ ，且其满足 $\eta ={\displaystyle \underset{j=1}{\overset{d}{\sum }}{\displaystyle {\int }_{T_j}{X}_j}}\left(t_j\right){\beta }_j\left(t_j\right)\text{d}{t}_j+Z\gamma$ 。通过 $g(\cdot )$ 建立了响应变量 $Y_i$ 与线性算子 $\eta$ 之间的关系，即 $E\left[Y|X_j\left(t_j\right),Z\right]=\mu =g\left(\eta \right)$ ，其中 $g(\cdot )$ 又被称为连接函数，本文中 $g(\cdot )$ 是未知的。 ${\epsilon }_i$ 为独立随机误差变量，其中 ${\epsilon }_i=Y_i-g\left(\eta \right)$ ，且满足 $E\left[{\epsilon }_i|X_{ij}\left(t_j\right),Z_i\right]=0$ 。

设 ${\sigma }^2(\cdot )$ 为一个方差函数。 $\exists {\sigma }^2(\cdot )$ ， $\forall c>0$ ， ${\sigma }^2(\cdot )\ge c>0$ ，使得

$Var\left[Y|X_j\left(t_j\right),Z_i\right]={\sigma }^2\left(\mu \right)={\sigma }^2(g(\; \eta \; ))$

$Var\left[{\epsilon }_i\right]=E\left[{\epsilon }_i^2\right]={\sigma }^2\left(E\left[Y|X_j\left(t_j\right),Z\right]\right)$

对于函数型预测变量 $X_{ij}\left(t_j\right)$ ，我们需要对其进行降维。本文采用FPCA的方法，将函数型数据维度降低到几个主成分上，通过保留数据的主要变化趋势，从而更方便的对数据进行分析。首先，我们需要对原始数据进行中心化处理，即每个数据减去其整体均值，使得 $E\left[X_{ij}\left(t_j\right)\right]=0$ ，以此来消除数据的整体偏移。设在函数空间 $L^2\left(T_j\right)$ 中存在一组正交基 ${\rho }_{jk}(\cdot ),k=1,2,\cdots$ ，且满足 ${\displaystyle {\int }_{T_j}{\rho }_{jk}^2\left(t_j\right)\text{d}{t}_j}=1$ 。我们使用Karhunen-Loeve (KL)展开的方法 [15] ，将函数型数据投影到正交基 ${\rho }_{jk}(\cdot )$ 上，即将 $X_{ij}\left(t_j\right)$ 及其回归系数函数 ${\beta }_j(\cdot )$ 分解成：

$X_{ij}\left(t_j\right)={\displaystyle \underset{k=1}{\overset{\infty }{\sum }}{\xi }_{ijk}{\rho }_{jk}\left(t_j\right)}$ (2)

${\beta }_j\left(t_j\right)={\displaystyle \underset{k=1}{\overset{\infty }{\sum }}{a}_{jk}{\rho }_{jk}\left(t_j\right)}$ (3)

其中， ${\xi }_{ijk}$ 为函数型主成分得分，它代表了每个原始数值在正交基 ${\rho }_{jk}(\cdot )$ 上的投影值，即 $X_{ij}\left(t_j\right)$ 在低维函数空间中的坐标。

将上述 $X_{ij}\left(t_j\right)$ 及其回归系数函数 ${\beta }_j(\cdot )$ 的关系式(2)、(3)带入式(1)，可以简化响应变量和预测变量之间的模型。但是由于KL展开后的结果仍是无穷维的函数空间，在实际的应用中，我们通过将函数型数据在m处截断，将 $X_{ij}\left(t_j\right)$ 降到m维空间，其中m为正整数，且 $m<\infty$ 。则模型(1)可表示为：

$Y_i=g\left({\displaystyle \underset{j=1}{\overset{d}{\sum }}{\displaystyle \underset{k=1}{\overset{m}{\sum }}{\xi }_{ijk}{a}_{jk}+Z_i\gamma }}\right)+{\epsilon }_i$ (4)

2.2. 回归系数和连接函数的估计

定义一个参数向量 $\theta$ ，其中

$\theta ={\left(a_{j1},a_{j2},\cdots ,a_{jm},{\gamma }_1,\cdots ,{\gamma }_q\right)}^{\text{T}},j=1,2,\cdots ,d$

对于回归系数 $\theta$ 和连接函数g的估计，我们采用一种复合迭代估计的方法来得到最终的估计值，即假设一个参数保持已知的情况下，对另外一个未知的参数进行估计。下面简单叙述整体的迭代过程：

1、假设连接函数已知情况下，通过加权最小二乘法求解方程(5)，可以得到 $\theta$ 一个初始估计值 ${\theta }^{\left(0\right)}={\left(a_{jk}^0,{\gamma }_q^0\right)}^{\text{T}}$ 。

$U\left(\theta \right)={\displaystyle \underset{i=1}{\overset{n}{\sum }}\left(Y_i-{\mu }_i\right)\frac{g^{\prime }\left({\eta }_i\right)}{{\sigma }^2\left({\mu }_i\right)}{\Delta }_i}=0$ (5)

其中 ${\eta }_i={\displaystyle \underset{j=1}{\overset{d}{\sum }}{\displaystyle \underset{k=1}{\overset{m}{\sum }}{\xi }_{ijk}{a}_{jk}+Z_i\gamma }}$ ， ${\mu }_i=g\left({\eta }_i\right)$ ，且 ${\Delta }_i={\left({\xi }_{ij1},{\xi }_{ij2},\cdots ,{\xi }_{ij{p}_j},z_{i1},\cdots ,z_{iq}\right)}^{\text{T}}$ 。

2、定义一个核函数 $k_h(\cdot )=h^{-1}k\left(\cdot /h\right)$ ，为了简化表达，我们令 $g=g\left(u;\theta \right)$ ， $g^{\prime }=g^{\prime }\left(u;\theta \right)$ 。运用局部线性回归的方法，得到g和 $g^{\prime }$ 的一个初始估计值 $g^{\left(0\right)}$ 和 ${g^{\prime }}^{\left(0\right)}$ ，即使得 $g^{\left(0\right)}$ 和 ${g^{\prime }}^{\left(0\right)}$ 的加权平方和最小

$\left(g^{\left(0\right)},{g^{\prime }}^{\left(0\right)}\right)=\arg \underset{\left(g^{\left(0\right)},{g^{\prime }}^{\left(0\right)}\right)}{\min }{\left[Y_i-g-g^{\prime }\left({\eta }_i^{\left(1\right)}-u\right)\right]}^2{k}_h\left({\eta }_i^{\left(1\right)}-u\right)$ (6)

3、运用1的方法，将连接函数替换为估计后的连接函数 $g^{\left(\omega \right)}$ 和 ${g^{\prime }}^{\left(\omega \right)}$ ，其中 $\omega =0,1,2,\cdots$ 。由此我们可以得到 $\theta$ 的估计值 ${\theta }^{\left(\omega \right)}={\left(a_{jk}^{\omega },{\gamma }_q^{\omega }\right)}^{\text{T}},\omega =1,2,3,\cdots$ 。

4、运用2的方法，将回归系数替换为估计后的 ${\theta }^{\left(\omega \right)}={\left(a_{jk}^{\omega },{\gamma }_q^{\omega }\right)}^{\text{T}}$ ，其中 $\omega =1,2,3,\cdots$ 。由此我们可以得到g和 $g^{\prime }$ 的估计值 $g^{\left(\omega \right)}$ 和 ${g^{\prime }}^{\left(\omega \right)}$ ，其中 $\omega =1,2,3,\cdots$ 。

5、重复上述步骤，直到 $\left|{\theta }^{\left(\omega +1\right)}-{\theta }^{\left(\omega \right)}\right|$ 以及 $\left|g^{\left(\omega +1\right)}-g^{\left(\omega \right)}\right|$ 收敛时，停止迭代。

6、最终得到回归系数 $$ 的估计值 $\hat{\theta }$ ，连接函数g的估计值 $\hat{g}$ 。

3. 人口密度的探究

3.1. 数据来源

我们从国家环监总站收集了各市的空气质量指数(AQI)，从各地区统计公报和中国城市统计年鉴中收集了各市的年平均收入、接受高等教育的学生数、各市医院总床位数，从国家统计局公布的第七次人口普查的数据中通过进一步处理得到的各个城市人口密度。将上述数据应用于我们提出的广义部分函数型线性模型，从环境、经济、教育和医疗四个方面来研究其对于各市人口密度的影响，理论上来说如果当地生态环境、经济、教育和医疗水平越好，该地区的人口密度也应越大。

3.2. 应用

响应变量是由第七次人口普查中的常住人口数据与该市的面积相除而得到的人口密度(人/平方公里)。本文对50个城市的人口密度进行了相应划分：当人口密度值大于700时，我们用1来表示，即该市人口密度较大；当人口密度值小于700时，用0来表示，即该市人口密度较小，以此来使得响应变量服从伯努利分布。在我们的研究中，有25个城市人口密度较大，25个城市人口密度较小。

函数型预测变量AQI是2020年1月1日至2020年12月31日，50个城市共计366天的每日空气质量指数。图1为50个城市AQI每日变化情况。在处理数据时，首先需要将这些数据进行中心化处理；在此案例中，我们选择累计贡献率达到75%的函数型主成分基，即需要选择 $m=9$ 作为标准正交基的截断个数。

Figure 1. Daily AQI changes in 50 cities

图1. 50个城市每日AQI变化图

空气质量对人体的健康有着非常关键的作用。较好的空气质量可以降低空气中有害物质的浓度，减少人体暴露在有害物质中的时间和程度，从而降低呼吸系统、心血管系统等多种疾病的发生率；也可以让人们感到舒适和愉悦，有助于缓解压力和焦虑，提高人们的精神状态，减少抑郁、焦虑等心理问题的发生率。图2中，红色的线表示的是回归系数 $\beta \left(t\right)$ 的估计值 $\hat{\beta }\left(t\right)$ ，灰色的区域表示的是其95%置信区间。通过观察该图，我们可以看出，空气质量指数与人口密度整体是呈负相关的，即空气质量指数的值越高，空气质量越不好，该地区人口密度越低。但在4月中至9月中旬出现了正相关的情况，主要是因为存在的一些外部影响因素 [16] 。首先，春天和秋天是非常适宜旅游的季节，再加上暑假学校放假，许多学生和家长会选择一些去城市旅游或居住，其间增加的一些公共交通的使用量和垃圾产生量等，都可能导致空气质量下降，但却使得人口密度增加；其次，这段时间气温较暖，湿度增大，这样的天气条件有利于光化学反应的发生，使得空气中的臭氧等有害物质浓度上升，尤其是在夏天时，炎热的天气会使得人们更加依赖空调等设施，导致能源消耗增加，进一步加剧空气污染，因此人口聚集越多的城市，污染越严重。

通过观察表1，我们可以发现：年平均收入水平与人口密度呈正比，即收入较高的城市，人口密度也相应较大。通常来说，年平均收入反映了一个地区的经济繁荣程度和人民的生活水平，较高的收入意味着该地区往往有更好的就业机会、更好的社会保障，以及更好的教育和文化资源，这些因素可以吸引更多的人前往这些城市居住和工作，从而导致人口密度的增加。与此同时，较高的收入还能够带动地区的经济发展，促进产业升级和创新，提高生产效率和竞争力，从而形成良性的经济循环，这也可以进一步推动人口密度的增加。

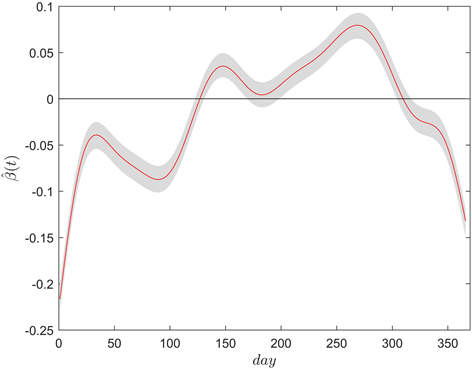
Figure 2. Regression parameters function $\hat{\beta }\left(t\right)$ and its 95% confidence intervals

图2. 回归系数函数 $\hat{\beta }\left(t\right)$ 的估计值及其95%置信区间

高等教育是更高层次的教育和学术研究的教育阶段，通过探究一个城市高等教育的学生数，可以间接地反映出当地的教育综合水平。高等教育的学生数与人口密度呈正比，即高等教育的学生数越多，教育资源越好，就可以吸引更多的人才，同时也吸引更多人前来此地定居，从而促进了人口密度的增长 [17] 。

医院床位数与各城市人口密度也成正比。较多的医院床位数，意味着医院有更多的机会可以提供更好的医疗服务，增加医疗资源的供给量；反之，如果一个医院的医疗水平较高，则该医院也会相应的有较多的床位。所以，一个城市的医院总床位数也是衡量一个城市的医疗水平的重要指标之一。医疗资源丰富，医疗设备齐全，可以吸引患者前往该地区就医，同时也吸引了医疗从业人员前往该地区工作，从而导致人口密度也相应较高。

Table 1. The scalar regression coefficient γ ^ and significance level

表1. 标量型回归系数 $\hat{\gamma }$ 及显著性水平

4. 结论

本文通过函数型主成分分析对高维数据进行降维，提出了未知连接函数的广义部分函数型线性模型，并简单叙述了模型中回归系数和连接函数的估计方法，同时也给出了广义部分函数型线性模型在人口密度上的应用。通过收集2020年中国50个地级市的每日空气质量指数、人均年收入、普通本专科学生数和各市医院总床位数，探究环境、经济、教育、医疗水平对于人口密度的影响。研究表明：空气质量指数与人口密度总体上呈负相关，但是受一些外部因素的干扰，也会在4月至9月呈现正相关；各地人均年收入、普通本专科学生数和各市医院总床位数都与人口密度呈正相关的结论，也符合我们的预期。

基金项目

北方工业大学毓杰人才项目，No. 107051360023XN075-04。