基于决策树算法的长沙市空气质量研究

Research on Air Quality in Changsha City Based on Decision Tree Algorithm

摘要: 本文针对长沙市空气质量问题，运用k近邻算法和决策树算法的理论方法，构建了空气质量预测模型。建立模型并进行求解，通过算法得到空气污染的主要影响因素并且从精准预测了长沙市的空气质量。最后，对模型进行了分析和评价。

Abstract: Aiming at the air quality problem of Changsha City, this paper constructs the air quality prediction model by using the theoretical methods of the k-Nearest Neighbors (k-NN) and Decision Tree Al-gorithm. The model was established and solved, the main influencing factors of air pollution were obtained through the algorithm, and the air quality of Changsha City was accurately predicted. Fi-nally, the model is analyzed and evaluated.

1. 引言

长沙市作为湖南省省会城市，其环境空气质量对城市形象以及旅游业发展有着十分重要的作用。随着我国对环境问题越来越重视，长沙市的空气质量得到了明显的改善，但是仍然有着许多改进的地方，与其他省会城市相比，长沙的空气质量不容乐观。因此，对长沙市环境空气质量进行全面系统的研究，明确长沙环境空气质量的定位，了解相关影响因素并进行合理的预测与诊断，预测空气质量对即将可能出现的空气质量问题进行预防和治理，同时为制定污染控制措施提供一定的科学依据，对于长沙经济的发展具有重要意义。

关于空气质量预测、诊断的研究，目前已经有很多普遍的预测模型。如陈珊子构建灰色预测模型，分析了广东省潮州市区空气质量变化趋势，此方法仅局限于中长期预测 [1] ；程承旗等采用应用时间序列对厦门市PM10浓度分析，指出时间序列预测模型过度突出时间因素在模型中的作用 [2] 。除此之外还有一些模型对于空气质量的使用比较广泛，如多元线性回归模型 [3] 、神经网络预测模型 [4] [5] 等。

本文以对空气质量的识别为背景，收集长沙市2020年1月至2022年12月份空气质量指数(AQI)以及影响空气质量的主要因素的相关数据，运用决策树算法得出影响空气质量的主要因素并且预测长沙空气质量。利用决策树算法所构建的模型对实测数据具有较高的识别预测概率，能够为长沙市空气质量的分析提供参考依据。

2. 数据分析

2.1. 数据来源

分析影响空气质量的因素是做好预测工作的基础，经研究表明，影响空气质量的因素来源于很多方面，国家环保局通过6项主要污染标准：PM2.5浓度(细微颗粒：μg/m³)、PM10浓度(可吸入颗粒物：μg/m³)、SO₂浓度(二氧化硫：μg/m³)、CO浓度(一氧化碳：mg/m³)、NO₂浓度(二氧化氮：μg/m³)、O₃浓度(臭氧：μg/m³)，通过这些污染物浓度的比重来计算空气质量指数(AQI) (Air Quality Index)。

本研究使用的数据为长沙市主城区2020年1月1日至2022年12月31日空气质量国控监测站点的日均浓度数据，每月AQI数据和PM2.5浓度数据由站点根据当天环保总站每小时数据计算求平均的结果，数据来自中国空气质量监测分析平台开放环境数据中心(https://www.aqistudy.cn/)，部分数据见表1。

Table 1. Historical data for air quality index in Changsha from January 2020 to December 2022

表1. 2020年1月至2022年12月份长沙市空气质量指数历史数据

2.2. 数据处理

和其他机器学习分类算法一样，决策树算法需要处理样本数据的离散属性，将样本数据进行离散化处理。参照中国人民共和国国家指标《环境空气质量标准》(GB3095-2012)，将表2的空气质量数据依次分成1、2、3、4、5、6六个等级，分别表示优、良、轻度污染、中度污染、重度污染和严重污染六种情况。参照标准如表2所示：

Table 2. Air quality rating indicators

表2. 空气质量等级指标

3. 研究方法

3.1. k近邻算法

3.1.1. 算法原理

k近邻算法(k-NN算法)由Thomas等人在1967年提出 [6] ，在模式识别中，k近邻算法可以用来对非参数数值进行分类，将训练数据集输入到特征空间中，最终输出的结果为分类标签。其核心思想是：如果一个样本在特征空间中关于k个最相邻的样本，这些样本中出现最多的某一类别，则认为该样本属于这个类别，并具有这个类别上样本的特性。如图1所示，位置圆点在空间范围中有两个类别：三角形和正方形。如果k = 3时，我们选取离圆点最近的三个点，可以看出有两个三角形和一个正方形，因此可以将新样本点划分为三角形类；如果k = 5时，离圆点最近的五个点中，有三个正方形和两个三角形，新样本点就被划分为正方形类，以此类推，当k值有所变化时，新样本点有可能被划分为不同的类别。

3.1.2. 计算流程

k近邻算法进行分类的流程一般如下：

1) 收集样本数据，并按照要求进行分类，以此构建一个已分好类的数据集；

2) 计算测试集与样本数据集中所有数据的欧式距离，见式(1)

$d\left(X,Y\right)=\sqrt{{\displaystyle \underset{k=1}{\overset{n}{\sum }}{\left(X_k-Y_k\right)}^2}}$ (1)

其中， $d\left(X,Y\right)$ 表示X与Y两点之间的距离， $X_k$ 表示点X第k个空间向量的值， $Y_k$ 表示点Y第k个空间向量的值；

3) 根据(2)中计算得出各个点之间距离的大小，进行一个有序排列；

4) 选取与测试集点距离最近的k个点，并分别找出这k个点中每个点所属的类别；

5) 统计前k个样本所在各个类别出现的频率，确定出现频率最高的类别为所求类别 [7] 。

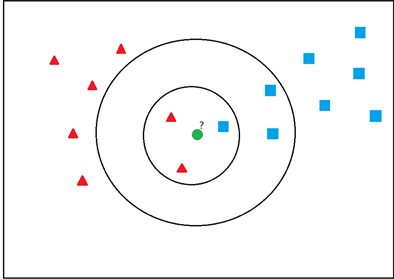
Figure 1. Principle of k-nearest neighbors

图1. k近邻算法原理

3.2. 决策树算法

3.2.1. 算法原理

决策树是用来研究分类问题的一种树状结构模型，通过变量值拆分建立分类规则，按照对类别的影响大小进行树的建立 [8] 。从最开始的AID程序到之后的一些列算法：ID3算法、CART算法、ID4算法、ID5R算法、C4.0算法和C5.0算法，这些算法都是通过建立树状结构进行分类，研究不同特征对某一类别或多个类别的影响效果。其中，CART算法是根据基尼指数分类，既可以用于分类树也可以用作回归树。在分离不同种类时，CART算法采用的是二分递归分割法，将数据不停的分为两种分支，它的分类依据为Gini指数，当Gini指数最小时，确定分割点。由于CART算法在每次用基尼系数进行分类时，只能分为两部分，因此CART算法建立的是二叉树。相比较于其他算法而言，CART算法不仅可以支持剪枝，还可以处理连续性数据。

在分类问题中，假设有k个类别，样本点属于第k类的概率为 $p_k$ ，则概率分布的基尼指数定义为：

$Gini\left(p\right)={\displaystyle \underset{k=1}{\overset{K}{\sum }}{p}_k\left(1-p_k\right)}=1-{\displaystyle \underset{k=1}{\overset{K}{\sum }}{p}_k^2}$ (2)

对于二分类问题，若样本点属于第一个类的概率为p，则概率分布的基尼指数为 $Gini\left(p\right)=2p\left(1-p\right)$ 。如果样本集合D根据特征A是否取某一可能值a被分割为D₁和D₂两部分，即 $D_1=\left\{\left(x,y\right)\in D|A\left(x\right)=a\right\}$ ， $D_2=D-D_1$ ，则在特征A的条件下，集合D的基尼指数定义为

$Gini\left(D,A\right)=\frac{\left|D_1\right|}{\left|D\right|}Gini\left(D_1\right)+\frac{\left|D{}_2\right|}{\left|D\right|}Gini\left(D_2\right)$ (3)

基尼指数 $Gini\left(D\right)$ 表示集合D的不确定性，基尼系数 $Gini\left(D,A\right)$ 表示经 $A=a$ 分割后集合D的不确定性。基尼指数值越大，样本集合的不确定性也就越大。

3.2.2. 计算流程

根据训练数据集，从根节点开始，递归地对每个节点进行如下操作，构建二叉决策树 [9] 。

1) 首先计算gini系数，挑选gini系数值最大的特征作为最优特征。对于给定的训练数据集D，计算现有特征对该数据集的基尼系数。此时，对每一个特征A，对其每个可能取的值a，根据样本点对 $A=a$ 的测试为“是”或“否”将D分割为D₁和D₂两部分，利用式(3)计算 $A=a$ 时的基尼系数。

2) 对所有可能的特征A以及它们所有可能的切分点a中，选择基尼指数最小的特征及其对应的切分点作为最优特征与最有切分点。依最优特征与最优切分点，从现结点生成两个子结点，将训练数据集依特征分配到两个子结点中去。

3) 对两个子结点递归的调用(1)、(2)，直至满足停止条件。

4) 生成CART决策树。

4. 模型构建

本文构建模型包含训练数据集所有样本的n维空间，其中n为样本特征数，本文构建该模型即把空气质量数据集中1096个样本根据其特征值输入特征空间中。将空气质量数据集分为训练集和测试集两部分，分别为80%和20%，样本个数分别为876和220。其中，训练集用来构建模型，测试集用来测试模型的拟合优度。

对于k近邻算法模型中k值分别以1、3、5、7、9、11进行选取，针对k的每个取值构建模型，得到k近邻模型个数为6，计算每个模型的预测准确率，本研究利用python的sklearn机器学习库来训练模型，通过不同的k值，得出测试集的准确率，选择准确率最高的模型作为本研究的空气质量预测评估模型。

对于决策树模型，在数据集完成采集后调用Skearn中的DecisionTreeClassifier()函数，随机种子random_state = 0，设置参数max_depth，criterion，使用GridSearchCV查找最优参数，见表3决策树参数。

Table 3. Decision tree parameters

表3. 决策树参数

5. 评估标准

5.1. 准确率

准确率是分类正确的样本数与所有样本数的比值，它是最常见、最容易理解的指标。通常来讲准确率越高，分类器的性能也越好，其中准确率表达式为：

$Accuracy=\frac{m^{\prime }}{m}$ (4)

其中Accuracy表示准确率，m'为测试集被正确分类的样本，m为测试集总样本。

5.2. 混淆矩阵

由于准确率只能评估模型的全局准确程度，样本数量不平衡时，其预测结果可能失效；而且对于多分类问题而言，每一类样本的识别准确率都应当被考虑，因此就有了混淆矩阵的出现 [10] 。

本文使用TP (True Positive)、FP (False Positive)、FN (False Negative)和TN (True Negative)作为评价指标。如表4混淆矩阵表所示，TP为正样本被预测为正类的概率，FN为正样本被预测为负样本的概率，FP为负样本被预测为正样本的概率，TN为负样本被预测为负类的概率。

Table 4. Confusion matrix table

表4. 混淆矩阵表

6. 结果分析

6.1. 模型建立与精度分析

为了更加直观地看出两种算法对于空气质量数据的预测表现，对测试集上的预测结果进行可视化，绘制混淆矩阵，结果如图2所示，其最终横纵坐标的0~5代表空气质量等级指标。通过混淆矩阵可以计算这两种算法对于空气质量等级的预测情况如表5所示。

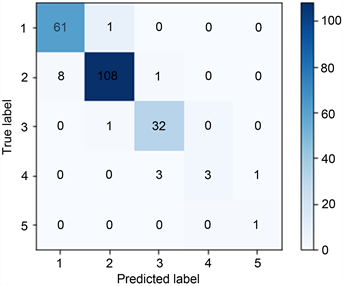
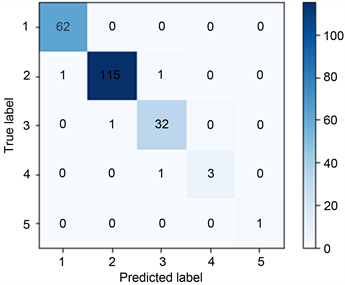(a) k近邻算法 (b) 决策树算法

Figure 2. Confusion matrix of prediction results of two algorithms

图2. 两种算法预测结果混淆矩阵

Table 5. Prediction of each grade

表5. 各等级预测情况

通过检验标准对这两种算法进行比较分析可得，决策树模型相对于k近邻算法模型，结果预测精度更高，因此最终选择决策树算法进行预测。分析的结果与真实值基本一致，说明决策树模型可以较好地用于空气质量的分析预测。

6.2. 影响因素相关性分析

为了充分验证模型的精度，进一步分析大气污染状况及其污染主要因素，利用决策树模型生成决策树，部分决策树如图3所示。

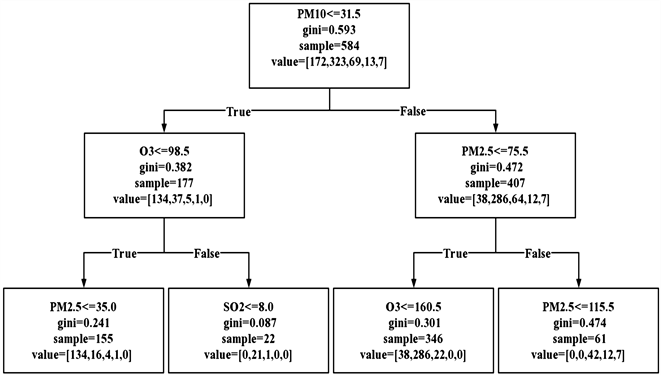
Figure 3. Air quality decision tree diagram

图3. 空气质量决策树图

图中gini = ？代表基尼指数的大小，sample = ？表示在划分之前有多少个样本，value = [?, ?, ?]表示样本标签中有多少个类别，每个类别的样本数。决策树中出现比较重要的指标有5个，按照其划分的重要程度依次是：PM10、PM2.5、O₃、SO₂、CO。

7. 结论

针对空气质量分析预测问题，本研究考虑了空气污染物与空气质量的关系，对历史数据集进行分析及处理，以长沙市区为研究对象，建立了基于决策树算法的空气质量指数(AQI)预测模型，并选择k近邻算法模型作为对比模型，结果与真实值基本一致。这说明所建的模型合理可靠，能够为预测长沙市空气质量提供参考依据。但是，供模型学习使用的数据集不够充分，格式也不够规范，这两个因素共同导致了本文模型预测不能达到完全正确，甚至一些预测结果准确率比较低。模型中选择的决策树算法如何针对不同模板数据集搜索一个最优深度，这些仍需要进一步研究。

通过上述分析可知，影响空气质量的主要因素有五项，其中颗粒物污染PM10的比重较大，SO₂所代表的固定源排放比较低。今后应采取增加地面植被尤其是常绿植物的覆盖率，相关部门应加强执法，严格按照环境保护的要求和法规执法，控制污染物排放量，有效制止环境污染问题。通过报纸、互联网、多媒体等各种形式，加大环境保护宣传力度，提高人们的环保意识。提倡使用风能、太阳能等环保资源，尽量减少私家车的使用，选择乘坐公共交通工具。

基金项目

长沙理工大学研究生科研创新项目(CLSJCX22148)资助。