基于高频数据的PGARCH模型的拟极大指数似然估计

Quasi Maximum Exponential Likelihood Estimator of PGARCH Model Based on High Frequency Data

摘要: 作为GARCH族模型的重要拓展模型之一，PGARCH模型的估计往往采用基于日度数据的拟极大似然估计方法。为了探究高频信息对PGARCH模型估计的影响，基于Visser (2011)的研究，本文使用波动率代表模型来整合高频数据，并使用拟极大指数似然估计方法(QMELE)对PGARCH模型进行估计，同时探究了拟极大指数似然估计的渐近性质和模型估计效率的评判标准。模拟研究和实证分析证实，基于高频数据的拟极大指数似然估计有效地提升了PGARCH模型的参数估计精度，这说明基于高频数据的拟极大似然指数估计具有一定的应用价值。

Abstract: As one of the important extended models of the GARCH family model, it is more common to use quasi maximum likelihood estimator to fit PGARCH model with daily data. Referring to Visser (2011), this article applies volatility representative models to integrate high-frequency data, and then uses the quasi maximum exponential likelihood estimator (QMELE) to fit the PGARCH model, so that we can explore the impact of high-frequency information on the estimation of the PGARCH model. Meanwhile, we establish the asymptotic properties of QMELE and the evaluation criteria for model estimation efficiency. Simulation research and empirical analysis have confirmed that QMELE with high-frequency data effectively improves the parameter estimation accuracy of the PGARCH model, which indicates that the QMELE based on high-frequency data has a certain application value.

1. 引言

波动率是描述了金融资产的收益率在特定时期内偏离均值的参数，可用来衡量金融资产收益的不确定性，反应了金融资产的风险水平。Engel (1982)提出的自回归条件异方差(ARCH)模型和Bollerslev(1986)推广的广义自回归条件方差(GARCH)模型是刻画波动率的聚集性和时变性的经典模型 [1] [2] 。ARCH模型和GARCH模型中的方差函数的幂次项是平方的形式，但是Engle (1982)在提出ARCH模型的时候就指出，ARCH模型中方差函数的二次幂的设定未必是最优的形式，为此他提出了ARCH模型的绝对值形式。延续这种ARCH模型或GARCH模型的方差函数幂的变换方式，衍生了一系列GARCH模型的拓展模型——PGARCH类模型。例如，Higgins (1992)提出了非线性ARCH模型，Ding (1993)提出了APARCH模型，Diebolt和Guégan (1994)提出了beta-ARCH模型和beta-GARCH模型，Hwang和Kim (2004)提出了Box-Cox PGARCH(1,1)模型(门限PGARCH(1,1)模型)，Pan (2008)提出了Box-Cox PGARCH(p,q)模型(门限PGARCH(p,q)模型) [3] [4] [5] [6] [7] 。本文将上述ARCH模型或者GARCH模型的方差函数的幂项参数化的模型统称为PGARCH类模型。上述研究表明，GARCH类模型的方差函数可以有不同的形式，PGARCH类模型将方差函数幂项参数化不仅能刻画金融数据的聚集性，而且更能考虑到异常值的情况 [8] 。出于简洁性的考量，本文研究的模型为PGARCH(1,1)，具体的模型结构如下：

$r_n={\sigma }_n{z}_n,$ (1)

${\sigma }_n^{2\delta }=\omega +\alpha r_{n-1}^{2\delta }+\beta {\sigma }_{n-1}^{2\delta },$ (2)

其中，待估参数 $\delta >0$ ， $\omega >0$ ， $\alpha >0$ ， $\beta >0$ 。 $r_n$ 表示某标的资产第n天的日收益率。 ${\sigma }_n$ 表示第n天的波动率。 $\left\{z_n\right\}$ 是一组期望为0、方差为1的独立同分布的随机序列，且 $z_n$ 独立于 ${\sigma }_s\left(s<n\right)$ 。当 $\delta =1$ 时，PGARCH(1,1)模型则退化为传统的GARCH(1,1)模型。PGARCH模型是GARCH模型的简单变形，它将GARCH模型的方差函数的幂次项设为一个待估参数，这种设置为PGARCH模型的估计增加了难度。作为GARCH模型的拓展，PGARCH模型其亦适用于资产波动性的分析和预测，对投资者的金融决策具有借鉴意义。

随着互联网技术的快速发展，高频数据的爆发式增长为波动率建模提供了更多的数据支持。如何使用囊括了更多的价格波动信息的高频数据来提高低频模型的参数估计成为了热门课题。Visser (2011)利用高频数据来研究了GARCH模型的拟极大似然估计(QMLE)：Visser (2011)通过构造波动率代表来对高频数据进行加工，从而把高频信息整合到日频GARCH模型中，接着对模型采取拟极大似然估计(QMLE)，并在实证中得到了参数估计精度有所提升的结论 [9] 。这为如何使用高频数据来提高模型拟合效果提供了新途径。参考Visser (2011)的研究，黄金山(2014)研究了GARCH模型的拟极大指数似然估计，证实高频数据的使用提高了模型估计效率 [10] 。Huang (2015)参考Visser (2011)使用高频数据对GJR-GARCH模型进行M估计 [11] 。Fan (2017)基于日内高频数据研究了周期GARCH模型的季节性波动和建模过程 [12] 。吴思鑫(2018)对非平稳的GARCH模型进行拟极大指数似然估计，并从平均绝对误差的角度得出QMELE优于QMLE的结论 [13] 。

另一方面，Visser (2011)对GARCH模型进行估计时使用了拟极大似然估计(QMLE) [1] 。拟极大似然估计(QMLE)假设了模型的误差项 $\left\{z_n\right\}$ 的四阶矩存在，然而尖峰厚尾的金融数据使得四阶矩的条件不总是成立，因此QMLE不总是得到令人满意的结果。为了解决这个问题，一种可行的方法是使用拟极大指数似然估计(QMELE)替代拟极大似然估计方法。拟极大指数似然估计(QMELE)只需要模型的误差项 $\left\{z_n\right\}$ 的二阶矩存在，相较QMLE来说QMELE条件更宽泛，QMELE也更稳健。张兴发(2016)研究了一类特殊的GARCH-M模型的拟极大指数似然估计(QMELE)的局部参数估计，并给出了在较弱的矩条件下的QMELE的渐近正态性证明 [14] 。张童巍(2021)通过拟极大指数似然估计(QMELE)方法对GARCH-M模型和DTGARCH模型进行建模 [15] 。

尽管使用高频数据对GARCH族模型建模成为常态，但是目前尚未有高频数据与PGARCH模型估计结合的相关研究。于是本文在GARCH模型对幂项参数化这一模型变换规律的背景下归纳提出了PGARCH模型，然后参考Visser (2011)的研究使用了日内高频数据对PGARCH模型进行估计，估计方法是拟极大指数似然估计，接着探究了QMELE估计的渐近性质和模型估计效果好坏的判定准则。本文的文章结构如下：第1节绪论，概况了本文的学术背景和研究意义，梳理了文章的脉络和思路；第2节介绍了本文研究的PGARCH模型、日内尺度模型和波动率代表模型，给出QMELE估计方法的理论准备；第3节研究了基于高频数据的PGARCH模型的QMELE估计及给出了QMELE的渐近性质；第4节和第5节分别从模拟研究和实证分析的角度阐述QMELE估计方法的实用性；第6节是对文章的主要研究成果的总结。

2. PGARCH模型与高频信息

2.1. 尺度模型

PGARCH模型(1)~(2)是一个由日间收益率刻画的日频的离散随机模型。为了引入高频数据，需要引入日内连续的收益过程 $R_n\left(u\right)$ 。参考Visser (2011)，将每天的交易时间单位化到区间[0, 1]上，u记为交易时间的记号，那么 $u\in \left[0,1\right]$ 。根据记录下交易日内连续的交易价格变动情况，得到的 $R_n\left(u\right)$ 为日内连续的收益过程，从而构造的尺度模型：

$R_n\left(u\right)={\sigma }_n{Z}_n\left(u\right),0\le u\le 1,$ (3)

${\sigma }_n^{2\delta }=\omega +\alpha r_{n-1}^{2\delta }+\beta {\sigma }_{n-1}^{2\delta },$ (4)

其中， $R_n\left(u\right)$ 表示某资产第n天的日内收益率， $Z_n\left(u\right)$ 是一组期望为0、方差为1的独立同分布的随机序列，且 $Z_n\left(u\right)$ 独立于 ${\sigma }_s\left(s<n\right)$ 。对于日内的收益过程来说，当天的波动率 ${\sigma }_n$ 是个常数。当可以看出，整合了高频信息的尺度模型(3)~(4)包含了日频PGARCH模型(1)~(2)作为一个特例。当 $u=1$ ， $R_n\left(1\right)=r_n$ ， $Z_n\left(1\right)=z_n$ ，尺度模型(3)~(4)即转化为了日频模型(1)~(2)。由于QMELE对PGARCH模型的矩条件要求其一阶矩存在，因此需要假设日频的PGARCH模型(1)~(2)的残差项 $E\left|z_n\right|=1$ 。那么为保持模型的一致性，日内尺度模型亦需要假设 $E\left|Z_n\left(1\right)\right|=1$ 。

2.2. 波动率代表模型

尽管尺度模型(3)~(4)的建立把日频的PGARCH模型和日内高频数据联系了起来，模型(3)~(4)还是无法直接估计参数，因此需要进一步加工日内高频数据。参考Visser (2011)，本节引入波动率代表。波动率代表是关于日内高频数据非负的一元函数，它通过对日内的高频数据进行加工得到的统计量，常见的波动率代表有已实现波动率，日内价格极差和日收益率的绝对值等。一般来说，波动率代表是非负的且满足正齐性：对于任意的非零常数 $\alpha$ 和日内收益率 $R_n\left(u\right)$ 满足：

$H\left(\alpha R_n\right)=\alpha H\left(R_n\right),\alpha >0.$ (5)

本文使用的波动率代表包括常见的已实现波动率和日收益率的绝对值，其中已实现波动率是已实现方差的平方根，日收益率的绝对值由波动率代表的定义知也是一个特殊的波动率代表。

那么由波动率代表的正齐性及模型(3)得

$H_n=H\left(R_n\left(u\right)\right)=H\left({\sigma }_n{Z}_n\left(u\right)\right)={\sigma }_{n}H\left(Z_n\left(u\right)\right).$ (6)

设 $\mu =E\left|H\left(Z_n\left(u\right)\right)\right|$ ，令 ${\sigma }_n^{*}={\sigma }_n\mu$ ， $Z_n^{*}=H\left(Z_n\left(u\right)\right)/\mu$ 。那么将其带入(6)式得

$H_n={\sigma }_{n}H\left(Z_n\left(u\right)\right)={\sigma }_n\cdot \mu \frac{H\left(Z_n\left(u\right)\right)}{\mu }={\sigma }_n^{*}{Z}_n^{*}.$ (7)

那么整合了高频信息的波动率代表模型可以写为：

$H_n={\sigma }_n^{*}{Z}_n^{*},$ (8)

${\sigma }_n^{*}{}^{2{\delta }^{*}}={\omega }^{*}+{\alpha }^{*}{r}_{n-1}^{2{\delta }^{*}}+{\beta }^{*}{\sigma }_{n-1}^{*2{\delta }^{*}},$ (9)

其中， $\mu >0$ ， $Z_n^{*}$ 是经过标准化的独立同分布的随机序列，满足 $E\left|Z_n^{*}\right|=1$ ，且 $Z_n^{*}$ 独立于 ${\sigma }_s^{*}\left(s<n\right)$ 。比较模型(1)~(2)和模型(8)~(9)，可以发现二者有着相似的结构形式。前者恰好是后者的一个特例，当 $H_n=\left|r_n\right|$ 时， $\mu =1$ ， $z_n=Z_n^{*}$ ， ${\sigma }_n={\sigma }_n^{*}$ ，此时模型(8)~(9)可以写成模型(1)~(2)的形式。前者的待估参数为 $\theta ={\left(\delta ,\omega ,\alpha ,\beta \right)}^{\prime }$ 后者的待估参数为 ${\theta }^{*}={\left({\delta }^{*},{\omega }^{*},{\alpha }^{*},{\beta }^{*}\right)}^{\prime }$ ，二者之间有以下的数量关系：

${\omega }^{*}=\omega {\mu }^{2\delta },{\alpha }^{*}=\alpha {\mu }^{2\delta },{\beta }^{*}=\beta ,{\delta }^{*}=\delta .$ (10)

在对PGARCH模型进行QMELE估计时，先对模型(8)~(9)进行估计得到待估参数 ${\hat{\theta }}^{*}$ ，再利用(10)的等式关系即可得到日频的PGARCH模型的待估参数 $\hat{\theta }$ 。

3. 参数估计

3.1. 拟极大指数似然估计

已知模型(1)~(2)的参数向量 $\theta ={\left(\delta ,\omega ,\alpha ,\beta \right)}^{\prime }\in \Theta$ ，假定参数真值 ${\theta }_0^{*}={\left({\delta }_0^{*},{\omega }_0^{*},{\alpha }_0^{*},{\beta }_0^{*}\right)}^{\prime }$ 是参数空间 $\Theta$ 的一个内点。记 $F_n$ 是由 $\left\{R_n,R_{n-1},R_{n-2},\cdots \right\}$ 生成的前n期的信息集。那么 $E\left(H_n|F_{n-1}\right)={\sigma }_n^{*}$ 。在给出基于拉普拉斯分别的拟极大似然估计前，先引入辅助变量 $x_n$ 。记 ${\phi }_n$ 是由 $\left\{-1,1\right\}$ 组成的独立同分布的随机变量。 ${\phi }_n$ 与模型(8)~(9)独立，且 $P\left({\phi }_n=1\right)=P\left({\phi }_n=1\right)=1/2$ 。令 $x_n={\phi }_n{H}_n$ ，那么 $E\left(x_n|F_{n-1}\right)=0$ ， $E\left(\left|x_n\right||F_{n-1}\right)={\sigma }_n^{*}$ 。基于可观测的值 ${\left\{r_n\right\}}_{n=1}^N$ ，未知参数 $\theta$ 的待估参数 ${\theta }^{*}$ 的拟对数似然函数和QMELE估计量为：

$\begin{array}{c}{L}_n\left({\theta }^{*};x_1,x_2,x_3,\cdots \right)={\displaystyle \underset{n=1}{\overset{N}{\sum }}-\left[\log \left({\sigma }_n^{*}\left({\theta }^{*}\right)+\frac{\left|x_n\right|}{{\sigma }_n^{*}\left({\theta }^{*}\right)}\right)\right]}\\ ={\displaystyle \underset{n=1}{\overset{N}{\sum }}-\left[\log \left({\sigma }_n^{*}\left({\theta }^{*}\right)+\frac{\left|H_n\right|}{{\sigma }_n^{*}\left({\theta }^{*}\right)}\right)\right]},\end{array}$ (11)

${\hat{\theta }}^{*}=\arg \max L_n\left({\theta }^{*}\right).$ (12)

为了证明 ${\theta }^{*}$ 的QMELE估计具有一致性和渐近正态性，需要作出以下基本假设：

1) $Z_n^{*}$ 服从非退化的对称分布，且存在某些 $\Delta >0$ ，使得 $E{\left|Z_n\right|}^{\Delta }<+\infty$ 和对于任何的 $\mu >0$ 有 $\underset{n\to o}{\lim }{n}^{-\mu }P\left\{Z_n^{*}{}^2\le n\right\}$ 。

2) 参数空间 $\Theta$ 是 $R^4$ 上的紧凑子集， ${\theta }^{*}$ 是 $\Theta$ 的内点。对于所有的 ${\theta }^{*}\in \Theta$ ，都有李雅普诺夫指数 $\gamma \left({\theta }^{*}\right)<0$ 。

3) $E\left(Z_n^{*}{}^2\right)=1$ ，且 $E{Z}_n^{*}{}^4<\infty$ 。

参考黄金山和陈敏(2014)的类似证明可得 ${\hat{\theta }}^{*}$ 的渐进分布 [10] ：

$\sqrt{N}\left({\hat{\theta }}_0^{*}-{\theta }_0^{*}\right)\stackrel{d}{\to }N\left(0,{\Sigma }^{*}\right),N\to \infty ,$ (13)

${\Sigma }^{*}=4\left(E\left(Z_n^{*}{}^2\right)-1\right)G{\left({\theta }^{*}\right)}^{-1},$ (14)

$G{\left({\theta }_0^{*}\right)}_{i,j}=E\left[\frac{1}{{\sigma }_n^4\left({\theta }_0^{*}\right)}\frac{\partial {\sigma }_n^2\left({\theta }_0^{*}\right)}{\partial {\theta }_i^{*}}\frac{\partial {\sigma }_n^2\left({\theta }_0^{*}\right)}{\partial {\theta }_j^{*}}\right].$ (15)

那么计算G中需要用到的 ${\sigma }_n^{*}{}^2$ 对各个参数的偏导如下：

${\sigma }_n^{*}{}^{2{\delta }^{*}}={\omega }^{*}+{\alpha }^{*}{r}_{n-1}^{2{\delta }^{*}}+{\beta }^{*}{\sigma }_{n-1}^{*2{\delta }^{*}}=\frac{{\omega }^{*}}{1-{\beta }^{*}}+{\alpha }^{*}{\displaystyle \underset{i=1}{\overset{\infty }{\sum }}{\beta }^{*}{}^{i-1}}{r}_{n-i}^{2{\delta }^{*}},$ (16)

$\frac{\partial {\sigma }_n^{*}{}^2}{\partial {\delta }^{*}}={\text{e}}^{\frac{\ln C_n}{{\delta }^{*}}}\left[-\frac{\ln C_n}{{\delta }^{*}{}^2}+\frac{k_n}{{\delta }^{*}{C}_n}\right],\frac{\partial {\sigma }_n^{*}{}^2}{\partial {\omega }^{*}}=\frac{C_n^{\frac{1}{{\delta }^{*}}-1}}{{\delta }^{*}\left(1-{\beta }^{*}\right)},$ (17)

$\frac{\partial {\sigma }_n^{*}{}^2}{\partial {\alpha }^{*}}=\frac{C_n^{\frac{1}{{\delta }^{*}}-1}\left({\displaystyle \underset{i=1}{\overset{\infty }{\sum }}{\beta }^{*}{}^{i-1}}{r}_{n-i}^{2{\delta }^{*}}\right)}{{\delta }^{*}},$ (18)

$\frac{\partial {\sigma }_n^{*}{}^2}{\partial {\beta }^{*}}=\frac{C_n^{\frac{1}{{\delta }^{*}}-1}\left[{\displaystyle \underset{i=1}{\overset{\infty }{\sum }}\left(i-1\right){\beta }^{*}{}^{i-2}{r}_{n-i}^{2{\delta }^{*}}}+\frac{{\omega }^{*}}{{\left(1-{\beta }^{*}\right)}^2}\right]}{{\delta }^{*}}.$ (19)

在上述式子中， $C_n=\frac{{\omega }^{*}}{1-{\beta }^{*}}+{\alpha }^{*}{\displaystyle \underset{i=1}{\overset{\infty }{\sum }}{\beta }^{*}{}^{i-1}{r}_{n-i}^{2{\delta }^{*}}}$ ， $k_n={\alpha }^{*}{\displaystyle \underset{i=1}{\overset{\infty }{\sum }}{\beta }^{*}{}^{i-1}{r}_{n-i}^{2{\delta }^{*}}}\ln r_{n-i}^2$ 。

记参数 ${\hat{\theta }}^{*}={\left({\hat{\delta }}^{*},{\hat{\omega }}^{*},{\hat{\alpha }}^{*},{\hat{\beta }}^{*}\right)}^{\prime }$ 的渐近方差为 ${\left({\sigma }_{\delta }^{*}{}^2,{\sigma }_{\omega }^{*}{}^2,{\sigma }_{\alpha }^{*}{}^2,{\sigma }_{\beta }^{*}{}^2\right)}^{\prime }$ ，那么模型(3)~(4)的参数 $\hat{\theta }={\left(\hat{\delta },\hat{\omega },\hat{\alpha },\hat{\beta }\right)}^{\prime }$ 的渐近分布分别为：

$\sqrt{N}\left(\hat{\delta }-{\delta }_0\right)\stackrel{L}{\to }\left(0,{\sigma }_{\delta }^{*}{}^2\right),$ (20)

$\sqrt{N}\left(\hat{\omega }-{\omega }_0\right)\stackrel{L}{\to }\left(0,\frac{{\sigma }_{\omega }^{*}{}^2}{{\mu }^{4\delta }}\right),$ (21)

$\sqrt{N}\left(\hat{\alpha }-{\alpha }_0\right)\stackrel{L}{\to }\left(0,\frac{{\sigma }_{\alpha }^{*}{}^2}{{\mu }^{4\delta }}\right),$ (22)

$\sqrt{N}\left(\hat{\beta }-{\beta }_0\right)\stackrel{L}{\to }\left(0,{\sigma }_{\beta }^{*}{}^2\right).$ (23)

3.2. 日频参数的估计

由QMELE方法估计得到PGARCH模型参数的估计值 ${\hat{\theta }}^{*}={\left({\hat{\delta }}^{*},{\hat{\omega }}^{*},{\hat{\alpha }}^{*},{\hat{\beta }}^{*}\right)}^{\prime }$ ，结合公式(10)，即可得到 $\theta$ 的一个估计。由于 $$ ，可将 ${\delta }^{*}$ 视为一个常数来对 $\mu$ 进行估计。由等式 ${\sigma }_n^{*}={\sigma }_n\mu$ ，可得 $\mu$ 的一个估计量：

$\tilde{\mu }=\frac{1}{N}{\displaystyle \underset{n=1}{\overset{N}{\sum }}{\tilde{\sigma }}_n^{*}/{\tilde{\sigma }}_n},$ (24)

其中 ${\tilde{\sigma }}_n^{*}$ 表示经高频数据估算得到的波动率， ${\tilde{\sigma }}_n$ 表示经 $H_n=\left|r_n\right|$ 估计得到的波动率。那么PGARCH模型(1)~(2)的参数为：

$\hat{\delta }={\hat{\delta }}^{*},\hat{\omega }={\hat{\omega }}^{*}/{\mu }^{2\delta },\hat{\alpha }={\hat{\alpha }}^{*}/{\mu }^{2\delta },\hat{\beta }={\hat{\beta }}^{*}.$ (25)

由3.1的研究可知，模型的估计效率由残差项 $Z_n^{*}{}^2$ 决定：当 $E\left(Z_n^{*}{}^2\right)$ 越小，参数估计的方差 ${\Sigma }^{*}$ 也越小，估计就越有效。因此我们可以通过比较 $E\left(Z_n^{*}{}^2\right)$ 的大小来判断基于不同的波动率代表的估计精度。通过推导，可以发现 $E\left(Z_n^{*}{}^2\right)$ 大小与MH值的大小成正比关系：

$E\left(Z_n^{*}{}^2\right)=E{\left(\frac{H\left(Z_n\left(u\right)\right)}{\mu }\right)}^2=E{\left\{\frac{H\left(Z_n\left(u\right)\right)}{E\left|H\left(Z_n\left(u\right)\right)\right|}\right\}}^2=\frac{E{\left[H\left(Z_n\left(u\right)\right)\right]}^2}{{\left[E\left|H\left(Z_n\left(u\right)\right)\right|\right]}^2}.$ (26)

考虑到 ${\sigma }_n$ 和 $Z_n$ 的独立性， $H_n$ 是非负的，则有：

$E\left(H_n\right)=E\left({\sigma }_{n}H\left(Z_n\left(u\right)\right)\right)=E\left({\sigma }_n\right)E\left[H\left(Z_n\left(u\right)\right)\right]=E\left({\sigma }_n\right)E\left|H\left(Z_n\left(u\right)\right)\right|.$ (27)

令 $c=E\left({\sigma }_n^2\right)/{\left[E\left({\sigma }_n\right)\right]}^2$ ，显然c是一个大于0的常数。当我们通过乘以常数c来变换方差方程(26)时，我们可以导出如下统计量：

$E\left(Z_n^{*}{}^2\right)\cdot c=\frac{E{\left[H\left(Z_n\left(u\right)\right)\right]}^2}{{\left[E\left|H\left(Z_n\left(u\right)\right)\right|\right]}^2}\cdot \frac{E\left({\sigma }_n^2\right)}{{\left[E\left({\sigma }_n\right)\right]}^2}=\frac{E\left(H_n^2\right)}{{\left[E\left(H_n\right)\right]}^2}.$ (28)

显然(26)式和(28)式成正比关系，将(28)式定义为新的统计量MH：

$\text{MH}=\frac{E\left(H_n^2\right)}{{\left[E\left(H_n\right)\right]}^2}.$ (29)

此时寻找参数的渐进方差最小的问题就转换为最小的统计量MH问题。当MH值越小，方差越小，估计精度越高，估计越有效。

4. 模拟研究

本节通过数值模拟来检验QMELE的实用性：对建立起的PGARCH模型采用QMELE方法估计，然后从估计参数结果的偏差、标准差和MH均值的角度来评价估计效果。上述实验的重复1000次。为了达到模拟的效果，首先需要建立日内的标准化随机过程 $Z_n\left(u\right)$ ，这里使用平稳的Ornstein-Uhlenbeck过程建模：

$\text{d}{\Gamma }_n\left(u\right)=-\phi \left({\Gamma }_n\left(u\right)-u_{\Gamma }\right)\text{d}u+{\sigma }_{\Gamma }\text{d}{B}_n^{\left(2\right)}\left(u\right),$ (30)

$\text{d}{\Psi }_n\left(u\right)=\exp \left({\Gamma }_n\left(u\right)\right)\text{d}{B}_n^{\left(1\right)}\left(u\right),u\in \left[0,1\right],$ (31)

$m=E\left|{\Psi }_n\left(1\right)\right|,Z_n\left(u\right)={\Psi }_n\left(u\right)/m.$ (32)

其中， $\phi =1/2$ ， ${\sigma }_{\Gamma }=1/4$ ， ${\mu }_{\Gamma }=-1/16$ 。两个布朗运动 $B_n^{\left(1\right)}$ 和 $B_n^{\left(2\right)}$ 是不相关的。 $Z_n\left(0\right)=0$ ， ${\Gamma }_n\left(0\right)$ 从平稳分布 $N\left({\mu }_{\Gamma },{\sigma }_{\Gamma }^2\right)$ 中随机产生。 $u\in \left[0,1\right]$ ，日内的交易时间[0, 1]被划分为240个等份区间，每个等分区间对应交易日的1分钟频率的交易数据，每五个等分区间对应交易日的五分钟频率的交易数据。以此类推，得到离散化的日内标准过程 $Z_n\left(u\right)$ 。式子(32)使得模型满足 $E\left|Z_n\left(u\right)\right|=1$ 。模拟实验中模型(3)~(4)中的参数真值 ${\theta }_{\text{0}}$ 设为： ${\left(\text{0}\text{.8},0.2,0.3,0.55\right)}^{\prime }$ 。

本节选择了频率为5分钟、10分钟、15分钟、30分钟的已实现波动率和日收益率的波动率代表，分别记为RV5，RV10，RV15，RV30， $\left|r_n\right|$ 。如果不特指哪种波动率代表，本文中用到高频数据的波动率代表则使用RV表示。比如，10分钟频率的高频数据算得的已实现波动率的计算方式如下：

$H_n=\text{RV}{10}_n={\left[{\displaystyle \underset{i=1}{\overset{24}{\sum }}\left(R_n\left(u_{i\ast 10}\right)-R_n\left(u_{\left(i-1\right)\ast 10}\right)\right)}\right]}^{\frac{1}{2}},$ (33)

其中，设置初值 $R_n\left(0\right)=0$ ， ${\left\{R_n\left(u_i\right)\right\}}_{i=1}^{240}$ 表示生成的日内收益率序列。为了与基于高频数据的估计做对比，这里使用了波动率代表 $H_n=\left|r_n\right|$ ，此时表示使用日频数据对模型进行估计。

在一次模拟中，样本量分别设置为500，1000和1500天。实验重复1000次。对于选定的波动率代表，一次模拟中MH的估计值如下：

$\widehat{\text{MH}}=\left(\frac{1}{N}{\displaystyle \underset{n=1}{\overset{N}{\sum }}{H}_n^2}\right)/{\left(\frac{1}{N}{\displaystyle \underset{n=1}{\overset{N}{\sum }}{H}_n}\right)}^2=N{\displaystyle \underset{n=1}{\overset{N}{\sum }}{H}_n^2}/{\left({\displaystyle \underset{n=1}{\overset{N}{\sum }}{H}_n}\right)}^2.$ (34)

模拟的结果如表1所示。表1给出基于QMELE估计的偏差、标准差、MH均值，其中Mean.MH是1000次重复实验中MH值的平均数，用于判断参数估计效率。

从表1可以看出，所有参数估计的偏差和标准差都随着样本量的增加而逐渐变小，这符合一致估计的特性。在相同样本量下，与 $\left|r_n\right|$ 相比，通过高频数据的波动率代表RV估计得到的参数偏差和标准差明显变小。这说明基于高频数据的波动率代表的估计优异于基于 $\left|r_n\right|$ 的估计。另一方面，如果比较基于高频数据的已实现波动率的估计标准差，那么可以发现随着抽样频率的增加，估计的标准差越小。这说明了基于QMELE估计，更高频的信息的引入带来了更精准的估计结果，侧面说明了基于QMELE的估计波动率代表模型能够更有效地诠释了高频数据携带的金融市场信息，进而更好地刻画PGARCH模型。比较不同的Mean.MH值，RV的Mean.MH值都比 $\left|r_n\right|$ 的小，该角度也证明了基于高频信息的参数估计效率有所提高。表1中样本量N = 500时，Mean.MH最小值出现在RV5的情况下，这说明此时的估计最有效。表1中样本量N = 1000时，Mean.MH最小值出现在RV5的情况下，这说明此时的估计最有效。样本量N = 1500时，得到同样的结果。参数的估计标准差最小时，与之对应的Mean.MH值也最小，说明上一节讨论的最优波动率代表评判标准是合理的。综上所述，基于高频信息的已实现波动率(RV)比基于日频信息的 $\left|r_n\right|$ 的估计效果好，基于高频数据的QMELE能有效地刻画PGARCH模型，高频数据的使用使得PGARCH模型的估计精度有所提高。

Table 1. Bias, standard deviation, average of MH based on QMELE

表1. 基于QMELE估计的偏差、标准差、MH均值

5. 实证分析

在本节中，将上述QMELE方法应用到实例上，使用的数据源是从2016年6月28日到2020年8月4日的上证指数(000001)。该数据集包含1000个交易日的5分钟间隔的收盘价格信息，每天的观测值总共48个。记上证指数第n天的日内收益价格为 $P_n\left(u\right)$ ，其中 $n=1,2,\cdots ,N$ ， $u\in \left[0,1\right]$ 。当 $u=1$ 时， $P_n\left(1\right)$ 表示第n天的收盘价格。那么日内收益率的计算方式如下：

$R_n\left(u\right)=\left[\log P_n\left(u\right)-\log P_{n-1}\left(u\right)\right]\times 100.$ (35)

图1给出了上证指数的每日收盘价格时序图、日收益率和5分钟收益序列图，时间跨度是1000个交易日。其中图1(a)图刻画了上证指数的每日收盘价格走势，图1(b)图刻画了交易日的日收益率的走势，图1(c)图刻画了交易日内的平均的5分钟收益率的走势。可以看出，图1(a)~(c)三幅图的波峰和波谷出现的位置接近；图1(b)，图1(c)图中显示上证指数的日收益率和5分钟收益率存在聚集性，大的波动率往往紧接着大的波动率，图中显示为平稳序列。

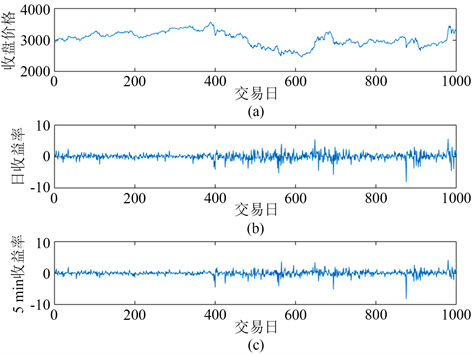
Figure 1. Sequence diagram of daily closing price, daily yield, and 5-minute yield of the Shanghai Composite Index over 1000 trading days

图1. 1000个交易日的上证指数的日收盘价格、日收益率合5分钟收益率的序列图

进行参数估计时，本节采用了频率为5分钟、10分钟、15分钟、30分钟的波动率代表和日收益率的波动率代表。图2分别是基于日收益率、5分钟收益率、15分钟收益率和30分钟收益率的波动率代表时序图。可以看出基于高频数据计算的波动率代表走向相似，且与基于日收益率的波动率代表相比，其值相对远离0。

本节应用QMELE方法对PGARCH模型进行拟合，采用不同频率的波动率代表的估计结果如表2所示。表2中展示了基于不同的波动率代表估计得到的参数值、残差项平方的期望和MH值。基于第4节的结论，MH值和残差项平方的期望最小时的估计最有效，因此最优的估计结果是基于RV5的估计。由表2可知，残差项平方的期望越小，MH值也越小，这与第4节的结论是一致的。同时，随着高频信息的增加，MH和残差项平方的期望也逐渐减少，这说明随着高频信息的增加基于QMELE的估计的精度随之提升。

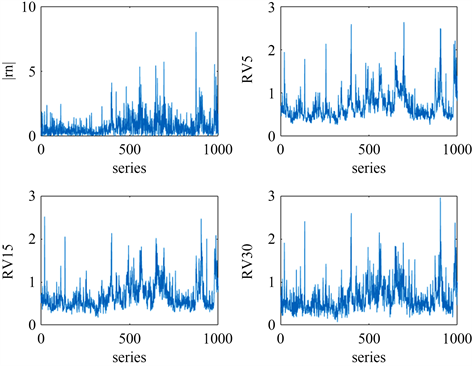
Figure 2. Time series chart of volatility proxy

图2. 波动率代表时序图

表3给出了QMELE估计的参数的渐近方差。可以看出，整合了高频信息的估计的参数的渐近方差都有所减少，尤其在PGARCH模型的幂项参数的估计的效率的增进更为明显。

那么根据表2和表3，最优的模型是基于RV5拟合得到的PGARCH模型，即：

${\sigma }_n^{\text{2}\text{.1112}}=0.0409+0.0494r_{n-1}^{\text{2}\text{.1112}}+0.8117{\sigma }_{n-1}^{\text{2}\text{.1112}}.$

Table 2. Estimation of different volatility proxy

表2. 基于不同波动率代表的估计结果

Table 3. Asymptotic variance of estimated parameter with different volatility proxy

表3. 基于不同波动率代表的参数估计的渐近方差

6. 小结

本文在传统的日频PGARCH模型的框架上，研究了日频数据和高频数据对模型参数估计的影响。特别地，文中使用了波动率代表来整合高频信息，从而研究高频数据对模型估计的影响。本文使用了拟极大指数似然估计方法(QMELE)对PGARCH模型进行拟合，并讨论了QMELE方法下的估计量的渐近性质和估计效率的判定准则，从而比较日频数据和高频数据对模型拟合的影响。而模拟研究表明，本文所使用的波动率代表在模型估计上有很好的表现，引入高频信息有助于提高PGARCH模型的估计精度。实证分析中使用了上证指数进行分析，结论支持了模拟研究中得到的结论，并发现QMELE是能明显地表现出高频数据提高了PGARCH 模型参数估计，得到的波动率也更为可靠。

基金项目

广州市科技计划项目资助(SL2022A03J00654)。