1. 引言
梅文鼎(1663~1721),字定九,号勿庵,安徽宣州人,明末清初著名天文学家和数学家。其生前研究过的许多天文学和数学问题和撰写的多本天文学和数学著作对当时和后世的影响都很大 [1] 。之所以如此,原因是其在研究天文学和数学问题的时候,不仅有对原问题的详细介绍和解读,更有对前人研究的分析和进一步深入探讨 [2] 。
1678年左右,梅文鼎写成《筹算》一书 [3] 。书中对西方传教士,特别是意大利传教士罗雅谷罗雅谷(Giacomo Rho, 1593~1638)等人 [4] [5] ,于1628年传入我国的“纳皮尔(John Napier, 1550~1617)筹算法”首次进行了介绍。书中不仅有对“纳皮尔筹算法”的详细说明,而且,还有专门针对当时国人进行数学运算习惯而进行的改造,比如把横算改为了竖算,把斜杠改为了圆弧,等等 [6] 。虽前有方中通的《数度衍》和陈訏的《句股引蒙》给出了纳皮尔筹算的介绍,但都没有对其进行深入分析,故梅文鼎此举堪称国人首次对纳皮尔筹的应用的研究与改进,是中西汇通的重要一例 [9] 。梅文鼎在《勿庵历算书目》写到:“筹算之法,盖始于《历书》时。《历引》言……其为术也,本系直筹横写,鼎此书则易之以横筹直写,乃所以适中土笔墨之宜……” [7] 初此之外,本书更有梅文鼎结合中国古代的运算特点而给出的纳皮尔筹算开带纵平方法。
对于这种方法,前人研究称这是在西方著作中没有的,就是在当时国人的有关著作中也是没有的 [6] ,因此,这是梅文鼎的一种创造 [8] [9] ,是梅文鼎的继承与发展。那么梅文鼎是怎么创造出来的呢?其有没有相关的来源呢?毕竟当时研究筹算的人很多,且中国古代很早就有开带纵平方法了。到了宋元时期我国甚至还出现了开高次方根的增乘开方法和正负开方术等 [10] 。这是个有意义的问题,尚未见有人分析。本文拟就这个问题不揣做一分析,求教各位方家。
2. 梅文鼎的纳皮尔筹算开带纵平方法
对于如何用纳皮尔筹算开带纵平方,梅文鼎在《筹算》中说:“平方者,长阔相等如棋局也。平方带纵者,直田也,长多于阔之数为之纵。平方与方纵两形,初商也。两廉一隅一廉纵四形,次商也。如次商减积不尽而有三商,则于前图之外,又加两次廉,一次隅,一次纵廉而成此图。四商以上,防此增之。凡列位作点定位,皆与开方法同。凡初商以带纵数用筹,与平方筹并列之各为法。视平方筹积数有小于实者,用其行数为初商,用其积数为方积。又视纵筹与初商同行之积数,用之为纵积。合方积纵积两数以减原实而定初商。若不及减,改而商之,及减而止。若应商十数,因无纵积,改商单九,是初商空也。则于初商之位作〇,而纪其改商之数于〇下。若次商者然(初商应是百而改九十,应千而改九百并同)。
凡次商之法,倍初商加入纵为亷法。用筹除之,视亷法筹内积数有小于余实者用为亷积。以减余实而定次商,不及减者改商之及减而止。商三次以上并同次商。凡命分之法,以所商数倍之加纵,又加隅一为命分,不尽之数为得分。凡书商数,初商五以上皆与平方法同。若四以下,则以纵之多少为进退。法以纵折半加入初商(单十以类相纵)。若满五以上者,纵进法。书于点之上两位。若纵数少虽加之而仍不满五数者,仍用常法。书于点之上一位。又初商若得单数,其亷法即为命分。凡商得单数,必在命分之上一位。” [11]
为了进一步说明上述方法,梅文鼎此后给出了若干例题。其中例题一为:“假如有直田积六十三步,但云阔不及长二步,其长阔各几何。”
这句话的意思是:假设有面积为63的长方形田地,其宽比长短2步,问长宽各实多少?
对于这个题,梅文鼎给出的求解步骤是这样的:“列位,依平方法。作点,从单位起。点在次位。合两位六十三步为实。次用平方筹与纵筹,纵二步用第二筹。平列之。各为法。视平方筹积有四九小于六三,系第七行,商作七。书于点之上二位,用进法。又视纵筹第七行积数一四,用为纵积,并方积四九,共六三,以减实恰尽。”
这段话翻译成现代文即是:
第一步:列位和作点。
把63列出来,然后在3下面点一个点。
第二步:计算初商。
由于这个题目中的纵数是2,所以选择第二筹作为纵筹。将2写到上面,作为乘数。在平方筹上寻找小于63且最接近63的平方数,即49,其对应的平方根是7,所以商是7。如图1所示。

Figure 1. Finding a quadratic equation’s root in Chou Suan (the first problem)
图1. 筹算开带纵平方第一题
第三步:计算纵积。找到平方筹行数为商的一行,计算这商和纵数2的积得到14,记为纵积。
第四步:计算次商。将初商10乘以2得200,再加上纵数2,得到廉法42。用余实除以廉法约等于4,即为次商,也称为隅法。所以得到长方形田地宽7步,长9步。
梅文鼎给出的例题二是:“假如有直田五亩,但云长多阔八十八步。其长阔各几何步。”
对于这个题,梅文鼎给出的解题步骤是:
第一步:列位和作点。
一亩是240步,所以5亩是1200步。所以1200为初商实。用点将1200分为12和00两组。由于初商是十位数,所以要在纵筹下面加一行空筹用来升位。
第二步:计算初商。
在平方筹上寻找小于12且最接近12的平方数,即9,其对应的平方根是3,所以初商是30。但是由于这个题目中的纵数88过大,所以只选择10作为初商。如图2所示。

Figure 2. Finding a quadratic equation’s root in Chou Suan (the second problem)
图2. 筹算开带纵平方第二题
第三步:计算纵积。
找到平方筹行数为商的一行,计算商和纵数88的积得到880,记为纵积。
第四步:计算余实
用平方筹计算初商10的平方得到100,并且用筹计算88与10的成绩880。用原实1200减去两者之和,得到220步,记为余实或次商实。
第五步:计算次商。
将两倍的初商,然后加纵数88,得到廉法108。然后用108三个筹,寻找108的一个10以内的倍数,使得此数小于且最接近220。发现此数是2。所以次商实为2,也是隅。
第六步:再次计算余实。
隅积为4。廉法乘以隅得到廉积216。用上次计算得到的余实220减去这个隅积和廉积之和得到0。所以得到长方形田地的宽是12步。
如果第二次得到的余实不为0,则一直循环计算第四、五、六步,直至余实为0。过程中计算得到的所有商的和即为所得。
由上面的做法中可以看到,梅文鼎在开带纵平方的过程中运用了平方筹、纵筹和空筹。平方筹是一枚较为特殊的纳皮尔筹,其从上到是1至9的平方数。纵廉是纵数对应的筹。空筹是每个位置都没有数字的筹,主要被用来升位。在计算初商的时候,梅文鼎的方法使用了平方筹来寻找最接近第一组的平方数及其开根,也就是初商。在计算纵积的时候,利用了筹算的乘法计算方法。另外,确定次商的时候利用了纳皮尔筹来寻找次商。在此三次步骤中,纳皮尔筹的作用主要是帮助求解者确定平方数和除数以及进行乘法运算,没有其他的用途。
这样,如果将这里的乘法都改为笔算,是不是就是梅文鼎的笔算开带纵平方法呢?梅文鼎在撰写《筹算》之前,还根据西方传教士的介绍写成了一本专门介绍西方笔算的书《笔算》。其中有笔算开带纵平方法。在《笔算》之初,梅文鼎还曾写道:“(筹算)其理多与笔算者相通。” [11]
3. 梅文鼎的笔算开带纵平方法
不要使用空格、制表符设置段落缩进,不要通过连续的回车符(换行符)调整段间距。在《笔算》中,梅文鼎对笔算开带纵平方的解释是:“带纵者长方形也,以方为阔,加纵数为长。其法与开方无异,但须以商得数乘纵数为纵积,并入方积以减原积。不及减者,改商之。其次商亦倍初商,加纵为廉法。但倍方而倍纵。三商以上并同。” [11]
为了说清楚上述方法,在这里梅文鼎给出的例子是:“如有长田积六百二十四步,阔不及长二步,问长阔各若干。”
该题目的意思是:如果有一个面积为624步的长方形田地,宽比长短2步,问长宽分别是多少?
梅文鼎给出的这个题的解法是:“列位,以实列右线之右,以纵二步列右线之左,对实步位列之。初商,以零六为初商实,商得二十步,自乘应减方积四百步,又以商数乘纵二步,得纵积四十步,如法列之,以减原实,仍余一百八十四步。次商,倍初商二十步作四十步,加纵二步,共四十二步为廉法,以约除余实,得商四步,即以为隅法,和廉隅总共四十六步,用乘次商四,得一百八十四,减积恰尽。得阔步二十四步,加纵二步得二十六步为长合问。”
这个过程可以表述为如下步骤:
第一步:列位和作点。
竖着列出原实(被开方数)和纵数。然后做点定位,也就是从原实最下面开始,每经过两位数点一个点。
第二步:计算初商。
把第一组数06当作初商的被开方数,得到商20步。初商自己与自己相乘得到400步。
第三步:计算余实。
然后计算初商和纵的乘积,得到40步。用原实减去初商的幂400和初商与纵40的乘积,得到184步,记为余实。
第四步:计算次商。
将初商20乘以2得40,再加上纵数2,得到廉法42。用余实除以廉法约等于4,即为次商,也称为隅法。
第五步:再次计算余实。
廉法和隅法之和为46。将其乘以次商得到184 (次商积)。用上次计算得到的余实184减去这个乘积就减完了。所以得到长方形田地的宽是24步。
如果第二次得到的余实不为0,则一直循环计算第四步和第五步,直至余实为0。过程中计算得到的所有商的和即为所得。
梅文鼎给出的计算图示如图3所示。
由此看出,在《笔算》的图示中,需要列出每一步的初商方积、初商纵积和次商积,而在筹算则不需要,这是因为纳皮尔筹的应用使得中间的运算步骤可以快速完成。然而,实质上梅文鼎在《筹算》中给出的筹算开带纵平方法与《笔算》中给出的笔算开带纵平方法一致。只不过,用算筹来算的时候,借用了算筹来计算其中的乘和除,替代了笔算中用笔来算乘和除而已。所以,梅文鼎的筹算开带纵平方法其实就是其笔算的挪移和变式。
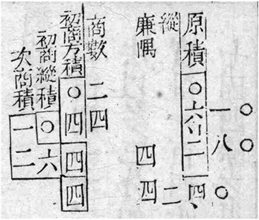
Figure 3. Finding a quadratic equation’s root in Bi Suan
图3. 笔算开带纵平方题
那么,梅文鼎的笔算开带纵平方法又是如何得到的呢?梅文鼎在《笔算》的序言中写到:“笔除原法,得数与原实相离,今所更改定者,法实与得数两两相对,算理井然,定位尤简。所谓原法者,并据《同文算指》,乃西士只书式,利西泰所授,而李水部之藻所刻也。厥后有西镜录等书,稍稍讲明定位之用。盖亦酌取中法而为之,然于古人实如法而一之旨……” [11] 由此可见,梅文鼎的笔算是在李之藻的(1565~1630,字振之,又字我存,号凉庵居士,浙江杭州人)《同文算指》的基础上写成的。
那么,他的笔算开带纵平方是不是来源于李之藻的方法呢?因为在《同文算指》中也有笔算开带纵平方的方法。
4. 李之藻的开带纵平方法
《同文算指》是明朝末年著名历算家李之藻根据意大利传教士利玛窦(Matteo Ricci, 1552~1610)对于西方数学的介绍而编译的一本重要著作。其共11卷,包括前编2卷、通编8卷,别编1卷。主要介绍了加减乘除之法与如何利用西方数学方法解决中国古代的各类问题。其中,开带纵平方法包含于第七卷中 [12] 。
在李之藻《同文算指》中笔算开带纵平方的方法是这样介绍的:“有勾股积若干,平方开之,第云勾不及股若干,用加法带除其股积余为开方,名带纵开平方法。列实,点定开位。亦列所不及为纵数于下,以首位随首点下,须于纵上空一横行,以容商除。初商若干纪格,右亦以商数并纵数,列首点下(有小数者照常退位排之)。次第呼乘以除实数,但所商数须与带纵相照。若纵数多,则减商数就之不尽之数,再倍做廉法,然倍方不倍,纵以并入带纵商之。” [12]
接下来,李之藻给出的例题是:“假设有直田积八百六十四步,阔不及长十二步,求阔几步?”
李之藻给出的解法是:“列实定位,以带纵十二随首位列之。初商二,纪格右,亦列首点下,以并带纵一,共三。乃变壹贰注三,相呼二三除六。三上捌变二。二二除四,贰上陆变二,完首段,余实二百二十四步。次倍二作四为廉法,挨退位下,亦列带纵,以廉四并纵,一其下列五,次商四,纪格右。亦注末位点下为隅法,以并隅二,下注六,乃相呼除。先呼五四除二十,进抹二,又呼四六二十四,恰尽得阔二十四步。”
这段话的意思是:
第一步:列实和注点。
即是把864列出来,并在864下面隔一位标注一个小点。然后把12也列出来,放在864的下面,靠左侧。
第二步:计算初商。
对8进行开方,得2。将这个2写在右侧,是初商。
第三步:计算余实。
然后在8的下面写一次,然后再与纵的十位1相加,得3。然后用初商2乘以这里的3,得6。然后用8减去这个6,得2。用初商2乘以纵的个位数2,得4。用上面的6减去这个4,得到2。得到余实为224。这个过程如图4所示。

Figure 4. Li Zhizao’s method of finding a quadratic equation’s root
图4. 李之藻的开带纵平方法
第四步:计算次商。
将前面初商2翻倍得到4,向右移动一位。纵12也向右移动一位。二者相加,首位为5。确定次商为4,写在右侧2的后面。同时,把这个4也写在864的个位数下面,为隅法。
第五步:再次计算余实。
用刚才得到的4加纵法12的个位数2,得到6。然后用次商4乘以56。先乘5,得到20,抹去上面的首位2。然后乘以6,得24,正好减尽上面的24。样就得到答案为24。
由上可以看出,李之藻的笔算开带纵平方法和梅文鼎的开带纵平方法除了在形式上有差别外,其步骤和过程完全一样。二者的形式差别仅仅是一个是横式一个是竖式。鉴于此,梅文鼎的笔算开带纵平方法应该来自李之藻的笔算开带纵平方法。
5. 讨论与结论
长期以来,梅文鼎在其著作《筹算》中给出的筹算开带纵平方法一直被认为是他的发明创造。经过对其方法特点的分析和方法来源的追溯,可以发现,梅文鼎筹算开带纵平方方法的思想主要有两个来源,一是明朝末年李之藻撰写的《同文算指》中的笔算开带纵平方法;二是清初时期意大利罗雅谷的《崇祯历书》中的《筹算》部分 [13] 。前者为梅文鼎方法提供了主体,而后者基于纳皮尔筹为已有方法提供了一些运算技巧。具体来讲,梅文鼎的笔算开带纵平方法的步骤、过程和算理均与李之藻在《同文算指》中给出的笔算开带纵平方法相同,二者仅仅是形式不同——梅文鼎在笔算开带纵平方过程中加入了纳皮尔筹的应用。梅文鼎的方法应当来源于李之藻的笔算开带纵平方法。梅文鼎对于开带纵平方有研究,换了一种形式,但没有实质内容的创新。不仅如此,经过梅文鼎的改造,其中的某些细节似乎是快捷了,但是,由于使用了新的工具,整个过程步骤增多了也变复杂了。这也许就是梅文鼎的筹算开带纵平方法后来没有广泛推广开来的其中一个原因。
李之藻的《同文算指》是在跟着利玛窦学习的基础上,对利玛窦的老师克拉维乌斯的《实用算术》的编译 [14] [15] [16] 。但是,对比两书,可以发现,克拉维乌斯的《实用算术》中并没有笔算开带纵平方法,只有一般的开方法 [17] 。那么,李之藻的笔算开带纵平方法是从哪里来的呢?中国古代在秦汉时期就有筹算开带纵平方法,并创造性的给出了一些相关词语,比如“实”“法”“定法”“倍法”“廉”“隅”等 [18] 。李之藻在叙述自己的开带纵平方法,也正是使用的这一套词语系统。那么,李之藻的笔算开平方法,是不是在中国古代开带纵平方法的基础上,结合当时西方传来的笔算而创造的呢?这是一个值得进一步研究的问题。如果是,则梅文鼎的创造应当算在李之藻那里。