关于图论课程教学中对染色问题的研究

Research on Coloring Problem of Graph Theory in Curriculum Teaching

摘要: 图论起源于著名的哥尼斯堡七桥问题，是离散数学的重要分支。它在计算科学、社会科学和自然科学等多个领域都有广泛应用。本文主要研究广义Petersen图的非正常点染色问题，构造满足条件的染色方式。旨在帮助学生更好地理解图论基本概念，掌握图论中的基本技巧方法，从而培养学生科学解决问题的能力。

Abstract: Graph theory, which originated from the famous Seven Bridges problem, is an important branch of discrete mathematics. It has extensive applications in many fields such as computing science, social science and natural science. In this paper, we mainly study improper coloring of generalized Petersen graphs and construct a coloring with certain requirement. It aims to help students under-stand the basic concepts and skills in graph theory, so as to guide student to develop the ability of solving scientific problems.

1. 引言

随着计算机科学的飞速发展，图论作为离散数学的一个重要分支，越来越成为各个领域研究的热点。纵观图论发展史，“四色猜想”是其中一个非常著名的问题，它与“费马猜想”，“哥德巴赫猜想”并称世界三大数学猜想。“四色猜想”的内容是：任何一张地图都可用四种颜色进行染色使得拥有共同边界的国家染以不同颜色。1976年，Appel和Haken [1] 宣称他们借助计算机历时1200个小时证明了该猜想，即“四色定理”。但关于它的理论性证明至今无人给出。在四色定理的推动下，图的染色问题受到国内外学者的高度关注，由此衍生出多种类型的染色问题，如图的点染色，边染色，点和边全染色以及列表染色等等。有兴趣的读者可从文献 [2] [3] [4] 中了解关于图染色问题的更多文献。

图的点染色问题是指用不同颜色对一个图G的顶点集进行染色，使得相邻顶点染色不同，所需的最小颜色数记为 $\chi \left(G\right)$ 。于是，四色定理可以转化为图的点染色问题，即将每个地区看作图中的一个顶点，相邻的地区之间用一条边连接，通过求证点染色问题的最小颜色数为4，从而确定地图需要4种颜色。1985年，Burr和Jacobson等人 [5] 对图的点染色做进一步推广，提出非正常点染色的概念。设 $d_1,d_2,\cdots ,d_k$ 是k个非负整数。如果图G的点集V可以被剖分成k个子集 $V_1,V_2,\cdots ,V_k$ ，使得对 $V_i$ 中的每个点v，至多 $d_i$ 个邻点与v同属于子集 $V_i$ ， $1\le i\le k$ ，则称G是非正常 $\left(d_1,d_2,\cdots ,d_k\right)$ -可染的，简称 $\left(d_1,d_2,\cdots ,d_k\right)$ -可染的。当 $d_1=d_2=\cdots =d_k=0$ 时，即为正常染色。于是，四色定理又可以表述为：每个平面图是 $\left(0\text{,0,}0\text{,0}\right)$ -可染的。近年来，图的非正常染色问题受到国内外学者的广泛关注，其研究对象为禁子圈的平面图和具有度数限制的图等，感兴趣的读者可参见文献 [6] [7] [8] [9] [10] 了解更多该方面的文献。

本文以图的非正常点染色问题为切入点，研究特殊图类的非正常2-染色问题。第二节介绍图论的基本定义和广义Petersen图的概念，第三节将给出广义Petersen图 $G\left(n,2\right)$ 的非正常2-染色结果的证明。

2. 基本概念

本文所研究的图是有限且无重边，无环的简单图，未定义的概念和符号参见文献 [11] 。

定义2.1 [11] 设 $G=\left(V,E\right)$ 是一个简单图，其中V表示点集，E表示边集。对任意的点 $u,v\in V$ ，如果 $uv\in E$ ，则称u和v邻接，u和v互称为邻点，u在图G中的所有邻点的个数称为u的度数，记为 $d\left(u\right)$ 。如果对任意的 $v\in V$ ， $d\left(v\right)=k$ ，则称G是一个k-正则图。

定义2.2 [11] 设 $u_1{u}_2{u}_3\cdots u_n$ 是图G中n个点的序列，如果对所有的 $1\le i,j\le n$ ， $u_i{u}_j\in E\left(G\right)$ 当且仅当 $u_i$ 和 $u_j$ 是连续点，则称 $P=u_1{u}_2{u}_3\cdots u_n$ 是G中的一条路。进一步地，如果 $u_1=u_n$ ，则称P是一个圈。

定义2.3 [12] 设3-正则图G的顶点集和边集分别为：

$V=\left\{u_0,u_1,u_2,\cdots ,u_{n-1};v_0,v_1,v_2\cdots ,v_{n-1}\right\}$ ， $E=\left\{u_i{u}_{i+1},u_i{v}_i,v_i{v}_{i+r}|i=0,1,\cdots ,n-1\right\}$ ，其中下标取模n， $n\ge 5$ ， $0<r<n$ ，称G为广义Petersen图，记 $G\left(n,r\right)$ 。当 $r=2$ 时， $n=5$ 和 $n=6$ 的情形见图1。

3. 广义Petesen图的非正常2-染色

定理3.1 [12] $3\le \chi \left(G\left(n,2\right)\right)\le 4$ 。

根据定理3.1，至少需要3种颜色对广义Petersen图 $G\left(n,2\right)$ 进行正常点染色。若允许某些相邻顶点染相同颜色，即非正常染色，则可达到降低色数的效果，从而在实际问题中将起到节约资源的目的。我们用数字1和2分别代表颜色，且允许每个染以颜色1 (或2)的点至多有一个邻点与其染色相同，得到如下结果。

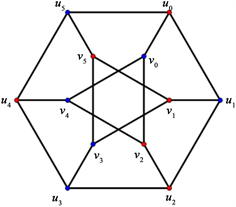
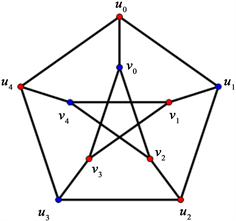(a) G(5, 2) (b) G(6, 2)

Figure 1. We use numbers 1 and 2 to denote color red and blue in the proof of Theorem 3.2, respectively

图1. 在定理3.2的证明中，红色和蓝色分别用数字1和2表示

定理3.2 $G\left(n,2\right)$ 是 $\left(1,1\right)$ -可染的。

证明：令 $G=G\left(n,2\right)$ ， $V=\left\{u_0,u_1,u_2,\cdots ,u_{n-1};v_0,v_1,v_2\cdots ,v_{n-1}\right\}$ 。我们将分别对点集 $\left\{u_0,u_1,\cdots ,u_{n-1}\right\}$ 和 $\left\{v_0,v_1,\cdots ,v_{n-1}\right\}$ 进行染色，记染色为c，其染色方式如下：首先考虑外圈 $u_0{u}_1\cdots u_{n-1}{u}_0$ ，令偶下标顶点染颜色1，奇下标顶点染颜色2，即对每一个 $i,i\in \left\{0,1,2,\cdots ,n-1\right\}$ ，如果 $i\equiv 0\left(mod2\right)$ ，则令 $c\left(u_i\right)=1$ ，如果 $i\equiv 1\left(mod2\right)$ ，则令 $c\left(u_i\right)=2$ 。

接下来考虑 $\left\{v_0,v_1,\cdots ,v_{n-1}\right\}$ ，分下述两种情形：

情形1 n为奇数。此时内部圈为 $v_0{v}_2{v}_4\cdots v_{n-3}{v}_{n-1}{v}_1{v}_3\cdots v_{n-4}{v}_{n-2}{v}_0$ 。

令 $c\left(v_0\right)=c\left(v_{n-1}\right)=2$ ， $c\left(v_{n-2}\right)=1$ 。对每一个奇数 $j,j\in \left\{1,3,5,\cdots ,n-4\right\}$ ，令 $j=2k+1$ 。如果 $k\equiv 0\left(mod2\right)$ ，则令 $c\left(v_j\right)=c\left(v_{j+1}\right)=1$ ；如果 $k\equiv 1\left(mod2\right)$ ，则令 $c\left(v_j\right)=c\left(v_{j+1}\right)=2$ ( $n=5$ 时的染色见图1)。

首先考虑 $v_i$ ， $i\in \left\{0,1,\cdots ,n-1\right\}$ ，根据 $G\left(n,2\right)$ 的定义， $v_i$ 与 $v_{i+1}$ ， $v_{i-1}$ 都不邻接。如果出现 $c\left(v_{n-4}\right)=c\left(v_{n-3}\right)=1$ ，那么由于n是奇数，按照染色规则，有 $c\left(u_{n-4}\right)=c\left(u_{n-2}\right)=2$ ，即与 $v_{n-2}$ (或 $v_{n-4}$ )染相同颜色1的邻点只有 $v_{n-4}$ (或 $v_{n-2}$ )，并且对每个 $i\ne n-2$ 且 $i\ne n-4$ ，至多一个邻点 $u_i$ 与 $v_i$ 染色相同；如果 $c\left(v_{n-4}\right)=c\left(v_{n-3}\right)=2$ ，很容易验证，对每个 $i\in \left\{0,1,\cdots ,n-1\right\}$ ，至多一个邻点 $u_i$ 与 $v_i$ 染色相同。类似地，可验证 $\left\{u_0,u_1,\cdots ,u_{n-1}\right\}$ 中的点：只有 $u_0$ 和 $u_{n-1}$ 相邻且有相同颜色1，而对于 $i\in \left\{1,2,\cdots ,n-2\right\}$ ，至多一个邻点 $v_i$ 与 $u_i$ 染色相同。

情形2 n为偶数。此时内部两个圈分别为： $v_0{v}_2{v}_4\cdots v_{n-2}{v}_0$ 和 $v_1{v}_3\cdots v_{n-1}{v}_1$ 。

首先，考虑 $\left\{v_0,v_2,\cdots ,v_{n-2}\right\}$ 。对每一个 $k,k\in \left\{0\text{,}1\text{,}\cdots ,\left(n-2\right)/2\right\}$ ，如果 $k\equiv 0\left(mod2\right)$ ，令 $c\left(v_{2k}\right)=2$ ；如果 $k\equiv 1\left(mod2\right)$ ，则令 $c\left(v_{2k}\right)=1$ 。再来考虑 $\left\{v_1,v_3,\cdots ,v_{n-1}\right\}$ 。对每一个 $k,k\in \left\{0\text{,}1\text{,}\cdots ,\left(n-2\right)/2\right\}$ ，如果 $k\equiv 0\left(mod2\right)$ ，则令 $c\left(v_{2k+1}\right)=1$ ；如果 $k\equiv 1\left(mod2\right)$ ，则令 $c\left(v_{2k+1}\right)=2$ ( $n=6$ 时的染色见图1)。

类似于情形1，对每个 $i\in \left\{0,1,\cdots ,n-1\right\}$ ，考虑 $u_i$ ，容易验证至多一个邻点 $v_i$ 与其染色相同；再考虑 $\left\{v_0,v_2,\cdots ,v_{n-2}\right\}$ ，按照染色规则， $c\left(v_0\right)=2$ ，若出现 $c\left(v_{n-2}\right)=c\left(v_0\right)=2$ ，则由于n是偶数，结合染色规则，有 $c\left(u_0\right)=c\left(u_{n-2}\right)=1$ ；最后对 $\left\{v_1,v_3,\cdots ,v_{n-1}\right\}$ 中的点分析类似。无论哪种情形，至多一个邻点与 $v_i$ 染色相同， $i\in \left\{0,1,\cdots ,n-1\right\}$ 。

定理得证。

4. 注记

注意到，定理3.2的结论是最好可能的，即不存在一种染色方式使得 $G\left(n,2\right)$ 是 $\left(1,0\right)$ -可染的。如在对 $G\left(6,2\right)$ 的染色过程中，假设所有染颜色2的点不邻接。对u₀染颜色2，则u₁和u₅需染颜色1，因为v₁和v₅相邻，所以染色不能相同。(否则，或者出现两个相邻点染颜色2，或者出现v₁和v₅都有两个邻点与其染相同颜色1，矛盾。)又由于v₃与v₅，v₁都邻接，故无论v₃染哪种颜色均产生矛盾。

本文主要研究了广义Petersen图的非正常2-染色，图论中还有许多类似问题不仅可以激发学生的学习兴趣，还可以锻炼与培养学生的逻辑思维能力和创造力。