基于改进MPC的自动驾驶轨迹跟踪控制

Automatic Driving Trajectory Tracking Control Based on Improved MPC

摘要: 在自动驾驶车辆的运行过程中，轨迹跟踪控制发挥了十分重要的作用，使得自动驾驶技术更加高效、安全。在轨迹跟踪控制中，系统通常需要根据给定的轨迹或路径，实时调整自身的状态或输出，以使系统能够沿着轨迹进行运动。为了提高轨迹跟踪控制的精度，本文将给出一个基于粒子群优化算法(PSO)的变预测时域模型预测控制(MPC)模型。利用PSO算法计算使下一时刻跟踪精度最优的预测时域大小，并将其应用到MPC控制器模型中实时改变参数，从而达到更好的跟踪效果。在MATLAB软件上与传统MPC等其他轨迹跟踪方法进行对比分析，结果表明改进后的变预测时域MPC模型在提高轨迹跟踪精度方面的表现比传统MPC控制器模型及其他轨迹跟踪方法效果更好，说明本文所提方法能够提升车辆行驶的轨迹跟踪控制精度，并具有很高的实用价值。

Abstract: In the operation process of autonomous vehicles, trajectory tracking control plays a very impor-tant role, making autonomous driving technology more efficient and safe. In trajectory tracking control, the system usually needs to adjust its own state or output in real-time according to the given trajectory or path, so that the system can move along the trajectory. In order to improve the accuracy of trajectory tracking control, this paper presents a variable prediction time domain model predictive control (MPC) model based on particle swarm optimization (PSO). PSO algorithm is used to calculate the prediction time domain size that makes the next time tracking accuracy optimal, and it is applied to the MPC controller model to change the parameters in real-time, so as to achieve a better tracking effect. Compared with other trajectory tracking methods such as traditional MPC on MATLAB software, the results show that the improved variable prediction time domain MPC model has a better performance than the traditional MPC controller model and other trajectory tracking methods in improving trajectory tracking accuracy, indicating that the proposed method can improve the trajectory tracking control accuracy of vehicle running, and has a high practical value.

1. 引言

近年来汽车智能化、网联化高速发展，自动驾驶车辆由于其可以显著减少由人为驾驶错误引起的交通事故，并有助于缓解交通拥堵的特点，受到了广泛的研究 [1] 。轨迹跟踪控制是自动驾驶车辆的关键组成部分之一，主要用于使系统(如机器人或无人驾驶车辆)沿预定的路径或轨迹移动，这种控制策略需要考虑系统的动态性能和环境因素，以确保系统能够准确、稳定地沿着预定轨迹运动。轨迹跟踪控制的准确率将会直接影响车辆的行驶轨迹，继而影响自动驾驶系统的整体性能和行车安全。如何通过技术手段提高轨迹跟踪的准确率，满足车辆在不同场景下的性能指标要求，是一个亟待解决的问题 [2] [3] [4] 。

在自动驾驶轨迹跟踪中，纯跟踪控制(Pure Pursuit, PP)、线性二次型调节器控制(Linear Quadratic Regulator, LQR)、模型预测控制(Model Predictive Control, MPC)都是常用的控制策略。纯追踪控制能够实现快速响应，但对于非线性和不确定性系统的适应性较差 [5] [6] [7] 。LQR控制能够实现最优控制，但需要建立精确的系统模型，对于不精确模型的鲁棒性较差 [8] [9] 。MPC控制则能够实现对未来的预测和优化，实现对复杂系统的高精度控制，具有良好的跟踪精度和鲁棒性，但计算复杂度较高 [10] [11] 。在四种方法中MPC控制的跟踪精度最好，但因为MPC算法的预测时域是固定的，在实际轨迹跟踪过程中面对复杂路况不具备很好的适应性，因此，本文提出了一种基于PSO的改进MPC控制策略，通过PSO算法实时优化预测时域参数，从而提高轨迹跟踪的精度和自适应性。

2. PSO-MPC算法设计

2.1. 车辆运动学模型搭建

在不考虑动力学问题的前提下，建立三自由度的自行车模型作为自动驾驶车辆的运动学模型 [12] 。

如上图1所示，以坐标系XOY为绝对坐标系，车身速度为ν m/s，车身轴距为L m，横摆角为ϕ˚，前轮转角为 ${\delta }_f$ ˚，可以得到绝对坐标系下车辆的横向、纵向速度 $\stackrel{\dot{}}{X}$ 、 $\stackrel{\dot{}}{Y}$ 分别为：

Figure 1. Kinematics model of vehicle

图1. 车辆运动学模型

$\stackrel{\dot{}}{X}=\nu \cos \phi$ (1)

$\stackrel{\dot{}}{Y}=\nu \sin \phi$ (2)

进而求得汽车角速度 $\stackrel{\dot{}}{\phi }$ ：

$\stackrel{\dot{}}{\phi }=\frac{\nu \tan {\delta }_f}{L}$ (3)

则车辆的运动学方程为：

$\left[\begin{array}{c}\stackrel{\dot{}}{X}\\ \stackrel{\dot{}}{Y}\\ \stackrel{\dot{}}{\phi }\end{array}\right]=\left[\begin{array}{c}\cos \phi \\ \sin \phi \\ \frac{\tan {\delta }_f}{L}\end{array}\right]\nu$ (4)

2.2. MPC模型搭建

模型预测控制(MPC)是一种基于数学模型的预测控制策略，通过对系统模型进行预测和优化，实现对系统的精确控制。MPC的基本思想是利用模型对未来一段时间内的系统行为进行预测，然后通过优化算法，找到最佳的控制策略，使得预测与期望目标尽可能接近，并在每个控制周期进行更新。MPC的控制过程分为预测和优化两个阶段。在预测阶段，通过数学模型预测系统的未来状态和输出。这通常基于离散时间模型，使用系统的当前状态和控制输入作为初始条件，通过模型进行模拟计算得到未来时间步长内的状态和输出。在优化阶段，根据预测结果和优化目标，通过优化算法计算出最佳的控制输入序列。优化目标通常是根据系统的性能指标设计的，例如最小化误差、保持系统稳定或最大化性能等 [12] 。

2.2.1. 预测模型

将式(3)搭建的运动学模型看作一个输入系统，输入为u，系统状态量为 $\stackrel{\dot{}}{x}$ ，则其一般形式为：

$\stackrel{\dot{}}{x}=f\left(x,u\right)$ (5)

用r表示参考量，则有：

${\stackrel{\dot{}}{x}}_r=f\left(x_r,u_r\right)$ (6)

其中， $x_r={\left[\begin{array}{ccc}{x}_r& y_r& {\phi }_r\end{array}\right]}^{\text{T}}$ ， $u_r={\left[\begin{array}{cc}{v}_r& {\delta }_r\end{array}\right]}^{\text{T}}$ 。

对式(5)在参考轨迹点处进行泰勒级数展开并忽略高阶项：

$\stackrel{\dot{}}{\tilde{x}}=f\left(x_r,u_r\right)+\frac{\partial f\left(x,u\right)}{\partial x}|\left(x-x_r\right)+\frac{\partial f\left(x,u\right)}{\partial u}|\left(u-u_r\right)$ (7)

用式(7)减去式(6)并进行离散化处理得到：

$\tilde{x}\left(k+1\right)=A\tilde{x}\left(k\right)+B\tilde{u}\left(k\right)$ (8)

2.2.2. 目标函数

在建立好车辆运动学模型后，还需要建立合适的目标函数求解系统的控制增量，通过最小化目标函数使轨迹跟踪效果更精确。本文使用的目标函数如下 [13] ：

$J\left(k\right)={\displaystyle {\sum }_{i=1}^{N_p}{\Vert \eta \left(k+i|t\right)-{\eta }_r\left(k+i|t\right)\Vert }_Q^2}+{\displaystyle {\sum }_{i=1}^{N_c-1}{\Vert \Delta U\left(k+i|t\right)\Vert }_R^2}+\rho {\epsilon }^2$ (9)

式中，N_p、N_c分别为系统的预测时域和控制时域；ε为松弛因子，ρ、Q、R为权重系数。参考文献 [13] ，将目标函数转化为二次型规划问题的一般形式：

$\underset{\Delta U}{\min }\frac{1}{2}\Delta U^{\text{T}}H\Delta U+g^{\text{T}}\Delta U$ (10)

其中， $H={\Theta }^{\text{T}}\left(I_{Np}\otimes Q\right)\Theta +I_{Np}\otimes R$ ， $g={\Theta }^{\text{T}}\left(I_{Np}\otimes Q\right)\left(E-Y_r\right)$ ， $\otimes$ 表示Kroneck 乘积，I、E、Q、R都是单位矩阵。

2.2.3. 约束条件

系统必须满足控制量和控制增量的约束，约束表达式分别为：

$\Delta U_{\min }\le \Delta U\le \Delta U_{\max }$ (11)

$U_{\min }\le A_k\Delta U+U_t\le U_{\max }$ (12)

2.3. PSO-MPC算法

在MPC算法中，预测时域是表示控制器对未来状态的预测程度的一个非常重要的参数，预测时域的大小直接决定了轨迹跟踪的效果，车速一定时，预测时域越大，能预测的距离就越远，但需要计算的数据量也就越大，因此计算速度会降低，从而产生较大误差，影响跟踪精度；同理，预测时域越小，预测距离越短，但计算速度更快，跟踪精度也会更高。车速变化时，为确保安全和准确的预测，速度越快，需要的预测时域也应更大 [14] 。

由此可见，固定的预测时域并不能达到很好的轨迹跟踪效果，只有选择使下一时刻跟踪精度最高的预测时域，才能更好地预测系统在下一时刻的输出并根据当前时刻误差及时修正系统的输入。

2.3.1. 粒子群优化算法

粒子群优化(PSO)算法最早由Barnhart博士和Kennedy博士于1995年提出，它源于对鸟群行为的研究 [15] 。作为一个迭代型优化方法，PSO算法可以通过初始化一个随机解，从而通过反复迭代找到最优值。PSO算法也具备了既能实现局部优化，又能实现全局优化的能力。

在粒子群算法中，粒子群由n个粒子组成。所有粒子会在搜索空间中以一定的速度进行飞行，这个速度受到自身和其他粒子的飞行经验的共同影响。每个粒子都有其相应的适应度值，而这个数值是由目标函数来确定的。粒子会记录已经搜索过的每个位置的适应度值，并保存其中的最优值(个体极值P_ij)和对应的位置信息X_i。除此之外，粒子们会共享信息，并标记整个群体中所有粒子在当前时刻找到的最优值(全局极值P_gj)和相应位置，这也就是所有最佳位置中的最优值 [16] [17] 。通过这种粒子群的协同行为，PSO算法能够在搜索空间中不断优化并逼近最优值。粒子们能够根据个体极值和全局极值的信息进行调整和更新，使得算法能够更好地探索和利用搜索空间中的信息。由于PSO算法具有简单而高效的特点，它在解决优化问题中得到了广泛应用。

2.3.2. PSO-MPC控制策略

由上可知，PSO算法具有很强的全局优化能力，能通过迭代找到全局最优解，而MPC算法中的预测时域需要动态调整来获得更优的跟踪精度，所以本文将两种算法进行结合，利用PSO实时计算每一步最优的预测时域大小，得出更加精确的系统控制量，提高跟踪精度。通过PSO算法优化MPC轨迹跟踪控制器的基本步骤如下：

Step 1 初始化各个参数，包括迭代次数、初始种群个数、预测时域N_p以及参考轨迹的相关参数等。

Step 2 记录当前位置的速度和位置信息，寻找预瞄距离范围内最近的参考点位置，设定一个由N个粒子组成的种群，其中的每个粒子表示为一个预测时域值：

$X_i=\left(x_1,x_2,\cdots ,x_N\right),i=1,2,\cdots ,N$ (13)

第i个粒子的“飞行”速度表示为：

$V_i=\left(v_1,v_2,\cdots ,v_N\right),i=1,2,\cdots ,N$ (14)

Step 3 计算在第i个粒子下MPC控制器输出的控制量u，并计算按此控制量输出后的实际位置与下一个最近路径点的横向误差，将横向误差作为适应度。

Step 4 利用式(15)和(16)，结合第i个粒子在第t次迭代时的速度和位置信息，计算并更新第t + 1次迭代时的最优速度和位置：

$v_{ij}\left(t+1\right)=w{v}_{ij}\left(t\right)+c_1{r}_1\left(t\right)\left[p_{ij}\left(t\right)-x_{ij}\left(t\right)\right]+c_2{r}_2\left(t\right)\left[p_{gj}\left(t\right)-x_{ij}\left(t\right)\right]$ (15)

$x_{ij}\left(t+1\right)=x_{ij}\left(t\right)+x_{ij}\left(t+1\right)$ (16)

其中，t为迭代次数，w为惯性权重系数，c₁、c₂为加速因子，P_ij(t)表示第i个粒子搜索到的个体最优值，P_gj(t)表示所有粒子在前几次迭代中得到的整体最优值。并且为了使搜索范围更加合理，设置以下的约束条件：

$\{\begin{array}{l}{v}_{ij}=v_{\max },v_{ij}\left(t\right)>v_{\max }\\ v_{ij}=v_{\min },v_{ij}\left(t\right)<v_{\min }\end{array}$ (17)

Step 5 通过不断迭代，更新粒子速度和位置并计算新位置的适应度，若新位置适应度更高，则将该粒子的位置进行更新，否则不更新。直到达到设定的迭代次数，终止迭代并输出最优适应度值对应的控制量u。

Step 6 经由MPC控制器输出，控制车辆进行轨迹跟踪并更新其位置信息。回到Step 2再进行下一个点的最优预测时域计算，经过不断迭代最终使车辆完成整个轨迹跟踪任务。

3. 仿真结果分析

为了验证文中所提出的PSO-MPC方法的有效性，基于MATLAB2022a进行计算机仿真分析。MPC控制器的时间步长设定为T = 0.1s，车身轴距L取2.9 m，预测时域N_p的取值范围定为[20, 60]，为简化计算量控制时域设为N_c = 0.5N_p。为验证本文所提方法的优势，实验同时对比了PP、LQR、传统MPC和本文改进后的MPC算法的轨迹跟踪能力，为了测试不同曲率路线下的跟踪能力，选取圆形和S型两种期望路径，仿真实验结果如下图所示。

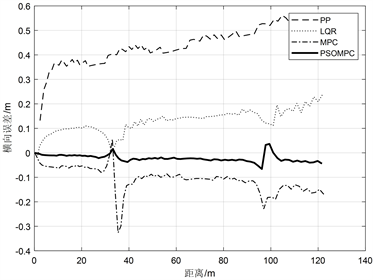(a) 横向误差 (b) 航向角误差

Figure 2. Circular desired path

图2. 圆形期望路径

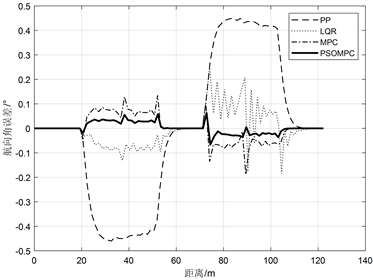(a) 横向误差 (b) 航向角误差

Figure 3. Sigmoid desired path

图3. S型期望路径

图2是期望轨迹为圆形时的跟踪效果图，对应曲率为0.05的路径，从图中可以看出，采用PP和LQR两种方法的横向误差和航向角误差都一直较大，这是由于这两种算法的适应性不强，面对不同类型的路径都需要更加精确的模型参数，而传统MPC法和本文提出的改进MPC法跟踪误差则较小，且改进后的方法明显比传统方法跟踪精度更高；图3是期望轨迹为S型时的跟踪效果图，对应曲率为0 (直线)和0.1的路径，从图中可以看出，在曲率为0的路段各方法误差精度几乎相同，但曲率变大之后，采用PP和LQR方法的误差明显增大，而改进后的MPC方法也能将各种误差控制在很好的范围内。

为了更具体的了解仿真结果，将实验数据进行归纳整理，得到表1。

Table 1. Error of different curvatures

表1. 不同曲率路径下的误差

由表1可知，曲率为0时，各方法误差都较小，但改进后的MPC方法精度更高，而且性能更加稳定，曲率为0.05和曲率为0.1的情况下，改进的MPC方法也都比其他方法的误差更小。由此可见，随着路径曲率的逐渐加大，只有改进后的方法能够始终进行较好的轨迹跟踪，且所提方法的跟踪误差相比传统MPC方法至少降低了20%，其横向误差和航向角误差的收敛速度也明显比传统MPC更快，说明改进后的MPC算法的轨迹跟踪性能是优于传统MPC和其他方法的。

由此实验结果可以得出，本文所提出的改进MPC方法是有效的，在面临不同曲率的跟踪路径时都具有良好的鲁棒性和跟踪期望轨迹的能力。

4. 结论

为了动态调整MPC模型中的预测时域参数从而降低跟踪误差，本文提出了一种基于PSO优化算法实时改变预测时域的MPC模型，在传统MPC中加入PSO优化算法，通过计算使下一时刻跟踪精度最优的预测时域大小降低预测轨迹的误差。通过与传统MPC等其他轨迹跟踪方法进行对比仿真，结果表明本文所提方法相对于传统MPC等方法能够显著提高轨迹跟踪精度，实现较好的轨迹跟踪效果。

基金项目

国家铁路智能运输系统工程技术研究中心开放课题(RITS2021KF03)。