中考路上的“勾股树”与“赵爽弦图”

The “Pythagorean Tree” and “Zhao Shuang’s String Diagram” in the Middle School Entrance Examination

摘要: 庞加莱说：“如果我们想要预见数学的将来，适当的途径是研究这门科学的历史和现状”。勾股定理的价值是非凡的，它被誉为“几何学的基石”，是欧式几何的基础定理。在日常教学中，以数学文化为入口，学习勾股定理。本文以勾股定理知识为基础，针对其中的“赵爽弦图”和“毕达哥拉斯树”两个知识点为起点，进行题目的对比分析，并给出教学建议。

Abstract: Henri Poincaré say that if we want to see the future of mathematics, the proper way is to study the history and present state of the science. The value of Pythagorean Theorem is extraordinary, which is called “the cornerstone of geometry”. It’s the fundamental theorem of Euclidean geometry. In the daily teaching, we often learn Pythagorean Theorem with the entrance of mathematical culture. In this paper, by taking the more difficult questions about Pythagorean Theorem in the secondary school entrance examination as an example, we give some teaching advices by using “Zhao Shuang’s string diagram” and “Pythagoras tree” for topic analysis.

1. 引言

随着新课程标准的落实，本着坚持目标导向、坚持问题导向、坚持创新导向的修订原则，确立了以核心素养导向的课程目标，培养“三会”的学生 [1] 。

近几年，关于“勾股定理”的中考题目已经不仅仅是注重课本知识的考察，并且在此基础上对数学知识点进行创新思维和知识迁移，这对于初中学生们的数学基础以及综合能力的要求很高。在融入数学文化的同时，让学生感受数学的思想与方法。其中“毕达哥拉斯树图”和“赵爽弦图”在每年的初中试卷中少不了它们的存在，在两个模型“外衣”下，掺杂其他知识点呈现不同的形式，这对于学生对知识点深入理解和知识点的跨越有了更大的要求，同时对教师的教学能力也有了不同之前的挑战。

从拼图到算式，通过代数表达，演绎勾股定理的证明，让学生体会数形结合思想，培养了学生的创新思维能力．从学史到运用，通过观察和求值，体会勾股定理的文化价值，增强学生运用数学知识解决问题的兴趣 [2] 。让学生和前人先生对话，体现融入数学史的探究之乐，文化之魅 [3] 。

2. 知识提出

2.1. 勾股定理的重要性

从古至今，勾股定理是一条历史悠长的数学定理。基于多元文化的角度，勾股定理是全人类共同的遗产，是数学世界上不可割离的分支。经过人类漫长的数学历史中，勾股定理是最完美的定理之一，人类已经很完美的构造出四百多种证明方法，并且它也是初等几何研究中非常重要的定理。

勾股定理的发展无一体现着同代数来解决几何问题，也正是体现着“数形结合”思想，推动了人类对数学几何更深层次的探索研究，方便我们对数学问题的解决，使数学的发展向前一大步。对于初中数学教学而言，通过融入数学史知识，渗透勾股定理的思想，可以让学生在“数形结合”方面的能力得到启蒙。在数学学习中感受人类文明的力量和中华民族对人类文明的贡献。在核心素养的教育背景下，参加数学探究活动，可以增强学生自主学习能力，合作意识，并培养尊重科学的高尚品质。

2.2. 模型解释

2.2.1. 勾股树

“勾股树”也叫“毕达哥拉斯树”，是毕达哥拉斯根据勾股定理所画出来的一个可以无限重复的图形 [4] 。又因为重复数次后的形状好似一棵树，所以被称为“勾股树”(如图1)。在时间活动中，通过构造直角三角形，用软件直接测得计算三角形三边的平方，观察两条直角边的平方和斜边平方的关系。在解题过程中，含有直角三角形和以直角三角形三边为边长向外作形状相同的图形时，可以考虑用勾股树模型解题。

Figure 1. Pythagorean tree

图1. 勾股树

基于目前数学学科与信息技术的融合，通过信息技术感受数学的学科美，领悟勾股定理蕴含的数学思想和数学内涵。教学过程中，绘制出的“勾股树”，进一步验证勾股定理，体会其中蕴含的数形结合、整体迭代、无限循环等思想。在感受数学史内里的同时，激发学生的学习兴趣、实践能力以及探索能力，提升数学核心素养。

2.2.2. 赵爽弦图

《周髀算经》中写道：“勾股各自乘，并之为玄实。开方除之，即玄”。翻译为：把勾和股分别相乘，然后把他们的积加起来，再进行开方，便可以得到弦。“赵爽弦图”最早是我国数学家赵爽对勾股定理的证明，并创制了一幅“勾股圆方图”(如图2)，用形数结合得到方法，给出了勾股定理的详细证明。赵爽的证明是极具有创新意识。既具严密性，又具直观性，为中国古代以形证数、形数统一树立了一个典范。

Figure 2. Pythagorean circle chart

图2. 勾股方圆图

“赵爽弦图”是各版教科书中“勾股定理”章节的重要内容，采用“出入相补”原理使得勾股定理的成立不证自明。定理的证明过程体现出了“数形统一”的思想，以形证数，代数和几何紧密结合互不可分，成为了几何学上的奠基石。

从“赵爽弦图”到“毕达哥拉斯树”，中外数学文化的碰撞，无一不体现数学家们的严谨的数学逻辑。数学史的发展都在向人们说明数学从来不只是枯燥的公式、定理和证明，而是一个个有温度，有思想的优秀数学家们的努力绘画出的一道道美丽的绚丽彩虹。

3. 考试题目分析

3.1. 图形面积关系

3.1.1. “勾股树”的图形面积关系

如图3，在Rt△ABC中，分别以三角形的三条边为边向外作正方形，面积分别记为S₁，S₂，S₃，若S₁ = 9，S₂ = 16，则S₃的值等于______。

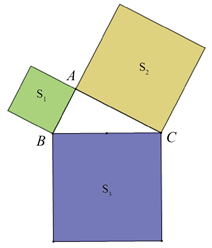
Figure 3. Pythagorean tree in relation to area

图3. 勾股树与面积关系

分析：本题目以“勾股树”为基础，以直角三角形的三边为边长向外作形状相同的图形，以及通过“勾股定理”直角三角形的三边关系，进而得出三个正方形面积之间的关系。数学的美不仅仅指代数学本身的数量关系以及空间关系，数学题的求解也能显现出其美感 [5] 。运用合适的数学模型与思想方法就能使得学系解题过程具有美感，得到有“美感”的答案，这样的解答方法也是激发学生学习数学的强大动力。

变式：如图4，在四边形ABCD中，∠ABC = ∠CDA = 90˚，分别以四边形ABCD的四条边为边长，向外作四个正方形，面积分别为S₁，S₂，S₃，S₄。若S₂ = 18，S₃ = 15，S₄ = 6，则S₁的值等于______。

Figure 4. Variant questions

图4. 变式问题

分析：本题目和上面的题目有所不同，并不是直接以直角三角形的三条边进行向外作正方形，而是一个有两个直角的四边形向外作四个正方形。根据波利亚解题，同学们以前见过它吗？或者以一种稍有不同的形式出现吗？那学生们看到这幅图想到的是什么，不能直接看出面积之间的关系，那么我们是否可以间接地和“勾股树”建立起联系？在学生的认知范围中，标准的“勾股树”是见过的，没有直角三角形就构造直角三角形，着手点是做辅助线。

3.1.2. “赵爽弦图”与图形面积的关系

(2020年河南省新乡市期中)我国汉代数学家赵爽为了证明勾股定理，创制了一副“弦图”，后人称其为“赵爽弦图”(如图5)，如图由弦图变化得到，它是由八个全等三角形的直角三角形拼接而成，记图中正方形ABCD、正方形EFGH、正方形MNKT的面积分别为S₁、S₂、S₃，若S₁ + S₂ + S₃ = 144，则S₂的值等于______。

Figure 5. Zhao Shuang’s string diagram

图5. 赵爽弦图

分析：本题目难度不大，以“赵爽弦图”为基础，来考查勾股定理的知识。要求学生熟练掌握弦图的几何特征，运用图形的变换，勾股定理、全等三角形和因式分解等知识的建构，列出其中的数量关系，通过敏锐的计算逻辑，解出此题。题目具有典型性，文化性与导向性。学生在思考题目的同时，无处不在不感受着我国数学文化的奥妙之处。利用图形中八个全等三角形和等式关系，将面积表示出来， $S_1=8x+S_3、S_2=4x+S_3$ ，带入 $S_1+S_2+S_3=144$ ，最后求出S₂。

3.2. 找规律题目

3.2.1. “勾股定理”与找规律

(2022年四川省遂宁市中考数学)“勾股树”是以正方形一边为斜边向外作直角三角形，再以该直角三角形的两直角边分别向外作正方形，重复这一过程所画出来的图形，因为重复数次后的形状好似一棵树为得名，假设如图6是第一代勾股树、第二代勾股树、第三代勾股树，按照勾股树的作图原理，则第六代勾股树中正方形的个数为。

分析：本题从“勾股树”入手，考查学生观察图形中的规律问题，解题的关键就是仔细观察图形的规律，得到图形变化的规律。学生了解“勾股树”的情况下，通过观察得到正方形的个数，考点之间的跨越，对学生数学能力有一定的要求，在感受数学中几何美的过程中锻炼探究能力，学生通过列举法，最终发现第n代勾股树正方形的个数等于 $1+2+2^2+\cdots +2^n$ 。

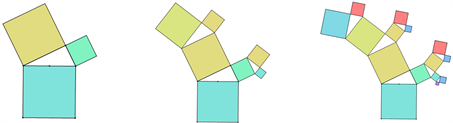
Figure 6. The law of change in the Pythagorean tree

图6. 勾股树的变化规律

3.2.2. “赵爽弦图”和找规律

如图7，已知小正方形ABCD的面积是1，把他的各边延长一倍的新正方形A₁B₁C₁D₁，把正方形A₁B₁C₁D₁边长按原法延长一倍得到正方形A₂B₂C₂D₂，以此下去……正方形A_nB_nC_nD_n的面积等于______。

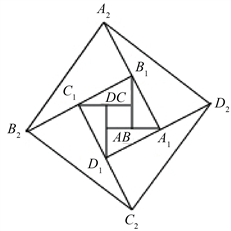
Figure 7. The law in “Zhao Shuang’s string diagram”

图7. “赵爽弦图”中的规律

分析：本题目以“赵爽弦图”为基础，通过图形边长延伸得到新的正方形，得出变化过程中的面积的变化规律，通过归纳推理得出结果。在培养学生核心素养的大环境下，本题目对于培养学生的推理能力、几何直观等能力都有了提升。无形中学习数学史，培养了科学精神。已知小正方形ABCD的面积为

1，则把它的各边延长一倍后， $\Delta \text{A}{A}_1{D}_1$ 的面积 $=\frac{1}{2}\times 2AB\times AB=A{B}^2=1$ ，新正方形 $A_1{B}_1{C}_1{D}_1$ 的面积是4 × 1

+ 1 = 5，从而正方形 $A_2{B}_2{C}_2{D}_2$ 的面积为5 × 5 = 25，以此进行下去……，则正方形 $A_n{B}_n{C}_n{D}_n$ 的面积为 $5^n$ 。

3.3. 勾股定理下的综合题目

3.3.1. “勾股树”下的综合题目

(2022年湖北省武汉市中考数学)如图8，在Rt△ABC中， $\angle ACB={90}^{°}$ ，AC > BC，分别以△ABC的三边为边向外作三个正方形ABHL，ACDE，BCFG，连接DF。过点C作AB的垂线CJ，垂足为J，分别交DF，LH于点I，K。若CI = 5，CJ = 4，则四边形AJKL的面积是______。

分析：本题是一道综合性很强的题目，考察学生对“勾股树”的熟悉程度，通过添加其他直线，考察全等三角形的判定和性质、相似三角形的判定和性质，在渗透数学史的同时，对学生的能力也是极大的挑战。

解：由题意得 $\Delta ABC\cong \Delta DFC,\Delta CJB~\Delta AJC$

∴ $\angle BCJ=\angle CAB=\angle DCI=\angle CDI$ ， $\frac{CJ}{AJ}=\frac{BJ}{CJ}$

∴ $DI=CI$ ， $CJ²=AJ\cdot BJ$

同理 $CI=IF$ ，∴ $DF=2CI=10=AB,4^2=AJ\left(10-AJ\right)$

解得 $AJ=8,BJ=2$

又∵四边形AJKL为矩形， $AL=AB=10$

$S_{矩形AJKL}=AJ·AL=8\times 10=80$

Figure 8. High School Examination Questions of Wuhan City, Hubei Province in 2022

图8. 2022年湖北省武汉市的中考题目

3.3.2. “赵爽弦图”下的综合题目

(2023年湖北省鄂州市中考题) 2002年的国际数学家大会在中国北京举行，这是21世纪全世界数学家的第一次大聚会。这次大会的会徽选定了我国古代数学家赵爽用来证明勾股定理的弦图，世人称之为“赵爽弦图”。如图9，用四个全等的直角三角形( $Rt\Delta AHB\cong Rt\Delta BEC\cong Rt\Delta CFD\cong Rt\Delta DGA$ )拼成“赵爽弦图”，得到正方形ABCD与正方形EFGH，连接AC和EG，AC与DF、EG、BH分别相交于点P、O、

Q，若BE:EQ = 3:2，则 $\frac{OP}{OE}$ 的值是______。

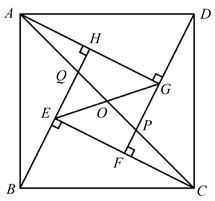
Figure 9. High School Exam Questions of Ezhou City, Hubei Province in 2023

图9. 2023年湖北省鄂州市的中考题目

分析：在“弦图”上联结一些新的线段，生成新的交点，进一步产生新的线或形，并在新元素中通

过设置限制条件，题目求 $\frac{OP}{OE}$ 的比值，发现两者之间没有直接的关系，所以需找到“中间桥梁”建立起

两者的数量关系。此题考查了正方形的性质，勾股定理，相似三角形的判定和性质，全等三角形的判定和性质，解一元二次方程以及二次根式的混合运算等知识，证明 $\Delta AHQ~\Delta CEQ$ ，求出EC的长是解题的关键。

解：设 $EC=x\left(x>0\right)$ ， $EQ=2a\left(a>0\right)$ ，则 $BE=3a$

∵ $\angle AHQ=\angle CEQ={90}^{°}$ ， $\angle AQH=\angle CQE$

∴ $\Delta AHQ~\Delta CEQ$

∴ $\frac{QH}{QE}=\frac{AH}{EC}$

∵ $Rt\Delta AHB\cong Rt\Delta BEC$

∴ $AH=BE=3a$ ， $BH=EC=x$

∴ $QH=BH-BE-EQ=x-5a$

∴ $\frac{x-5a}{2a}=\frac{3a}{x}$

整理得： $x^2-5ax-6a^2=0$

解得： $x_1=6a$ ， $x_2=-a$ (舍去)

即 $EC=BH=6a$

∴ $QH=a$ ， $EH=3a$

∴ $BC=\sqrt{B{E}^2+E{C}^2}=3\sqrt{5}a$ ， $AQ=\sqrt{A{H}^2+Q{H}^2}=\sqrt{10}a$

∴ $AC=\sqrt{2}BC=3\sqrt{10}a$

∴ $OA=\frac{1}{2}AC=\frac{3\sqrt{10}}{2}a$

∴ $OQ=OA-AQ=\frac{\sqrt{10}}{2}a$

∵四边形HEFG是正方形

∴ $\angle QEO=\angle PGO$ ， $OE=OG$

又∵ $\angle QOE=\angle POG$

∴ $\Delta QEO\cong \Delta PGO$

∴ $OP=OQ=\frac{\sqrt{10}}{2}a$

又∵ $EG=\sqrt{2}EH=3\sqrt{2}a$

∴ $OE=\frac{1}{2}EG=\frac{3\sqrt{2}}{2}a$

∴ $\frac{OP}{OE}=\frac{\frac{\sqrt{10}}{2}a}{\frac{3\sqrt{2}}{2}a}=\frac{\sqrt{5}}{3}$ 故答案为： $\frac{\sqrt{5}}{3}$

评价：不论是在“赵爽弦图”还是“毕达哥拉斯数图”模型中，基础考察是最基本的，但有其他知识的糅合，就整体提升了题目的难度，对于学生和老师都是很大的挑战。对此，给出以下教学建议，希望可以给予教学一些辅助作用。

主要观点：

1) 中考题目中，不乏以“勾股定理”为命题的相关考题，面积问题，找规律问题以及糅杂其他考点的综合类题目等，难度有易有难，教师要挖掘其中所蕴含的数学思想，拓展学生的思维，全面认识勾股定理。

2) 数学教学中，数学史的学习是以落实“立德树人”为根本任务的重要途径之一。在了解学习勾股定理的发展史的过程中，学习到数学家们严谨的科学态度，了解数学家的证明过程，从而感悟勾股定理的文化价值，树立正确的数学观。

4. 教学建议和未来研究方向

4.1. 教学建议

1) 在目前中学新课程标准中，对于提高学生的核心素养能力要求极高。平时教师在“勾股定理”的教学过程中，问题的讲授要由浅入深，由简到繁，在学习知识点巩固复习阶段，对问题进行变式，改变其中的条件或结论，或者添加其他的条件，让问题有延伸性，建立知识与知识之间的联系，提高综合素质。

2) 在勾股定理的教学中，以引入“赵爽弦图”为前提，学生画“赵爽弦图”为实践活动，可以加深学生对“赵爽弦图”的认识，提炼其显著的局部特征进行教学设计来进行勾股定理的专题教学，从识图到构图，在平时的做题过程中发现类似“赵爽弦图”的局部体征，进而解决问题。

4.2. 未来研究方向

1) “赵爽弦图”和“勾股树”是教师教学的有价值的教学资源，教师在教学过程中，带领学生挖掘其潜在的文化价值，作为德育的重要素材融入数学教学中，增加学生的活动经验，提高探究能力以及创新能力，是教师未来教学努力的方向之一。教科书中勾股定理的内容编写排版同样也是数学研究的重点方向之一，有利于教师的备课和学生的学习。

2) 目前我国的数学教育的大环境较差，虽然数学占据很重要的位置，但是却因为数学逐渐的抽象，难学，不受学生的喜爱 [6] ，在未来的数学教学研究中，将数学“简单化”，让学生爱上数学，快乐学习，爱上数学。

5. 结束语

勾股定理的教学，教师不能仅仅为了让学生学会这一个知识点，而是要让学生理解其中背后的数学思想方法，以及背后蕴含的丰富多彩的数学文化。勾股定理的教学最大的亮点是对数学文化的渗透，不是学了就行，而是在学习的过程中，要透过其定理的发现过程学习到其中的思想逻辑，这是至关重要的，知识会在后面的学习中有迁移，有挑战难度大的综合题的能力。

基金项目

国家自然科学基金项目(NO. 12361072)；2023自治区自然科学基金面上项目(2023D01A36)和青年项(2023D01B48)；2023自治区研究生精品课程项目；2022新疆师范大学校级教学团队项目；2021新疆师范大学校级一流课程项目。

NOTES

^*通讯作者。