基于谐波抑制的多频信号的仿真与实现

Simulation and Realization of Multi-Frequency Signals Based on Harmonic Suppression

摘要: 金属检测设备主要利用平衡线圈的原理，实现微弱金属信号的检测和金属杂质的剔除，广泛应用于矿业、安防、食品等行业。目前国内食品金属检测机厂商普遍使用单频信号作为发射信号，频率多为50~300 kHz，由于不同种类的金属异物检测灵敏度随频率变化不一致，且含水含盐量高的产品效应类似于铁磁性物质，因此难以实现单个频率下较好的带产品检测精度。为了弥补单频信号的不足，本文旨在实现多频发射信号的产生。首先分析选择性谐波抑制脉宽调制技术的原理，建立固定频率分量时的数学模型，通过MATLAB求解优化问题，求出输出波形导通角序列。建立Simulink电路仿真模型，通过生成的导通角，对该方法进行仿真验证，仿真表明，可以通过该方法在线圈负载上产生预期的多频信号。最后通过FPGA控制全桥D类功率放大电路驱动发射线圈，对硬件系统测试的结果显示，能够在金属探头的发射线圈上实现需要的PWM波形，实现同步多频的金属发射信号的产生。通过这样的方法产生多频信号，弥补单频金属检测机的不足。

Abstract: Metal detection equipment mainly uses the principle of balanced coil to realize the detection of weak metal signals as well as the rejection of metal impurities, which is widely used in mining, se-curity, foodstuffs and other industries. At present, domestic metal detector manufacturers of food-stuffs industry generally use a single-frequency signal as the transmitting signal, the frequency is mostly 50~300 kHz, due to the different types of metal foreign object, there will be an inconsistent trend of sensitivity with frequency change, and high water and salt content of the product generates a signal which is similar to the ferromagnetic material, so it is difficult to achieve effective distinc-tion between food and metal with single frequency. In order to make up for the deficiency of sin-gle-frequency signal, this paper aims to realize the generation of multi-frequency transmitter sig-nals. Firstly, we analyze the principle of selective harmonic suppression by pulse width modulation technology, establish the mathematical model at fixed frequency components, and solve the opti-mization problem through MATLAB to find the output waveform conduction angles sequence. A Simulink circuit simulation model is established and the method is validated by using of those conduction angles, which shows that the desired multi-frequency signal can be generated on the coil load by this method. Finally, the transmitter coil is driven by a full-bridge Class D power amplifier circuit controlled by an FPGA development board. Testing the hardware system, the results show that by this means, we can achieve the desired PWM waveforms on the transmitter coil of the metal probe to realize the generation of synchronized multi-frequency metal transmitter signals. As a re-sult, the shortcomings of single-frequency metal detectors are compensated.

1. 引言

食品金属检测系统的主要目标在于有效检测出产品中混入的金属颗粒。如何提高系统的检测精度，是近来的研究热点。在检测原理方面，主要利用平衡线圈式的传感器结构，通过分析接收线圈上的差分信号判断金属异物的有无 [1] [2] 。在检测算法方面，早期研究主要是通过分析差分信号的幅值信息来判断金属异物有无，分辨被测物和金属异物的能力较弱，后期研究结合信号的幅度和相位信息，从两个维度综合判断金属有无，大幅度提升了金属检测的带产品精度 [3] [4] 。周若臣等人分析了不同材料的金属信号随频率的变化，提出不同频率适合检测不同种类的金属 [5] 。目前国外企业如梅特勒·托利多、赛默飞世尔、安立等都已实现多频同步检测，多频检测同时利用多个频率的幅度和相位信息，当被测产品和金属异物通过线圈产生的信号的幅度和相位比较接近的时候，多频检测可以有效提高此时的带产品精度。国内多是双频切换使用，本质仍是单频检测。

SHEPWM是一种管控逆变器谐波的脉宽调制方法，广泛应用于电力电子领域，主要用来消除有害低次谐波，提升逆变器输出波形质量 [6] [7] [8] 。高丽辉等人分析了不同输出波形，如1/4周期对称、1/2周期对称和全周期不对称情况下方程组的建立，以及SHEPWM电磁激励方法在地形勘探方面的应用实例 [9] 。

基于国内现有研究的不足，提出一种产生同步多频发射信号的方法，该方法基于选择性谐波消除技术(SHEPWM)。首先根据金属材料选择需要的谐波频率，根据需要的谐波频率和分量，构建选择性谐波抑制技术的带不等式约束非线性方程组，通过优化算法，求解准确的导通角和开关时序，用这组开关时序控制开关器件的通断，从而在负载线圈上产生想要的输出波形。

2. 选择性谐波抑制算法

2.1. 选择性谐波抑制原理

在电力系统中，由于逆变器在工业领域的广泛使用，各种电子电力装置的应用会给电网带来较大的谐波污染，产生以下危害：在铁芯上产生较大的涡流损耗，增加器件发热，缩短器件使用寿命；因高频成分因集肤效应在线缆上产生更多的损耗，加速线缆老化；干扰其他设备的正常使用等 [10] [11] 。

因此使逆变器输出谐波的控制成为研究的热点，其中选择性谐波消除(SHEPWM)可以有效地消除低次谐波，将谐波能量转移到高频部分，再通过滤波技术滤除。但在食品金属检测领域中，与谐波抑制相反，是需要保留特定次谐波而不是消除特定次谐波。传统的谐波抑制算法一般用于桥式逆变电路，驱动感性负载，在金属检测应用中，可以用桥式电路来驱动发射线圈。

目前金属检测多用50~300 kHz的单频正弦波作为发射信号，选择甲乙类功率放大器驱动发射线圈，使用一个电容和线圈并联实现调谐选频的作用，因此难以实现多频输出，而使用全桥D类功率放大器，可以在实现多频输出的同时提升效率。

全桥D类功率放大电路结构如图1所示：

Figure 1. Full bridge structure class D power amplifier

图1. 全桥结构D类功率放大器

Q1，Q4导通时，电流从电源正极通过Q1流过负载，再通过Q4流到电源负极，Q2，Q3导通的时候，流过负载的电流方向相反，四个MOS管交替导通，将会在线圈负载上产生如图2所示的方波。

电感上电压表达式如下：

$U=L\frac{\text{d}i}{\text{d}t}$ (1)

由公式可知，电感上流过的电流是对电感两端电压的积分，电压水平固定时，流过电感的电流的斜率也一定，电压为+24 V时，电流以固定斜率增加，电压为−24 V时，电流以同样的斜率减少，上述电压波形对应的电感电流如图3所示。

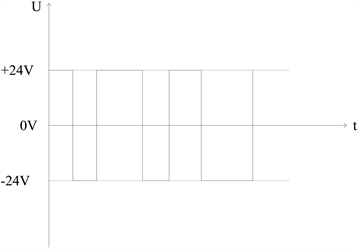
Figure 2. Voltage waveform on coil load

图2. 线圈负载上电压波形

Figure 3. Current waveform on coil load

图3. 线圈负载上电流波形

由此，可以通过控制高低电平保持的时间，也即是导通角，改变电感电流的形状，使其近似于包含特定谐波分量的电流波形，从而实现多频信号的产生。为了简化计算过程，通常设置输出波形为1/4周期对称波形，即前半个周期和后半个周期镜像对称，在同一个半周期内，前1/4周期和后1/4周期轴对称。

周期信号的傅里叶级数展开式为

$f\left(t\right)=\frac{a_0}{2}+{\displaystyle \underset{n=1}{\overset{N}{\sum }}\left(a_n\cos \left(\frac{2\pi nt}{T}\right)+b_n\sin \left(\frac{2\pi nt}{T}\right)\right)}$ (2)

当输出波形为1/4周期对称波形时，傅里叶级数中的直流分量、偶次谐波分量和奇次谐波的正弦分量都为零，从而减少了求解过程中需要的等式，极大地简化了方程和求解过程，简化后的信号傅里叶级数展开式为

$f\left(t\right)={\displaystyle \underset{p=1}{\overset{\infty }{\sum }}{c}_p\sin \left(p\omega t\right)}$ (3)

$c_p=\frac{4V_0}{p\pi }\left[1+2{\displaystyle \underset{q=1}{\overset{N}{\sum }}{\left(-1\right)}^q\cos \left(p{\alpha }_q\right)}\right]\left(p=1,3,5,7,\cdots \right)$ (4)

其中 ${\alpha }_q$ 为 $\left[0,\pi /2\right]$ 区间内的N个开关角中的第q个。结合公式(1)可推导出，电感上的电流表达式为

$I\left(t\right)={\displaystyle \underset{p=1,3,\cdots }{\overset{\infty }{\sum }}{b}_p\sin \left(p\omega t\right)}$ (5)

$b_p=-\frac{4V_0}{p^2\pi \omega L}{\displaystyle \underset{q=1}{\overset{N}{\sum }}{\left(-1\right)}^s\sin \left(p{\alpha }_q\right)}$ (6)

其中b_p即为电流信号谐波分量的幅度，当输出电压处于上升沿时，s为1，处于下降沿时，s为0。

设置p次谐波的调制比如公式(7)所示。

$m_p=\frac{V_p}{V_0}$ (7)

其中V_p为输出波形的p次谐波的幅度，V₀为驱动电压的幅度，根据以上分析，为产生特定谐波分量的输出波形，需要求解公式(8)所示带不等式约束的非线性方程：

$\underset{0\le {\alpha }_1\le {\alpha }_2\le \cdots \le {\alpha }_N\le \frac{\pi }{2},m_p}{\min }{\displaystyle \underset{p\in \Phi }{\sum }{\left(\frac{p\omega L}{V_0}{b}_p-m_p\right)}^2}$ (8)

满足公式(9)所示约束条件：

$\left|\frac{p\omega L}{V_0}{b}_p\right|\le {\phi }_p$ subject to $\left|\frac{p\omega L}{V_0}{b}_p\right|\le {\phi }_p$ $\forall p\in \Psi$ (9)

式中， $\Phi$ 为需要利用的谐波次数的集合， $\psi$ 为需要抑制的谐波次数的集合。

优化问题的求解目标为使各次谐波分量接近一定调制比时的最佳开关角序列。

2.2. 算法实现

现有单频机器的频率，根据产品的不同，多为50 kHz、150 kHz、300 kHz左右的频率，国外厂商金检机频率范围可达1 MHz。因此，在选择频率的时候，考虑各次谐波分布在50 kHz~1 MHz的范围内，谐波次数太接近会使后续分频处理复杂，难以区分相邻两个谐波分量，太远不利于充分利用中间频率的信息。本实验将FPGA频率设置为24 MHz，选择50.42 kHz作为基频，利用其1、3、7、17次谐波，具体频率如表1所示，其中最高次谐波频率为系统频率24 MHz的1/28，通过更改FPGA频率，可以很方便地更改频率组合。

Table 1. Experimental frequency selection

表1. 实验频率选择

选定频率后，一个基频信号周期内的FPGA时钟数为28乘以17，即476个FPGA时钟。

利用MATLAB产生一个谐波大小与谐波次数成反比的波形，其表达式如下：

$g\left(t\right)=\sin \left({\omega }_{1}t\right)+\frac{1}{3}\sin \left({\omega }_{3}t\right)+\frac{1}{7}\sin \left({\omega }_{7}t\right)+\frac{1}{17}\sin \left({\omega }_{17}t\right)$ (10)

波形如图4所示：

Figure 4. Desired current waveform

图4. 理想电流波形

编写Matlab程序，可以求出 $g\left(t\right)$ 在一个周期内取得极大值和极小值的时间。极值求解过程如下：先使用diff函数和sign函数，求解 $g\left(t\right)$ 的导数符号，得出一组元素为1和−1的数组，再次使用diff函数，得到元素为0，2，−2的数组，使用find函数找到元素为2和−2时的下标，此时分别对应到 $g\left(t\right)$ 的极小值和极大值。最后根据求出的下标，找到对应的取到极值点的时间，即为所求的初始值。针对图4所示波形，1/4周期内极值点大小和时间如表2所示：

Table 2. Initial value of conduction angles

表2. 导通角初始值

对应FPGA时钟数如公式(11)所示。

$N_i=\frac{t_i}{T_{FPGA}}=t_i\times f_{FPGA}$ (11)

i表示第i个导通角，所求FPGA时钟数作为选择性谐波抑制算法的初始值。

本实验一共有6个导通角，带入公式(6)，可以求得各次谐波分量大小如公式(12)所示：

$b_p=-\frac{4V_0}{p^2\pi \omega L}\left(2{\displaystyle \underset{q=1}{\overset{6}{\sum }}{\left(-1\right)}^q\sin \left(p{\alpha }_q\right)}-\sin \left(\frac{p\pi }{2}\right)\right)\left(p=1,3,5,\cdots \right)$ (12)

将公式(12)带入公式(8)，即可得出本实验的优化问题数学模型：

$\underset{0\le {\alpha }_1\le {\alpha }_2\le {\alpha }_3\le {\alpha }_4\le {\alpha }_5\le {\alpha }_6\le \frac{\pi }{2},m_p}{\min }{\displaystyle \underset{p=1,3,7,17}{\sum }{\left(\frac{8}{p\pi }{\displaystyle \underset{q=1}{\overset{6}{\sum }}{\left(-1\right)}^q\sin \left(p{\alpha }_q\right)}-\frac{4}{p\pi }\sin \left(\frac{p\pi }{2}\right)+m_p\right)}^2}$ (13)

满足公式(14)所示的约束条件：

$\left|\frac{8}{p\pi }{\displaystyle \underset{q=1}{\overset{6}{\sum }}{\left(-1\right)}^q}\sin \left(p{\alpha }_q\right)-\frac{4}{p\pi }\sin \left(\frac{p\pi }{2}\right)\right|\le {\phi }_p\forall p\in \left\{5,9,11,13,15\right\}$ (14)

特定谐波消除算法常用牛顿法求解方程组，但是对于本文中的含不等式约束问题，更适合使用内点法求解，利用Matlab的fmincon函数，可以很方便地求解该类优化问题 [12] [13] 。

2.3. 算法优化结果

优化前后的导通角如表3所示：

Table 3. Conduction angles before and after optimization

表3. 优化前后的导通角

定义谐波总谐波失真如公式(15)所示

$\text{THD}=\frac{\sqrt{{\displaystyle {\sum }_{p\in \Phi }{b}_p^2}}}{\sqrt{{\displaystyle {\sum }_{p\in \Psi }{b}_p^2}}}\times 100\%$ (15)

各次谐波分量的比例定义为 $m_p/p$ ，其中p为谐波次数。优化前后的谐波分量和总谐波失真如表4和表5所示：

Table 4. Percentage of harmonic components before and after optimization

表4. 优化前后的谐波分量占比

Table 5. THD before and after optimization

表5. 优化前后的总谐波失真

对比结果可知，优化后的总谐波失真更小，且基波和三次谐波更接近预期值。

3. Simulink电路仿真

编写Matlab代码，通过fmincon函数求解优化后的导通角，求出的导通角作为Simulink仿真电路的输入参数。为了产生控制信号的PWM波，需要将导通角与一定频率和幅度的锯齿波进行比较，使用Simulink中的Repeating Sequence模块产生锯齿波，频率和幅值可通过设置Time values和Output values改变。对于50.42 kHz基频，锯齿波的Time values设置为[0 1.9833e−5]，output value设置为[0 360]。其中1.9833e−5即为50.42 kHz对应的周期。

优化算法求解的结果是1/4周期内的导通角，因此在0到π/2之间，通过relationaloperator和logicaloperator比较各个导通角和锯齿波的值，结构如图5所示。

Figure 5. Comparison of conduction angles and sawtooth wave in 1/4 cycle

图5. 1/4周期内比较导通角与锯齿波

如图6所示，比较和逻辑判断的结果可以通过sum模块组合成输出信号，对输出求反产生两路相位相反的控制信号。

由于1/4周期对称波形的对称特征，一整个周期内的导通角都可以通过前1/4周期的导通角求出。生成的锯齿波和其中一路控制信号如图7所示，通过光标工具可以看到通过比较导通角序列和锯齿波，产生了固定导通时间的PWM控制信号。

Figure 6. Generation of two control signals

图6. 两路控制信号

Figure 7. Sawtooth wave and control signal

图7. 锯齿波和控制信号

搭建图8所示的全桥电路，以A，B两路作为控制信号，用串联的电阻和电感作为负载，直流电源选择24 V。

电阻和电感参数为0.4515欧姆和10e−6亨利，其取值为实测发射线圈参数。

最终在负载上产生的电压电流波形如图9所示，幅度为正负的电流波形的分段模拟。

结果显示，在电感负载两端产生了正负24 V的脉宽调制信号，在电感负载上产生的电流波形是对图4理想电流波形的分段拟合。因此改变导通角，最终可以实现电流波形的改变，合理设置导通角，可以产生带特定谐波分量的电流信号。

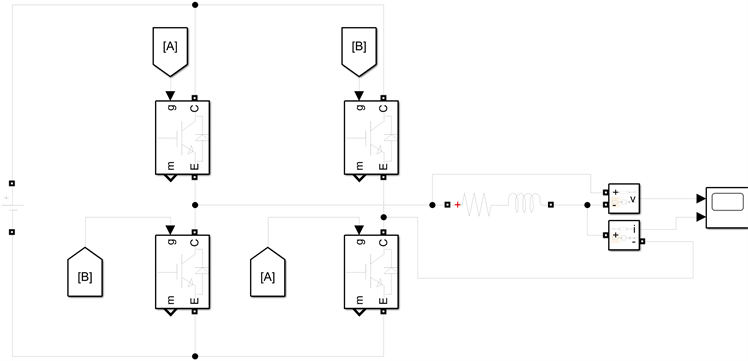
Figure 8. Simulink full-bridge circuit

图8. Simulink全桥电路

Figure 9. Simulink simulation result

图9. Simulink仿真结果

4. 硬件电路设计与实现

4.1. 硬件系统

多频信号的硬件实现需要以下几个部分：FPGA开发板、H全桥及其驱动电路、金属检测探头的发射线圈。

Matlab计算出所需要的导通角，并且转换成与24 MHz相对应的时钟数。编写FPGA代码，在固定的时钟边沿输出H全桥控制信号。所使用的FPGA系统时钟为50 MHz，因此使用PLL IP核产生24 MHz时钟。时钟配置完成后，在顶层文件实例化该模块，一个基频周期包含476个FPGA时钟，对24 MHz时钟进行计数，在每个导通角对应的时钟上升沿进行输出电平高低翻转，另一路输出对其取反，两路输出即为H桥驱动芯片的输入信号，使驱动芯片产生反相的MOS管控制信号，最终在发射线圈上产生电平为正负24 V，具有固定导通角的PWM波形。

硬件电路主要包含H全桥及其驱动电路和电源部分。由于24 V直流电源使用广泛，容易获得，因此全桥驱动电压选择24 V，使用DCDC模块，将24 V电压转换成12 V，作为驱动侧芯片供电。

H桥电路由一对PMOS和一对NMOS组成，但由于PMOS是空穴导电，导通电阻较大，开关速度不如NMOS，且可选型号少，价格偏高，因此为了减小导通时MOS管产生的功率损耗，实现更高的开关频率，常采用四个NMOS实现的全桥电路拓扑。

具体电路如图10所示。

Figure 10. Hardware schematic

图10. 硬件原理图

NMOS的导通条件是，栅极电压比源极高出至少4.5 V (以FDMS8880为例)，有的MOS管需要10~15 V才能导通。当时用4个NMOS的全桥电路时，上管导通时的源极和漏极相连，电压相等，因此源极电压也等于直流电源电压，本实验中为+24 V。为了使NMOS保持导通，NMOS的栅极电压需要比源极更高。在电路设计中，24 V已经是电路板上最高电压水平，因此使用自举电路来产生一个比直流电源更高的电压用于导通NMOS上管。

实际使用时，先导通下管，导通时下管的漏极电压为0 V，此时二极管导通，电容通过VCC电源充电，充满电后，VBOOT电压为+12 V。当下管截止，上管导通时，上管源极电压为H桥驱动电压，即+24 V。电容放电，VBOOT在驱动电压的基础上叠加电容电压，产生36 V (24 V + 12 V)的电压，此时自举电路的二极管反向截止。电容电压经过两个电阻分压之后加到上管的栅极和源极，使上管满足导通条件，从而能够持续导通。

4.2. 硬件测试结果

FPGA控制信号如图11所示。

Figure 11. Output control signal of FPGA

图11. FPGA输出控制信号

在探头的发射线圈两端测得的电压波形如图12所示，在线圈两端，产生了幅度为正负24 V，导通角可控的PWM波形，根据理论分析，该波形可以实现发射线圈上的谐波分量可控的多频电流信号。

Figure 12. Voltage waveform across the load

图12. 负载两端电压波形

5. 结论

实验基于国内现有金属检测机精度和分辨能力不够高的问题，通过对1/4周期对称波形数学表达式的分析，建立了求解包含1，3，7，17次谐波分量的输出波形的数学模型。通过Matlab求解优化问题，得到一组导通角数据。在Simulink搭建控制信号模块和全桥电路模块，对求解的导通角进行验证，仿真结果表明：可以通过给线圈施加所求导通角的PWM波，在线圈上产生谐波分量可控的电流信号，优化后的导通角产生的波形谐波失真更小，且1，3次谐波分量更靠近期望值。基于理论分析和电路仿真结果，编写了FPGA代码，产生控制信号，设计了全桥电路及其驱动电路，最终在线圈上实现了目标电压信号，从而实现金属检测机多频发射信号的产生。