次序统计量的概率性质与统计应用

The Probability Properties and Statistical Applications of Order Statistics

摘要: 基于次序统计量在数理统计(非参数统计)中的重要应用，本文对次序统计量做了相对详细的介绍。本文给出了次序统计量的概念、性质，并通过离散型总体的案例说明了次序统计量的分布不同于随机样本(总体)的分布，且不具有独立性。不同于常见的微元法而运用分部积分法对次序统计量的分布密度作出了证明，并从可视化角度给出了常见连续型总体的次序统计量分布密度的数值分析与图像拟合。最后通过常用的非参数检验方法阐释了次序统计量在统计工作中的重要应用。

Abstract: Based on the important application of order statistics in mathematical statistics (nonparametric statistics), this paper introduces order statistics in detail. The concept and properties of order sta-tistics are given, and the distribution of order statistics is different from the distribution of random samples (population) and is not independent through the case of discrete populations. Different from the common microelement method, the partial integration method is used to prove the distribution density of the order statistic, and the numerical analysis and image fitting of the distribution density of the order statistic of the common continuous population are given from the visualization perspective. Finally, the important application of order statistics in statistical work is explained by commonly used nonparametric test methods.

1. 引言

次序(顺序)统计量是数理统计学中一个非常重要的概念 [1] [2] [3] 。经典的数理统计方法其实是参数统计，是在一定的分布的情况下对未知参数进行的统计推断；而如果总体分布未知，此时非参数统计方法就显示了其重要作用。次序统计量由于其在非参数统计中的广泛应用而尤为重要。非参数统计的一个优点就是稳定性，一个重要特点就是利用样本数据的大小关系来进行研究而不依赖于总体的分布假设。而次序统计量作为排序的样本，对次序统计量的研究构成了非参数统计的基础 [4] 。

关于次序统计量的概率分布的证明，经典的概率统计教材中都是通过样本落入给定区间中的概率，通过微元法结合多项分布给出次序统计量的分布及多个次序统计量的联合分布。此经典方法对于概率统计方向的学生来讲有着简单、易懂的优点，但对于数学专业的读者来讲证明过程稍显粗糙而数学味道略淡，所以我们想能否尝试运用数学分析 [5] [6] 的工具直接对问题进行分析。具体说来，通过概率论的学习我们知道任何一个连续密度函数 $f\left(x\right)$ 都能表示成一个变上限积分 ${\displaystyle {\int }_{-\infty }^{x}f\left(x\right)\text{d}x}$ 的导数的形式。所以能否将次序统计量的分布函数表示成一个变上限积分的形式再通过微分运算得到其概率密度呢？

正文第一部分给出了次序统计量不同于普通样本的性质特点，如分布的不同及之间的不独立性，并通过具体案例加以说明。第二部分给出了次序统计量概率密度的两种推导方法，其中经典方法是基于概率统计中的多项分布结合微元法得出的，这一方法也被经典的概率统计教材所引用，而本文方法是作者基于数学分析方法的一个有益的探索，方法并不简洁甚至显冗长，但也给出了分析问题的另一种思路，为研究类似概率统计问题提供了一个可选项。第三部分通过常见分布总体的次序统计量分布密度的数值实验对结果进行了图表呈现以方便读者能更直观的理解此问题 [7] 。第四部分通过介绍次序统计量在非参数统计中的典型应用 [8] ，进一步体现了本文主题的重要性。最后一部分是对全文脉络的总结。

2. 次序统计量的性质特点

在讨论次序统计量的性质之前先简单给出其定义。设总体 的分布函数为 $F\left(x\right)$ ， $X_1,X_2,\cdots ,X_n$ 为来自总体 的一个样本，如果 $X_{\left(i\right)}\left(1\le i\le n\right)$ 的观测值总是排在样本的观测值序列 $X_1,X_2,\cdots ,X_n$ 的第 小的位置，则称 $X_{\left(i\right)}$ 为总体的第i个次序统计量 [1] [2] [3] [4] 。通过数理统计的知识我们知道样品 $X_1,X_2,\cdots ,X_n$ 之间是独立的(注意样品与样本的不同，样品指的是单个的 $X_i$ ，而样本指的是 $X_1,X_2,\cdots ,X_n$ ，也即n维随机向量 $\left(X_1,X_2,\cdots ,X_n\right)$ )，但由于次序统计量是带顺序的样本即 $X_{\left(1\right)}\le X_{\left(2\right)}\le \cdots \le X_{\left(n\right)}$ ，故次序统计量 $X_{\left(i\right)}$ 与 $X_{\left(j\right)}\left(i\ne j\right)$ 并不是独立的。由于次序统计量本身的分布不同于样本自身的分布，且次序统计量之间的不独立性，使得研究次序统计量的分布及统计量之间的关系显得更为复杂。下面两个离散情况下的例子也说明了次序统计量的分布不同于总体的分布且次序统计量之间不是独立的。

[案例1]离散总体下次序统计量 $X_{\left(i\right)}$ 与样品 $X_i\left(i=1,2,\cdots ,n\right)$ 分布不同。

设从只能取0，1的贝努利总体 $X~B\left(1,1/2\right)$ 中抽取容量为3的样本 $x_1,x_2,x_3$ ，则显然根据样本的性质知 $X_i~B\left(1,1/2\right)$ ，但第 次序统计量 $X_{\left(i\right)}$ 的分布却未必，事实上可以得到样本的各个取值的如下表1的概率：

Table 1. The value of the sample and order statistics

表1. 样本及次序统计量的取值情况

于是 $P\left(X_{\left(1\right)}=0\right)=7/8$ ， $P\left(X_{\left(1\right)}=1\right)=1/8$ ； $P\left(X_{\left(2\right)}=0\right)=1/2$ ， $P\left(X_{\left(2\right)}=1\right)=1/2$ ； $P\left(X_{\left(3\right)}=0\right)=1/8$ ， $P\left(X_{\left(3\right)}=1\right)=7/8$ ，可以将次序统计量 $X_{\left(i\right)}$ 的分布列表如下表2：

Table 2. The probability distribution of each order statistic

表2. 各次序统计量的概率分布

可见 $X_{\left(1\right)}~B\left(1,1/8\right)$ ； $X_{\left(2\right)}~B\left(1,1/2\right)$ ； $X_{\left(3\right)}~B\left(1,7/8\right)$ ，显然与样品 $X_i$ 的分布不同。同时，可得 $X_{\left(1\right)}$ 与 $X_{\left(2\right)}$ 的联合分布如下面列联表3所示：

Table 3. Joined contingency table distribution of X ( 1 ) and X ( 2 )

表3. $X_{\left(1\right)}$ 与 $X_{\left(2\right)}$ 的联合列联表分布

易见 $P\left(X_{\left(1\right)}=0,X_{\left(2\right)}=0\right)=\frac{1}{2}\ne P\left(X_{\left(1\right)}=0\right)P\left(X_{\left(2\right)}=0\right)=\frac{7}{8}\times \frac{1}{2}$ ，显然 $X_{\left(i\right)}$ 与 $X_{\left(j\right)}\left(i\ne j\right)$ 之间不独立。本

案例是离散总体的，当然对于连续总体来说次序统计量 $X_{\left(i\right)}$ 的分布与样品 $X_i$ 的分布也是不同的。下面先给出连续总体下次序统计量的密度函数公式。

3. 连续总体下次序统计量的概率密度函数及证明

3.1. 次序统计量密度函数公式及常规证明

设总体X是连续型随机变量，分布函数为 $F\left(x\right)$ ，密度函数为 $f\left(x\right)$ ， $\left(X_1,X_2,\cdots ,X_n\right)$ 为取自X的一个样本， $\left(X_{\left(1\right)},X_{\left(2\right)},\cdots ,X_{\left(n\right)}\right)$ 为次序统计量，则次序统计量 $X_{\left(i\right)}\left(i=1,2,\cdots ,n\right)$ 的密度函数为：

$f_i\left(y\right)=\frac{n!}{\left(i-1\right)!1!\left(n-i\right)!}{\left(F\left(y\right)\right)}^{i-1}{\left(1-F\left(y\right)\right)}^{n-i}f\left(y\right)$ (1)

一般的数理统计教材中提供的证明方法 [1] [2] [3] 是一种基于多项分布背景下的微元法处理方式。即将实数轴 $\left(-\infty ,+\infty \right)$ 划分为三个区间 $\left(-\infty ,y\right]\cup \left(y,y+dy\right]\cup \left(y+dy,+\infty \right)$ ，若 $x_{\left(i\right)}$ 落入区间 $\left(y,y+dy\right]$ ，按照次序统计量的定义知区间 $\left(y,y+dy\right]$ 内有1个样品落入，区间 $\left(-\infty ,y\right]$ 内有 $i-1$ 个 ${X^{\prime }}_{i}s$ 落入，余下的 $n-i$ 个样品落入区间 $\left(y+dy,+\infty \right)$ ，由多项分布(这里是三项)的构造，可以确定概率

$\begin{array}{l}P\left(y\le x_{\left(i\right)}\le y+dy\right)\\ =\frac{n!}{\left(i-1\right)!1!\left(n-i\right)!}{\left(F\left(y\right)\right)}^{i-1}\left(F\left(y+dy\right)-F\left(y\right)\right){\left(1-F\left(y+dy\right)\right)}^{n-i}\\ =\frac{n!}{\left(i-1\right)!1!\left(n-i\right)!}{\left(F\left(y\right)\right)}^{i-1}\left(f\left(y\right)dy\right){\left(1-F\left(y+dy\right)\right)}^{n-i}\end{array}$

从而 $x_{\left(i\right)}$ 的概率密度函数为

$f_i\left(y\right)=\underset{dy\to 0}{\lim }\frac{P\left(y\le x_{\left(i\right)}\le y+dy\right)}{dy}=\frac{n!}{\left(i-1\right)!1!\left(n-i\right)!}{\left(F\left(y\right)\right)}^{i-1}{\left(1-F\left(y\right)\right)}^{n-i}f(\; y\; )$

可见其概率思想即将 $x_{\left(i\right)}$ 先框定在一个微小的区间内，然后将这个随机事件等价转化为 $\left(-\infty ,y\right]$ 内有 $i-1$ 个样品落入， $\left(y,y+dy\right]$ 内有1个样品落入(即 $x_{\left(i\right)}$ )，则 $\left(y+dy,+\infty \right)$ 内有 $n-i$ 个样品落入，从而将概率 $P\left(y\le x_{\left(i\right)}\le y+dy\right)$ 转化为一个三项分布，再根据F与f的关系通过微元法解决问题。

3.2. 数学分析证明方法探讨

上面的经典方法固然简洁，但是基于数学的魅力，我们能否通过纯粹的数学分析的方法来思考这个问题？虽然方法不一定简洁明了，但是作为对此问题的不同的思考角度，我们相信若能实现此数学推导，仍然是有益的尝试。为此先给出如下的引理1，并将此一般结论在数理统计的背景下加以具体应用。

引理设实数 $a\in \left[0,1\right]$ ， $n\in Z^{+}$ ， $i=0,1,2,\cdots ,n$ ，则

$I={\displaystyle {\int }_0^a{x}^{i-1}{\left(1-x\right)}^{n-i}\text{d}x}={\displaystyle {\sum }_{k=i}^n\frac{\left(i-1\right)!\left(n-i\right)!}{n!}{C}_n^i{a}^k{\left(1-a\right)}^{n-k}}$ (2)

证明利用分部积分法

$\begin{array}{c}I={\displaystyle {\int }_0^a{x}^{i-1}{\left(1-x\right)}^{n-i}\text{d}x}=\frac{1}{i}{\displaystyle {\int }_0^a{\left(1-x\right)}^{n-i}\text{d}{x}^i}\\ =\frac{1}{i}{a}^i{\left(1-a\right)}^{n-i}+\frac{n-i}{i}{\displaystyle {\int }_0^a{x}^i{\left(1-x\right)}^{n-i-1}\text{d}x}\\ =\frac{1}{i}{a}^i{\left(1-a\right)}^{n-i}+\frac{n-i}{i\left(i+1\right)}{a}^{i+1}{\left(1-a\right)}^{n-i+1}+\frac{\left(n-i\right)\left(n-i-1\right)}{i\left(i+1\right)}{\displaystyle {\int }_0^a{x}^{i+1}{\left(1-x\right)}^{n-r-2}\text{d}x}\end{array}$

同样的积分方法可以依次进行下去有：

$\begin{array}{c}I=\frac{1}{i}{a}^i{\left(1-a\right)}^{n-i}+\frac{n-i}{i\left(i+1\right)}{a}^{i+1}{\left(1-a\right)}^{n-i+1}+\frac{\left(n-i\right)\left(n-i-1\right)}{i\left(i+1\right)\left(i+2\right)}{a}^{i+2}{\left(1-a\right)}^{n-i-2}\\ +\cdot \cdot \cdot +\frac{\left(n-i\right)\left(n-i-1\right)\cdot \cdot \cdot 3\cdot 2}{i\left(i+1\right)\cdot \cdot \cdot \left(n-2\right)}{\displaystyle {\int }_0^a{x}^{n-2}\left(1-x\right)\text{d}x}+\frac{\left(n-i\right)!}{i\left(i+1\right)\cdot \cdot \cdot \left(n-1\right)n}{a}^n\\ ={\displaystyle {\sum }_{k=i}^n\frac{\left(i-1\right)!\left(n-i\right)!}{k!\left(n-k\right)!}{a}^k{\left(1-a\right)}^{n-k}}={\displaystyle {\sum }_{k=i}^n\frac{\left(i-1\right)!\left(n-i\right)!}{n!}{C}_n^i{a}^k{\left(1-a\right)}^{n-k}}\end{array}$

定理 设连续总体X的分布函数为 $F\left(x\right)$ ，密度函数为 $f\left(x\right)$ ， $X_1,X_2,\cdots ,X_n$ 为从总体中提取的容量为n的样本，那么第i个次序统计量 $X_{\left(i\right)}\left(i=1,2,\cdots ,n\right)$ 的概率密度函数为

$f_i\left(x\right)=\frac{n!}{\left(i-1\right)!\left(n-i\right)!}{\left(F\left(x\right)\right)}^{i-1}{\left(1-F\left(x\right)\right)}^{n-i}f(\; x\; )$

证明由概率分布函数的定义易见 $X_{\left(i\right)}$ 的分布函数为

$F_i\left(x\right)=P\left(X_{\left(i\right)}\le x\right)={\displaystyle {\sum }_{k=i}^n\left(\begin{array}{c}n\\ k\end{array}\right)F^k\left(x\right){\left(1-F\left(x\right)\right)}^{n-k}}$ (3)

由引理1，可得 $X_{\left(i\right)}$ 的分布函数为 $F_i\left(x\right)=\frac{n!}{\left(i-1\right)!\left(n-i\right)!}{\displaystyle {\int }_0^{F\left(x\right)}{x}^{i-1}{\left(1-x\right)}^{n-i}\text{d}x}$ ，密度函数

$\begin{array}{c}{f}_i\left(x\right)={F^{\prime }}_i\left(x\right)=\frac{\text{d}}{\text{d}x}\left\{\frac{n!}{\left(i-1\right)!\left(n-i\right)!}{\displaystyle {\int }_0^{F\left(x\right)}{x}^{i-1}{\left(1-x\right)}^{n-i}\text{d}x}\right\}\\ =\frac{n!}{\left(i-1\right)!\left(n-i\right)!}{\left(F\left(x\right)\right)}^{i-1}{\left(1-F\left(x\right)\right)}^{n-i}f(\; x\; )\end{array}$

4. 连续总体下次序统计量密度函数的数值实验

[案例2] 设总体 $X~f\left(x\right)=\{\begin{array}{cc}\frac{1}{10}{\text{e}}^{-\frac{1}{10}x}& x>0\\ 0& x\le 0\end{array}$， $\left(X_1,X_2,X_3,X_4\right)$ 为来自X的容量为4的样本， $\left(X_{\left(1\right)},X_{\left(2\right)},X_{\left(3\right)},X_{\left(4\right)}\right)$ 为相应的次序统计量，可通过描绘 $X_{\left(i\right)}$ 的密度函数曲线以反映次序统计量的分布规律。事实上， $F\left(x\right)=1-{\text{e}}^{-\frac{1}{10}x},x>0$ ，故 $X_{\left(i\right)}$ 的密度函数为：

$f_1\left(x\right)=\frac{4!}{\left(1-1\right)!\left(4-1\right)!}{\left(1-{\text{e}}^{-\frac{1}{10}x}\right)}^{1-1}{\left({\text{e}}^{-\frac{1}{10}x}\right)}^{4-1}\frac{1}{10}{\text{e}}^{-\frac{1}{10}x}=0.4{\text{e}}^{-0.4x}~\exp (\; 0.4\; )$

$f_2\left(x\right)=\frac{4!}{\left(2-1\right)!\left(4-2\right)!}{\left(1-{\text{e}}^{-\frac{1}{10}x}\right)}^{2-1}{\left({\text{e}}^{-\frac{1}{10}x}\right)}^{4-2}\frac{1}{10}{\text{e}}^{-\frac{1}{10}x}=1.2\left({\text{e}}^{-0.3x}-{\text{e}}^{-0.4x}\right)$

$f_3\left(x\right)=\frac{4!}{\left(3-1\right)!\left(4-3\right)!}{\left(1-{\text{e}}^{-\frac{1}{10}x}\right)}^{3-1}{\left({\text{e}}^{-\frac{1}{10}x}\right)}^{4-3}\frac{1}{10}{\text{e}}^{-\frac{1}{10}x}=1.2{\text{e}}^{-0.2x}{\left(1-{\text{e}}^{-0.1x}\right)}^2$

$f_4\left(x\right)=\frac{4!}{\left(4-1\right)!\left(4-4\right)!}{\left(1-{\text{e}}^{-\frac{1}{10}x}\right)}^{4-1}{\left({\text{e}}^{-\frac{1}{10}x}\right)}^{4-4}\frac{1}{10}{\text{e}}^{-\frac{1}{10}x}=0.4{\text{e}}^{-0.1x}{\left(1-{\text{e}}^{-0.1x}\right)}^3$

它们各自的图像用Matlab [7] 绘制如图1~5所示，图6为多分布共图展示。

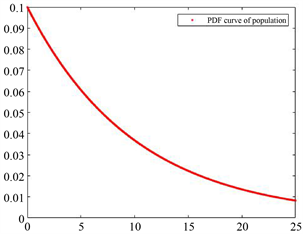
Figure 1. PDF curve of population Exp(0.1)

图1. 总体Exp(0.1)的概率密度函数曲线

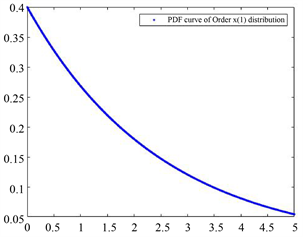
Figure 2. PDF curve of $X_{(\; 1\; )}$

图2. $X_{\left(1\right)}$ 的概率密度函数曲线

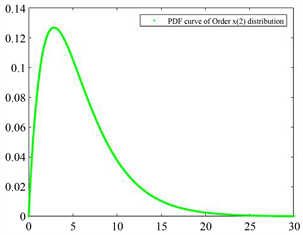
Figure 3. PDF curve of $X_{(\; 2\; )}$

图3. $X_{\left(2\right)}$ 的概率密度函数曲线

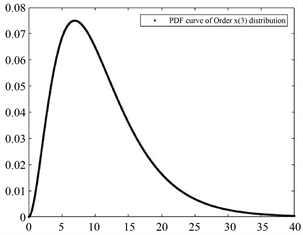
Figure 4. PDF curve of $X_{(\; 3\; )}$

图4. $X_{\left(3\right)}$ 的概率密度函数曲线

Figure 5. PDF curve of $X_{(\; 4\; )}$

图5. $X_{\left(4\right)}$ 的概率密度函数曲线

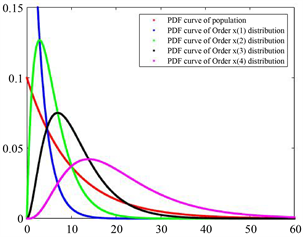
Figure 6. Mixed curve of the distributions

图6. 各分布的混合曲线

在画 $X_i$ (或总体X)及 $X_{\left(i\right)}\left(i=1,2,3,4\right)$ 分布图时考虑到它们的数学期望分别为：

$EX={\displaystyle {\int }_0^{+\infty }xf\left(x\right)\text{d}x}=10$ ； $E{X}_{\left(1\right)}={\displaystyle {\int }_0^{+\infty }x{f}_1\left(x\right)\text{d}x}=2.50$

$E{X}_{\left(2\right)}={\displaystyle {\int }_0^{+\infty }x{f}_2\left(x\right)\text{d}x}\approx 5.83$ ； $E{X}_{\left(3\right)}={\displaystyle {\int }_0^{+\infty }x{f}_3\left(x\right)\text{d}x}\approx 10.83$

$E{X}_{\left(4\right)}={\displaystyle {\int }_0^{+\infty }x{f}_4\left(x\right)\text{d}x}\approx 20.83$

如下表4所示：

Table 4. The expected value of each order statistics

表4. 各次序统计量的数学期望

参照它们的数学期望值可以选取适当的坐标区间画出合适的图像。图6中的图像与它们单独的图像形状上的不同是由于坐标轴(主要是横轴)的取值范围的不同导致的。 $X_i$ 与 $X_{\left(1\right)}$ 的分布虽然有形状上的类似，毕竟都是指数分布，但无论密度函数的众数、极大值还是尾部厚度都有明显的不同， $X_{\left(3\right)}$ 与 $X_{\left(4\right)}$ 的区别类似，而且 $X_{\left(2\right)}$ 的密度曲线的凹凸区间与 $X_{\left(3\right)}$ 、 $X_{\left(4\right)}$ 有明显的不同， $X_{\left(2\right)}$ 在众数之前是凹的，之后是凸的，而 $X_{\left(3\right)}$ 、 $X_{\left(4\right)}$ 呈现出先凸后凹再凸的形态。可见，次序统计量 $\left(X_{\left(1\right)},X_{\left(2\right)},\cdots ,X_{\left(n\right)}\right)$ 与随机样本 $\left(X_1,X_2,\cdots ,X_n\right)$ 具有明显不同的分布，本质原因是排序之后的次序统计量一定程度上削弱了随机性。

5. 次序统计量在非参数统计中的重要应用 [4]

次序统计量之所以重要是在于其在非参数统计中的广泛应用，特别是由次序统计量衍生出的秩的概念。在样本 $\left(X_1,X_2,\cdots ,X_n\right)$ 中，如果 $X_i$ 是第 $R_i$ 个最小的，即 $X_i=X_{\left(R_i\right)}$ ，则称 $X_i$ 的秩为 $R_i$ ，这样可以得到样本的一个统计量 $R=\left(R_1,R_2,\cdots ,R_n\right)$ ，所有由样本的秩所产生的统计量统称为秩统计量。为说明秩统计量在非参数检验中的应用，我们选取非参数检验中常用的两独立样本的Mann-Whitney U检验与检验样本相关性的Spearman秩相关分析加以说明。Mann-Whitney U检验可以用来检验两样本所属的总体是否具有相同分布，是利用样本数据的秩而不是样本特定值来检验结果的统计显著性。Spearman秩相关分析不是单纯给出了两成对数据的相关系数，而是通过相对严格的假设检验对两样本是否正相关给出了统计检验。

5.1. Mann-Whitney U检验 [4]

将两组样本数据 $X_1,X_2,\cdots ,X_m$ 和 $Y_1,Y_2,\cdots ,Y_n$ 混合并按升序排列，得到每个数据的秩 $R_i$ ；然后分别对样本 $X_1,X_2,\cdots ,X_m$ 和 $Y_1,Y_2,\cdots ,Y_n$ 的秩求平均，得到两个平均秩 $W_{X/m}$ 和 $W_{Y/n}$ ，然后根据这两个平均秩构造Mann-Whitney U统计量，基于本文的阐述重点，这两种非参检验的检验统计量的形式具体可参见 [4] ，这里通过对如下案例的分析来对这两种检验加以说明。

[案例3] [8] 现有铅作业工人与非铅作业工人的血铅值(μg/100g)，如下表5所示，其中组1表示非铅作业工人的血铅值，组2表示铅作业工人的血铅值，试检验两组工人的血铅值有无显著差别(α = 0.05)。

1) 参数检验：如果运用经典的两独立样本t检验，则需要正态性前提。分别对两个组的样本数据通过正态性检验可以得到如下正态QQ图(图7、图8)。

Table 5. Data lists of blood lead values for two groups of workers

表5. 两组工人血铅值的数据列表

Figure 7. Normal QQ plot of Group 1

图7. 组1的正态QQ图

Figure 8. Normal QQ plot of Group 2

图8. 组2的正态QQ图

发现两个组的样本数据的观测值与期望正态值基本在一条直线上，可以直观上认为正态性满足，通过配对样本t检验，得t检验统计量结果为−6.4，检验的p值为0.001，高度显著，认为两组工人的血铅值显著不同。参数方法的优点在于统计量计算简单，检验精度较高，但需总体的正态性加持，很多时候这也是一个很大的弊端，而基于次序统计量及衍生出来的秩统计量的Mann-Whitney U检验则无需此假设，可直接检验。

2) 非参数检验：不需要做正态性检验，直接对两组样本值做Mann-Whitney U检验，得如下检验结果(图9、图10)：

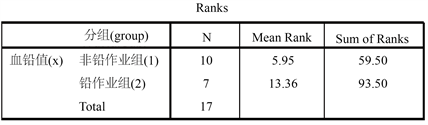
Figure 9. Mean rank and sum of ranks for two blood lead value groups

图9. 两组血铅值混合后的平均秩与秩和

Figure 10. Test result

图10. 检验结果

基于Mann-Whitney U检验的检验统计量的公式 [4] ，本案例中的统计量值为4.500，检验的p值为0.001，仍然高度显著，说明铅作业工人与非铅作业工人的血铅值有显著差异，事实上组2的平均值27.8远超组1的平均值9.9且差异显著。

5.2. Spearman秩相关检验 [4]

[案例4]某高校某班17人某门课程的期中考试成绩X与期末考试成绩Y的观测值如下表6所示：

Table 6. Observations of Midterm score X and Endterm score Y

表6. 期中成绩X与期末成绩Y的观测值

从中断定期末考试成绩与期中考试成绩是否正相关？

[分析]为了检验：H₀：X和Y不相关；H₁：X和Y正相关，对数据进行秩排序可以得到如下的表格，秩排序规则为 $X_i=X_{\left(R_i\right)}$ ， $Y_i=Y_{\left(Q_i\right)}$ $\left(i=1,2,\cdots ,17\right)$，

构造检验统计量 $S={\displaystyle {\sum }_{i=1}^{17}{\left(R_i-Q_i\right)}^2}=272$ ，计算Spearman相关系数 $r_s=1-\frac{6S}{n\left(n^2-1\right)}=0.667$ (这里

$n=17$ )，在 $\alpha =0.01$ 的显著性水平下，查Spearman秩相关系数检验的临界值表得 $c_{0.01}=0.566$ ，由 $r_s>c_{0.01}$ ，拒绝原假设，认为是正相关的。由SPSS软件得出的Pearson相关系数与Spearman秩相关系数及显著性检验结果如下(图11、图12)：

Figure 11. Pearson correlations test

图11. Pearson相关检验

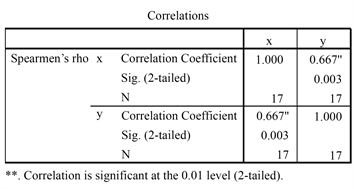
Figure 12. Spearman rank correlations test

图12. Spearman秩相关检验

可见，Pearson相关系数 $r=\frac{{\displaystyle {\sum }_{i=1}^n\left(X_i-\bar{X}\right)\left(Y_i-\bar{Y}\right)}}{{\displaystyle {\sum }_{i=1}^n{\left(X_i-\bar{X}\right)}^2}{\displaystyle {\sum }_{i=1}^n{\left(Y_i-\bar{Y}\right)}^2}}=0.546$ ，在α = 0.05下是显著的，p-value =

0.023 < 0.05；Spearman相关系数r_s = 0.667，在α = 0.01下是显著的(也称高度显著)，p-value = 0.003 < 0.01，也即在本例中Spearman秩相关检验比常见的Pearson相关检验具有更小的犯一类错误的概率。

6. 总结与展望

次序统计量由于其在非参数统计中的大量应用而显得尤为重要。本文从次序统计量的概念与性质出发，通过具体案例展示了离散总体下次序统计量的分布与随机样本分布不同，且丧失了样本原有的独立性。理论推导部分运用数学分析方法给出了次序统计量密度函数的另一种证明方法，该方法虽然不比微元法轻巧，但作为数学分析方法在概率中的一个应用，不失为一种有益的尝试。基于已经得到的连续总体下次序统计量密度函数公式，通过数值实验说明了次序统计量与样本的分布明显不同。最后通过次序统计量引出的秩统计量的概念，结合Mann-Whitney U检验和Spearman秩相关检验说明了次序统计量在非参数检验中的重要应用。篇幅所限，其他大量的非参数应用本文不赘述。次序统计量、秩统计量及各种非参数检验场合下检验统计量的构造问题，显著性的非参数检验问题可以作为本文的后续研究内容，作为经典的参数统计推断的补充，这显然是一项非常有价值的研究课题。

基金项目

上海理工大学教师发展研究项目(CFTD2023YB40)。

NOTES

^*通讯作者。