1. 引言
随着工业技术的发展和需求的不断增加,对机械设备性能的要求也日益提高。在众多机械传动元件中,轴承作为支撑和传递机械装置运动的重要组成部分,其性能对设备的工作效率和使用寿命影响巨大。然而,在高速、高负载工况下,传统的轴承常常面临着润滑不足、摩擦损失大等问题,限制了机械设备的性能和可靠性。
为了解决这些问题,自润滑向心关节轴承作为一种新型的轴承结构应运而生。其相较于传统轴承无需外部润滑,摩擦损失较小,运行更为稳定,因而在机械工业、铁路运输、建筑工程等领域 [1] [2] [3] 应用广阔,得到了学者们的广泛关注。
随着工程数学与计算力学的发展进步,有限元分析技术被广泛应用于轴承力学性能的研究。向定汉等 [4] 利用Ansys有限元分析软件对关节轴承结构进行优化,以提升轴承的耐磨性;李科委等 [5] 利用有限元法分析具有自润滑特性且承受径向载荷的轴承的受力和形变方面情况;胡宝根等 [6] 利用Ansys Workbench对额定静载荷下自润滑关节轴承的应力和变形进行了深入分析,以探究其性能特征;霍亚军等 [7] 在研究中采用Abaqus软件及软件上进行定制开发的用户自定义程序,对轴承结构进行了稳定性、物理过程耦合和热力学效应的综合分析;基于有限元法,段宏瑜等 [8] 分析了承载径向力对轴承的各构成部分的影响;林志埙 [9] 对可能导致关节轴承变形或磨损的径向外力或荷载的情况进行了分析;吴连平等 [10] 利用Abaqus软件通过调整工艺参数来改善制造过程设计进行了虚拟正交试验,通过有限数量的试验点对多个因素进行组合和分析,找到了最优的参数组合。
本文分析了自润滑向心关节轴承的静力学和摩擦特性。通过建立静力学模型探讨了自润滑向心关节轴承在不同工况下的受力分布情况,以及其承载能力和稳定性。并考虑其摩擦与热力的耦合效应,分析了摩擦产生的热量对轴承性能的影响。本文的研究,旨在为自润滑向心关节轴承的设计和优化提供理论支持,进一步提升机械设备的性能和可靠性。
2. 关节轴承的基本结构参数
自润滑向心关节轴承在工作过程中承受的主要负荷为径向载荷,也可承载一定的轴向载荷,以REBDW-12型自润滑向心关节轴承为研究对象,其结构如图1所示,该关节轴承由内圈和外圈组成,内外圈组成一个滑动摩擦副。该关节轴承的主要结构参数如表1所示。

 (a) 三维结构示意图 (b) 尺寸参数示意图
(a) 三维结构示意图 (b) 尺寸参数示意图
Figure 1. Diagram of self-lubricating spherical bearings
图1. 自润滑关节轴承示意图

Table 1. Main paremeters of joint bearings
表1. 关节轴承主要参数
其中内圈所用的材料为Gcr15,外圈为碳素钢,表2列出了材料的密度、杨氏模量及泊松比等参数。

Table 2. Relevant parameters of self-lubricating radial spherical plain bearing materials
表2. 自润滑向心关节轴承材料相关参数
3. 基于Workbench的自润滑关节轴承静力学分析
3.1. 建立有限元仿真模型
在AnsysWorkbench软件的静态结构模块中导入简化后的关节轴承模型,根据表1中的数据,设置各零部件的材料参数。然后划分模型网格。通过在静态结构分析软件中添加轴承座零件,并在模型中定义相应的材料属性,可以准确地模拟关节轴承在实际工况下的响应。轴承座选用45钢作为材料,其弹性模量为206 Gpa,密度为7 850 kg/m3,泊松比为0.24。考虑到加载变形会影响初始接触状态,即选择六面体主导网格的方法划分轴承座,内外圈则选择四面体网格划分,单元尺寸分别设置为1.5 mm和1 mm。该有限元模型包含100,896个单元,结构示意如图2所示。

Figure 2. Finite element model of self-lubricating spherical bearing and bearing housing
图2. 自润滑关节轴承及轴承座有限元模型
3.2. 设定边界约束及载荷
取图3所示的两种工况进行静态结构分析:
1) 工况一:在正常工作状态下,在轴承内圈内球面施加方向为z轴负方向,大小为185.6 KN的纯径向载荷。
2) 工况二:在正常工作状态下,除工况一条件之外,在内圈圆环端面上施加大小为45 kN的载荷,方向为y轴正方向。
两种工况的载荷以及边界条件如下:
A——Bearing Load,内圈内球面施加185.6 kN的径向载荷,方向为z轴负方向;
B——Fixed Support,固定约束;
C——Bearing Load,内圈一端面施加45 kN的轴向载荷,方向为y轴正方向;
D——Displacement,位移约束,限制轴向加载面相应的轴承座端面在x方向的位移。

 (a) 工况1 (b) 工况2
(a) 工况1 (b) 工况2
Figure 3. Self-lubricating spherical bearing loads and boundary conditions
图3. 自润滑关节轴承载荷及边界条件
3.3. 静力学结果分析
工况一下自润滑向心关节轴承的von Mises应力分布情况如图4所示。根据图中显示结果:内圈的最大等效应力为2925.4 MPa,位于内表面上,这是因为该表面承受了径向载荷;外圈的最大等效应力为2380.1 MPa,出现在外表面的外侧边缘处,此处的应力远大于其他外圈部分,发生了明显的明显应力集中;接触应力的最大值为2183.5 MPa,主要分布在外圈内表面与内圈外表面接触挤压的区域。

 (a) 外圈等效应力 (b) 内圈等效应力
(a) 外圈等效应力 (b) 内圈等效应力 (c) 接触应力
(c) 接触应力
Figure 4. Equivalent stress distribution diagram under working condition 1
图4. 工况1下等效应力分布图
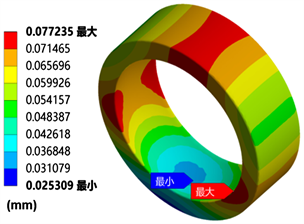
工况一下的内、外圈均发生不同程度的变形,位移如图5所示。
 (a) 外圈位移 (b) 内圈位移
(a) 外圈位移 (b) 内圈位移
Figure 5. Displacement distribution map under working condition 1
图5. 工况1下位移分布图
根据图5显示的结果,最大位移为0.2609 mm,发生在内圈内表面边缘处。这表明内圈在承受径向载荷时的行为特征。由于内圈的宽度大于外圈,导致内圈在承受载荷时承受了更大的应力。特别是在承受径向载荷时,内圈的两侧会产生应力集中现象,导致两侧产生较大变形;外圈最大变形出现在内表面两侧边缘处,最大值为0.077235 mm。
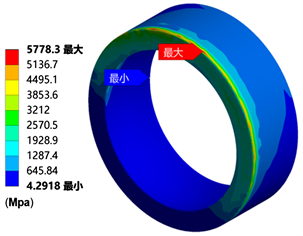
下图6、图7所示为工况二下静力学分析结果。由图6可知:外圈最大von Mises应力位于轴向加载对应侧端面的外侧边缘处,数值为5778.3 MPa。这一结果表明,轴向加载使得内外圈发生了挤压效应,导致外圈在轴向加载的另一侧同时承受了较大的径向挤压和轴向挤压。在承受径向和轴向联合载荷的情况下,外圈的von Mises应力值大于仅进行径向加载的情况;内圈的最大von Mises应力为2319.7 MPa;接触应力朝着轴向加载的另一侧偏移,且最大值明显大于仅径向加载时,为3698.9 MPa。
由图7可知工况2下关节轴承内、外圈最大位移为0.39358 mm,出现在内圈远离轴向加载一侧端面的边缘处;外圈最大变形出现在内表面轴向加载的另侧边缘处,最大值为0.082774 mm。
 (a) 外圈等效应力 (b) 内圈等效应力
(a) 外圈等效应力 (b) 内圈等效应力 (c) 接触应力
(c) 接触应力
Figure 6. Equivalent stress distribution diagram under working condition 1
图6. 工况2下等效应力分布图

 (a) 外圈位移(b) 内圈位移
(a) 外圈位移(b) 内圈位移
Figure 7. Displacement distribution map under working condition 1
图7. 工况2下位移分布图
4. 自润滑关节轴承热力耦合分析
利用Ansys Workbench的瞬态动力学模块对关节轴承进行热力耦合分析,得到轴承摩擦生热的温度场云图。
4.1. 有限元模型设定
在关节轴承转动过程中,内、外圈之间会发生摩擦并产生热量,当温度升高到一定程度时会对轴承的寿命和性能造成影响。现进行关节轴承旋转时的摩擦热分析,考虑到热力耦合分析计算复杂,提出以下假设来简化有限元模型:
1) 内、外圈接触面的摩擦因数μ都为0.12,且恒定不变;
2) 不考虑材料磨损,且摩擦、挤压所做的功全部转化成热量;
3) 热膨胀系数α、热导率λ、比热C为常数,不随温度的变化而变化;
4) 不考虑热辐射以及其余表面与环境之间的热对流,将摩擦面传热系数设定为1.8 × 104 (W/m2∙℃)。
4.2. 有限元建模
将加载板作为刚体零件引入模型中,以模拟实际工作环境下的应力情况。内、外圈材料参数见表1。约束上端面在x、y轴的位移,限制关节轴承内圈内球面除绕y轴旋转之外的所有自由度。内圈外球面与外圈内球面之间的摩擦因数为0.12。
在分析设置中加入两个载荷步骤:
1) 保持内圈静止,逐渐施加载荷至185.6 kN;
2) 恒定载荷185.6 kN,内圈以不同转速绕y轴进行轴向旋转。
设置系统初始温度为22℃,对关节轴承内圈转数为24 rad/min、48 rad/min、72 rad/min、96 rad/min、120 rad/min时分别进行热力耦合分析。下图8为分析时的加载与约束模型
A——Bearing Load,外圈外表面施加185.6 kN的径向载荷,方向为z轴负方向;
B——Displacement,位移约束;
C——Convection,对流;
D——Connect auxiliary load,连接副载荷,对内圈施加旋转速度。
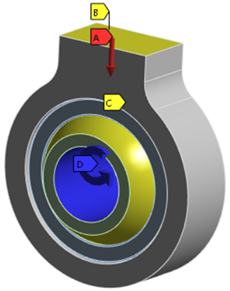
Figure 8. Loads and boundary conditions
图8. 载荷及边界条件
4.3. 计算结果及分析
下图9、图10分别为自润滑关节轴承在不同转速下外圈、内圈的温度随时间的变化云图。
综上分析可知,外圈接触面中心的温度较高,这是由于越靠近接触面的中心位置,接触应力越大,从而导致更多的摩擦热生成,因此外圈的温度场分布从接触面中心向边缘逐渐降低。而内圈最高温区位于靠近内外圈接触边缘的地方。
5. 结论
本文利用Ansys Workbench分析计算了REBDW-12型自润滑关节轴承的应力、位移以及力–摩擦耦合温度场,得出以下结论:
1) 仅加载径向载荷时,外圈最大von Mises应力表现在外表面的外侧边缘处,内圈最大von Mises应力表现在载荷的加载表面上,最大接触压力主要分布在外圈内球面与内圈外球面的挤压区域。同时施加径向和轴向载荷时,内、外圈的最大等效应力和最大接触应力均高于仅施加径向载荷时。
2) 在关节轴承承受径向载荷并转动时,外、内圈之间的摩擦现象显著增加并产生摩擦热。随着内圈转速增加,摩擦产热快于轴承导热,导致轴承持续升温。外圈温度较高的区域与内圈温度较高的区域对应分布在接触面上。因此,应尽量避免轴承在内圈高转速下长时间工作,防止温升过高降低关节轴承的使用性能。另外,可通过设计合适的轴承构造来提高润滑性能,降低磨擦因数,进而降低磨擦热的生成。
3) 在实际工况中关节轴承还存在内圈摆动、倾斜受力等影响,因此可进一步考虑更多工况下的有限元分析,并将本文应用的分析计算方法扩展到结构分析和优化设计中。