1. 引言
求解热传导方程初边值问题的精确解,通常用分离变量法 [1] 。但是寻求精确解往往比较困难,因此,一般是寻求逼近精确解的数值解。文献 [2] 中关于如何用差分法来求解热传导方程初值以及初边值问题的数值解有详细介绍;文献 [3] [4] 是用Lagrange插值来求解非线性热传导方程数值解;文献 [5] [6] [7] 则是用谱方法来逼近求解一些热传导方程:文献 [5] 用Cheyshev谱配置法来求解热传导方程初边值问题;文献 [6] 用Laguerre拟谱方法来求解半无界非线性热传导方程问题;文献 [7] 用Legendre-Hermite混合谱方法数值求解无穷带状区域上的各向异性线性热传导方程。最近,有作者用含参数的三次样条插值来求解常微分方程 [8] [9] [10] ,但是还未曾有人将其用来求解偏微分方程,本文用含参数三次样条插值求线性热传导方程的数值解,通过适当选取参数提高数值误差精度。
2. 算法格式
2.1. Legendre-Gauss-Lobatto节点
n次Legendre多项式的定义如下:
选取
为多项式
的
个互异的零点,也即为Legendre-Gauss-Lobatto节点。
以Legendre-Gauss-Lobatto节点为配置点来构造含参数三次样条函数,然后用含参数的三次样条函数来逼近求解热传导方程初边值问题。
2.2. 含参数的三次样条函数
使用变量变换
,
,将求解区间
映射到区间
。并将区间
划分成n个小的子区间
。
一般来说,对函数
在插值节点
处进行插值形成的含参三次样条插值函数的好坏程度,即
逼近函数
的好坏程度,取决于参数
的适当选取以及当参数
时三次样条函数在区间
上的改变程度。
该样条函数
在区间
上满足以下的微分方程 [9] :
(1)
公式(1)是一类二阶常系数非齐次常微分方程。它的通解与相对应的齐次方程的通解以及它自己本身的一个特解有关。
显然,与公式(1)相对应的齐次方程的通解如下:
同时,有公式(1)的一个特解如下:
令
,再由插值条件:
,则可以得到公式(1)的通解,如下:
(2)
对公式(2)两端进行求导并令
,则有:
当
时,有
,
。类似上面步骤,可以得到:
由
在节点
处的连续性条件,可以得到:
(3)
其中:
2.3. 热传导方程算法格式
带Dirichlet边界条件热传导方程:
(4)
用三次样条函数
来逼近方程(4)的解,由(4)式可得:
其中:
。
考虑
前面的系数,有:
(5)
记
为
,并将(5)代入(3)中得到:
(6)
由(4)中给出的边界条件,处理得:
,则(6)可写成如下形式:
(7)
(8)
(9)
由(4)的初值条件:
,得:
。
为方便处理,记:
;
;
有了以上的符号说明,则(7)~(9)可以写成如下形式:
(10)
3. 数值例子
用式(10)求解式(4),在时间方向用步长为
的Crank-Nicolson格式离散,则:
用如下定义的
-范数来度量误差:
其中
为三次样条误差,
为一阶导数误差,
为二阶导数误差。下面给出一些数值结果,以验证该格式的有效性和高精度。
例1:考虑以下微分方程:
(11)
现有微分方程(11)的一个精确解:
。
当三次样条参数
变化时,图1给出
-范数
的常用对数
及不同
之间的关系,
其中
取值为0.001。可以看到数值误差随N的增加而快速衰减,当参数
取0.1时,可以获得较好的数
值结果。在图2中,给出
时数值误差常用对数
随N的增加及不同的
的变化情况。可以
看到,随着
的减小,数值误差随N的增加而快速衰减,这表明计算格式的高精度和稳定性。

Figure 1.
图1.
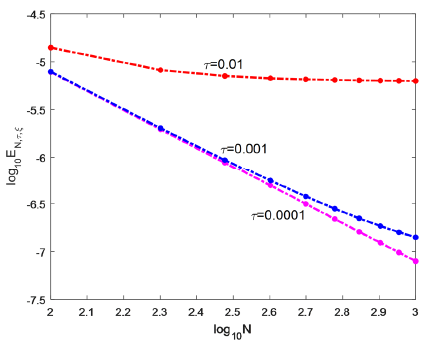
Figure 2.
图2.
图3给出了一阶导数误差,图4给出二阶导数误差,其中
。可以看到,用三次样条函数来逼近求解方程(11)时,其一阶导数和二阶导数也分别收敛于精确解的一阶导数与二阶导数,并且具有很好的收敛速度。
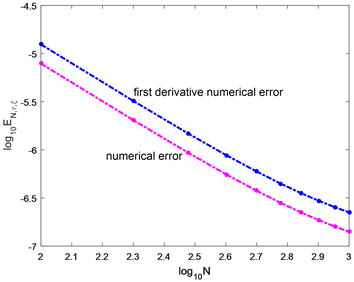
Figure 3.
图3.
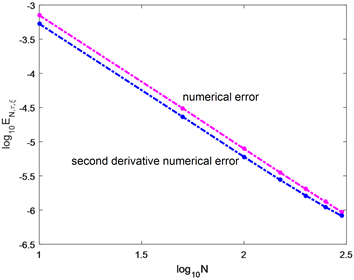
Figure 4.
图4.
例2:考虑以下微分方程:
(12)
现有微分方程(12)的一个精确解:
。
图5给出
取值为0.0001时
与
之间的关系。可以看到数值误差随N的增加而快速衰减,而当参数
取0.6时,获得较好的数值结果。在图6中,T取值为1:随着
的减小,数值误差随N的增加而快速衰减,这表明计算格式的高精度和稳定性。图7、图8分别给出了一阶导数误差、二阶导数误差,其中
。同样可以看到,用三次样条函数来逼近求解方程(12)时,其一阶导数和二阶导数也分别收敛于精确解的一阶导数与二阶导数,并且具有很好的收敛速度。
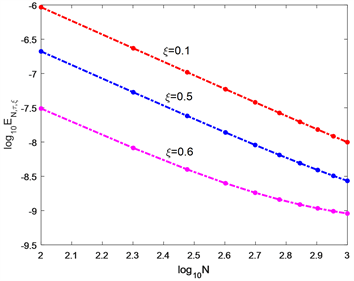
Figure 5.
图5.
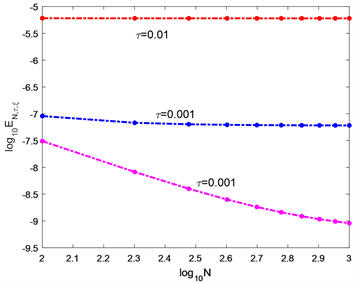
Figure 6.
图6.

Figure 7.
图7.

Figure 8.
图8.
4. 结论
本文利用含参数的三次样条插值函数来逼近热传导方程精确解。以Legendre-Gauss-Lobatto节点为配置点,先构造含参数的三次样条插值来对空间进行离散,再在时间方向上应用步长为
的Crank-Nicolson格式,然后得到带Dirichlet边界条件热传导方程的数值解。由数值实验得到的结果来看,提出的算法不仅具有一定的有效性和高精度,并且对于精确解的导数也有很好的逼近效果。
致谢
首先,我要感谢基金项目:国家自然科学基金项目(11371123)!最后,对于师姐柴果、师妹马亚楠以及实验室的同学们表示感谢!谢谢你们对我的支持和帮助!
基金项目
国家自然科学基金项目(11371123)。